AP Inter 1st Year Physics Study Material Chapter 2 Units and Measurements

Andhra Pradesh BIEAP AP Inter 1st Year Physics Study Material 2nd Lesson Units and Measurements Textbook Questions and Answers.

AP Inter 1st Year Physics Study Material 2nd Lesson Units and Measurements

Very Short Answer Questions

Question 1.
Distinguish between accuracy and precision. [A.P. Mar. 16, 15; T.S. Mar. 15, 13]
Answer:
Accuracy

1. The accuracy of measurement of any physical quantity made by any measuring instrument is a measure of how close the measured value is to the true value of the quantity.
2. The accuracy depends on errors.

Precision

1. The precision of the measuring instrument denotes upto what limit (or) resolution the quantity can be measured with the given instrument.
2. The precision does not depend on errors.

Question 2.
What are the different types of errors that can occur in a measurement?
Answer:
Mainly there are three types of errors.

1. Systematic errors
2. Random errors
3. Gross errors.

Question 3.
How can systematic errors be minimised or eliminated ? [Mar. 14]
Answer:
Systematic errors can be minimised by improving experimental techniques, selecting better instruments and removing personal bias as far as possible. For a given set up, these errors may be estimated to a certain extent and the necessary corrections may be applied to the readings.

Question 4.
Illustrate how the result of a measurement is to be reported indicating the error involved. [T.S., A.P. – Mar. 17]
Answer:
To measure any physical quantity, we compare it with a standard (unit) of that quantity. No measurement is perfect as the errors involved in the process cannot be removed completely. Hence inspite of our best efforts, the measured value is always some what different from its actual value (or) true value.

Question 5.
What are significant figures and what do they represent when reporting the result of a measurement ? [Mar. 13]
Answer:
The digits of a number that are definitely known plus one more digit that is estimated are called significant digits (or) significant figures.
Example : Time period of a simple pendulum is 1.62, the digits 1 and 6 are reliable while the digit 2 is uncertain. The measured value has three significant figures.

Question 6.
Distinguish between fundamental units and derived units. [T.S. – Mar. 16]
Answer:

1. Units of fundamental quantities are called fundamental units. Fundamental units can neither derived from one another, nor can they be resolved into other units.
2. Units of derived quantities are called derived units.

Question 7.
Why do we have different units for the same physical quantity ?
Answer:
We have different systems like C.G.S system, M.K.S system, F.P.S system and S.l system. Hence we have different physical units for the same physical quantity.

Question 8.
What is dimensional analysis ?
Answer:
Dimensional analysis is the representation of derived physical quantities in terms of units of fundamental quantities.

With the help of dimensional analysis to check the correctness of the equation, convert one system of units into other system and derive certain equations relating physical quantities.

Question 9.
How many orders of magnitude greater is the radius of the atom as compared to that of the nucleus ?
Answer:
Size of atomic nucleus = 10^-14 m
Size of atom = 10^-10 m
Hence size of atom is 1CT4 m greater the size of the nucleus.

Question 10.
Express unified atomic mass unit in kg.
Answer:
1 unified atomic mass unit = \(\frac{1}{12}\) of the mass of carbon – 12 atom.
1 a.m.u = 1.66 × 10^-27 kg

Short Answer Questions

Question 1.
The vernier scale of an instrument has 50 divisions which coincide with 49 main scale divisions. If each main scale division is 0.5 mm, then using this instrument what would be the minimum inaccuracy in the measurement of distance ?
Answer:
Value of each main scale division = 0.5 mm
No. of vernier scale divisions = 50
In vernier callipers, L.C = \(\frac{S}{N}=\frac{\text { Value of one main scale division }}{\text { No. of vernier scale divisions }}\)
L.C. = \(\frac{0.5}{50}\) = 0.01 m.m
The minimum inaccuracy in the measurement of distance is 0.01 m.m. (Or)
Value of 1 MSD = 0.5 m.m
NV.S.D = (N – 1) M.S.D
50 V.S.D – 49 M.S.D
1 V.S.D = \(\) M.S.D. = \(\frac{49}{50}\) × 0.5
L.C = 1 M.S.D – 1 V.S.D
(0.5 – \(\frac{49}{50}\) × 0.5) = (1 – \(\frac{49}{50}\))0.5 = \(\frac{1}{50}\) × 0.5
L.C. = 0.01 m.
∴ Minimum inaccuracy in the measurement of distance is 0.01 m.m.

Question 2.
In a system of units, the unit of force is 100 IM. unit of length is 10 m and the unit of time is 100s. What is the unit of mass in this system ?
Answer:
Force (F) = 100 N; Length (L) = 10 m; Time (T) = 100 s F = ma
mass (m) = \(\frac{F}{a}=\frac{F}{L T^{-2}}\); m = \(\frac{\mathrm{FT}^2}{\mathrm{~L}}=\frac{100 \times(100)^2}{10}\) = 10⁵ kg

Question 3.
The distance of a galaxy from Earth is of the order of 10²⁵ m. Calculate the order of magnitude of the time taken by light to reach us from the galaxy.
Answer:
Distance of galaxy from earth = 10²⁵ m
Velocity of light (C) = 3 × 10⁸ m/s
Time taken by the light (t) = \(\frac{\text { Distance of galaxy from earth }}{\text { velocity of light }}\)
t = \(\frac{\mathrm{d}}{\mathrm{c}}\) ⇒ t = \(\frac{10^{25}}{3 \times 10^8}\) = 0.33 × 10¹⁷ s ⇒ t = 3.3 × 10¹⁶ sec.

Question 4.
The Earth-Moon distance is about 60 Earth radius. What will be the approximate diameter of the Earth as seen from the Moon?
Answer:
Distance between Earth-Moon = 60 R
Radius of the earth = R
r = 60R = 60 × 6400 × 10³ (R = 6400km)
θ = 1 sec = \(\frac{1}{60}\) Min = \(\frac{1}{60 \times 60}\) degree ⇒ θ = \(\frac{1}{60 \times 60} \times \frac{\pi}{180}\) radian
Then r = \(\frac{l}{\theta}\) ⇒ l = rθ ⇒ l = 60 × 6400 × 10³ × \(\frac{1}{60 \times 60} \times \frac{\pi}{180}\)
l = 11.16 × 10³ km ⇒ Diamter (l) = 11.16 × 10³ km

Question 5.
Three measurements of the time for 20 oscillations of a pendulum give t₁ = 39.6 s, t₂ = 39.9 s and t₃ = 39.5 s. What is the precision in the measurements? What is the accuracy of the measurements?
Answer:
No. of oscillations = 20
t₁ = 39.6 sec, t₂ = 39.9 sec, t₃ = 39.5 sec
Mean value = \(\frac{t_1+t_2+t_3}{3}=\frac{39.6+39.9+39.5}{3}=\frac{119}{3}\) = 39.66
Mean value = 39.7 sec;
Precision = 0.1 sec.
Accuracy is the closeness of measured value with true value.
Hence 39.6 s is accuracy.

Question 6.
1 calorie = 4.2J where 1J = 1 kg m²s². Suppose we employ a system of units in which the unit of mass is \(\hat{a}\) kg, the unit of length is \(\hat{a}\) m and the unit of time is \(\tilde{a}\) s, show that a calorie has a magnitude 4.2 \(\hat{\mathrm{a}}^{-1} \hat{a}^{-2} \tilde{\mathrm{a}}^{-2}\) in the new system.
Answer:
1 Calorie = 4. 2J ⇒ 1 J = 1 kg m² s^-2
1 calorie = 4.2 kg m² s^-2
In new system, 1 calorie = 4.2 \(\hat{a} \hat{a}^2 \hat{a}^{-2}\)

Question 7.
A new unit of length is chosen so that the speed of light in vacuum is 1 ms-2. If light takes 8 min and 20 $ to cover this distance, what is the distance between the Sun and Earth in terms of the new unit ?
Answer:
V = Speed of light in vacuum = 1 m/s
Time taken (t) = 8 min 20 sec = 500 sec
Distance between the sun and earth (d) = \(\frac{\mathrm{V}}{\mathrm{t}}\) ⇒ d = \(\frac{1}{500}\) = 0.002 m.

Question 8.
A student measures the thickness of a human hair using a microscope of magnification 100. He makes 20 observations and finds that the average thickness (as viewed in the microscope) is 3.5 mm. What is the estimate of the thickness of hair ?
Answer:
Magnification of microscope = M = 100
Observed thickness = 3.5 m.m
Magnification (M) = \(\frac{\text { Observed thickness }}{\text { Real thickness }}\) ⇒ 100 = \(\frac{3.5}{\text { Real thickness }(t)}\) ⇒ t = \(\frac{3.5}{100}\) = 0.035 m.m.

Question 9.
A physical quantity X is related to four measureable quantities a, b, c and d as follows. X = a² b³ c^5/2d^-2
The percentage error in the measurement of a, b, c and d are 1%, 2%, 3% and 4% respectively. What is the percentage error in X ?
Answer:
X = a² b³ c^5/2d^-2
\(\frac{\Delta \mathrm{a}}{\mathrm{a}}\) × 100 = 1%, \(\frac{\Delta \mathrm{b}}{\mathrm{b}}\) × 100 = 2%, \(\frac{\Delta \mathrm{c}}{\mathrm{c}}\) × 100 = 3%, \(\frac{\Delta \mathrm{d}}{\mathrm{d}}\) × 100 = 4%
Percentage error in X is
(\(\frac{\Delta \mathrm{X}}{\mathrm{X}}\)) × 100 = 2(\(\frac{\Delta \mathrm{a}}{\mathrm{a}}\) × 100) + 3(\(\frac{\Delta \mathrm{b}}{\mathrm{b}}\) × 100) + \(\frac{5}{2}\) (\(\frac{\Delta \mathrm{b}}{\mathrm{b}}\) × 100) + 2 \(\frac{\Delta \mathrm{d}}{\mathrm{d}}\) × 100
= 2 × 1 + 3 × 2 + \(\frac{5}{2}\) × 3 + 2 × 4 = 2 + 6 + \(\frac{15}{2}\) + 8
⇒ (\(\frac{\Delta \mathrm{X}}{\mathrm{X}}\) 100 = 23.5 %

Question 10.
The velocity of a body is given by v = At² + Bt + C. If v and t are expressed in SI what are the units of A, B and C ?
Answer:
Given V = At² + Bt + C
According to principle of homogeneity,

1. V = At² ⇒ A =\(\frac{\mathrm{V}}{\mathrm{t}^2}=\frac{\mathrm{LT}^{-1}}{\mathrm{~T}^2}\) = [LT^-3] ⇒ A = ms^-3
2. V = Bt ⇒ B = \(\frac{\mathrm{V}}{\mathrm{t}}=\frac{\mathrm{LT}^{-1}}{\mathrm{~T}}\) = [LT^-1] ⇒ B = ms^-2
3. V = C ⇒ C = LT^-1 ⇒ C = ms^-1

Problems

Question 1.
In the expression P = E l² m^-5 G^-2 the quantities E, l, m and G denote energy, angular momentum, mass and gravitational constant respectively. Show that P is a dimension-less quantity.
Solution:
P = E L² m^-5 G^-2
Energy (E) = [ML² T^-2]
Angular momentum (L) = ML² T^-1
Mass = [M]
Universal gravitational constant
(G) = [M^-1L³T^-2]
P = [ML² T^-2] [ML² T^-1]² [M]^-5 [M^-1 L³ T^-2]^-2
P = M^1+2-5+2 L^2+4-6 T^-2-2+4
P = [M⁰ L⁰ T⁰]
Hence P is dimensional less quantity.

Question 2.
If the velocity of light c. Planck’s constant h and the gravitational ‘ constant G are taken as fundamental quantities : then express mass, length and time in terms of dimensions of these quantities.
Solution:
i) M ∝ G^x C^y h^z
[M¹ L⁰ T⁰] = [M^-1 L³ T^-2]^x [LT^-1]^y [ML² T^-1]^z
[M¹L⁰T⁰] = M^-x+z L^3x+y+2z T^-2x-y-z = 0
– x + z = 1, 3x + y + 2z = 0, – 2x – y – z = 0
Solving these equations, we get
x = \(\frac{-1}{2}\), y = \(\frac{1}{2}\), z = \(\frac{1}{2}\)
M = G^{\(\frac{-1}{2}\)} C^{\(\frac{1}{2}\)} h^{\(\frac{1}{2}\)}
M = \(\sqrt{\frac{\mathrm{hc}}{\mathrm{G}}}\)

ii) Length (l) ∝ G^x C^y h^z
[M⁰ L¹ T⁰] = [M^-1 L³ T^-2]^x [LT^-1]^y [ML² T^-1]^z
[M⁰L¹T⁰] = M^-x+z L^3x+y+2z T^-2x-y-z
Applying principle of homogeneity
-x + z = 0, 3x + y + 2z = 0, -2x – y – z = 0
Solving these equations, we get
x = \(\frac{1}{2}\), y = \(\frac{-3}{2}\), z = \(\frac{1}{2}\)
From equation (1), l = G^{\(\frac{1}{2}\)} C^{\(\frac{-3}{2}\)} h^{\(\frac{1}{2}\)}
Length (l) = \(\sqrt{\frac{\mathrm{Gh}}{\mathrm{C}^3}}\)

iii) Time (T) ∝ G^x C^y h^z
[M⁰ L⁰ T¹] = [M^-1 L³ T^-2]^x [LT^-1]^y [ML² T^-1]^z
[M⁰L⁰T¹] = M^-x+z L^3x+y+2z T^-2x-y-z
Applying principle of homogeneity
-x + z = 0, 3x + y + 2z = 0, -2x – y – z = 1
Solving these equations, we get
x = \(\frac{1}{2}\), y = \(\frac{-5}{2}\), z = \(\frac{1}{2}\)
From equation (1), l = G^{\(\frac{1}{2}\)} C^{\(\frac{-5}{2}\)} h^{\(\frac{1}{2}\)}
Length (l) = \(\sqrt{\frac{\mathrm{Gh}}{\mathrm{C}^5}}\)

Question 3.
An artificial satellite is revolving around a planet of mass M and radius R in a circular orbit of radius r. Using dimensional analysis show that the period of the satellite
T = \(\frac{k}{R} \sqrt{\frac{r^3}{g}}\)
where k is a dimensionless constant and g is acceleration due to gravity.
Solution:
T = \(\frac{k}{R} \sqrt{\frac{r^3}{g}}\)
L.H.S. : Time period = [T]
R.H.S. : \(\frac{k}{R} \sqrt{\frac{r^3}{g}}=\frac{1}{L} \sqrt{\frac{L^3}{L T^{-2}}}\) = [T]
∴ L.H.S. = R.H.S.
Above equation is correct.

Question 4.
State the number of significant figures in the following.
a) 6729
b) 0.024
c) 0.08240
d). 6.032
e) 4.57x
Solution:
a) 6729 – 4     Significant figures
b) 0024 – 2            ”
c) 008240 – 4         ”
d) 6.032 –  4           ”
e) 4.57 × 10⁸ – 3     ”

Question 5.
A stick has a length of 12.132 cm and another has a length of 12.4 cm. If the two sticks are placed end to end what is the total length ? If the two sticks are placed side by side, what is the difference in their lengths?
Solution:
a) Let lengths of the rods are
l₁ = 12.132 cm, l₂ = 12.4 cm
Here has one decimal place and l₁ has to be rounded to have only two decimal places.
l = l₁ + l₂ = 12.13 + 12.4 = 24.53
This is to be rounded off to have one decimal place only.
∴ The result is 24.5 cm

b) l₁ = 12.132 cm, l₂ = 12.4 cm
Here l₁ is rounded only two decimal places,
l₂ – l₁ = 12.4 – 12.13 = 0.27
This should be rounded off to have only one decimal place, l₂ – l₁ = 0.3

Question 6.
Each side of a cube is measured to be 7.203 m. What is
(i) the total surface area and
(ii) the volume of the cube, to appropriate significant figures ?
Solution:
Length of a side = 7.203 m
(i) Total surface area = 6a²
= 6 × (7.203)²
= 311.29
This should be rounded off to four significant figure as 7.203 as 4 significant figures.
∴ The result = 311.3m²

(ii) Volume of the cube = a³
= (7.203)³
= 373.71
This should be rounded off to four significant figures has 7.203 has four significant figures.
∴ Volume = 373.7 m³

Question 7.
The measured mass and volume of a body are 2.42 g and 4.7 cm³ respectively with possible errors 0.01 g and 0.1 cm³. Find the maximum error in density.
Solution:
M = 2.42 g, V = 4.7 cm³
∆M = 0.01 g, ∆V = 0.1 cm³
Density (ρ) = \(\frac{M}{V}\)
\(\frac{\Delta \rho}{\rho}=\frac{\Delta \mathrm{M}}{\mathrm{M}}+\frac{\Delta \mathrm{V}}{\mathrm{V}}=\frac{0.01}{2.42}+\frac{0.1}{4.7}\)
= 0.004 + 0.02 = 0.024
% error is \(\frac{\Delta \rho}{\rho}\) × 100 = 0.024 × 100
= 2.4% ≈ 2%

Question 8.
The error in measurement of radius of a sphere is 1%. What is the error in the measurement of volume ?
Solution:
Radius of the sphere \(\frac{\Delta \mathrm{r}}{\mathrm{r}}\) × 100 = 1%
Volume (V) = \(\frac{4}{3}\) πr³
\(\frac{\Delta \mathrm{V}}{\mathrm{V}}\) × 100 = 3 × \(\frac{\Delta \mathrm{r}}{\mathrm{r}}\) × 100 = 3 × 1% = 3%

Question 9.
The percentage error in the mass and speed are 2% and 3% respectively. What is the maximum error in kinetic energy calculated using these quantities ?
Solution:
\(\frac{\Delta \mathrm{M}}{\mathrm{M}}\) × 100 = 2%, \(\frac{\Delta \mathrm{V}}{\mathrm{V}}\) × 100 = 3%;
Kinetic energy = \(\frac{1}{2}\) mV²
\(\frac{\Delta \mathrm{K}}{\mathrm{K}}\) × 100 = \(\frac{\Delta \mathrm{M}}{\mathrm{M}}\) × 100 + 2 \(\frac{\Delta \mathrm{V}}{\mathrm{V}}\) × 100
= 2 + 2(3) = 2 + 6 = 8%

Question 10.
One mole of an ideal gas at standard temperature and pressure occupies 22.4 L (molar volume). If the size of the hydrogen molecule is about 1A°, what is the ratio of molar volume to the atomic volume of a mole of hydrogen ?
Solution:
Molar volume = 22.4 lit = 22.4 × 1000 c.c.
= 22.4 × 10^-3 m³
Diameter of the hydrogen molecule
= 1 A° = 10^-10 m
Radius (r) = \(\frac{D}{2}=\frac{10^{-10}}{2}\) = 0.5 × 10^-10 m
Volume (V) = \(\frac{4}{3}\) πr³
= \(\frac{4}{3}\) × 3.14 × (0.5 × 10^-10)³
v = \(\frac{1.57}{3}\) × 10^-30 = 0.5233 × 10^-30 m³
Atomic volume = V × Avagadro’s number (N)
= 0.5233 × 10^-30 × 6.023 × 10²³ = 3.151 × 10^-7
∴ \(\frac{\text { Molar volume }}{\text { Atomic volume }}=\frac{22.4 \times 10^{-3}}{3.151 \times 10^{-7}}\)
= 7.108 × 10^-4

Additional Problems

Note : In stating numerical answers, take care of significant figures.

Question 1.
Fill in the blanks
a) The volume of a cube of side 1 cm is equal to …………….. m³
b) The surface area of a solid cylinder of radius 2.0 cm and height 10.0 cm is equal to ……………. (mm)²
c) A vehicle moving with a speed of 18 km h^-1 covers ……………. m in 1 s
d) The relative density of lead is 11.3. Its density is …………….. g cm^-3 or …………….. kg m^-3.
Solution:
a) Here, length of slide L = 1 cm = 10^-2 m
Volume of cube = L³ = (10^-2 m)³ = 10^-6 m³

b) Here, r = 2.0 cm = 20 mm
h = 10.0 cm = 100 mm
Surface area of solid cylinder = (2rcr) × h
= 2 × \(\frac{22}{7}\) × 20 × 100 mm²
= 1.26 × 10⁴ mm²

c) Here, speed V = 18 km
h^-1 = \(\frac{18 \times 1000 \mathrm{~m}}{60 \times 60 \mathrm{~s}}\) = 5 ms^-1
∴ Distance covered in 1 second = 5 m

d) Here, relative density = 11.3
density = 11.3 g k.c = \(\frac{11.3 \times 10^{-3}}{\left(10^{-2} \mathrm{~m}\right)^3}\)
= 11.3 × 10³ kg m^-3

Question 2.
Fill in the blanks by suitable conversion of units.
a) 1 kg m² s^-2 = ………….. g cm² s^-2
b) 1 m = ………….. 1y
c) 3.0 ms^-2 = ………….. km h^-2
d) G = 6.67 × 10^-11 N m² (kg)^-2 = …………. (cm)³ s^-2 g^-1.
Solution:
a) 1 kg m² s²
= 1 × 10³ g (10² cm)²s^-2 = 10⁷ g cm² s^-2

b) We know, 1 light year = 9.46 × 10¹⁵ m
∴ 1 m = \(\frac{1}{9.46 \times 10^{15}}\) light year
= 1.053 × 10^-16 light year

c) 3ms^-2 = 3 × 10^-3 km \(\left(\frac{1}{60 \times 60} h\right)^{-2}\)
= 3 × 10^-3 × 3600 × 3600 km h^-2

d) G = 6.61 × 10^-11 Nm² kg^-2
= 6.67 × 10^-11 (kg ms^-2) m² kg^-2
= 6.67 × 10^-11 m³ s^-2 kg^-1
= 6.67 × 10^-11 (100 cm)³ s^-2 (1000 g)^-1
= 6.67 × 10^-8 cm³ s^-2 g^-1

Question 3.
A calorie is a unit of heat or energy and it equals about 4.2 J where 1J = 1 kg m² s^-2. Suppose we employ a system of units in which the unit of mass equals a kg, the unit of length equals b m, the unit of time is g s. Show that a calorie has a magnitude 4.2 a^-1b^-2 g² in terms of the new units.
Solution:
Here 1 calorie = 4.2 J = 4.2 Kg m^-3S^-1 …………… (1)
As new unit of mass = 1kg
∴ 1 kg = \(\frac{1}{\mathrm{a}}\) new unit of mass = a^-1
similarly, 1m = \(\frac{1}{\mathrm{b}}\) = b^-1
1s = \(\frac{1}{\mathrm{g}}\) = g^-1
Putting these values in eq(1), we obtains.
1 calorie = 4.2 (a^-1 new unit of mass)
(b^-1 new unit of length)²
(g^-1 new unit of time)²
1 calorie = 4.2 a^-1 b^-2 g².

Question 4.
Explain this statement clearly :
‘To call a dimensional quantity ‘large1 or ‘small’ is meaningless without specifying a standard for comparison”. In view of this, reframe the following statements wherever necessary :
a) atoms are very small objects
b) a jet plane moves with great speed
c) the mass of Jupiter is very large
d) the air inside this room contains a large number of molecules
e) a proton is much more massive than an electron
f) the speed of sound is much smaller than the speed of light.
Solution:
i) The statement is true. This is because a dimensionless quantity can be large or small only in comparison to some standard. For example, angle is dimensionless ∠θ = 60° is larger than ∠θ = 30°, but smaller than ∠θ = 90°

ii) a) The size of an atom is smaller than the sharp tin of a pin.
b) A jet plane moves faster than a superfast train.
c) The mass of Jupiter is very large compared to the mass of earth.
d) The air inside this room contains more number of molecules than in one mole of air.
e) The statement is already correct.
f) The statement is already correct.

Question 5.
A new unit of length is chosen such that the speed of light in vacuum in unity. What is the distance between the Sun and the Earth in terms of the new unit if light takes 8 min and 20 s to cover this distance ?
Solution:
We are given that velocity of light in vacuum, c = 1 new unit of length s^-1
Time taken by light of Sun to reach the Earth,
t = 8 min 20 s = 8 × 60 + 20 = 500 s
∴ Distance between the Sun and the Earth,
x = C × t =1 new unit of length s^-1 × 500 s
= 500 new units of length

Question 6.
Which of the following is the most
precise device for measuring length :
a) a vernier cuHipers with 20 divisions on the sliding scale
b) a screw gauge of pitch 1 mm and 100 divisions on the circular scale
c) an optical instrument that can measure length to within a wave-length of light ?
Solution:
The most precise device is that whose least count is minimum. Now
a) Least count of this vernier callipers
= 1 SD – 19 SD = 1 SD = \(\frac{19}{20}\) SD = \(\frac{1}{20}\) SD
= \(\frac{1}{20}\) mm = \(\frac{1}{200}\) cm = 0.005 cm

b) Least count of screw gauge
= \(\frac{\text { Pitch }}{\text { No. of divisions on circular scale }}\)
= \(\frac{1}{100}\) mm = \(\frac{1}{1000}\) cm = 0.01 cm

c) Wavelength of light,
λ = 10^-5 cm = 0.00001 cm
Obviously, the most precise measurement is with optical instrument.

Question 7.
A student measures the thickness of a human hair by looking at it through a microscope of magnification 100. He makes 20 observations and finds that the average width of the hair in the field of view of the microscope is 3.5 mm. What is the estimate on the thickness of hair ?
Soution:
Magnification m = \(\frac{\text { observed with }(\mathrm{y})}{\text { real width }(\mathrm{x})}\)
x = \(\frac{\mathrm{y}}{\mathrm{m}}=\frac{3.5 \mathrm{~mm}}{100}\) = 0.035 mm

Question 8.
Answer the following :
a) You are given a thread and a metre scale. How will you estimate the diameter of the thread ?
b) A screw gauge has a pitch of 1.0 mm and 200 divisions on the circular scale. Do you think it is possible to increase the accuracy of the screw gauge arbitrarily by increasing the number of divisions on the circular scale ?
c) The mean diameter of a thin brass rod is to be measured by vernier callipers. Why is a set of 100 measurements of the diameter expected to yield a more reliable estimate than a set of 5 measurements only ?
Solution:
a) The diameter of a thread is so small that it cannot be measured using a metre scale. We wind a number of turns of the thread on the metre scale. So that the turns are closely touching one another. Measure the length (l) of the windings on the scale which contains n number of turns.
∴ Diameter of thread = \(\frac{1}{n}\)

b) As least count
= \(\frac{\text { Pitch }}{\text { Number of divisions on circular scale }}\)
∴ Theoretically speaking, least count decreases on increasing the number of divisions on the circular scale. Hence accuracy would increase. Practically, it may not be possible to take the reading precisely due to low resolution of human eye.

c) A large number of observations will give more reliable result than smaller number of observations. This is because of probability of making a positive random error of certain magnitude is equal to that of making a negative random errors are likely to cancel and the result may be more reliable.

Question 9.
The photograph of a house occupies an area of 1.75 cm² on a 35 mm slide. The slide is projected on to a screen and the area of the house on the screen is 1.55 m². What is the linear magnification of the projector-screen arrangement.
Solution:
Here, area of object = 1.75 cm² and area of image = 1.55 m² = 1.55 × 10⁴ cm²
∴ Areal magnification = \(\frac{\text { area of image }}{\text { area of object }}\)
= \(\frac{1.55 \times 10^4}{1.75}\) = 8857
Linear magnification = \(\sqrt{8857}\) = 94.1

Question 10.
State the number of significant figures in the following :
a) 0.007 m²
b) 2.64 × 10²⁴ kg
c) 0.2370 g cm^-3
d) 6.320 J
e) 6.032 N m^-2
f) 0.0006032 m²
Solution:
The number of significant figures is as given below.
a) one
b) three
c) four
d) four
e) four
f) four

Question 11.
The length, breadth and thickness of a rectangular sheet of metal are 4.234 m, 1.005 m, and 2.01 cm respectively. Give the area and volume of the sheet to correct significant figures.
Solution:
Here, length l = 4.234 m;
Breath, b = 1.005 m
Thickness, t = 2.01 cm = 2.01 × 10^-2 m
Area of the sheet = 2(l × b + b × t + t × l)
= 2(4.234 × 1.005 + 1.005 × 0.0201 + 0.0201 × 4.234)
2(4.3604739) = 8.7209478 m²
As area can contain a maximum of three significant digits, therefore, rounding off, we get
Area = 8.72 m²
Also, volume = l × b × t
V = 4.234 × 1.005 × 0.0201
V = 0.0855289
V = 0.855 m³

Question 12.
The mass of a box measured by a grocer’s balance is 2.300 kg. Two gold pieces of masses 20.15 g and 20.17 g are added to the box. What is (a) the total mass of the box, (b) the difference in the masses of the pieces to correct significant figures ?
Solution:
Here, mass of the box, m = 2.3 kg
Mass of one gold piece,
m₁ = 20.15 g = 0.02015 kg
Mass of another gold piece,
m₂ = 20.17g = 0.02017 kg
a) Total mass = m + m₁ + m₁
= 2.3 + 0.02015 + 0.02017
= 2.34032 kg
As the result is correct only upto one place of decimal, therefore, on rounding off total mass = 2.3 kg

b) Difference in masses
= m₂ – m₁ = 20.17 – 20.15
= 0.02g (correct upto two places of decimal)

Question 13.
A physical quantity P is related to four observables a, b, c and d as follows :
P = a³b²/ (\(\sqrt{c}\)d )
The percentage errors of measurement in a, b, c and d are 1%, 3%, 4% and 2%, respectively. What is the percentage error in the quantity P ? If the value of P calculated using the above relation turns out to be 3.763, to what value should you round off the result ?
Solution:
Here, P = \(\frac{a^3 b^2}{\sqrt{c} d}\)
Maximum fractional error in P is given by \(\frac{\Delta \mathrm{P}}{\mathrm{P}}\)
= \(3 \frac{\Delta \mathrm{a}}{\mathrm{a}}+2 \frac{\Delta \mathrm{b}}{\mathrm{b}}+\frac{1}{2} \frac{\Delta \mathrm{c}}{\mathrm{c}}+\frac{\Delta \mathrm{d}}{\mathrm{d}}\)
= \(3\left(\frac{1}{100}\right)+2\left(\frac{3}{100}\right)+\frac{1}{2}\left(\frac{4}{100}\right)+\frac{2}{100}\)
= \(\frac{13}{100}\) = 0.13
Percentage error in
P = \(\frac{\Delta \mathrm{P}}{\mathrm{P}}\) × 100 = 0.13 × 100 = 13%
As the result (13% error) has two significant figures, therefore if P turns out to be 3.763, the result would be rounded of to 3.8.

Question 14.
A book with many printing errors contains four different formulas for the displacement y of a particle undergoing a certain periodic motion :
a) y = a sin 2 π t/T) b) y = a sin vt,
c) y = (a/T) sin t/a,
d) y = (a\(\sqrt{2}\)) (sin 2πt /T + cos 2 πt/T)
(a = maximum displacement of the particle, v = speed of the particle. T = time- period of motion). Rule out the wrong formulas on dimensional grounds.
Solution:
The argument of a trigonometrical function i.e., angle is dimensionless. Now in
a) \(\frac{2 \pi t}{T}=\frac{T}{T}\) = 1 = (M⁰L⁰T⁰)
…………… dimensionless
b) vt = (LF^-1) (T) = L = (M⁰L¹T⁰)
………….. not dimensionless

c) \(\frac{\mathrm{t}}{\mathrm{a}}=\frac{\mathrm{T}}{\mathrm{L}}\) = (L^-1T^-1)
………….. not dimensionless

d) \(\frac{2 \pi t}{\mathrm{~T}}=\frac{\mathrm{T}}{\mathrm{T}}\) = 1 = [M⁰L⁰T⁰]
…………… dimensionless

Question 15.
A famous relation in physics relates ‘moving mass’ m to the ‘rest mass’ m0 of a particle in terms of its speed v and the speed of light, c. (This relation first arose as a consequence of special relativity due to Albert Einsterin). A boy recalls the relation almost correctly but for-gets where to put the constant c. He writes :
m = \(\frac{m_0}{\left(1-v^2\right)^{1 / 2}}\)
Guess where to put the missing c.
Solution:
According to the principle of homogenity of dimensions power of M, L, T on either side of the formula must be equal. For this, on RHS, the denominator (1 – v²)^1/2 should be dimensionless. Therefore, instead of (1 – v²)^1/2,
we should write \(\left(\frac{1-v^2}{c^2}\right)^{1 / 2}\)
Hence the correct formula would be
m = \(\frac{m_0}{\left(\frac{1-v^2}{c^2}\right)^{1 / 2}}\)

Question 16.
The unit of length convenient on the atomic scale is known as an angstrom and is denoted byA° : 1A° = 1010m. The size of a hydrogen atom is about 0.5 A°. What is the total atomic volume in m³ of a mole of hydrogen atoms ?
Solution:
Here r = 0.5 A° = 0.5 × 10^-10 m
Volume of each atom of hydrogen = \(\frac{4}{3}\)πr³
= \(\frac{4}{3}\) × 3.14(0.5 × 10^-10) = 5.236 × 10^-31 m³
Number of hydrogen atoms in one gram mole of hydrogen = Avagadro’s number
= 6.023 × 10²³
∴ Atomic volume of one gram mole of hydrogen atom
= 5.236 × 10^-31 × 6.023 × 10²³
= 3.154 × 10^-7 m³

Question 17.
One mole of an ideal gas at standard temperature and pressure occupies 22.4 L of (molar volume). What is the ratio of molar volume to the atomic volume of a mole of hydrogen ? (Take the size of hydrogen molecule to about 1A°). Why is this ratio so large ?
Solution:
Atomic volume = \(\frac{4}{3}\)πR³ × N
= \(\frac{4}{3}\) (0.5 × 10^-10)³ × 6.023 × 10²³
= 3.154 × 10^-7 m³
Molar volume = 22.4 lit = 22.4 × 10^-3 m³
\(\frac{\text { Molar volume }}{\text { Atomic volume }}=\frac{22.4 \times 10^{-3}}{3.154 \times 10^{-7}}\) = 7.1 × 10⁴
The ratio is large due to large intermolecular separations.

Question 18.
Explain this common observation clearly: If you look out of the window of a fast moving train, the nearby tr6es, houses etc., seem to move rapidly in a direction opposite to the train’s motion, but the distant objects (hill tops, the Moon, the stars etc.) seem to be stationary. (In fact, since you are aware that you are moving; these distant objects seem to move with you).
Solution:
The line joining the object to the eye is called the line of sight. When a train moves rapidly, the line of sight of a near by tree changes its direction of motion rapidly. Therefore, the trees appear to run in opposite direction. On the contrary, the line of sight of far off objects does not change its direction. So much, due to extremely large distance from the eye. Hence distant hill tops, moon, the stars etc., appear stationary.

Question 19.
The principle of ‘parallax’ in section 2.3.1 is used in the determination of distances of very distant stars. The baseline AB is the line joining the Earth’s two locations six months apart 21. in its orbit around the Sun. That is, the baseline is about the diameter of the Earth’s orbit 3 × 10¹¹ m. However, even the nearest stars are so distant that with such a long baseline, they show parallax only of the order of 1″ (second) of arc or so. A parsec is a convenient unit of length on the astronomical scale. It is the distance of an object that will show a parallax of 1″ (second) of arc from opposite ends of a baseline equal to the distance from the Earth to Sol. the Sun. How much is a parsec in terms of metres ?
Solution:
Here, length of baseline
= distance from each to the sun
= 1 A.U = 1.5 × 10¹¹ m
Parallax angle, θ = 1
\(\frac{1^1}{60}=\frac{1^{\circ}}{60 \times 60}=\frac{\pi}{180} \times \frac{1}{60 \times 60}\) radian
r = 1 par sec = ?; From l = rθ = \(\frac{l}{\theta}\)
= \(\frac{1.5 \times 10^{\prime \prime}}{\pi / 180 \times 60 \times 60} \mathrm{~m}\) = 3.1 × 10¹⁶ m
Hence 1 parsec = 3.1 × 10¹⁶ m

Question 20.
The nearest star to our solar system is 4.29 light years away. How much is this distance in terms of parasecs ? How much parallax would this star (named Alpha Centauri) show when viewed from two locations of the Earth six months apart in its orbit around the Sun ?
Solution:
x = 4.29 ly = 4.29 × 9.46 × 10¹⁵ m
= \(\frac{4.29 \times 9.46 \times 10^{15}}{3.08 \times 10^{16}}\) par sec
= 1.323 par sec
θ = \(\frac{l}{r}=\frac{2 A u}{x}\)
= \(\frac{2 \times 1.496 \times 10^4}{4.29 \times 9.46 \times 10^{15}}\) radian = 1.512 sec

Question 21.
Precise measurements of physical quantities are a need of science. For example, to ascertain the speed of an aircraft, one must have an accurate method to find its positions at closely separated instants of time. This was the actual motivation behind the discovery of radar in World War II. Think of different examples in modem science where precise measurements of length, time, mass etc., are needed. Also, wherever you can, give a quantitative idea of the precision needed.
Solution:
Precise measurements of physical quantities like length, mass and time are the primary requirements for development of quantitative laws of physics or any other science. For example, in the measurement of distance of moon from earth by laser beam, very accurate measurement of time taken is required. Similarly, for measuring distance, elevation and velocity of an aeroplane by radar method, time measurement has to be accurate. For measuring distances of near by stars, accurate measurement of parallax angle is required.

In the field of crystallography, precise measurement of length is needed to determine interatomic distances using a mass spectrometer, the precision measurement of masses of atoms are made.

Question 22.
Just as precise measurements are necessary in science, it is equally important to be able to make rough estimates of quantities using rudimentary ideas and common observations. Think of ways by which you can estimate the following (where an estimate is difficult to obtain, try to get an upper bound on the quantity):
a) the total mass of rain-bearing clouds over India during the Monsoon
b) the mass of an elephant
c) the wind speed during a storm
d) the number of strands of hair on * your head
e) the number of air molecules in your classroom.
Solution:
a) During the Monsoon, meteorologist record about 100 cm of rainfall, i.e.,
h – 100 cm = 1m
Area of our country,
A = 3.3 million square km
= 3.3 × 10⁶ (10³m²)
= 3.3 × 10¹² m⁶
∴ Volume of rain water,
v = A × h = 3.3 × 10¹² 1m³
As density of water,
P = 103 km/m³
∴ Mass of rain water
= vP = 3.3 × 10¹² × 10³ kg
= 3.3 × 10¹⁵ kg
This must be the total mass of rain bearing clouds over India.

b) To estimate the mass of an elephant, we take a boat of known base area A. Measure the depth of boat in water. Let it be x₁. Therefore, volume of water displaced by the boat , V₁ = Ax₁ move the elephant into this boat. The boat gets deeper into water. Measure the depth of boat now into water, Let it be x₁
∴ Volume of water displaced by boat and elephant V₂ = Ax₂
∴ Volume of water displaced by the elephant V = V₂ – V₁ = A(x₂ – x₁)
If ρ is density of water, then mass of elephant
= mass of water displaced by it
= V_ρ = A(X₂ – X₁) ρ

c) The wind speed during a storm can be estimated using a gas filled balloon. In figure OA is normal position of a gas filled balloon, when there is no wind. As the wind blows to the right, the balloon drifts to position B in one second. The angle of drift ∠AOB = θ is measured, if h is the height of the balloon, then AB = d = hθ This is the distance travelled by the balloon in one second it must be the wind speed.

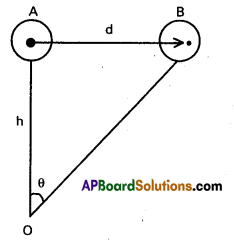
d) For this, we measure the area of the head . that carrier the hair let it be A. Using a screw guage, we measure thickness of hair, let it bad.
∴ Area of cross section of hair = πd²
Assuming that the distribution of hair over the head is uniform.
The number of strands of hair
= \(\frac{\text { total area }}{\text { area of cross section of each hair }}=\frac{\mathrm{A}}{\pi \mathrm{d}^2}\)
Calculations show that number of strands of hair on human head is of the order of one million.

e) Measure the volume of room. We know that one mole of air at NTP occupies a volume of 22.4 lit i.e., 22.4 × 10^-3 m³
∴ Number of air molecules in 22.4 × 10^-3 m³ = 6.023 × 10²³
Number of air molecules in volume v of room = \(\frac{6.023 \times 10^{23}}{22.4 \times 10^{-3}}\)v

Question 23.
The Sun is a hot plasma (ionized matter) with its inner core at a temperature exceeding 10⁷ K and its outer surface at a temperature of about 6000 K. At these high temperatures, no substance remains in a solid of liquid phase. In what range do you expect the mass density of the Sun to be, in the range of densities of solids and liquids or gases ? Check if your guess is correct from the following data : mass of the Sun = 2.0 × 10³⁰ kg, radius of the Sun = 7.0 × 10⁸ m.
Solution:
Here, M = 2.0 × 10³⁰ kg; R = 7.0 × 10⁸ m
Density ρ = ?
ρ = \(\frac{\text { mass }}{\text { volume }}=\frac{M}{\frac{4}{3} \pi R^3}=\frac{3 M}{4 \pi R^3}\)
= \(\frac{3 \times 2.0 \times 10^{30}}{4 \times 3.14 \times\left(7 \times 10^8\right)^3}\)
= 1.392 × 10³ kg/m³
This is the order of density of solids and liquids; and not gases.
The high density of Sun is due to inward gravitational attraction on outer layers, due to inner layers of the Sun.

Question 24.
When the planet Jupiter is at a distance of 824.7 million kilometers from the Earth, its angular diameter is measured to be 35.72, of arc. Calculate the diameter of Jupiter.
Solution:
Here, r = 824.7 × 10⁶ km
θ = 35.72″ radian
= \(\frac{35.72}{60 \times 60} \times \frac{\pi}{180}\) radian
Diameter, l = ?; As l = rθ
∴ l = 824.7 × 10⁶ × \(\frac{35.72 \times \pi}{60 \times 60 \times 180}\) km
= 1.429 × 10⁵km

Question 25.
A man walking briskly in rain with speed u must slant his umbrella forward making an angle q with the vertical. A student derives the following relation between q and v : tan θ = v and checks that the relation has a correct limit: as v → 0, θ →0, as expected. (We are assuming there is no strong wind and that the rain falls vertically for a stationary man). Do you think this relation can be correct ? If not, guess the correct relation.
Solution:
The relation tan θ = v has a correct limit, as v → 0, θ → 0.
However, RHS = tan θ = [M⁰L⁰T⁰] and L.H.S = v = [M⁰L¹T^-1]
Therefore, the relation is not correct dimensionally.
We shall find the correct relation is
tan θ = \(\frac{\mathrm{v^2}}{\mathrm{rg}}\)

Question 26.
It is claimed that two cesium clocks, if allowed to run for 100 years, free from any disturbance, may differ by only about 0.02 s. What does this imply for the accuracy of the standard cesium clock in measuring a time-interval of 1 s ?
Solution:
Error in 100 years = 0.02s
Error in 1 sec

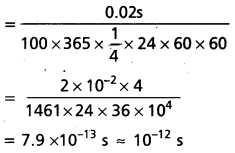
Hence the accuracy of the standard cesium clock is measuring a time interval of 1s is 10^-12 s.

Question 27.
Estimate the average mass density of a sodium atom assuming its size to be about 2.5 A°. (Use the known values of Avogadro’s number and the atomic mass of sodium). Compare it with the density of sodium in its crystalline phase: 970 kg m^-3. Are the two densities of the same order of magnitude ? If so why ?
Solution:
Atomic volume = \(\frac{4}{3}\)πR³ × N
= \(\frac{4}{3}\) × \(\frac{22}{7}\) (1.25 × 10^-10)³ 6.023 × 10²³ m
= 4.93 × 10^-6 m³
Average mass density
= \(\frac{\text { mass }}{\text { volume }}=\frac{23 \times 10^{-3}}{4.93 \times 10^{-6}}\)
= 4.67 × 10³ kg/m³
The two densities are not of the same order. This is due to interatomic spacing in the crystalline phase.

Question 28.
The unit of length convenient on the nuclear scale is a fermi: 1 f = 10^-15 m. Nuclear sizes obey roughly the following empirical relation :
r = r₀A^1/3
where r is the radius of the nucleus. A its mass number, and r₀ is a constant equal to about 1.2 f. Show that the rule implies that nuclear mass density is nearly constant for different density of a sodium atom obtained in Exercise. 27.
Answer:
Let m be the average mass of nucleon (neutron or proton)
As the nucleus contains A nucleons,
∴ mass of nucleus μ = mA
Radius of nucleus r = r₀A^1/3
Nuclear density ρ = \(\frac{\text { mass }}{\text { volume }}=\frac{\mu}{\frac{4}{3} \pi r^3}\)
= \(\frac{3 m A}{4 \pi\left(r_0 A^{1 / 3}\right)^3}=\frac{3 m}{4 \pi r_0^3}\)
As m and r₀ are constant, therefore, nuclear density is constant for all nuclei.
using m = 1.66 × 10^-27 kg and r₀
= 1.2f = 1.2 × 10^-15 m
We get ρ = \(\frac{3 m}{4 \pi r_0^3}=\frac{3 \times 1.66 \times 10^{-27}}{4 \times 3.14\left(1.2 \times 10^{-15}\right)^3}\)
= 2.29 × 10¹⁷ kg m^-3
As ρ is constant for all nuclei, this must be the density of sodium nucleus also.
Density of sodium atom
ρ’ = 4.67 × 10³ kg m^-3
= \(\frac{\rho}{\rho^{\prime}}=\frac{2.29 \times 10^{17}}{4.67 \times 10^3}\) = 4.67 × 10^-3

Question 29.
A LASER is a source or very intense, monochromatic and unidirectional beam of light. These properties of a laser light can be exploited to measure long distances. The distance of the Moon from the Earth has been already determined very precisely using a laser as a source of light. A laser light beamed at the Moon takes 2.56 s to return after reflection at the Moon’s surface. How much is the radius of the lunar orbit around the Earth ?
Solution:
Here, t = 2.56s
Velocity of laser light in vacuum,
c = 3 × 10⁸ m/s
The radius of lunar orbit is the distance of moon from the earth. Let it be x.
As x = \(\frac{c \times t}{2}\)
∴ x = \(\frac{3 \times 10^8 \times 2.56}{2}\) = 3 84 × 10⁸ m

Question 30.
A SONAR (sound navigation and ranging) uses ultrasonic waves to detect and locate objects under water. In a submarine equipped with a SONAR the time delay between generation of a probe wave and the reception of its echo after reflection from an enemy submarine is found to be 77.0 s. What is the distance of the enemy submarine? (Speed of sound in waiter = 1450 ms^-1).
Solution:
Here, t = 77.0 s, x = ? V = 1450 ms^-1
As x = \(\frac{\mathrm{V} \times \mathrm{t}}{2}\)
= \(\frac{1450 \times 77.0}{2}\)m; x = 55825 m

Question 31.
The farthest objects in our Universe discovered by modern astronomers are so distant that light emitted by them takes billions of years to reach the Earth. These objects (known as quasars) have many puzzlingn features, which have not yet been satisfactorily explained. What is the distance in km of a quasar from which light takes 3.0 billion years to reach us ?
Solution:
Here, x = ?
Time taken t = 30 billion years = 3 × 10⁹ yr
= 3 × 10⁹ × 365 × 24 × 60 × 60 s
Velocity of light in vacuum, c = 3 × 10⁸ m/s
= 3 × 10⁵ km/s
As distance = velocity × time
x = (3 × 10⁵) × 3 × 10⁹ × 365 × 24 × 60 × 60 km.
= 2.84 × 10²² km

Question 32.
It is a well known fact that during a total solar eclipse the disk of the moon almost completely covers the disk of the Sun. From this fact and from the information you can gather from examples 3 and 4. determine the approximate diameter of the moon.
Solution:
Distance of moon from earth,
ME = 3.84 × 10⁸ m
Distance of Sun from earth,

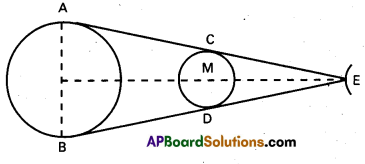
SE = 1.496 × 10¹¹ m
Distance of Sun AB = 1.39 × 10⁹ m
The situation during total solar eclipse is shown in figure.
As ∆^s ABE of CDE are similar, therefore,
\(\frac{A B}{C D}=\frac{S E}{M E}\)
CD = AB × \(\frac{M E}{S E}=\frac{1.39 \times 10^9 \times 3.84 \times 10^8}{1.496 \times 10^{11}}\)
= 3.5679 × 10⁶ m = 3567.9 km

Question 33.
A great physicist of this century (P.A.M. Dirac) loved playing with numerical values of Fundamental constants of nature. This led him to an interesting observation. Dirac found that from the basic constants of atomic physics (c, e, mass of electron, mass of proton) and the gravitational costant G, he could arrive at a number with the dimension of time. Further, it was a very large number, its magnitude being close to the present estimate on the age of the universe (~ 15 billion years). From the table of fundamental constants in this book, try to see if you too can construct this number (or any other interesting number you can think of). If its coincidence with the age of the universe were significant, what would this imply for the constancy of fundamental constants ?
Solution:
Trying out with basic constants of atomic physics (speed of light c, charge on electron e, mass of electron m_c, mass of proton m_p) and universal gravitational constant G, we can arrive at a quantity which has the dimensions of time. One such quantity is
t = \(\left(\frac{c^2}{4 \pi \epsilon_0}\right)^2 \times \frac{1}{m_p m_{e^2} c^3 G}\)
Put e = 1.6 × 10^-19 c
\(\frac{1}{4 \pi \epsilon_0}\) = 9 × 10⁹,
c = 3 × 10<sup8 m/s and
G = 6.67 × 10^-11 Nm² kg^-2
t = (1.6 × 10^-19)⁴ × (9 × 10⁹)² × \(\frac{1}{1.67 \times 10^{-27} \times\left(9 \times 10^{-31}\right) \times\left(3 \times 10^8\right)^3 \times 6.67 \times 10^{-11}}\)
t = 2.18 × 10¹⁶ sec; This time is of the order of age of universe.

Textual Examples

Question 1.
Calculate the angle at (a) 1° (degree) (b) V (minute of arc or arcmin) and (c) 1″ (second of arc or are second) in radians. Use 360° = 2π rad, 1° = 60′ and 1′ = 60″.
Answer:
(a) We have 360° = 2π rad
1° = (π/180) rad = 1.745 × 10^-2 rad

(b) 1′ = 60′ = 1.745 × 10^-2 rad
V = 2.908 × 10^-4 rad, 2.91 × 10^-4 rad

(c) 1′ = 60″ = 2.908 × 10^-4 rad
1″ = 4.847 × 10^-6 rad, 4.85 × 10^-6 rad.

Question 2.
A man wishes to estimate the distance of a nearby tower from him. He stands at a point A in front of the tower C and spots a very distant object O in line with AC. He then walks perpendicular to AC up to B, a distance of 100 m and looks at O and C again. Since O is very distant, the direction BO is practically the same as AO; but he finds the line of sight of C shifted from the original line of sight by an angle θ = 40° (θ is known as parallax’) estimate the distance of the tower C from his original position A.

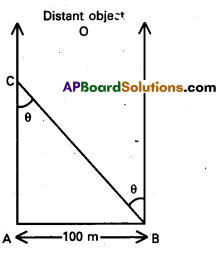
Answer:
Parallax angle θ = 40°; AB = AC tan θ
AC = AB/tan θ = 100 m/tan 40°
= 100 m/0.8391 = 119 m.

Question 3.
The moon is observed from two diametrically opposite points A and B on Earth. The angle 6 subtended at the moon by the two directions of observation is 1°54‘. Given the diameter of the Earth to be about 1.276 × 10⁷ m, compute the distance of the moon from the Earth.
Solution:
We have θ = 1°54′ = 114
= (114 × 60)” × (4.85 × 10^-6) rad
= 3.32 × 10^-2 rad.
Since 1″ = 4.85 × 10^-6,; rad
Also b = AB = 1.276 × 10⁷ m
Hence from D = b/θ, we have the earth-moon distance,
D = b/θ
= \(\frac{1.276 \times 10^7}{3.32 \times 10^{-2}}\) = 3.84 × 10⁸ m.

Question 4.
The Sun’s angular diamater is mea-sured to be 1920″. The distance D of the Sun from the Earth is 1.496 × 10″ m. What is the diameter of the Sun ?
Answer:
Sun’s angular diameter α = 1920”
= 1920 × 4.85 × 10^-6 rad
= 9.31 × 10^-3 rad
Sun’s diameter d = α
D = (9.31 × 10^-3) × (1.496 × 10¹¹) m
= 1.39 × 10⁹ m.

Question 5.
If the size of a nucleus in the range of 10^-15 to 10^-14 m) is scaled up to the tip of a sharp pin, what roughly is the size of an atom ? Assume tip of the pin to be in the range 10^-5 m to 10^-4 m.
Answer:
The size of a nucleus is in the range of 10^-15m and 10^-14 m. The tip of a sharp pin is taken to be in the range of 10^-5 m and 10^-4 m. Thus we are scaling up by a factor of 10¹⁰. An atom roughly of size 10^-10 m will be scaled up to a size of 1 m. Thus a nucleus in an atom is as small in size as the tip of a sharp pin placed at the centre of a sphere of radius about a metre long.

Question 6.
Two clocks are being tested against a standard clock located in a national laboratory. At 12 : 00 : 00 noon by the standard dock, the readings of the two clocks are :

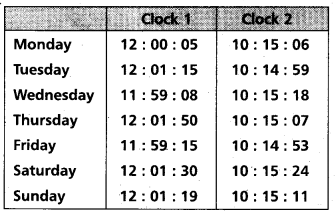
If you are doing an experiment that requires ‘precision time interval’ measurements, which of the two clocks will you prefer ?
Answer:
The range of variation over the seven days of observations is 162 s for clock 1 and 31 s for clock 2. The average reading of clock 1 is much closer to the standard time than the average reading of clock 2. The important point is that a clock’s zero error is not as significant for precision work as its variation, because a ‘zero-error’ can always be easily corrected. Hence clock 2 is to be preferred to clock 1.

Question 7.
We measure the period of oscillation of a simple pendulum. In successive measurements, the readings turn out to be 2.63 s. 2.56 s, 2.42 s, 2.71 is and 2.80 s. Calculate the absolute errors relative error or percentage error.
Answer:
The mean period of oscillation of the pendulum
T = \(\frac{(2.63+2.56+2.42+2.71+2.80) s}{5}\)
= \(\frac{13.22}{5}\) s = 2.624 s = 2.62 s
As the periods are measured to a resolution of 0.01 s, all times are to the second decimal; it is proper to put this mean period also to the second decimal.
The errors in the measurements are
2.63 s – 2.62 s = 0.01 s
2.56 s – 2.62 s = -0.06 s
2.42 s – 2.62 s = -0.20 s
2.71 s – 2.62 s = 0.09 s
2.80 s – 2.62 s = 0.18 s
Note that the errors have the same units as the quantity to be measured.
The arithmetic mean of all the absolute errors (for arithmetic mean, we take only the magnitudes) is
∆T_mean = [(0.01 + 0.06 + 0.20 + 0.09 + 0.18)s]/5 = 0.54 s/5 = 0.11 s
That means, the period of oscillation of the simple pendulum is (2.62 ± 0.11) s i.e. it lies between (2.62 + 0.11) s and (2.62 – 0.11) s or between 2.73 s and 2.51 s. As the arithmetic mean of all the absolute errors is 0.11 s, there is already an error in the tenth of a second. Hence there is no point in giving the period to a hundredth. A more correct way will be to write T = 2.6 ± 0.1 s

Note that the last numeral 6 is unreliable, since it may be anything between 5 and 7. We indicate this by saying that the measurement has two significant figures. In this case, the two significant figures are 2, which is reliable and 6, which has an error associated with it. You will learn more about the significant figures in section 2.7.
For this example, the relative error or the percentage error is δa = \(\frac{0.1}{2.6}\) × 100 = 4.

Question 8.
The temperatures of two bodies measured by a thermometer are t₁ = 20 °C ± 0.5 °C and t₂ = 50 °C ± 0.5°C. Calculate the temperature difference and the error therein.
Answer:
t’ = t₂ – t₁
= (50 °C ± 0.5 °C) – (20 °C ± 0.5 °C)
t’ = 30 °C ± 1 °C.

Question 9.
The resistance R = V/I where V = (100 ± 5) V and I = (10 ± 0.2) A. Find the percentage error in R.
Answer:
The percentage error in V is 5 and in I it is 2.
The total error in R would therefore be 5 + 2 = 7%.

Question 10.
Two resistors of resistances R₁ = 100 ± 3 ohm and R₂ = 200 ± 4 ohm are connected (a) in series, (b) in parallel. Find the equivalent resistance of the (a) series combination, (b) parallel combination. Use for (a) the relation R
= R₁ + R₂ and for (b) \(\frac{1}{R^{\prime}}+\frac{1}{R_1}+\frac{1}{R_2}\) and \(\frac{\Delta R^{\prime}}{R^{\prime 2}}=\frac{\Delta R_1}{R_1^2}+\frac{\Delta R_2}{R_2^2}\)
Answer:
a) The equivalent resistance of series, combination
R = R₁ + R₂ = (100 ± 3)
ohm + (200 ± 4) ohm = 300 ± 7 ohm.

b) The equivalent resistance of parallel combination

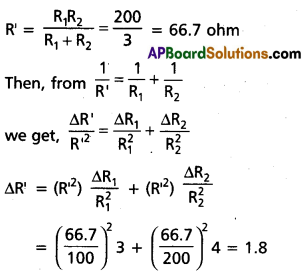
Then, R’ = 66.7 ± 1.8 ohm
(Here, ∆R is expressed as 1.8 instead of 2 to keep in conformity with the rules of significant figures).

Question 11.
Find the relative error in Z, if Z = A⁴B^1/3/CD^3/2.
Answer:
The relative error in Z is ∆Z/Z = 4(∆A/A) + (1/3) (∆B/B) + (∆C/C) + (3/2) (∆D/D).

Question 12.
The period of oscillation of a simple pendulum is T = \(2 \pi \sqrt{L / g}\). Measured value of L is 20.0 cm known to 1 mm accuracy and time for 100 oscillations of the pendulum is found to be 90 s using a wrist watch of 1s resolution. What is the accuracy in the determination of g ?
Answer:
g = 4π²L/T²; Here, T = \(\frac{t}{n}\) and ∆T = \(\frac{\Delta t}{n}\)
Therefore, \(\frac{\Delta \mathrm{T}}{\mathrm{T}}=\frac{\Delta \mathrm{t}}{\mathrm{t}}\)
The errors in both L and t are the least count errors. Therefore, (∆g/g) = (∆L/L) + 2(∆T/T)
= \(\frac{0.1}{20.0}+2\left(\frac{1}{90}\right)\) = 0.027
Thus, the percentage error in g is 100 (∆g/g)
= 100(∆L/L) + 2 × 100 (∆T/T) = 3.

Question 13.
Each side of a cube is measured to be 7.203 m. What are the total surface area and the volume of the cube to appro¬priate significant figures ?
Answer:
The number of significant figures in the measured length is 4. The calculated area and the volume should therefore be rounded off to 4 significant figures.
Surface area of the cube = 6(7.203)² m²
= 311.299254 m²
= 311.3 m²
Volume of the cube = (7.203)³ m³
= 373.714754 m³
= 373.7 m³

Question 14.
5.74 g of a substance occupies 1.2 cm³. Express its density by keeping the significant figures in view.
Answer:
There are 3 significant figures in the measured mass whereas there are only 2 significant figures in the measured volume. Hence the density should be expressed to only 2 significant figures.
Density = \(\frac{5.74}{1.2}\) cm^-3 = 4.8 g cm^-3.

Question 15.
Let us consider an equation \(\frac{1}{2}\) mv² = mgh where m is the mass of the body, v its velocity, g is the acceleration due to gravity and h is the height. Check whether this equation is dimensionally correct.
Answer:
The dimensions of LHS are
[M] [LT^-1]² = [M] [L²T^-2] = [M L²T^-2]
The dimensions of RHS are
[M] [LT^-2] [L] = [M] [L²T^-2] = [M L²T^-2]
The dimensions of LHS and RHS are the same and hence the equation is dimensionally correct.

Question 16.
The SI unit of energy is J = kg m²s^-2; that of speed v is ms-1 and of acceleration a is ms^-2. Which of the formulae for kinetic energy (K) given below can you rule out on the basis of dimensional arguments (m stands for the mass of the body):
(a) K = m²V³
(b) K = (1/2) mv²
(c) K = ma
(d) K = (3/16) mv²
(e) K = (1/2) mv² + ma.
Answer:
Every correct formula or equation must have the same dimensions on both sides of the equation. Also, only quantities with the same physical dimensions can be added or subtracted. The dimensions of the quantity on the right side are [M² L³ T^-3] for (a) : [ML²T^-2] for (b) and (d); [MLT^-2] for (c). The quantity on the right side of (e) has no proper dimensions since two quantities of different dimensions have been added. Since the kinetic energy K has the dimensions of [ML²T^-2], formulas (a), (c) and (e) are ruled out. Note that dimensional arguments cannot tell which of the two, (b) or (d), is the correct formula. For this, one must turn to the actual definition of kinetic energy. The correct formula for kinetic energy is given by (b).

Question 17.
Consider a simple pendulum, having a bob attached to a string, that oscillates under the action of the force of gravity. Suppose that the period of oscillation of the simple pendulum depends on its length (l), mass of the bob (m) and acceleration due to gravity (g). Derive the expression for its period using method of dimensions.
Answer:
The dependence of time period T on the quantities l, g and m as a product may be written as :
T = k lx g^y m^z
Where k is dimensionless constant and x, y and z are the exponents.
By considering dimensions on both sides, we have
[L°M°T¹] = [L¹]x [L¹T^-2]y [M¹]² = L^x+yT^-2y M^z
On equating the dimensions on both sides, we have
x + y = 0; -2y = 1 and z = 0
So that x = \(\frac{1}{2}\), y = \(\frac{1}{2}\), z = 0
Then, T = kl^1/2 g^1/2 or T = \(\mathrm{k} \sqrt{\frac{l}{\mathrm{~g}}}\)
Note that value of constant k can hot be obtained by the method of dimensions. Here it does not matter if some number multiplies the right side of this formula because that does not affect its dimensions.
Actually, k = 2π so that T = \(2 \pi \sqrt{\frac{l}{g}}\)