Andhra Pradesh BIEAP AP Inter 1st Year Physics Study Material 3rd Lesson Motion in a Straight Line Textbook Questions and Answers.
AP Inter 1st Year Physics Study Material 3rd Lesson Motion in a Straight Line
Very Short Answer Questions
Question 1.
The states of motion and rest are relative. Explain.
Answer:
Rest and motion are relative. They are not absolute. A body can be in the rest or in motion w.r.t. reference frame. A man in a moving train is a rest w.r. to a co-passenger, but he is in motion w.r.t a man on the ground.
Question 2.
How is average velocity different from instantaneous velocity? [Mar. 13]
Answer:
The average velocity does not give any details of the motion of the particle. It gives only the result of the motion. The instantaneous velocity defines how fast the particle moves at a particular instant of time.
In uniform motion, the instantaneous velocity is equal to the average velocity.
![]()
Question 3.
Give an example where the velocity of an object is zero but its acceleration is not zero.
Answer:
When the body is projected vertically upwards, at the highest point, its velocity is zero. But its acceleration (a = g) is not equal to zero.
Question 4.
A vehicle travels half the distance L with speed v1 and the other half with speed v2. What is the average speed ?
Answer:
Average speed = \(\frac{\text { Total length of the path }}{\text { Total time taken }}=\frac{\mathrm{L}}{\frac{\left(\frac{\mathrm{L}}{2}\right)}{\mathrm{V}_1}+\frac{\left(\frac{\mathrm{L}}{2}\right)}{\mathrm{V}_2}}=\frac{2 \mathrm{~V}_1 \mathrm{~V}_2}{\mathrm{~V}_1+\mathrm{V}_2}\)
Question 5.
A lift coming down is just about to reach the ground floor. Taking the ground floor as origin and positive direction upwards for all quantities, which one of the following is correct
a) x < 0, v < 0, a > 0, b) x > 0, v < 0, a < 0, c) x > 0, v < 0, a > 0, d)x > 0, V > 0, a > 0
Answer:
While lift is moving towards ground floor (origin), position x decreases, velocity decreases. Hence x < 0, v < 0. But a > 0. So(a) is correct option.
Question 6.
A uniformly moving cricket ball is hit with a bat for a very short time and is turned back. Show the variation of its acceleration with time taking the acceleration in the backward direction as positive.
Answer:
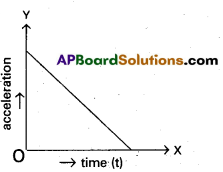
Question 7.
Give an example of one-dimensional motion where a particle moving along the positive x-direction comes to rest periodically and moves forward.
Answer:
When simple harmonic oscillator starts from left extreme position and comes to rest at that point periodically and moves forward.
![]()
Question 8.
An object falling through a fluid is observed to have an acceleration given by a = g – bv where g is the gravitational accelaration and b is a constant. After a long time it is observed to fall with a constant velocity. What would be the value of this constant velocity ?
Answer:
Given acceleration a = g – bv
\(\frac{\mathrm{dv}}{\mathrm{dt}}\) = g – bv [∵ a = \(\frac{\mathrm{dv}}{\mathrm{dt}}\)]
If an object is moving through fluid with constant velocity, dv = 0
0 = g – bv ∴ v = \(\frac{\mathrm{g}}{\mathrm{b}}\)
Question 9.
If the trajectory of a body is parabolic in one frame, can it be parabolic in another frame that moves with a constant velocity with respect to the first frame ? If not, what can it be ?
Answer:
No. the trajectory is a vertical straight line.
Question 10.
A spring with one end attached to a mass and the other to a rigid support is stretched and released. When is the magnitude of acceleration a maximum ?
Answer:
The magnitude of acceleration is maximum at Extreme Positions.
Short Answer Questions
Question 1.
Can the equations of kinematics be used when the acceleration varies with time ? If not, what form would these equations take ?
Answer:
No, the equations of kinematics be used when the acceleration varies with time.
If an object moves along a straight line with uniform acceleration (a), equations of kinematics are
- v = v0 + at;
- x = v0t + \(\frac{1}{2}\) at2;
- v2 = v02 + 2ax
Where x is displacement, v0 is velocity at t = 0, v is velocity at time t, a is acceleration.
These are kinematic equations of rectilinear motion for constant acceleration.
If an object moves with non-uniform acceleration, the equations of motion are,
- v = v0 + at
- x = x0 + v0t + \(\frac{1}{2}\)at2
- v2 = v02 + 2a (x – x0)
![]()
Question 2.
A particle moves in a straight line with uniform acceleration. Its velocity at time t = 0 is v1 and at time t = t is v2. The average velocity of the particle in this time interval is (v1 + v2)/2. Is this correct ? Substantiate your answer.
Answer:
Consider a particle moving with uniform acceleration a.
At t = 0, the (initial) velocity = v1
At t = t, the (final) velocity = v2
time = t

∴ The given statement is true.
Question 3.
Can the velocity of an object be in a direction other than the direction of acceleration of the object ? If so, give an example.
Answer:
Yes, the velocity of an object be in a direction other than the direction of acceleration of the object.
Ex. : In the case of the upward motion of a projectile, the angle between velocity and acceleration is 180°. During its journey, the direction of velocity is in upwards and the direction of acceleration is in downwards.
![]()
Question 4.
A parachutist flying in an aeroplane jumps when it is at a height of 3 km above ground. He opens his parachute when he is about 1 km above ground. Describe his motion.
Answer:
- A parachutist is jumping from an air-plane at a height of 3 km from the ground. Upto 1 km above the ground, his motion is like a freely falling body. He falls with constant acceleration 9.8 ms-2.
- At a height of 1 km above the ground, when he opened the parachute, the air drag opposes the force of gravity resultant on it. The acceleration of parachutist gradually decreases since velocity increases (a = g – bv) and becomes zero.
- Further, the parachutist attains terminal speed (constant speed), where air drag (in upward direction) is equal to force of gravity (in downward).
- Hopefully this terminal speed is slow enough, so he can touch the ground without much difficulty.
Question 5.
A bird holds a fruit in its beak and flies parallel to the ground. It lets go of the fruit at some height. Describe the trajectory of the fruit as it falls to the ground as seen by
(a) the bird
(b) a person on the ground.
Answer:
A bird holds a fruit in its beak and flies parallel to the ground.
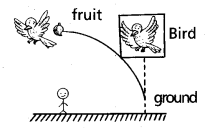
It lets go of the fruit at some height, the trajectory of the fruit as it falls to the ground as seen by (a) the bird is a straight line (b) a person on the ground is a parabola.
Question 6.
A man runs across the roof of a tall building and jumps horizontally on to the (lower) roof of an adjacent building. If his speed is 9 ms-1 and the horizontal distance between the buildings is 10 m and the height difference between the roofs is 9 m, will he be able to land on the next building ? (take g = 10 ms-2).
Answer:
Difference of heights between two buildings h = 9 m; g = 10 ms-2
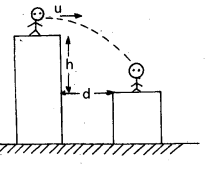
Time of flight of a man t = \(\sqrt{\frac{2 \mathrm{~h}}{\mathrm{~g}}}=\sqrt{\frac{2 \times 9}{10}}\)
= 1.341 sec
Horizontal speed of a man u = 9 ms-1
Horizontal distance travelled by a man dm
= Horizontal speed × Time of flight
= u × t = 9 × 1.341 = 12.07 m
Given, the horizontal distance between the buildings db = 10 m
Since dm > db, the man can able to land on the next building.
![]()
Question 7.
A ball is dropped from the roof of a tall building and simultaneously another ball is thrown horizontally with some velocity from the same roof. Which ball lands first? Explain your answer.
Answer:
Let height of the building = Displacement of ball = h
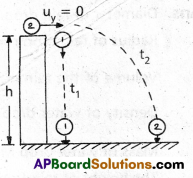
For first ball u = 0; S = h. a = g; t = t1
Substituting these values in S = ut + \(\frac{1}{2}\) at2
⇒ h = 0 + \(\frac{1}{2}\) gt12
∴ t1 = \(\sqrt{\frac{2 h}{g}}\) …………… (1)
For second ball, ux = u (say) uy = 0, aY = g, SY = h; t = t2
Substituting these values in
SY = uYt + \(\frac{1}{2}\) aYt2
h = 0 + \(\frac{1}{2}\) gt22
∴ t2 = \(\sqrt{\frac{2 h}{g}}\)
From equation (1) and equation (2), t1 = t2
∴ Two balls will reach the ground in same time.
Question 8.
A ball is dropped from a building and simultaneously another ball is projected upward with some velocity. Describe the change in relative velocities of the balls as a function of time.
Answer:
For first ball u = u1; v = v1; a = g; t = t
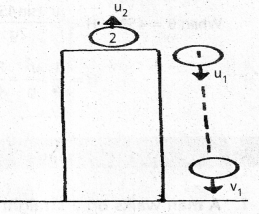
Substituting these values in equation
v = u + at, we get
v1 = u1 + gt1
For second ball u = u<sub2; v = v2; a = – g; t = t2
Substituting these values in equation, v = u + at,
We get, v2 = u2 + gt2 ………………. (2)
(1) – (2) ⇒ (v1 – v2) = (u1 – u2) + g(t1 + t2)
∴ (v1 – v2) – (u1 – u2) = g(t1 + t2)
[∵ u1 = 0]
∴ (v1 – v2) – (0 – u2) = g(t1 + t2)
∴ The change in final relative velocity and initial relative velocity of two balls = Function of time.
![]()
Question 9.
A typical raindrop is about 4 mm in diameter. If a raindrop falls from a cloud which is km above the ground, estimate its momentum when it hits the ground.
Answer:
Diameter of rain drop, D = 4 mm
Radius of ram drop r = 2 mm = 2 × 10-3 m
Volume of the rain atop, V = \(\frac{4}{3}\) πr3 = \(\frac{4}{3}\) × \(\frac{22}{7}\) × (2 × 10-3)3
Density of water drop = 103 kg/m3
Mass of water drop M = Vd = \(\frac{4}{3}\) × \(\frac{22}{7}\) × 8 × 10-9 × 103
= 33.5 × 2 × 10-6 kg
The height of raindrop falls from a cloud, h = 1 km = 1000 m
Velocity of raindrop just before touching the ground V = \(\sqrt{2 g h}=\sqrt{2 \times 9.8 \times 1000}\) = 140 ms-1
Momentum of raindrop when it hits the ground P = mV = 33.52 × 10-6 × 140 = 469.28 × 10-5
= 0.004692 kg ms-1
Question 10.
Show that the maximum height reached by a projectile launched at an angle of 45° is one quarter of its range.
Answer:
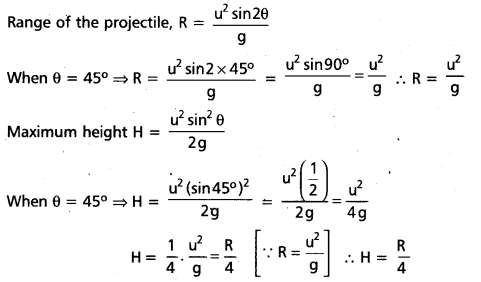
Problems
Question 1.
A man walks on a straight road from his home to a market 2.5 km away with a speed of 5 km h-1. Finding the market closed, he instantly turns and walks back home with a speed of 7.5 km h-1. What is the (a) magnitude of average velocity and (b) average speed of the man over the time interval 0 to 50 min.
Answer:
From home to market:
X1 = 2.5 km; v1 = 5 km h-1;
t1 = \(\frac{\mathrm{X_1}}{\mathrm{v_1}}=\frac{2.5}{5}=\frac{1}{2}\) h = 30 min.
From market to home:
X2 = 2.5 km; v2 = 7.5 km h-1
t2 = \(\frac{\mathrm{X_2}}{\mathrm{v_2}}=\frac{2.5}{7.5}=\frac{1}{3}\) h = 20 min.
a) Magnitude of average velocity
= \(\frac{\Delta \mathrm{X}}{\Delta \mathrm{t}}=\frac{\mathrm{X}_1-\mathrm{X}_2}{\mathrm{t}_1+\mathrm{t}_2}=\frac{2.5-2.5}{50}\) = 0
b) Average speed
= \(\frac{X_1+X_2}{t_1+t_2}=\frac{2.5-2.5}{(30+20) \min }=\frac{5 \mathrm{~km}}{50 \times \frac{h}{60}}\)
= 6 km h-1
![]()
Question 2.
A car travels the first third of a distance with a speed of 10 kmph, the second third at 20 kmph and the last third at 60 kmph. What is its mean speed over the entire distance ? [T.S. Mar 16]
Answer:
v1 = 10 km ph; v2 = 20 km ph; v1 = 60 km ph; v = ?
\(\frac{3}{v}=\frac{1}{v_1}+\frac{1}{v_2}+\frac{1}{v_3}\)
\(\frac{3}{v}=\frac{1}{10}+\frac{1}{20}+\frac{1}{60}, \frac{3}{v}=\frac{6+3+1}{60}=\frac{3}{v}=\frac{10}{60}\)
∴ v = 18 km ph
Question 3.
A bullet moving with a speed of 150 ms-1 strikes a tree and penetrates 3.5 cm before stopping. What is the magnitude of its retardation in the tree and the time taken for it to stop after striking the tree ?
Answer:
u = 150 m/s, s = 3.5 cm = 0.035 m, v = 0
v2 – u2 = 2as
0 – 1502 = 2 × a × 0.035
a = \(\left|\frac{-150 \times 150}{2 \times 0.035}\right|\)
= -3.214 × 105 m/s2 = -3.214 × 105 m/s2
Time = \(\frac{v-u}{a}=\frac{0-150}{3.214 \times 10^5}=\frac{-150}{3.214 \times 10^5}\)
= 4.67 × 10-4 sec.
Question 4.
A motorist drives north for 30 min at 85 km/h and then stop for 15 min. He continues travelling north and covers 130 km in 2 hours. What is his total displacement and average velocity ?
Answer:
v1 = 85 kmph, t = 35.0 min, S2 = 130 km
S1 = Displacement = \(\frac{85}{60}\) × 30 = 42.5 km
S2 = 130 km
a) S = S1 + S2 = 42.5 + 130 = 172.50 km
b) Avg.velocity = \(\frac{S_1+S_2+S_3}{t_1+t_2+t_3}\)
= \(\frac{42.5+0+130}{\frac{30}{60}+\frac{15}{60}+2}\)
= \(\frac{172.5 \times 60}{165}\)
= 62.7 km/hr
![]()
Question 5.
A ball A is dropped from the top of a .building and at the same time an identical ball B is thrown vertically upward from the ground. When the balls collide the speed of A is twice that of B. At what fraction of the height of the building did the collison occur ?
Answer:
Let height of the building =H
Let two balls collide at a height = h
For ball A, u = 0; V = VA s = H – h; t = t; a = g
Substituting these values in s = ut + \(\frac{1}{2}\) at2
H – h = 0 + \(\frac{1}{2}\) gt2
H – h = \(\frac{1}{2}\) gt2 …………. (1)
and VA = gt ……………… (2)
For ball B, u = u; v = vB; s = h; a = -g
Substituting these values in s = ut + \(\frac{1}{2}\) at2
⇒ h = ut – \(\frac{1}{2}\) gt2 ………. (3)
and VB = u – gt ……….. (4)
given VA = 2VB
gt = 2(u – gt)
u = \(\frac{3}{2}\) gt …………… (5)
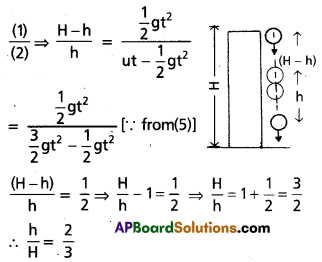
Question 6.
Drops of water fall at regular intervals from the roof of abuilding of height 16 m. The first drop strikes the ground at the same moment as the fifth drop leaves the roof. Find the distances between successive drops.
Answer:
H = 16 m
Time taken by the first drop to touch the ground t = \(\sqrt{\frac{2 \mathrm{~h}}{\mathrm{~g}}}=\sqrt{\frac{2 \times 16}{9.8}=\sqrt{3.26}}\)
sec = 1.8 sec
Time interval between two successive drops
= \(\frac{t}{n-1}\) Where n = no. of drops
= \(\frac{1.8}{5-1}=\frac{1.8}{4}\) = 0.45 sec
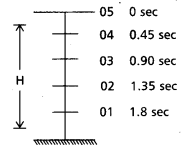
For second drop h2 = \(\frac{1}{2}\) gt2
= \(\frac{1}{2}\) × 9.8 × 1.35 × 1.35 = 8.93 m
d12 = 16 – 8.93 = 7.06 = 7 m
For 3rd drop h3 = \(\frac{1}{2}\) × 9.8 × 0.90 × 0.90
= 3.97
d23 = 8.93 – 3.97 = 4.961 = 5 m
For 4th drop h4 = \(\frac{1}{2}\) × 9.8 × 0.45 × 0.45
= 0.9922
d34 = 3.97 – 0.9922
d34 = 2.9778 = 3 m
Similarly for d45 = 0.9922 – 0 = 0.9922 = 1 m
![]()
Question 7.
A hunter aims a gun at a monkey hanging from a tree some distance away. The monkey drops from the branch at the moment he fires the gun hoping to avoid the bullet. Explain why the monkey made a wrong move.
Answer:
Suppose a hunter aims the gun at a monkey hanging from a high tree branch some distance away d. The instant the monkey observes the flash of the gun it drops from the tree.
Here the time taken by the monkey from the tree to the ground is t1 = \(\sqrt{\frac{2 h}{g}}\) ……………. (1)
The path of bullet from the gun is like a horizontal Projectile, vertical velocity uy = 0, Let S = h. Let t2 be the time taken by the bullet to reach the ground.
∴ S = ut + \(\frac{1}{2}\)a t22
S = 0 × t + \(\frac{1}{2}\)a t22
∴ h = \(\frac{1}{2}\)g t22
t2 = \(\sqrt{\frac{2 h}{g}}\) …………….. (2)
It is observed from equation (1) and (2),
t1 = t2
Both bullet and monkey reach the ground simultaneously.
Hence the bullet hits the monkey. Therefore Monkey made a wrong move.
Question 8.
A food packet is dropped from an aeroplane, moving with a speed of 360 kmph in a horizontal direction, from a height of 500 m. Find (i) its time of descent (ii) the horizontal distance between the point at which the food packet reaches the ground and the point above which it was dropped.
Answer:
Velocity of aeroplane v = 360 kmph
v = 360 × \(\frac{5}{18}\) = 100 m/s
h = 500 m
i) Time of descent =
t = \(\sqrt{\frac{2 h}{g}}=\sqrt{\frac{2 \times 500}{10}}\) = 10 sec
ii) Horizontal range R = u × \(\sqrt{\frac{2 \mathrm{~h}}{\mathrm{~g}}}\)
= 100 × 10 sec = 1000 sec
Question 9.
A ball is tossed from the window of a buliding with an initial velocity of 8 ms-1 at an angle of 20° below the horizontal. It strikes the ground 3 s later. From what height was the ball thrown ? How far from the base of the building does the ball strike the ground ?
Answer:
u = 8 m/s, θ = 20°, t = 35
a) Horizontal distance = (u cos θ) t = 8 cos 20° × 3 = 8 × 0.9397 × 3 = 22.6 m
b) Height h = (u sin θ)t + \(\frac{1}{2}\) gt2
= 8 sin 20° × 3 + \(\frac{1}{2}\) × 9.8 × 9
= 8.208 + 44.1 = 52.31 m
c) The ball is thrown from a height of 44.1 m 1
h1 = (u sin θ)t1 + \(\frac{1}{2}\) gt12
10 = (8 sin 20°)t1 + \(\frac{1}{2}\) 9.8% t12
= 2.736 t1 + 4.9 t12
⇒ 4.9 t12 + 2.736 t1 – 10 = 0
t1 = \(\frac{-2.736 \pm \sqrt{(2.736)^2+4 \times 4.9 \times 10}}{2 \times 4.9}\)
⇒ t1 = \(\frac{-2.736 \pm \sqrt{203.48}}{9.8}\)
t1 = \(\frac{-2.736+14.265}{9.8}=\frac{11.5288}{9.8}\)
= 1.176 = 1.18 sec
![]()
Question 10.
Two balls are projected from the same point in directions 30° and 60° with respect to the horizontal. What is the ratio of their initial velocities if they
(a) attain the same height ?
(b) have the same range 1
Answer:
θ1 = 30°, θ2 = 60°
a) First ball maximum height H1

Additional Problems
Question 1.
In which of the following examples of motion, can the body be considered approximately a point object:
a) a railway carriage moving without jerks between two stations.
b) a monkey sitting on top of a man cycling smoothly on a circular track.
c) a spinning cricket ball that turns sharply on hitting the ground.
d) a tumbling beaker that has slipped off the edge of a table.
Solution:
a) The carriage can be considered a point object because the distance between two stations is very large as compared to the size of the railway carriage.
b) The monkey can be considered as a point object if the cyclist describes a circular track of very large radius because in that case the distance covered by the cyclist is quite large as compared to the size of monkey. The monkey can not be considered as a point object. If the cyclist describes a circular track of small radius, because in that case the distance covered by the cyclist is not very large as compared to the size of the monkey.
c) The cricket ball can not be considered as a point object because the size of the spinning cricket ball is quite appreciable as compared to the distance through which the ball may turn on hitting the ground.
d) A beaker sleeping off the edge of a table cannot be considered as a point, object because the size of the beaker is not negligable as compared to the height of the table.
![]()
Question 2.
The position-time (x – t) graphs for two children A and B returning from their school O to their homes P and Q respectively are shown in fig. Choose the correct entries in the brackets below :

a) (A/B) lives.closer to the school than (B/A).
b) (A/B) starts from the school earlier than (B/A).
c) (A/B) walks faster than (B/A).
d) A and B reach home at the (same/ different) time.
e) (A/B) overtakes (B/A) on the road (once/twice).
Solution:
a) As OP < OQ, A lives closer to the school than B.
b) For x = 0, t = 0 for A; while t has some finite value for B.
Therefore, A starts from the school earlier than B.
c) Since the velocity is equal to slope of x -1 graph in case of uniform motion and slope of x -1 graph for B is greater than for A, hence B walks faster than A.
d) Corresponding to points P and Q, the value of t from x – t graph for A and B is same, which can be checked by drawing lines through P and Q parallel to x axis. Thus both A and B reach home at the same time.
e) The x – t graph for A and B intersect each other only once. Since B starts from the school after- wards, therefore B overtakes A on the road once.
Question 3.
A woman starts from her home at 9.00 am, walks with a speed of 5 km h-1 on a straight road up to her office 2.5 km away, stays at the office up to 5.00 pm and returns home by an auto with a speed of 25 km h-1. Choose suitable scales and plot the x-t graph of her motion.
Answer:
Time taken in reaching office
= \(\frac{\text { Distance }}{\text { Speed }}=\frac{2.5}{5}\) = 0.5 hr.
Time taken in returning from office = \(\frac{2.5}{25}\)
= 0.1 hr = 6 min
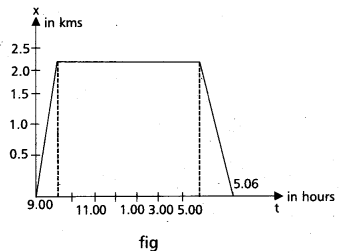
It means the woman reaches the office at 9.30 am and returns home at 5.06 p.m. The x – t graph of this motion will be as shown in fig.
![]()
Question 4.
A man walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward and so on. Each step is 1 m long and requires 1 s. Plot the x-t graph of his motion. Determine graphically and otherwise how long the drunkard takes to fall in a pit 13 m away from the start.
Answer:
The effective distance travelled by drunkard in 8 steps = 5 – 3 = 2 m.
Therefore he take 32 steps to walk 8 meters. Now he will have to cover 5 mt more to reach the pit, for which he has to take only 5 forward steps.
Therefore he will have to take = 32 + 5 = 37 steps to move 13 mts. Thus he will fall into pit after taking 37 steps i.e., after 37 seconds from the start.
Question 5.
A jet airplane travelling at the speed of 500 km h-1 ejects its products of combustion at the speed of 1500 km h-1 relative to the jet plane. What is the speed of the latter with respect to an observer on the ground ?
Answer:
Lt vp be the velocity of the products w.r.to ground
Lt us consider the direction of motion of airplane to be positive direction of x-axis.
Here, speed of jet plane vA = 500 km h-1
Relative speed of products of combustion w.r.to jet plane vρA = -1500 km h-1
Relative velocity of the products w.r.to air plane is
vPA – vP – vA = -1500
(Or)
vP = vA – 1500 = 500 – 1500
= – 1000 km h-1
Here -ve sign shows the direction of products of combustion is opposite to that of airplane. Thus the magnitude of relative velocity is 1000 km h-1.
![]()
Question 6.
A car moving along a straight highway with speed of 126 km h-1 is brought to a stop within a distance of 200 m. What is the retardation of the car (assumed uniform) and how long does it take for the car to stop ?
Answer:
Here, u = 126 km h-1 = \(\frac{126 \times 1000}{60 \times 60}\) ms-1
= 35 ms-1; v = 0, S = 200 m, a = ?
and t = ?
We know v2 = u2 + 2as
0 = (35)2 + 2 × a × 200 (Or)
a = \(\frac{-(35)^2}{2 \times 200}=\frac{-49}{16}\)
= -3.06 ms-2
As v = u + at
0 = 35 + \(\left(\frac{-49}{16}\right) \mathrm{t}\) (Or)
t = \(\frac{35 \times 16}{49}=\frac{80}{7}\) = 11.43s
Question 7.
Two trains A and B of length 400 m each are moving on two parallel tracks with a uniform speed of 72 km h-1 in the same direction, with A ahead of B. The driver of B decides to overtake A and accelerates by 1 m s-2. If after 50 s, the guard of B just moves past the driver of A, what was the original distance between them ?
Solution:
For train A; u = 72 km h-1 = \(\frac{72 \times 1000}{60 \times 60}\)
= 20 m s-2; t = 50s; a = 0, S = SA;
As S = ut + \(\frac{1}{2}\) at2
∴ SA = 20 × 50 + \(\frac{1}{2}\) × 0 × 502
= 1000 m
For train B; u = 72 kms-1 = 20 ms-2;
a = 1 ms-2, t = 50/S, S = s-B
As, S = ut + \(\frac{1}{2}\) at2
∴ SB = 20 × 50 + \(\frac{1}{2}\) × 1 × 502 = 2250 m
Taking the guard of the train B in the last compartment of the train B, it follows that original distance between two trains + length of train A + length of train B = SB – SA.
(Or) Original distance between the two trains
400 + 400 = 2250 – 1000 = 1250
(Or) Original distance between the two trains
= 1250 – 800 = 450 m
![]()
Question 8.
On a two-lane road, car A is travelling with a speed of 36 km h-1. Two cars B and C approach car A in opposite directions with a speed of 54 km h-1 each. At a certain instant, when the distance AB is equal to AC, both being 1 km, B decides to overtake A before C does. What minimum acceleration of car B is required to avoid an accident ?
Solution:
Velocity of car A = 36 km h-1 = 10 ms-1
Velocity of car B or C = 54 km h-1 = 15 ms-1
Relative velocity of B w.r.to
A = 15 – 10 = 5 ms-1
Relative velocity of C w.r.to
A = 15 + 10 = 25 ms-1
As, AB = AC = 1 km = 1000 m
Time available to B (Or) C for crossing
A = \(\frac{1000}{25}\) = 40s
If car B accelerates with acceleration a, to cross A before car C does, then
u = 5 ms-1, t = 40s, s = 1000 m, a = ?
Using s = ut + \(\frac{1}{2}\) at2
1000 = 5 × 40 + \(\frac{1}{2}\) × a × 402 (Or)
1000-200 = 800 a (Or)
a = 1 m/s2
Question 9.
Two towns A and B are connected by a regular bus service with a bus leaving in either direction every T minutes. A man cycling with a speed of 20 km h-1 in the direction A to B notices that a bus goes past him every 18 min in the direction of his motion and every 6 min in the opposite direction. What is the period T of the bus service and with what speed (assumed constant) do the buses ply on the road ?
Solution:
Let v km h-1 be the constant speed with which the buses ply between the towns A and B.
The relative velocity of the bus (for the motion A to B) w.r.to the cyclist C i.e., in the direction in which the cyclist is going = (v – 20) kmh-1.
The relative velocity of the bus from B to A W r to the cyclist = (v + 20) kmh-1.
The distance travelled by the bus in time T(min) = vT
As per question \(\frac{v T}{v-20}\) = 18 (Or) vT
= 18v – 18 × 20 ………………… (i)
and \(\frac{v T}{v+20}\) = 6 (Or) vT = 6v + 20 × 6 …………….. (ii)
Equations (i) and (ii) we get
18v- 18 × 20 = 6v + 20 × 6 (Or)
12v = 20 × 6 + 18 × 20 = 480
(Or) v = 40 kmh-1
Putting this value of v in (i) we get 40
T = 18 × 40- 18 × 20 = 18 × 20
(Or) T = 18 × 20/40 = 9 min.
![]()
Question 10.
A player throws a ball upwards with an initial speed of 29.4 ms-1.
a) What is the direction of acceleration during the upward motion of the ball ?
b) What are the velocity and accele-ration of the ball at the highest point of its motion ?
c) Choose the x = 0 m and t = 0 s to be the location and time of the ball at its highest point, vertically downward direction to be the positive direction of x-axis and give the signs of position, velocity and acceleration of the ball during its upward and downward motion.
d) To what height does the ball rise and after how long does the ball return to the player’s hands ?
(Take g = 9.8 ms-2 and neglect air resistance).
Solution:
a) Since the ball is moving under the effect of gravity, the direction of acceration due the gravity is always vertically downwards.
b) At the highest point, the velocity of the ball becomes zero and acceleration is equal to the acceleration due to gravity = 9.8 ms-2 in vertically downward direction.
c) When the highest point is chosen as the location for x = 0 and t = 0 and vertically downward direction to be positive direction of x- axis and upward direction as negative direction of x-axis.
During upward motion, sign of position is negative, sign of velocity is negative and sign of acceleration is positive.
During downward motion, sign of position is positive, sign of acceleration is also positive.
d) Let the t be time taken by the ball to reach the highest point where height from ground to be S.
Taking vertical upward motion of the ball,
we have
u = -29.4 m/s-1, a = 9.8 m/s-2,
v = 0, S = 5, t = 2
As v2 – u2 = 2as
0 – (29.4)2 = 2 × 9.8 × s (Or)
S = \(\frac{-(29.4)^2}{2 \times 9.8}\) = -44.1 m
Here -ve sign shows that distance is covered in upward direction.
As v = u + at
∴ 0 = -29.4 + 9.8 × t (or) t = \(\frac{-29.4}{9.8}\) = 3s
It means time of ascent = 3s
When an objective move under the effect of gravity alone, the time of ascent is always equal to time of descent.
Therefore total time after which the ball returns the player’s hand = 3 + 3 = 6s
Question 11.
Read each statement below carefully and state with reasons and examples, if it is true or false :
A particle in one-dimensional motion
a) with zero speed at an instant may have non-zero acceleration at that instant
b) with zero speed may have non-zero velocity.
c) with constant speed must have zero acceleration.
d) with positive value of acceleration must be speeding up.
Solution:
a) True, when a body is thrown vertically upwards in the space. Then at the highest point, the body has zero speed but has downward acceleration equal to acceleration due to gravity.
b) False, because velocity is the speed of body in a given direction. When speed is zero, the magnitude of velocity of body is zero, hence velocity is zero.
c) True, when a particle is moving along a strait line with a constant speed, its velocity remains constant with time. Therefore, acceleration ( = Change in velocity/time) is zero.
d) The statement depends upon the choice of instant of time as origin, when the body is moving along a strait line with positive acceleration. The velocity of the body at on instant of time is v = u + at.
The given statement is not correct. If a is positive and μ is negative, at the instant of time taken as origin. Then for all times before the time for which v vanishes, there is slowing down of the particle i.e., The speed of the particle keeps on decreasing with time. It happens when body is projected vertically upwards. However the given statement is true if u is positive, at the instant of time as origin. When the body is moving along a straight line with positive acceleration. The velocity of body at any instant of time t is v = u + at.
The given statement is not correct if a is positive and u is negative, at the instant of time taken as origin. Then for all times before the time for which v vanishes, there is slowing down of the particle i.e., the speed of particle keeps on decreasing with time. It happens when body is projected vertically upwards. However, the given statement is true if u is positive and a is positive, at the instant of time taken as origin. It is so when the body is falling vertically upwards.
![]()
Question 12.
A ball is dropped from a height of 90 m on a floor. At each collision with the floor, the ball loses one tenth of its speed. Plot the speed-time graph of its motion between t = 0 to 12 s.
Solution:
Taking vertical downward motion of ball from a height 90 m We have
u = 0, a = 10 m/s2, S = 90 m, t = ?, v = ?
t = \(\sqrt{\frac{25}{a}}=\sqrt{\frac{2 \times 90}{10}}=3 \sqrt{25}\) = 4.245
V = \(\sqrt{2 a \mathrm{~s}}=\sqrt{2 \times 10 \times 30}=30 \sqrt{2} \mathrm{~m} / \mathrm{s}\)
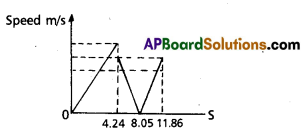
Rebound velocity of ball,
u1 =\(\frac{9}{10} v=\frac{9}{10} \times 30 \sqrt{2}=27 \sqrt{2}\) m/g
Time to reach the highest point is
t1 = \(\frac{u^1}{a}=\frac{27 \sqrt{2}}{10}=2.7 \sqrt{2}\) = 3.81 S
Total time = t + t1 = 4.24 + 3.81 = 8.05 S
The ball will take further 3.1 S to fall back to floor, where its velocity before striking the floor = 2.7\(\sqrt{2}\) m/s.
Time to reach the highest point is,
t1 = \(\frac{u^1}{a}=\frac{27 \sqrt{2}}{10}=2.7 \sqrt{2}\) = 3.81 S
Total time = t + t1 = 4.24 + 3.81 = 8.05 S
The ball will take further 3.81 S fall back to floor, where its velocity before striking the
floor = 2.7\(\sqrt{2}\) m/s.
Velocity of ball after striking the floor
= \(\frac{9}{10}\) \(\sqrt{2}\) = 24.3 \(\sqrt{2}\) m/s.
Total time elapsed before upward motion of ball.
= 8.05 + 3.81 = 11.86 S
Thus the speed – time graph of this motion will be as shown in fig.
Question 13.
Explain clearly, with examples, the distinction between :
a) magnitude of displacement (sometimes called distance) over an interval of time and the total length of path covered by a particle over the same interval:
b) magnitude of average velocity over an interval of time and the average speed over the same interval. [Average speed of a particle over an interval of time is defined as the total path length divided by the time interval]. Show in both (a) and (b) that the second quantity is either greater than or equal to the first. When is the equality sign true ? [For simplicity, consider one-dimensional motion only].
Answer:
a) Magnitude of displacement of a particle in motion for a given time is shortest distance between the initial and final position of the particle in that time, where as the total length of the path covered by particle is actual path traversed by the particle in the given time. If particle goes from A to B and B to C in time t as shown in fig. Then magnitude of displacement = Distance AC.
Total path length = Distance AB + Distance AC
From the above we note that total path length (AB + AC) is greater than magnitude of displacement (AC).
If there is motion of the particle in one dimension i.e., along a straight line, then magnitude of displacement becomes equal to totalpath length transversed by the particle in the given time.
b) Magnitude of average velocity
= \(\frac{\text { Magnitude of displacement }}{\text { Time interval }}\)
= \(\frac{A C}{t}\) and average speed
= \(\frac{\text { Total path length }}{\text { Time interval }}=\frac{(A B+B C)}{t}\)
As, (AB + BC) AC, So average speed is greates than the magnitude of average velocity. If the particle is moving along a straight line, then in a given time the magnitude of displacement is equal to total path length transvered by particle in that time, so average speed is equal to magnitude of average velocity.
![]()
Question 14.
A man walks on a straight road from his home to a market 2.5 km away with a speed of 5 km h-1. Finding the market closed, he instantly turns and walks back home with a speed of 7.5 km h-1. What is the
a) magnitude of average velocity and
b) average speed of the man over the interval of time (i) 0 to 30 min, (ii) 0 to 50 m in, (iii) 0 to 40 min ? [Note: You will appreciate from this exercise why it is better to define average speed as total path length divided by time and not as magnitude of average velocity. You would not like to tell the tired man on his return home that his average speed was zero !]
Solution:
Time taken by man to go from his home to market t1 = \(\frac{\text { Distance }}{\text { Speed }}=\frac{2.5}{5}=\frac{1}{2}\) h
Time taken by man to go from market to his home t2 = \(\frac{2.5}{7.5}=\frac{1}{3}\) h
Total time taken = t1 + t2 = \(\frac{1}{2}+\frac{1}{3}=\frac{5}{6}\)
h = 50 min.
i) 0 to 30 min
a) Average velocity
= \(\frac{\text { Displacement }}{\text { Time }}=\frac{2.5}{1 / 2}\) = 5 km/h
b) Average speed
= \(\frac{\text { Displacement }}{\text { Time }}=\frac{2.5}{1 / 2}\) = 5 km/h
ii) 0 to 50 min
Total distance travelled
= 2.5 + 2.5 = 5 km
Total displacement = zero
a) Average velocity = \(\frac{\text { Displacement }}{\text { Time }}\) = 0
b) Average speed = \(\frac{\text { Distance }}{\text { Time }}=\frac{5}{5 / 6}\) = 6 km/h
iii) 0 to 40 min
Distance moved in 30 min (from home to market) = 2.5 km
Distance moved in 10 min (from market to home) with speed 7.5 km/h = 7.5 × \(\frac{10}{60}\)
= 12.5 km
So displacement = 2.5 – 1.25 = 1.25 km
Distance travelled = 2.5 + 1.25 = 3.75 km
a) Avg velocity = \(\frac{1.25}{(40 / 60)}\) = 1.875 km/h
b) Avg speed = \(\frac{3.75}{(40 / 60)}=\) = 5.625 km/h
Question 15.
In Exercises 3.13and 3.14, we have carefully distinguished between average speed and magnitude of average velocity. No such distinction is necessary when we consider in ‘antaneous speed and magnitude of velocity. The instantaneous speed is alway equal to the magnitude of instantaneous velocity. Why ?
Solution:
Instaneous speed (vins) of the particle at an instant is the first derivative of the distance w.r.to time at that instant of time
i.e., vins = \(\frac{\mathrm{dx}}{\mathrm{dt}}\)
Since in instantaneous speed we take only a small interval of time (dt) during which direction of motion of a body is not supposed to change, here there is no difference between total path length and magnitude of displacement for small interval of time dt. Hence instantaneous speed is always equal to magnitude of instantaneous velocity.
![]()
Question 16.
Look at the graphs (a) to (d) (fig.) carefully and state, with reasons, which of these cannot possibly represent one-dimensional motion of a particle.
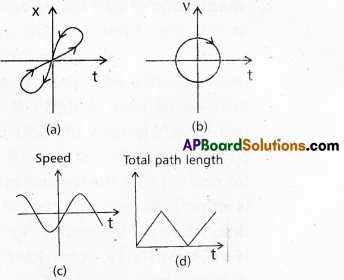
Solution:
a) This graph does not represent one dimensional motion because, at the given instant of time, the particle will have two positions, which is not possible in one dimensional motion.
b) This graph does not represent one dimensional motion because, at the given instant of time, particle will have velocity in positive as well as in negative direction which is not possible in one dimensional motion.
c) It also does not represent one dimensional motion, because this graph tells that the particle can have the negative speed but the speed of the particle can never be negative.
d) It also does not represent one dimensional motion, because this graph tells that the total path length decreases after certain time but total path length of a moving particle can never decrease with time.
Question 17.
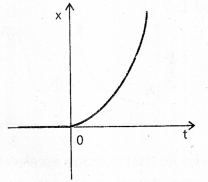
Figure shows the x – t plot of one-dimensional motion of a particle. Is it correct to say from the graph that the particle moves In a straight line for t < 0 and on a parabolic path for t > 0 ? If not, suggest a suitable physical context for this graph.
Solution:
No, because the x – t graph does not represent the trajectory of the path followed by a particle.
From the graph, it is noted that at t = 0, x = 0 context. The above graph can represent the motion of a body falling freely from a tower uncles gravity.
Question 18.
A police van moving on a highway with a speed of 30 km h-1 fires a bullet at a thief’s car speeding away in the same direction with a speed of 192 km h-1. If the muzzle speed of the bullet is 150 ms-1 with what speed does the bullet hit the thief’s car ? (Note : Obtain that speed which is relevant for damaging the thief’s car),
Solution:
Muzzle speed of bullet, υB = 150 m/s = 540 km h-1
Speed of police van, υp = 30 km/h
Speed of theif car, υT = 192 km/h
Since the bullet is sharing the velocity of the police van, its effective velocity is
υB = υB + υP = 540 + 30 = 570 km/h
The speed of bullet w.r.to the theifs car moving in the same direction.
vBT = vB – vT = 570 – 192 = 378 378 km/h
= \(\frac{378 \times 1000}{60 \times 60}\) = 105 m/s
![]()
Question 19.
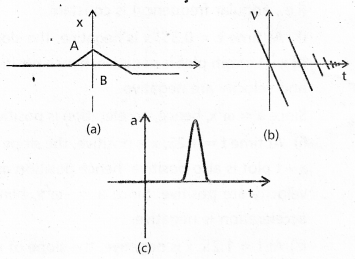
Suggest a suitable physical situation for each of the following graphs (Fig.):
Solution:
In fig(a) : The x – t graph shows that intially x is zero i.e, at rest, then it increases with time, attains a constant value and again reduces to zero with time, then it increases in opposite direction till it again attains a constant value i.e., comes to rest. The similar In fig(b) : The velocity changes sign again and again with passage of time and every time some similar speed is lost. The similar physical situation arises when a ball is thrown up with some velocity, returns back and falls freely on striking the floor, it rebounds with reduced speed each it strikes against the floor.
Question 20.
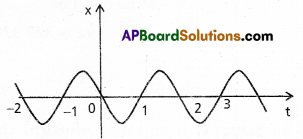
Figure gives the x – t plot of a particle executing one-dimensional simple harmonic motion. (You will learn about this motion in more detail in Chapter 14). Give the signs of position, velocity and acceleration variables of the particle at t = 0.3 s, 1.2 s, -1.2 s.
Solution:
In the S.H.M. acceleration a = ω2x, where co (i.e., angular frequency) is constant.
i) At time t = 0.35, x is negative, the slope of x -1 graph plot is negative, hence position and velocity are negative, Since a =ω2x, hence, acceleration is positive.
ii) At time t = 1.25, x is positive, the slope of x – t plot is also positive hence position and velocity are positive. Since a = -ω2x, hence acceleration is negative.
iii) At t = 1.2S, x is negative, the slope of x – t plot is also negative. But since both x and t are negative here, hence velocity is positive. Finally acceleration ‘a’ is also positive.
Question 21.
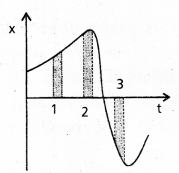
Figure gives the x – t plot of a particle in one-dimensional motion. Three different equal intervals of time are shown. In which interval is the average speed greatest and in which is it the least ? Give the sign of average velocity for each interval.
Solution:
We know that average speed in a small interval of time is equal to slope of x -1 graph in that interval of time. The avg speed is the greatest in the interval 3 because slope is greatest and the average speed is least in interval 2 because slope is last three.
![]()
Question 22.
Figure gives a speed-time graph of a particle in motion along a constant direction. Three equal intervals of time are shown. In which interval is the average acceleration greatest in magnitude ? In which interval is the average speed greatest ? Choosing the positive direction as the constant direction of motion, give the signs of v and a in the three intervals. What are the accelerations at the points A, B, C and D ?
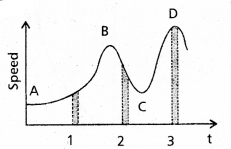
Solution:
We know that average acceleration in a small interval of time is equal to slope of velocity-time graph in that interval. As the slope of v – t graph is maximum in interval 2 as compared to other intervals 1 and 3, hence the magnitude of average acceleration is greatest in interval 2.
The average speed is greatest in interval 3 for obvious reasons.
In interval 1, the speed of v – t graph is positive. Hence acceleration a is positive. The speed u is positive in this interval due to obvious reasons.
In interval 2, the slope of v – t graph is negative, hence acceleration a is negative. The speed u is positive in this interval due to obvious reasons.
In interval 3, the v – t graph is parallel to time axis, therefore acceleration a is zero in this interval but u is positive due to obvious reasons. At points A, B, C and D the v – t graph is parallel to time axis. Therefore acceleration is zero at ail the four points.
Question 23.
A three-wheeler starts from rest, accelerates uniformly with 1 ms-2 on a straight road for 10 s and then moves with uniform velocity. Plot the distance covered by the vehicle during the nth second (n = 1, 2, 3 ) versus n. What do you expect this plot to be during accelerated motion : a straight line or a parabola ?
Solution:
Here u = 0, a = 1 m/s2
Distance covered in n th second is
Dn = u + \(\frac{a}{2}\)(2n-1) = 0 + \(\frac{1}{2}\) (2n – 1) = 0.5 (2n – 1)
Putting n = 1, 2, 3, …………… we can find the value of Dn. The various values of n and corresponding values of Dn are shown below :
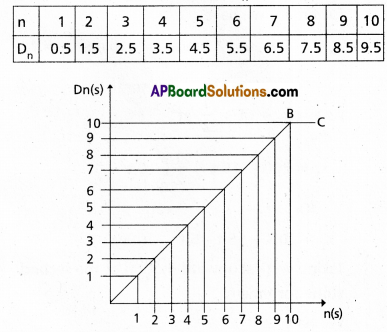
On plotting a graph between Dn and n, we get a st. line AB as shown in fig. From (1) Dn∝n so the graph is a straight line. After 10S the graph is straight line BC parallel to time axis.
Question 24.
A boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can, equal to 49 ms-1. How much time does the ball take to return to his hands ? If the lift starts moving up with a uniform speed of 5 ms-1 and the boy again throws the ball up with the maximum speed he can how long does the ball take to return to his hands ?
Solution:
Taking vertical upward direction as the positive direction of x-axis.
When lift is stationary, consider the motion of the ball going vertically upwards and coming down to the hands of the body. We have
u = 49 m/s, a = 9.8 m/s2, t = ? x – x0 = S = 0
As S = ut + \(\frac{1}{2}\) at2
0 = 49 t + \(\frac{1}{2}\) (-9.8)t2 (Or) 49t = 4.9 t2 (Or)
t = 49/4.9 = 10 sec
When lift starts moving with uniform speed. As the lift starts moving upwards with uniform speed of 5 m/s, there is no change in the relative velocity of the ball w.r.to the boy which remains 49 m/s. Hence even in the case, the ball will return to the boys hand after 10 sec.
![]()
Question 25.
On a long horizontally moving belt a child runs to and fro with a speed 9 km h-1 (with respect to the belt) between his father and mother located 50 m apart on the moving belt. The belt moves with a speed of 4 km h-1. For an observer on a stationary platform outside, what is the
a) speed of the child running in the direction of motion of the belt ?
b) speed of the child running opposite to the direction of motion of the belt ?
c) time taken by the child in (a) and (b) ?
Which of the answer alter if motion is viewed by one of the parents ?
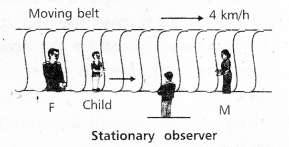
Solution:
Let us consider left to right to be the positive direction of x-axis.
a) Here, the velocity of belt υB = + 4 km/h; Speed of child w.r. to belt υC
= + 9 Km/h = \(\frac{5}{2}\) m/s
Speed of the child w.r.to stationary observer,
υC1 = υC + υB = 9 + 4 = 13 km/h
b) Here, υB = + 4 km/h, υC = -9 km/h
Speed of the child w.r.to stationary observer
υC1 = υC + υB = -9 + 4 = -5 km/h
Here negative sign shows that the child will appears to run in a opposite to the direction f motion of the belt.
c) Distance between the parents S = 540 m Since parents and child are located on the same belt, the speed of the child as observed by stationary observer in either direction (Either from mother to father (or) from father to mother) will be 9 km/h.
Time taken by child in case (a) and (b) is
t = \(\frac{50}{(5 / 2)}\) = 20 S
If motion is observed by one of the parents, answer to case (a) (Or) case (b) will be altered.
It is so because speed of child w.r. to either of mother (or) father is 9 km/h. But answer (c) remains unaltered due to the fact that parents and child are on the same belt and such all are equal affected by the motion of the belt.
Question 26.
Two stones are thrown up simultaneously from the edge of a cliff 200 m high with initial speeds of 15 ms-1 and 30 ms-1. Verify that the graph shown in Fig. correctly represents the time variation of the relative position of the second stone with respect to the first. Neglect air resistance and assume that the stones do not rebound after hitting the ground. Take g = 10 ms-2. Give the equations for the linear and curved parts of the plot.
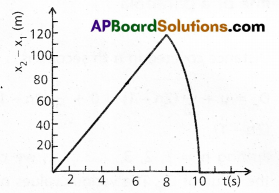
Solution:
Time vertical upward motion of the first tone for time t, we have
x0 = 200 m, u = 15 m/s, a = -10 m/s2, t = t1, x = x1
As x = x0 + ut + \(\frac{1}{2}\) at2
x1 = 200 + 15 t + \(\frac{1}{2}\) (-10)t2 (Or)
x1 = 200 + 15 t – 5 t2 ……………….. (i)
Taking vertical upward motion of the second stone for time t,
We have
x0 = 200 m, u = 30 m/s-1, a = -10 m/s-2, t = t1, x = x2
Then x2 = 200 + 30 t – \(\frac{1}{2}\) × 10 t2
= 200 + 30 t – 5t2
When the first stone hits the ground x1 = 0,
So t2 – 3t – 40 = 0
(Or) (t – 8) (t + 5) = 0 ……………….. (ii)
∴ Either t = 8 S (Or) – 5S
Since t = 0 corresponds to the instant, when the stone was projected. Hence negative time has no meaning in this case. 50 t = 8S. When the second stone hits the ground, x2 = 0.
0 = 200 + 30 t – 5t2 (Or) t2 – 6t – 40 = 0 (Or) (t – 10) (t + 4) = 0
Therefore, either t = 10 s (Or) t = -4s
Since t = -4s is meaningless, So t = 10s
Relative position of second stone w.r.to first is
= x2 – x1 = 15 t …………………….. (ii)
From (i) and (ii)
Since (x2 – x1) and t are linearly related, therefore the graph is a straight line till t = 8s For maximum separation t = 8 S, so maximum separation = 15 × 8 = 120 m After 8 seconds only second tone would be in motion for 2 seconds, so the graph is in accordance with the aquadratic equation x2 = 200 + 30t – 5t2 for the interval of time 8 seconds to 10 seconds.
![]()
Question 27.
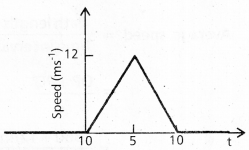
The speed-time graph of a particle moving along a fixed direction is shown in Fig. Obtain the distance traversed by the particle between (a) t = 0 s to 10 s, (b) t = 2s to 6s.
What is the average speed of the particle over the intervals in (a) and (b) ?
Solution:
a) Distance travelled by the particle between 0 to 10s will be
= Area of ∆ OAB, whose base is 10s and height is 12 m/s
= \(\frac{1}{2}\) × 10 × 12 = 60 m 60
Average speed = \(\frac{60}{10}\) = 6mS-1
b) Let s1 and s2 be the distances covered by the particle in the time interval t1 = 2s to 5s and t2 = 5s to 6s, then total distance covered in time interval t = 2s to 6s will be s = s1 + s2 ……………….. (i)
To find s1: let us consider u1 is the velocity of particle after 2 seconds and a1 is the acceleration of the particle during the time interval zero to 5 seconds.
Then u1 = 0, v = 12 m/s,
a = a , a1 and t = 5s
We have a1 = \(\frac{v-u}{t}=\frac{12-0}{5}=\frac{12}{5}\)
= 2.4 m/s2
∴ u1 = υ + a1t = 0 + 2.4 × 2 = 4.8 m/s-1 Thus for the distance travelled by particle in 3 seconds (i.e, time interval 2s to 5s), we have
u1 = 4.8 m/s, t1 = 3s, a1 = 2.4 m/s2, s1 = ?
As s1 = u1t1 + \(\frac{1}{2}\) a1t12
S1 = 4.8 + 3 × \(\frac{1}{2}\) × 2.4 × 32 = 25.2 m
To find s2 : let a2 be the acceleration of the particle during the motion t = 5s to t = 10s
We have a2 = \(\frac{0-12}{10-5}\) = -2.4 m/s2
Taking motion of the particle in time interval t = 5s to t = 6s We have
u1 = 12 m/s-1, a2 = -2.4 m/s2, t2 = 1s, s2 = ?
As s2 = u2t + \(\frac{1}{2}\) a2t22
s2 = 12 × 1 + \(\frac{1}{2}\) (-2.4) 12 = 10.8 m
∴ Total distance travelled s = 25.2 + 10.8
= 36m
Average velocity = \(\frac{36}{6-2}=\frac{36}{4}\) = 9 m/s
Question 28.
The velocity-time graph of a particle in onedimensional motion is shown in Fig.
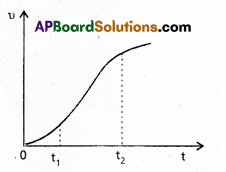
Which of the following formulae are correct for describing the motion of the particle over the time-interval t1 to t2 :
a) x(t2) = x(t1) + v(t1) (t2 – t1) + (\(\frac{1}{2}\)) a(t2 – t1)2
b) v(t2) = v(t1) + a(t2 – t1)
c) vaverage = (x(t2) – x(t1)) / (t2 – t1)
d) vaverage = (v(t2) – v(t1)) / (t2 – t1)
e) x(t2) = x(t2) + Vaverage (t2 – t2) + (\(\frac{1}{2}\)) aaverage (t2 – t1)2
f) x(t2) = x(t1) = area under the y – t curve bounded by the t-axis and the dotted line shown.
Solution:
From the graph we note that the slope is not constant and is not uniform, hence the relations (iii), (iv), (v) are correct.
Textual Examples
Question 1.
A car is moving along a straight line. Say OP Fig. 3.1. It moves from O to P in 1 8s and returns from P to Q in 6.0s. What are the average velocity and average speed of the car in going (a) from O to P? arid (b) from O to P and back to Q?
Solution:

Thus, in this case the average speed is equal to the magnitude of the average velocity.
b) In this case,

![]()
Question 2.
The position of an object moving along x-axis is given by x = a + bt2 where a = 8.5 m, b = 2.5 ms-2 and t is measured in seconds. What is its velocity at t = 0s and t = 2-.0s. What is the average velocity between t = 2.0s and t = 4.0s ?
Solution:
In notation of differential calculus, the velocity is
υ = \(\frac{d x}{d t}=\frac{d}{d t}\)(a + bt2) = 2b t = 5.0 t ms-1
At t = 0s, υ = 0 ms-1 and at t = 2.0s, υ = 10 ms-1
Average velocity = \(\frac{x(4.0)-x(2.0)}{4.0-2.0}\)
= \(\frac{a+16 b-a-4 b}{2.0}\) = 6.0 × b
= 6.0 × 2.5 = 15 ms-1
Question 3.
Obtain equations of motion for cons-tant acceleration using method of calculus.
Answer:
By definition a = \(\frac{\mathrm{dv}}{\mathrm{dt}}\)
dυ = a dt
Integrating both sides
\(\int_{v_0}^v d v=\int_0^t a d t\)
= \(a \int_0^t d t\) (a is constant)
υ – υ0 = at
υ = υ0 + at
Further υ = \(\frac{\mathrm{dx}}{\mathrm{dt}}\)
dx = υ dt
Integrating both sides
\(\int_{x_0}^x d x=\int_0^t v d t=\int_0^t\left(v_0+a t\right) d t\)
x – x0 = υ0 t + \(\frac{1}{2}\) a t2
x = x0 + υ0 t + \(\frac{1}{2}\) a t2
We can write
a = \(\frac{d v}{d t}=\frac{d v}{d x} \frac{d x}{d t}=v \frac{d v}{d x}\)
or, υ dυ = a dx
Integrating both sides,
\(\int_{v_0}^v v d v=\int_{x_0}^x a d x\)
\(\frac{v^2-v_0^2}{2}\) = a(x – x0)
υ2 = υ02 + 2a(x – x0)
The advantage of this method is that it can be used for motion with non-uniform acceleration also.
Now, we shall use these equations to some important cases.
![]()
Question 4.
A ball is thrown vertically upwards with a velocity of 20 ms-1 from the top of a multistorey building. The height of the point from where the ball is thrown is 25.0 m from the ground. [T.S. A.P. Mar. 15]
(a) How high will the ball rise ? and
(b) how long will it be before the ball hits the ground ? Take g = 10 ms-2. (Actual valqp is 9.8 ms-2)
Solution:
a) Let us take the y—axis in the vertically upward direction with zero at the vertically upward direction with zero at the ground, as shown in fig. 3.13.
Now υ0 = + 20 ms-1
a = -g = -10 ms-2,
υ = 0 ms-1
If the ball rises to height y from the point of launch, then using the equation
υ2 + υ02 + 2a(y – y0)
we get
0 = (20)2 + 2(-10) (y – y0)
Solving, we get, (y – y0) = 20 m
b) We can solve this part of the problem in two ways. Note carefully the methods used.
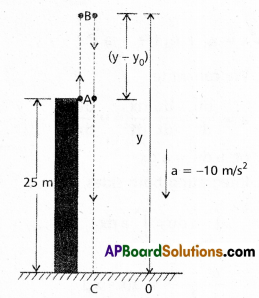
First Method : In the first method, we split the path in two parts : the upward motion (A to B) and the downward motion (B to C) and calculate the corresponding time taken t1 and t2. Since the velocity at B is zero, we have :
υ = υ0 + at
0 = 20 – 10 t1
t1 = 2s
Or,
This is the time in going from A to B. From B, or the point of the maximum height, the ball falls freely under the acceleration due to gravity. The ball is moving in negative y direction. We use equation
y = y0 + υ0t + \(\frac{1}{2}\) at2
We have, y0 = 45 m, y = 0, υ0 = 0,
a = -g = – 10 ms-2
0 = 45 + (\(\frac{1}{2}\)) (-10) t22
Solving, we get t2 = 3s
Therefore, the total time taken by the ball
before it hits the ground = t1 + t2 = 2s + 3s = 5s.
Second method : The total time taken can also be calculated by nothing the coordinates of initial and final positions of the ball with respect to the origin chosen and using equation.
y = y0 + υ0t + \(\frac{1}{2}\) at2
Now y0 = 25 m, y = 0 m
υ0 = 20 ms-1, a = -10 ms-2, t = ?
0 = 25 + 20t + (\(\frac{1}{2}\))(-10)t2
Or, 5t2 -20t – 25 = 0
Solving this quadratic equation for t, we get t = 5s
Question 5.
Free-fall : Discuss the motion of an object under fall. Neglect air resistance.
Solution:
An object released near the surface of the Earth is accelerated downward under the influence of the force of gravity. The magnitude of acceleration due to gravity is represented by g. If air resistance is neglected, the object is said to be in free fall. If the height through which the object falls is small compared to the earth’s radius, g can be taken to be constant, equal to 9.8 ms-2. Free fall is thus a case of motion with uniform acceleration.
We assume that the motion is in y-direction, more correctly in -y-direction because we choose upward direction as positive Since that acceleration due to gravity is always downward, it is in the negative direction and we have
a = – g = -9.8 ms-2
The object is released from rest at y = 0. Therefore, υ0 = 0 and the equations of motion become :
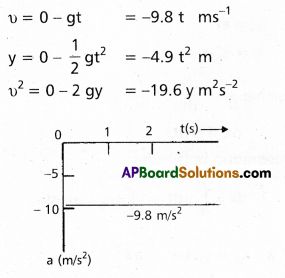
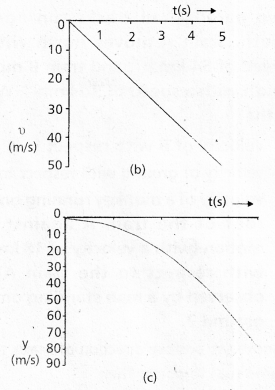
Motion of an object under free fall.
a) Variation of acceleration with time.
b) Variation of velocity with time.
c) Variation of distance with time.
![]()
Question 6.
Galileo’s law of odd numbers : The distances traversed, during equal intervals of time, by a body falling from rest, stand to one another in the same ratio as the odd numbers beginning with unity (namely 1:3:5:7 )n Prove it.
Solution:
We have y = –\(\frac{1}{2}\) gt2 Using this equation, we can calculate the position of the object after different time intervals, 0, τ, τ2, τ3 which are given in second column of table 3.2. If we take (-1/2) gτ2 as y0 – the position coordinate after first time interval τ, then third column gives the positions in the unit of y0. The fourth column gives the distances traversed in successive τs. We find that the distances are in the simple ratio 1: 3 : 5 : 7 : 9 :11 as shown in the last column.
Question 7.
Stopping distance of vehicles : When brakes are applied to a moving vehicle, the distance it travels before stopping is called stopping distance. It is an important factor for road safety and depends on the initial velocity (-υ0) and the braking capacity or deceleration, – a that is caused by the braking. Derive an expression for stopping distance of a vehicle in terms of υ0 and a.
Solution:
Let the distance travelled by the vehicle before it stops be ds. Then, using equation of motion υ2 = υ02 + 2 ax and noting that υ = 0, we have the stopping distance
ds = \(\frac{-v_0^2}{2 a}\)
Thus, the stopping distance is proportional to the square of the initial velocity. Doubling the initial velocity increases the stopping distance by a factor of 4 (for the same deceleration).
For the car of a particular make, the braking distance was found to be 10 m, 20 m, 34 m and 50 m corresponding to velocities of 11, 15,20 and 25 m/s which are nearly consistent with the above formula.
Question 8.
Reaction time : When a situation demands our immediate action. It takes some time before we really respond. Reaction time is the time a person takes to observe, think and act. For example, if a person is driving and suddenly a boy appears on the road, then, the time elapsed before he slams the brakes of the car is the reaction time. Reaction time depends on complexity of the situation and on an individual.
You can measure your reaction time by a simple experiment. Take a ruler and ask your friend to drop it vertically through the gap between your thumb and forefinger (Fig. 3.15). After you catch it, find the distance d travelled by the ruler. In a particular case, d was found to be 21.0 cm. Estimate reaction time.

Solution:
The ruler drops under free fall. Therefore υ0 = 0 and a = -g = -9.8 ms-2. The distance travelled d and the reaction time t, are related by d = –\(\frac{1}{2}\) gtr2 Or tr = \(\sqrt{\frac{2 \mathrm{~d}}{\mathrm{~g}}}\)s.
Given d = 21.0 cm and g = 0.8 ms-2 the reaction time is
tr = \(\sqrt{\frac{2 \times 0.21}{9.8}}\) s ≅ 0.2 s
![]()
Question 9.
Two parallel rail tracks run north- south. Train A moves north with a speed of 54 km h-1 and train B moves south with a speed of 90 kmh-1. What is the
a) velocity of B with respect to A ?
b) velocity of ground with respect to B ?
c) velocity of a monkey running on the roof of the train A against. Its motion (with a velocity of 18 kmh-1 with respect to the train A) as observed by a man standing on the ground ?
Solution:
Choose the positive direction of x-axis to be from south to north. Then,
υA = + 54 km h-1 = 15 ms-1
υB = – 90 km h-1 = -25 ms-1
Relative velocity of B with respect to A = υA – υB = – 40 ms-1, i.e., the train B appears to A to move with a speed of 40 ms-1 from north to souch.
Relative velocity of ground with respect to B = 0 – υB = 25 ms-1
In.(c), let the velocity of the monkey with respect to ground be υM. Relative velocity of the monkey with respect to A,
υMA = υM – υA = – 18 km h– = – 5 mh-1
Therefore, υM = (1 5 – 5)mh-1 = 10 mh-1.