Andhra Pradesh BIEAP AP Inter 1st Year Physics Study Material 6th Lesson Work, Energy and Power Textbook Questions and Answers.
AP Inter 1st Year Physics Study Material 6th Lesson Work, Energy and Power
Very Short Answer Questions
Question 1.
State the conditions under which a force does no work. [T.S. Mar. 15]
Answer:
- When the displacement is zero,
- When the displacement is perpendicular to the direction of the force,
- When the body moves under the action of a conservative force over a closed path.
Question 2.
Define : Work, Power and Energy. State their SI units.
Answer:
Work : The product of magnitude of displacement (S) and component of force (F cos θ) along the direction of displacement is called work, ie., W = \(\vec{F} \cdot \vec{S}\) = F S cos θ.
Unit: Joule
Power : The rate of doing work by a force is called power, i.e., P = \(\frac{\mathrm{W}}{\mathrm{t}}\)
Unit: watt or J/S
Energy : The ability or the capacity to do work is called energy.
Unit: Joule
![]()
Question 3.
State the relation between the kinetic energy and momentum of a body.
Answer:
Kinetic energy (EK) = \(\frac{\mathrm{P}^2}{2 \mathrm{~m}}\); where P = momentum of a body, m = mass of the body
Question 4.
State the sign of work done by a force in the following.
a) Work done by a man in lifting a bucket out of a well by means of a rope tied to the bucket.
b) Work done gravitational force in the above case.
Answer:
a) To lift a bucket out of a well, force equal to the weight of the bucket has to be applied by the man along the vertical in upward direction. Since the displacement is also in upward direction θ = 0 and hence the workdone is positive.
b) The angle between the gravitational force and the displacement is 180°. Therefore workdone by the gravitational force is negative.
Question 5.
State the sign of work done by a force in the following.
a) Work done by friction on a body sliding down an inclined plane.
b) Work done by gravitational force in the above case.
Answer:
a) Friction always acts in a direction, opposite to the direction of motion. Hence work done is negative.
b) The work done is positive.
Question 6.
State the sign of work done by a force in the following.
a) Work done by an applied force on a body moving on a rough horizontal plane with uniform velocity.
b) Work done by the resistive force of air on a vibrating pendulum in bringing it to rest.
Answer:
a) The applied force and the displacement are in same direction. Work is positive.
b) The direction of resistive force is opposite to the direction of motion of the pendulum. Hence work done is negative.
![]()
Question 7.
State if each of the following statements is true or false. Give reasons for your answer.
a) Total energy of a system is always conserved, no matter what internal and external forces on the body are present.
b) The work done by earth’s gravitational force in keeping the moon in its orbit for its one revolution is zero.*
Answer:
- False
- True. Because gravitational force is conservative force.
Question 8.
Which physical quantity remains constant
- in an elastic collision
- in am. inelastic collision ?
Answer:
- In elastic collision : Both momentum and kinetic energy is constant.
- In an inelastic collision : Momentum remains constant.
Question 9.
A body freely falling from a certain height h, after striking a smooth floor rebounds and h rises to a height W2. What is the coefficient of restitution between the floor and the body? [T.S. – Mar.’18]
Answer:
h1 = h, h2 = \(\frac{\mathrm{h}}{2}\)
e = \(\sqrt{\frac{\mathrm{h}_2}{\mathrm{~h}_1}}=\sqrt{\frac{\frac{\mathrm{h}}{2}}{\mathrm{~h}}}=\frac{1}{\sqrt{2}}\)
![]()
Question 10.
What is the total displacement of a freely falling body, after successive rebounds from the same place of ground, before it comes to stop ? Assume that ‘e’ is the coefficient of restitution between the body and the ground.
Answer:
Total distance = \(\frac{h\left(1+e^2\right)}{\left(1-e^2\right)}\), where h is the height through it has fallen and e is the coefficient of restitution.
Short Answer Questions
Question 1.
What is potential energy ? Derive an expression for the gravitational potential energy.
Answer:
Potential energy: Definition : The energy possessed by a body by virtue of its position or state is called potential energy.
e.g. : 1) Energy possessed by water stored in a dam.
2) A stretched rubber card.
Formula for P.E = mgh : The potential energy is measured by the work done in lifting a body through a height ‘h’ against gravitational force. Consider a body of mass m on the body against gravitational force.
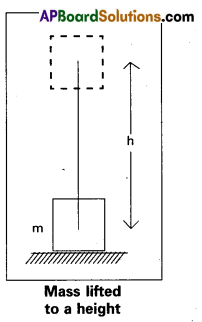
∴ Gravitational force F = Weight of the body
Minimum force needed to lift the body = F in upwards direction
F = mg
Height lifted = h
Work done W = gravitational force × height lifted
W = mgh
This work done is stored as potential energy.
∴ Potential energy P.E = mgh.
Question 2.
A lorry and a car moving with the same momentum are brought to rest by the application of brakes, which provide equal retarding forces. Which of them will come to rest in shorter time ? Which will come to rest in less distance ?
Answer:
F1 = F2 and P1 = P2; W = \(\frac{1}{2}\) mv2 – \(\frac{1}{2}\) mu2; \(\frac{1}{2}\) mu2 = \(\frac{\mathrm{P}^2}{2 \mathrm{~m}}\)
∴ W = F.S = \(\frac{\mathrm{P}^2}{2 \mathrm{~m}}\)
∴ S ∝ \(\frac{1}{m}\)
The heavier body (lorry) comes to rest in shorter time. The lorry will come to rest in less distance.
![]()
Question 3.
Distinguish between conservative and non-conservative forces with one example each.
Answer:
Forces can be classified into two types.
- Conservative force,
- Non conservative force.
1) Conservative force : Conservative forces are the forces under the action of which a body returns to its starting point with same K.F. with which it is projected work done by conservative force is path independent.
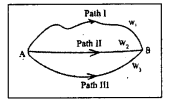
Explanation : If work done along path I, path II, path III are w1, w2, w3 respectively and w1 = w2 = w3 then the force involved in the work is conservative force.
Workdone by a conservative force along a closed path is zero.
Ex. : Gravitational force, electrostatic force, spring force etc.
2) Non-conservative force : Non-conservative force are the forces under the action of which the work done depends upon the path followed and the K.E changes work done by non¬conservative force is path dependent.
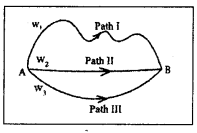
Explanation : If workdone along path I, path II, path III are w1, w2, w3 respectively and w1 ≠ w2 ≠ w3, then the force involved in the work is non conservative. Workdone by a non conservative force along a closed path is not zero.
Ex. : Frictional force, viscous force etc.
Question 4.
Show that in the case of one dimensional elastic collision, the relative velocity of approach of two colliding bodies before collision is equal to the relative velocity of – separation after collision. [T.S. Mar. 18]
Answer:
Consider two spheres (bodies) which have smooth, non-rotating of masses m1 and m2 (m1 > m2) are moving along the straight line joining the centres of mass with initial velocities u1 and u2 (u1 > u2). They undergo head on collision and move along the same line after collision with final velocities of v, and v2. These two bodies exert forces on each other during collision.
Let the collision be elastic, then both momentum and K.E are conserved.
According to law of conservation of linear momentum, Momentum of the system before collision = Momentum of the system after collision.
m1u1 + m2u2 = m1v1 + m1v2
m1(u1 – v1) = m2 (v2 – u2) ……………….. (1)
According to law of conservation of kinetic energy, K.E of the system before collision = K.E of the system after collision.
\(\frac{1}{2}\)m1u12 + \(\frac{1}{2}\)m2u22 = \(\frac{1}{2}\) m1v12 + \(\frac{1}{2}\)m2v22
m1u12 + m2u22 = m1v12 + m2v22
m1(u12 – v12) = m2(v22 – u22) ……………….. (2)
\(\frac{\text { (2) }}{(1)} \Rightarrow \frac{m_1\left(u_1^2-v_1^2\right)}{m_1\left(u_1-v_1\right)}=\frac{m_2\left(v_2^2-u_2^2\right)}{m_2\left(v_2-u_2\right)}\)
\(\frac{\left(u_1-v_1\right)\left(u_1+v_1\right)}{\left(u_1-v_1\right)}=\frac{\left(v_2-u_2\right)\left(v_2+u_2\right)}{\left(v_2-u_2\right)}\)
(u1 – v1) = u2 + v2
u1 – u2 = v2 – v1
Relative velocity of approach from the above equation before collision = Relative velocity of separation after collision.
![]()
Question 5.
Show that two equal masses undergo oblique elastic collision will move at right angles after collision, if the second body initially at rest.
Answer:
Oblique elastic collision : If the centres of mass of the colliding bodies are not initially moving along the line of impact, then the impact is called oblique collision.
Two equal masses undergo oblique elastic collision will move at right angles after collision, if the second body initially at rest:
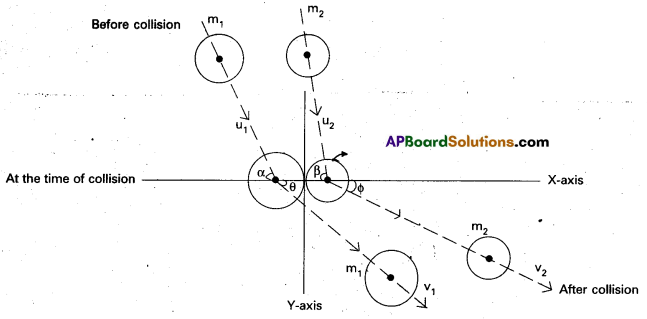
Consider two smooth and perfectly elastic spheres of masses m1 and m2. Let u1 and u2 be their initial velocities before collission. Let v1 and v2 be their final velocities after collision, (α, β) and (θ, Φ) are the angles, the directions of motion make with the line of impact before collision and after collision.
Since the spheres are smooth, there is no (impulse) change of velocities perpendicular to the line of impact. Hence the resolved parts of velocity of the two spheres in the direction perpendicular to the line of impact remain unchanged.
∴ v1 sinθ = u1 sinα ……………………. (1)
and v2 sinΦ = u2 sin β …………………. (2)
According to the principle of conservation of momentum, the sum of the moment of the two spheres along the line of impact before collision and after collision are equal.
∴ m1u1 cosα + m2u2 cosβ = m1v1 cosθ + m2v2 cosΦ ……………… (3)
⇒ m1(u1 cosα – v, cosθ) = m2 (v2 cosΦ – u2 cosβ) ……………….. (4)
According to the principle of conservation of kinetic energy, the sum of the K.E along the line of impart before and after are equal.
⇒ \(\frac{1}{2}\) m1 (u1cosα)2 + \(\frac{1}{2}\)m2 (u2cosβ)2 = \(\frac{1}{2}\) m1 (v1cosθ)2 + \(\frac{1}{2}\)m2(v2cos126,Φ)2
⇒ m1 [(u1cosα)2 – (v1cosθ)2 ] = m2 [(v2cosΦ)2 – (u2cosβ)2] …………….. (5)
\(\frac{(5)}{(4)}\) ⇒ u1 cosα + v1 cosθ = v2 cosΦ + u2 cosβ
v1cosθ = v2 cosΦ + u2 cosβ – u1 cosα ……………… (6)
and v2 cosΦ = v1 cosθ + u1 cosα – u2 cosβ ……………….. (7)
sub. equation (7) in equation (3), we get
v1 cosθ = \(\left(\frac{m_1-m_2}{m_1+m_2}\right)\) u1 cosα + \(\left(\frac{2 m_u u_2}{m_1+m_2}\right)\) cosβ ……………… (8)
Sub-equation (6) in equation (3), we get
and v2 cosΦ = \(\left(\frac{m_2-m_1}{m_1+m_2}\right)\) u2 cosβ + \(\left(\frac{2 m_1 u_1}{m_1+m_2}\right)\) cosα ………………. (9)
If u2 = 0 and m1 = m2 then equation (2), we get Φ = 0 and from equation (8), θ = 90°. This means that if a sphere of mass ‘m’ collides obliquely on another perfectly elastic sphere of the same mass at rest, the directions of motions of the spheres after impact will be at right angles.
Question 6.
Derive an expression for the height attained by a freely falling body after ‘n’ number of rebounds from the floor.
Answer:
Consider a small sphere fall freely at a height ‘h’ onto the floor. It strikes the floor with a velocity of ‘u’
So that u1 = \(\sqrt{2 g h}\) …………….. (1)
At the time of collision between the sphere and the floor, the initial and final velocities of floor are zero i.e., u2 = 0 and v2 = 0
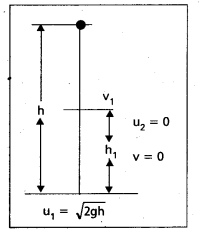
Let ‘v1‘ be the final velocity of the sphere after the first collision.
∴ e = \(\frac{v_2-v_1}{u_1-u_2}=\frac{0-v_1}{\sqrt{2 g h}-0}=\frac{-v_1}{\sqrt{2 g h}}\)
∴ v1 = -e\(\sqrt{2 g h}\) ……………… (2)
(-) indicates that the sphere rebounds
∴ The height (h1) attained by the sphere after first rebound is
h1 = \(\frac{v_1^2}{2 g}=\frac{(e \sqrt{2 g h})^2}{2 g}\) = e2h
h1 = (e2)1 h ………………… (3)
Similarly we can that velocity attained by the sphere after second rebound.
v2 = -e2 \(\sqrt{2 g h}\) …………………. (4)
and maximum height attained by the sphere after second rebound
h2 = (e2)2 h ………………… (5)
From the (2) and (4) equations
velocity of the sphere rebounds after ‘n’ collisions
vn = en \(\sqrt{2 g h}\)
From the (3) and (5) equations, maximum height attained by the sphere after n rebounds hn = (e2)n h
![]()
Question 7.
Explain the law of conservation of energy.
Answer:
The total mechanical energy of the system is conserved if the forces doing work on it are conservative. If some of the forces involved are non-conservative, part of the mechanical energy may get transformed into other forms such as heat, light and sound. However, the total energy of an isolated system does not change, as long as one accounts for all forms of energy. Energy may be transformed from one form to another but the total energy of an isolated system remains constant. Energy can neither be created, nor destroyed.
Since the universe as a whole may be viewed as an isolated system, the total energy of the universe is constant. If one part of the universe looses energy, another part must gain an equal amount of energy.
Long Answer Questions
Question 1.
Develop the notions of work and kinetic energy and show that it leads to work energy theorem. [A.P. Mar. 17; T.S. Mar. 15, 14]
Answer:
Statement : The change in kinetic energy of a particle is equal to the workdone on it by the net force, i.e., kf – ki = W
Proof : Consider a particle of mass ‘m’ is moving with initial speed ‘u’ to final speed ‘v’. Let ‘a’ be its constant acceleration and S be its distance traversed. The kinematic relation is given by
v2 – u2 = 2as ………………. (1)
Multiplying both sides by \(\frac{\mathrm{m}}{2}\), we have 11
\(\frac{1}{2}\) mv2 – \(\frac{1}{2}\) mu2 mas = FS …………….. (2)
Where the last step follows from Newton’s second law.
We can generalise Equation (1) to three dimensions by employing vectors
v2 – u2 = 2 \(\overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{d}}\)
Once again multiplying both sides by \(\frac{\mathrm{m}}{2}\), we obtain
\(\frac{1}{2}\) mv2 – \(\frac{1}{2}\) mu2 = m \(\overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{d}}\) – \(\overrightarrow{\mathrm{F}} \cdot \overrightarrow{\mathrm{d}}\) …………………. (3)
The above equation provides a motivation for the definitions of work and kinetec energy.
In equation (3), \(\frac{1}{2}\) mv2 – \(\frac{1}{2}\) mu2 = kf – ki
Where ki, kf are initial and final kinetic energies and \(\overrightarrow{\mathrm{F}} \cdot \overrightarrow{\mathrm{d}}\) = W, where W refers workdone by a force on the body over a certain displacement.
kf – ki = W ……………….. (4)
Equation (4) is also a special case of the work-energy (WE) theorem.
![]()
Question 2.
What are collisions ? Explain the possible types of collisions ? Develop the theory of one dimensional elastic collision. [T.S. Mar. 18]
Answer:
Collisions : A strong interactions between bodies that occurs for a very short interval during which redistribution of momenta occur ignoring the effect of other forces are called collisions.
Collisions are of two types :
i) Elastic collision : The collision in which both momentum and kinetic energy is constant is called elastic collision.
ii) Inelastic collision: The collision in which momentum remains constant but not kinetic energy is called Inelastic collision.
One dimensional elastic collision : Consider two spheres (bodies) which have smooth, non-rotating of masses m1 and m2 (m1 > m2) are moving along the straight line joining their centres of mass with initial velocities u1and u2 (u1 > u2). They undergo head on collision and move along the same line after collision with final velocities v1 and v2. These two bodies exert forces on each other during collision.
Hence both momentum and kinetic energy are conserved. According to law of conservation of linear momentum.
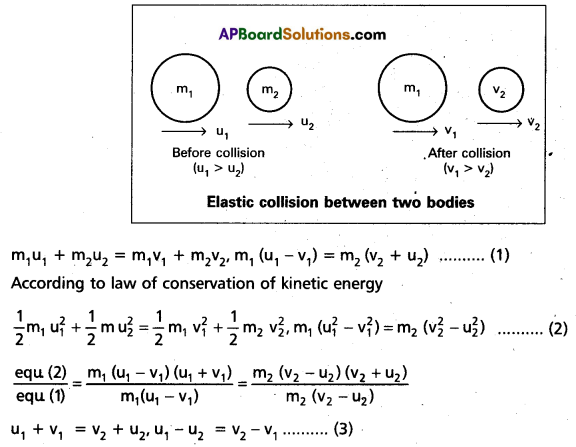
From the above equation, in one dimensional elastic collision, the relative velocity of approach before collision is equal to the relative velocity of separation after collision.
From equation (3) u1 – u2 = v2 – v1, v2 = u1 – u2 + v1 ………………… (4)
Sub equation (4) in equation (1) we get
m1 (u1 – v1) = m2 (u1 – u2 + v1 – u2), m1 u1 – m1v1 = m2 u1 – m2 u2 + m2 v1 – m2 u2
m1 u1 – m2 u1 + 2 m2 u2 = m1 v1 + m2 v1 (m1 – m2) u1 + 2 m2 u2 = (m1 + m2) u1
vi = \(\left(\frac{m_1-m_2}{m_1+m_2}\right) u_1+\left(\frac{2 m_2}{m_1+m_2}\right) u_2\) ………………… (5)
From the equation (4), v1 = v2 – u1 + u2
Sub. this value in equation (1) we get
m1 (u1 – v2 + u1 – u2) = m2 (v2 – u2), m1 u1 – m1 v2 + m1 u1 – m1 u2 = m2 v2 – m2 u2
2m1 u1 + u2 (m2 – m1) = (m2 + m2)v2
v2 = \(\frac{2 m_1 u_1}{\left(m_1+m_2\right)}+\frac{\left(m_2-m_1\right)}{\left(m_1+m_2\right)}\) u2
![]()
Question 3.
State and prove law of conservation of energy in case of a freely falling body. [AP – Mar. ’18, ’16, ’15, ’13; TS – Mar. ’17, ’16]
Answer:
Statement: “Energy can neither be created nor destroyed. But it can be converted from one form to another form. The total energy of a closed system always remains constant”. This law is called law of conservation of energy.
Proof : In case of freely falling body : A body of mass’m’ is dropped or freely falling at a height ‘H‘ from the ground. The total mechanical energy of the body E = K + U.
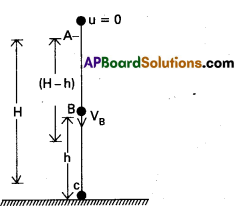
Where k = kinetic energy; U = potential energy.
Suppose A, B and C are the points at heights H, h and ground respectively.
At ‘A’ : At the highest point, velocity u = 0
Kinetic energy K.E. = \(\frac{1}{2}\) mu2 = 0
Potential energy P.E. = mgH
Total mechanical energy of the body = EA = P.E. + K.E. = mgH + 0
∴ EA = mgH ………………. (1)
At ‘B’: When the body falls from A to B, which is at a height ‘h’ from the ground. The velocity of the body at ‘B’ is VB.
At ‘B’ the body possesses both P.E and K.E
S = H – h
u = 0
a = g
v = vB = ?
vB2 – u2 = 2as
a = g
v = vB = ?
vA2 – 0 = 2g (H – h)
VB = 2g(H – h)
Kinetic energy of the body (K) = \(\frac{1}{2}\) mvB2 = \(\frac{1}{2}\) m 2g(H – h)
K = mg (H – h)
Potential energy (u) = mgh
∴ Total mechanical energy at B = k + u
EB = mg (H – h) + mgH
EB = mgh ……………… (2)
At ‘C’ : When the body reaches the point ‘c’ on the ground. The velocity of the body at ‘c is ‘vc’ can be found by using v2 – u2 = 2as equation.
S = H
u = 0
a = g
v = vc = ?
vc2 – 0 = 2gH
vc2 = 2gH
vc = \(\sqrt{2 \mathrm{gH}}\)
Kinetic energy of the body (k) = \(\frac{1}{2}\) mvc2
= \(\frac{1}{2}\) m 2gH = mgH
Potential energy (u) = 0
Total energy at c = k + u
∴ EC = mgH ………………. (3)
From the above three equations (1), (2) and (3), the mechanical energy of the body remains constant under the action of gravitational force. Hence, law of conservation of energy is proved incase of freely falling body.
Problems
Question 1.
A test tube of mass 10 grams closed with a cork of mass 1 gram contains some ether. When the test tube is heated the cork flies out under the pressure of the ether gas. The test tube is suspended horizontally by a weight less rigid bar of length 5cm. What is the minimum velocity with which the cork should fly out of the tube, so that test tube describing a full vertical circle about the point O. Neglect the mass of ether.
Answer:
Mass of test tube M = 10g; Mass of ether m = 1g ;
Length of rigid bar = radius of circle (r) = 5cm

∴ r = 5 × 10-2 m, g = 10 ms2
[∴ action = – reaction]
Given the minimum velocity of cork flies out (= -v) (v) = The minimum velocity of test tube right
v = \(\sqrt{5 r g}=\sqrt{5 \times 5 \times 10^{-2} \times 10}\)
= 5 × \(\sqrt{10^{-1}}\) m/s
![]()
Question 2.
A machine gun fires 360 bullets per minute and each bullet travels with a velocity of 600 ms-1. If the mass of each bullet is 5 gm, find the power of the machine gun ? [A.P. – Mar. ’18, ’16; Mar. ’13]
Answer:
Here n = 360; t = 60 sec; V = 600 ms-1; m = 5g = 5 × 10-3 kg; Power,
P = \(\frac{\text { K.E of n} \text { bullets }}{t}=\frac{\frac{1}{2} \mathrm{mnV}^2}{t}\)
= \(\frac{\frac{1}{2} \times 5 \times 10^{-3} \times 360 \times 600 \times 600}{60}\)
∴ P = 5400, W = 5.4 KW.
Question 3.
Find the useful power used in pumping 3425 m3 of water per hour from a well 8 m deep to the surface, supposing 40% of the horse power during pumping is wasted. What is the horse power of the engine ?
Answer:
Here V = 3425 m3; d = 103 kg m-3; h = 8m;
g = 9.8ms-2; t = 1 hour = 60 × 60s

166.6 HP [1 hp = 746 Watt]
Question 4.
A pump is required to lift 600 kg of water per minute from a well 25 m deep and to eject it with a speed of 50 ms-1. Calculate the power required to perform the above task ? [Mar. 16 (TS), A.P (Mar. ’15)
Answer:
Here m = 600kg; h = 25m; V = 50ms-1; t = 60s;
Power of the motor,
P = \(\frac{\mathrm{mgh}+\frac{1}{2} m \mathrm{~V}^2}{\mathrm{t}}=\frac{\mathrm{m}\left(\mathrm{gh}+\frac{\mathrm{V}^2}{2}\right)}{\mathrm{t}}\)
= \(\frac{600}{60}\left(9.8 \times 25+\frac{50 \times 50}{2}\right)\)
= 10 (245 + 1250) = 14950 = 14.95 KW.
![]()
Question 5.
A block of mass 5 kg initially at rest at the origin is acted on by a force along the X-positive direction represented by F = (20 + 5x)N. Calculate the work done by the force during the displacement of the block from x = 0 to x = 4 m.
Answer:
Given m = 5kg;
F = (20 + 5x)
W = \(\int_{x=0}^{x=4} F d x\)
= \(\int_0^4(20+5 x) d x\)
= \([20 x]_0^4+\left[5 \frac{x^2}{2}\right]_0^4\)
= 20 × 4 + 5 × \(\frac{16}{2}\)
= 120 J.
Question 6.
A block of mass 2.5 kg is sliding down a smooth inclined plane as shown. The spring arranged near the bottom of the inclined plane has a force constant 600 N/m. Find the compression in the spring at the moment the velocity of the block is maximum?
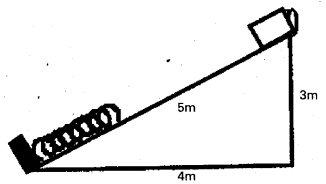
Answer:
Here m = 2.5 kg
µ = 0; K = 600 N/m
Let ‘x’ be the compression of the spring.
According to Newton’s third law, we have
Force due to block on spring
FB = – Restoring force of spring (FR)
In magnitude FB = FR = mg sinθ = Kx
2.5 × 10 × \(\frac{3}{5}\) = 600 × x
⇒ x = \(\frac{15}{600}\)
= 0.025 cm.
Question 7.
A force F = –\(\frac{K}{x^2}\)(x ≠ 0)acts on a particle along the X-axis. Find the work done by the force in displacing the particle from x = C +a to x = +2a. Take K as a positive constant.
Answer:
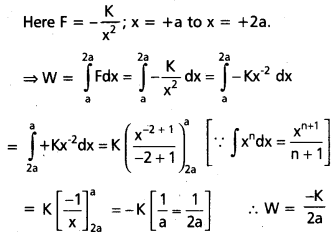
![]()
Question 8.
A force F acting on a particle varies with the position x as shown in the graph. Find the work done by the force in displacing the particle from x = -a to x = +2a.
Answer:
Average force, F = \(\frac{+2 b-b}{2}=\frac{b}{2}\)
⇒ x = -a to x = 2a
W = \(\int_{-a}^{+2 a} F d x=F[x]_a^{+2}=\frac{b}{2}[2 a-(-a)]=\frac{3 a b}{2}\)
Question 9.
From a height of 20m above a horizontal floor, a ball is thrown down with initial velocity 20 m/s. After striking the floor, the ball bounces to the same height from which it was thrown. Find the coefficient of restitution for the collision between the ball and the floor.
Answer:
Here u = 20 mIs; s = h = 20m; g = 10m/s2;
v = u1
using, v2 – u2 = 2as
u12 = 202 = 2 × 10 × 20
u12 = 202 + 400 = 800
∴ u1 = \(\sqrt{800}\)
And v1 = \(\sqrt{2 \mathrm{gh}}=\sqrt{2 \times 10 \times 20}=\sqrt{400}\)
Since floor is at rest u2 = 0; v2 = 0
e = \(\frac{v_2-v_1}{u_1-u_2}=\frac{0-\sqrt{400}}{800-0}=-\frac{1}{\sqrt{2}}\)
∴ e = \(\frac{1}{\sqrt{2}}\) […. -ve sign indicates, if rebounds]
![]()
Question 10.
A Ball falls from a height of 10 m on to a hard horizontal floor and repeatedly bounces. If the coefficient of restitution is \(\frac{1}{\sqrt{2}}\). What is the total distance travelled by the ball before it ceases to rebound ?
Solution:
Given h = 10m; e = \(\frac{1}{\sqrt{2}}\)
d = h\(\left[\frac{1+\mathrm{e}^2}{1-\mathrm{e}^2}\right]=10\left[\frac{1+\frac{1}{2}}{1-\frac{1}{2}}\right]=10\left[\frac{\left(\frac{3}{2}\right)}{1 / 2}\right]\)
∴ d = 30 m
Additional Problems
Question 1.
The sign of work done by a force on a body is important to understand. State carefully if the following quantities are positive or negative:
a) Work done by a man ¡n lifting a bucket out of a well by means of a rope tied to the bucket.
b) Work done by gravitational force in the above case,
c) Work done by friction on a body sliding down an inclined plane,
d) Work done by an applied force on a body moving on a rough horizontal plane with uniform velocity.
e) Work done by the resistive force of air on a vibrating pendulum in bringing it to rest.
Answer:
Workdone W = \(\vec{F} \cdot \vec{S}\) = FS cosθ where θ is smaller angle between force j and displacement \(\vec{S}\).
a) To lift the bucket, force equal to weight of b
b) The bucket moves in a direction opposite to the gravitational force which acts vertically downwards.
θ = 180°
W = FS cos 180° = -FS. It is negative
c) Friction always opposite the relative motion.
∴ θ = 180°, W = FS cos 180° = -FS. It is negative.
d) As the body moves along the direction of applied force θ = 0, W = FS cos 0° = FS. It is positive.
e) The direction of resistive face is opposite to the direction of motion of the bob i.e. θ = 180°. Hence workdone, in this case, is negative.
![]()
Question 2.
A body of mass 2kg initially at rest moves under the action of an applied horizontal force of 7 N on a table with coefficient of kinetic friction = 0.1. Compute the
a) Work done by the applied force in 10s,
b) Work done by friction in 10s,
c) Work done by the net force on the body in 10s.
d) Change in kinetic energy of the body in 10s. and interpret your results.
Answer:
Here, m = 2kg, u = 0, F = 7N; µ = 0.1,
W = 2, t = 10s
Acceleration produced by applied force;
a = –\(\frac{F}{m}=\frac{7}{2}\) = 3.5 m/s2
force of friction, f = µR = µmg = 0.1 × 2 × 9.8 = 1.96 N
Retardation produced by friction
a2 = –\(\frac{F}{m}=\frac{-1.96}{2}\) = 0.98 m/s2
Net acceleration with which body moves,
a = a1 + a2
= 3.5 – 0.98 = 2.52m/s2
Distance moved by the body in 10 second from
S = Ut + \(\frac{1}{2}\) at2
= 0 + \(\frac{1}{2}\) × 2.52 × (10)2 = 126m.
a) Workdone by the applied force = F × S
W1 = 7 × 126 = 882J
b) Workdone by force of friction W2
= -f × s = -1.96 × 126 = 246.9J
c) Workdone by the net force W3 = Net force × distance
= (F – f)s = (7 – 1.96)126 = 635 J.
d) From v = u + at
v = 0 + 2.52 × 10 = 25.2 mS-1
Final K.E = \(\frac{1}{2}\) mv2 = \(\frac{1}{2}\) × 2 × (25.2)2
= 635J
Initial K.E = \(\frac{1}{2}\)mu2 = 0
∴ Change in K.E = 635 – 0 = 635 J.
This shows that change in K.E of the body is equal to workdone by the net force on the body.
Question 3.
Given in Fig. are examples of some potential energy functions in one dimension. The total energy of the particle is indicated by a cross on the ordinate axis. In each case, specify the regions, if any, in which the particle cannot be found for the given energy. Also, indicate the minimum total energy the particle must have in each case. Think of simple physical contexts for which these potential energy shapes are relevant.
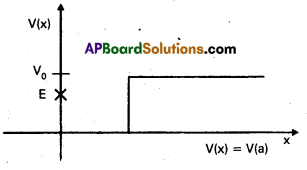
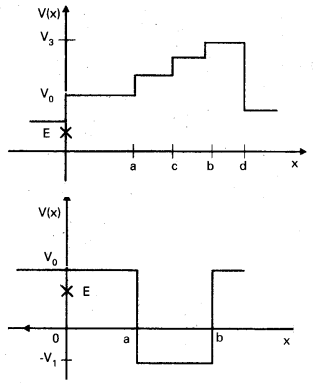
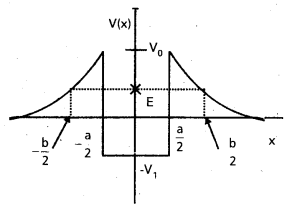
Answer:
We know that total energy E = P.E + K.E (or) K.E = E – P.E and K.E can never be negative. The object cannot exist in the region where its K.E would become negative.
- For x > a, P.E (v0) > E
∴ K.E becomes negative. Hence the object cannot exist in the region x > a. - For x < a and x > b, P.E (v0) > E
∴ K.E becomes negative. Hence the object cannot be present in the region x < a and x > b. - Object cannot exist in any region because P.E (v0) > E in every region.
- On the same basis, the object cannot exist in the region -b/2 < x < – a/2 and a/2 < x < b/2.
![]()
Question 4.
To potential energy function for a particle executing linear simple harmonic motion is given by V(x) = kx2/ 2, where k is the force constant of the oscillator. For k= 0.5 N m-1, the graph of V(x) versus x is shown in Fig. Show that a particle of total energy 1 J moving under this potential must ‘turn back’ when it reaches x = ± 2m
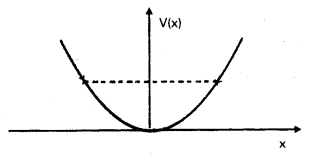
Answer:
At any instant, the total energy of an oscillator is the sum of K.E and P.E i.e.
E = K.E + P.E, E = \(\frac{1}{2}\) mu2 + \(\frac{1}{2}\) kx2
The particles turns back at the instant, when its velocity becomes zero i.e. u = 0.
∴ E = 0 + \(\frac{1}{2}\) kx2 as E = 1 Joule and K = \(\frac{1}{2}\) N/m
∴ 1 = \(\frac{1}{2}\) × \(\frac{1}{2}\) x2 (or) x2 = 4, x = ± 2m.
Question 5.
Answer the following :
a) The casing of a rocket in flight burns up due to friction. At whose expense is the heat energy required for burning obtained ? The rocket or the atmosphere ?
b) Comets move around the sun in highly elliptical orbits. The gravitational force on the comet due to the sun is not normal to the comet’s velocity in general. Yet the work done by the gravitational force over every complete orbit of the comet is zero. Why ?
c) An artificial satellite orbiting the earth in very thin atmosphere loses its energy gradually due to dissipation against atmospheric resistance, however small. Why then does its speed increase progressively as it comes closer and closer to the earth ?
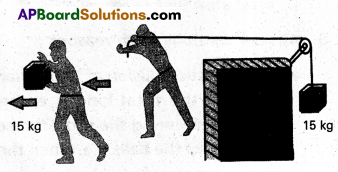
d) In fig. (i) the man walks 2 m carrying a mass of 15 kg on his hands. In Fig. (ii), he walks the same distance pulling the rope behind him. The rope goes over a pulley, and a mass of 15 kg hangs at its other end. In which case is the work done greater ?
Answer:
a) The total energy of a rocket in a flight depends on its mass i.e. P.E + K.E = mgh + \(\frac{1}{2}\) mv2. When the casing burns up, its mass decreases. The total energy of the rocket decreases Hence heat energy required for burning is obtained from the rocket itself and not from the atmosphere.
b) This is because gravitational force is a conservative force. Work done by the gravitational force of the sun over a closed path in every complete orbit of the comet is zero.
c) When the artificial satellite orbiting the earth comes closer and closer to the earth, its potential energy decreases as sum of potential energy and kinetic energy is constant, therefore K.E of satellite and hence its velocity goes on increasing. However total energy of satellite decreases a little on account of dissipation against atmospheric resistance.
d) In fig. (a), force is applied on the mass, by the man in vertically upward direction but distance is moved along the horizontal.
∴ θ = 90°, W = FS cos 90° = zero.
In fig. (b), force is applied along the horizontal and the distance moved is also along the horizontal. Therefore v = 0°.
W = FS cosθ = mg × S cos0°
W = 15 × 9.8 × 2 × 1 = 294 Joule.
workdone in 2nd case is greater.
![]()
Question 6.
Underline the correct alternative :
a) When a conservative force does positive work on a body, the potential energy of the body increases / decreases / remains unaltered.
b) Work done by a body against friction always .results in a loss of its kinetic / potential energy.
c) The rate of change of total momentum of a many-particle system is proportional to the external force / sum of the internal forces on the system.
d) In an inelastic collision of two bodies, the quantities which do not change after the collision are the total kinetic energy/total linear mometum. total energy of the system of two bodies.
Answer:
a) Potential energy of the body decreases. The conservative force does positive work on a body, when it displaces the body in the direction of force. The body, therefore, approaches the center of force, decreasing x. Hence P.E decreases.
b) Workdone by a body against friction at the expense of its kinetic energy. Hence K.E of the body decreases.
c) Internal forces cannot change the total (or) net momentum of a system. Hence the rate of change of total momentum of many particle system is proportional to the external force on the system.
d) In an inelastic collision of two bodies, the quantities which do not change after the collision are total linear momentum and total energy of the system of two bodies. The total K.E changes as some energy appears in other forms.
Question 7.
State if each of the following statements is true or false. Give reasons for your answer.
a) In an elastic collision of two bodies, the momentum and energy of each body is conserved.
b) Total energy of a system is always conserved, no matter what internal and external forces on the body are present.
c) Work done in the motion of a body over a closed loop is zero for every force in nature.
d) In an inelastic collision/the final kinetic energy is always less than the initial kinetic energy of the system.
Answer:
a) False. The total momentum and total energy of the system are conserved and not of each body.
b) False. The external forces on the body may change the total energy of the body.
c) False. Work done in the motion of a body over a closed loop is zero only the body is moving under the action of conservative forces (like gravitational (or) electrostatic faces).
It is not zero when the forces are non conservative, e.g. frictional forces etc.
d) True, because in an inelastic collision, some kinetic energy usually changes into some other form of energy.
Question 8.
Answer carefully, with reasons ;
a) In an elastic collision of two billiard balls, is the total kinetic energy conserved during the short time of collision of the balls (i.e. when they are in contact) ?
b) Is the total linear momentum conserved during the short time of an elastic collision of two balls ?
c) What are the answer to (a) and (b) for an inelastic collision ?
d) If the potential energy of two billiard balls depends only on the separation distance between their centres, is the collision elastic or inelastic ? (Note, we are talking here of potential energy corresponding to the force during collision, not gravitational potential energy).
Answer:
a) No, K.E is not conserved during the given elastic collision. K.E. before and after collision is the same. Infact during collision, K.E of the balls gets converted into potential energy.
b) Yes, the total linear momentum is conserved during the short time of an elastic collision of two balls.
c) In an in elastic collision, total K.E is not conserved during collision.
d) The collision is elastic, because the forces involved are conservative.
![]()
Question 9.
A body is initially at rest. It undergoes one-dimensional motion with constant acceleration. The power delivered to it at time t is proportional to
i) t1/2
ii) t
iii) t3/2
iv) t2
Answer:
From v – u + at, v = 0 + at = at
As power, p = F × v = (ma) × at = ma2t
As m and a are constants, therefore, p ∝ t.
Question 10.
A body is moving unidirectionally under the influence of a source of constant power. Its displacement in time t is proportional to
i) t1/2
ii) t
iii) t3/2
iv) t2
Answer:
As power, P = force × velocity
∴ P = [MLT-2] [LT-1] = [mL2 T-3]
As P = [mL-2 T-3] = constant
∴ L2 T-3 = constant
∴ L2 ∝ T3 (or) L ∝ T3/2
(or) \(\frac{\mathrm{L}^2}{\mathrm{~T}^3}\) = constant
Question 11.
A body constrained to move along the z-axis of a coordinate system is subject to a constant force F given by F = \(-\hat{\mathrm{i}}+2 \hat{\mathrm{j}}+2 \hat{\mathrm{k}}\) N where \(\hat{i}, \hat{j}, \hat{k}\) are unit vectors along the x-, y- and z-axis of the system respectively. What is the work done by this force in moving the body a distance of 4 m along the z-axis ?
Answer:
Here, F = \(-\hat{\mathrm{i}}+2 \hat{\mathrm{j}}+2 \hat{\mathrm{k}}\)N
\(\overrightarrow{\mathrm{S}}=4 \hat{\mathrm{k}}\) (∵ 4m distance is along z-axis)
W = 2; As W = \(\overrightarrow{\mathrm{F}} \cdot \overrightarrow{\mathrm{S}}\)
∴ W = \((-\hat{\mathrm{i}}+2 \hat{\mathrm{j}}+3 \hat{\mathrm{k}}) \cdot(4 \hat{\mathrm{k}})=12 \hat{\mathrm{k}} \cdot \hat{\mathrm{k}}\) = 12J.
![]()
Question 12.
An electron and a proton are detected in a cosmic ray experiment, the first with kinetic energy 10 keV and the second With 100 keV. Which is faster, the electron or the proton ? Obtain the ratio of their speeds, (electron mass = 9.11 × 10-31 kg, proton mass = 1.67 × 10-27 kg, 1 eV = 1.60 × 10-19 J).
Answer:
E1 = \(\frac{1}{2}\) meve2 = 10 × 1.6 × 10-16 ……………… (i)
E2 = \(\frac{1}{2}\) mpvp2 = 100 × 1.6 × 10-16 ……………… (ii)
Divide (i) by (ii) \(\frac{m_v v_v^2}{m_p v_p^2}=\frac{1}{10}\)
\(\frac{v_{\mathrm{e}}}{v_\rho}=\sqrt{\frac{1}{10}} \frac{m \rho}{m_e}\)
= \(\sqrt{\frac{1.67 \times 10^{-27}}{10 \times 9.11 \times 10^{-31}}}=10^2 \sqrt{\frac{1.67}{91.1}}\) = 13.53
Question 13.
A rain drop of radius 2 mm falls from a height of 500 m above the ground. It falls with decreasing acceleration (due to viscous resistance of the air) until at half its original height, it .attains its maximum (terminal) speed and moves with uniform speed thereafter. What is the work done by the gravita-tional force on the drop in the first and second half of its journey ? What is the work done by the resistive force in the entire journey if its speed on reaching the ground is 10 ms-1 ?
Answer:
Here, r = 2mm = 2 × 10-3m
Distance moved in each half of journey,
s = \(\frac{500}{2}\) = 250 m
Density of water, ρ = 103 kg/m3
Mass of rain drop
= Volume of drop × Density
m = \(\frac{4}{3}\)πr3 × ρ = \(\frac{4}{3}\) × \(\frac{22}{7}\) (2 × 10-3)3 × 103
= 3.35 × 10-5 kg
w = mg × s = 3.35 × 10-5 × 9.8 × 250 = 0.082J
It should be clearly understood that whether the drop moves with decreasing acceleration (or) with uniform speed, work done by the gravitational force on the drop remains the same.
If there were no resistive forces, energy of drop on reaching the ground.
E1 = mgh = 3.35 × 10-5 × 9.8 × 500 = 0.164J
Actual energy, E2 = \(\frac{1}{2}\) mv2 = \(\frac{1}{2}\) × 3.35 × 10-5 × (10)2 = 1.675 × 10-3 J.
∴ Workdone by the resistive forces,
W = E1 – E2 = 0.164 – 1.675 × 10-3
W = 0.1623 Joule.
Question 14.
A molecule in a gas container hits a horizontal wall with speed 200 m s-1 and angle 30° with the normal and rebounds with the same speed. Is momentum conserved in the collision ? Is the collision elastic or inelastic ?
Answer:
We know that momentum is conserved in all collisions, elastic as well as inelastic. Let us now check if K. E is conserved (or) not.
If the wall is too heavy, the recoiling molecule produces no velocity in the wall.
If m is mass of the gas molecule and M is mass of wall, then total K.E after collision
E2 = – m(200)2 + \(\frac{1}{2}\) M(0)2
E2 = 2 × 104 mJ
Which is the K.E. of the molecule before collision.
[E1 = \(\frac{1}{2}\)m(200)2 = 2 × 104 mJ]
Hence the collision is elastic.
![]()
Question 15.
A pump on the ground floor of a building can pump up water to fill a tank of volume 30 m3 in 15 min. If the tank is 40 m above the ground and the efficiency of the pump is 30%, how much electric power is consumed by the pump ?
Answer:
Here, volume of water = 30 m2, t = 15 min = 15 × 60 = 900s.
height h = 40m, efficiency η = 30%
As density of water = ρ = 103 kg /m3
∴ Mass of water pumped, m = volume x density = 30 × 103 kg
Actual power consumed (or) out power
P0 = \(\frac{\mathrm{w}}{\mathrm{t}}=\frac{\mathrm{mgh}}{\mathrm{t}}\)
= \(\frac{30 \times 10^3 \times 9.8 \times 40}{900}\) = 10370 watt.
If Pi is input power (required), then as η = \(\frac{P_0}{P_i}\)
∴ Pi =\(\frac{P_0}{\eta}=\frac{10370}{\frac{30}{100}}\) = 43567 watt = 43.567 KW.
Question 16.
Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed V. If the collision ¡s elastic, which of the following (Fig.) is a possible result after collision ?
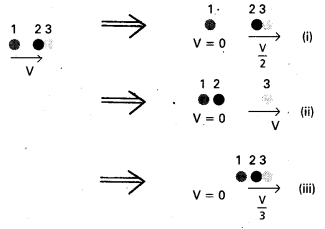
Answer:
Let m be the mass of each ball bearing
Before collision, total K.E of the system =
\(\frac{1}{2}\)mV2 + 0 = \(\frac{1}{2}\) mV2
After collision K.E of the system is
Case I, E1 = \(\frac{1}{2}\) (2m) (V/2)2 = \(\frac{1}{4}\) mV2
Case II, E2 = \(\frac{1}{2}\) mV2
Case III, E3 = – (3m) (V/3)2 = \(\frac{1}{6}\)mV2
We observe that is conserved only in Case II. Hence the Case II is the only possibility.
Question 17.
The bob A of a pendulum released from 30° to the vertical hits another bob B of the same mass at rest on a tables as shown in Fig. How high does the bob A rise after the collision ? Neglect the size of the bobs and assume the collision to be elastic.
Answer:
The bob A shall not rise. This is because when two bodies of same mass undergo an elastic collision, their velocities are interchanged. After collision, ball a will come to rest and the ball B would move with the velocity of A.
![]()
Question 18.
The bob of a pendulum is released from a horizontal position, If the length of the pendulum is 1.5 m, what is the speed with which the bob arrives at the lowermost point, given that it dissipated 5% of its initial energy against air resistance ?
Answer:
Here, h = 1.5m, V = ?
Energy dissipated = 5%
Taking B as the lowest position of the bob, its potential energy at B is zero. At the horizontal position, A total potential energy of the bob is mgh.
In going from A to B, P.E of the bob is converted into K.E
Energy conserved = 95% (mgh)
If V is velocity acquired at B, then K.E = \(\frac{1}{2}\) mv2
= \(\frac{95}{100}\)mgh
V = \(\sqrt{\frac{95}{100} \times 2 \mathrm{gh}}=\sqrt{\frac{19}{20} \times 2 \times 9.8 \times 1.5}\)
= 5.285ms-1.
Question 19.
A trolley of mass 300 kg carrying a sandbag of 25 kg is moving uniformly with a speed of 27 km/ h oh a frictionless track. After a while, sand starts leaking out of a hole on the floor of the trolley at the rate of 0.05 kg s-1. What is the speed of the trolley after the entire sand bag is empty ?
Answer:
As the trolley carrying the sane bag is moving uniformly, therefore, external force on the system = zero.
When the sand leaks out, it does not lead to the application of any external force on the trolley. Hence the speed of the trolley shall not change.
Question 20.
A body of mass 0.5 kg travels in a straight line with velocity v = ax3/2 where a = 5m-1/2 s-1. What is the workdone by the net force during its displacement from x = 0 to x = 2 m ?
Answer:
Here, m = 0.5 kg; v = ax3/2, a = 5m-1/2 s-1,
w = ?
Intial vel. at x = 0, v1 = a × 0 =0
Final vel, at x = 2, v2 = a23/2 = 5 × 23/2
Workdone = increase in K.E. = \(\frac{1}{2}\) m
(v22 – v12), W = \(\frac{1}{2}\) × 0.5 [(5 × 23/2)2) – 0]
= 50 J
![]()
Question 21.
The blades of a windmill sweep out a circle of area A.
(a) If the wind flows at a velocity v perpendicular to the circle, what is the mass of the air passing through it in time t ?
(b) What is the kinetic energy of the air ?
(c) Assume that the windmill converts 25% of the wind’s energy into electrical energy and that A = 30 m2, v = 36 km/h and the density of air is 1.2 kg m-3. What is the electrical power produced ?
Answer:
a) Volume of wind flowing /sec = AV
Mass of wind flowing / sec = AVρ
Mass of air passing in t sec = AVρt
b) K.E of air = \(\frac{1}{2}\) mv2 = \(\frac{1}{2}\) (AVρt)
v2 = \(\frac{1}{2}\) av3ρt.
c) Electrical energy produced = \(\frac{25}{100}\)
K.E of air = \(\frac{1}{4}\) × \(\frac{1}{2}\) × Av3ρt
Electrical power = \(\frac{1}{8} \frac{A v^3 \rho t}{t}=\frac{1}{8} A v^3 \rho t\)
P = \(\frac{1}{8}\) × 30 × (10)3 × 1.2 = 4500 watt
= 4.5 Kw.
Question 22.
A person trying to lose weight (dieter) lifts a 10kg mass, one thousand times, to a height of 0.5 m ech time. Assume that the potential energy lost each time she lowers the mass is dissipated,
(a) How much work does she do against the gravitational force ?
(b) Fat supplies 3.8 × 107J of energy per kilo-gram which is converted to mechanical energy with a 20% efficiency rate. How much fat will the dieter use up ?
Answer:
Here, m = 10 kg, h = 0.5 m, n = 1000
a) Workdone against gravitational force W = n(mgh)
= 1000 × (10 × 9.8 × 0.5 = 49000 J
b) Mechanical energy supplied by 1 kg of fat
= 3.8 × 10 × \(\frac{20}{100}\) = 0.76 × 107 J/kg
∴ Fat used up by the dieter
= \(\frac{1 \mathrm{~kg}}{0.76 \times 10^7}\) = 4000 = 6.45 × 10-3 kg.
Question 23.
A family uses 8 kW of power,
(a) Direct solar energy is incident on the horizontal surface at an average rate of 200 W per square meter. If 20% of this energy can be converted to useful electrical energy, how large an area is needed to supply 8 kW ?
(b) Compare this area to that of the roof of a typical house.
Answer:
Let area be A’ square meter
∴ Total power = 200A
Useful electrical energy produced/sec = \(\frac{20}{100}\)
(200A) = 8KW = 40A = 8000 (watt)
Therefore, A = \(\frac{8000}{40}\) = 200 sq.m
This area is comparable to the roof of a large house of 250 sq.mt.
![]()
Question 24.
A bullet of mass 0.012 kg and horizontal speed 70 ms-1 strikes a block of wood of mass 0.4 kg and instantly comes to rest with respect to the block. The block is suspended from the ceiling by means of thin wires. Calculate the height to which the block rises. Also, estimate the amount of heat produced in the block.
Answer:
Here m1 = 0.012kg. u1 = 70 m/s m2 = 0.4 kg, u2 = 0
As the bullet comes to rest w.r. to the block, the two behave as one body. Let v be the velocity acquired by the combination. Applying principle of conservation of linear momentum, (m1 + m2)v
= m1u1 + m2u2 = m1u1
V = \(\frac{m_1 u_1}{m_1+m_2}=\frac{0.012 \times 70}{0.012+0.4}=\frac{0.84}{0.412}\)
= 2.04 m/s.
Let the block rise to a height h.
RE of combination = K.E. of the combination
(m1 + m2)gh = \(\frac{1}{2}\) (m1 + m2)v2
h = \(\frac{v^2}{2 g}=\frac{2.04 \times 2.04}{2 \times 9.8}\) = 0.212m.
For calculating heat produced. We calculate energy lost (W). where
W = intial K.E of bullet – final K.E of combination
= \(\frac{1}{2}\) m1u12 \(\frac{1}{2}\) (m1 + m2)v2
= \(\frac{1}{2}\) × 0.012 (70)2 – \(\frac{1}{2}\) (0.412) (2.04)2
W = 29.4 – 0.86 = 28.54 Joule.
∴ heat produd. H = \(\frac{W}{j}=\frac{28.54}{4.2}\) = 6.8 cal.
Question 25.
A 1kg block situated on a rough incline is connected to a spring of spring constant 100 N m-1 as shown in Fig. The block is released from rest with the spring in the unstretched position. The block moves 10 cm down the incline before coming to rest. Find the coefficient of friction between the block and the incline. Assume that the spring has a negligible mass and the pulley is frictionless.
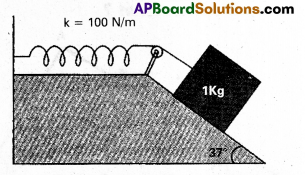
Answer:
From Fig.
R = mg cosθ
F = μR = μmg cosθ
Net force on the block down the incline
= mg sin θ – F = mg sin θ – μ mg cos θ
= mg (sin – μ cos θ)
Distanced moved, x = 10cm = 0.1m.
In equilibrium, work done = P.E of streched spring
mg (sin θ – μ cos θ) x = \(\frac{1}{2}\) Kx2
2mg (sin θ – μ cos θ) = Kx
2 × 1 × 10 (sin 37° – μ cos 37°) = 100 × 0.1
20(0.601 – μ 0.798) = 10
∴ μ = 0.126
![]()
Question 26.
A bob of mass 0.3 kg falls from the ceiling of an elevator moving down with an uniform speed of 7 ms-1. It hits the floor of the elevator (length of the elevator = 3 m) and does not rebound. What is the heat produced by the impact ? Would your answer be different if the elevator were stationary ?
Answer:
Here, m 0.3kg, v = 7 m/s h = length of elevator = 3m
As relative of the bob w.r.t elevator is zero, therefore, in the impact, only potential energy of the fall is converted into heat energy.
Amount of heat produced = P.E lost by the bob = mgh = 0.3 × 9.8 × 3 = 8.82 J.
The answer shall not be different, if the elevator were stationary as the bob too in that cause would start from stationary position, i.e. relative velocity of the ball w.r.t elevator would continue to be zero.
Question 27.
A trolley of mass 200 kg moves with a uniform speed of 36 km / h on a frictionless track. A child of mass 20 kg runs on the trolley from one end to the other (10 m away) with a speed of p m s-1 relative to the trolley in a direction opposite to the its motion and jumps out of the trolley. What is the final speed of the trolley ? Flow much has been trolley moved from the time the child begins to run ?
Answer:
Here, mass of trolley, m1 = 200 kg
speed of the trolley v = 36 km/h = 10m/s
mass of the child, m2 = 20 kg
Before the child starts running, momentum of the system.
P1 = (m1 + m2)v = (200 + 20)10
= 2200kg ms-1.
∴ Momentum of the system when the child is running
P2 = 200v1 + 20 (v1 – 4) = 220v1 – 80
As no external force is applied on the system.
∴ P2 = P1
220v1 – 80 = 2200
220v1 = 2200 + 80 = 2280
v1 = \(\frac{2280}{220}\) = 10.36 ms-1
Time taken by the child to run a distance of 10m over the trolley, t = \(\frac{10 \mathrm{~m}}{4 \mathrm{~ms}^{-1}}\) = 2.5 s
Distance moved by the trolley in this time = Velocity of trolley × time = 10.36 × 2.5 = 25.9 m
Question 28.
Which of the following potential energy curves in Fig. cannot possibly describe the elastic collision of two billiard balls ? Here r is the distance between centres of the balls.
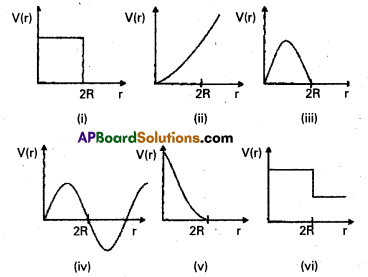
Answer:
The potential energy of a system of two masses varies inversely as the distance (r) between them i.e,
v(r) ∝ \(\frac{\mathrm{1}}{\mathrm{r}}\).
When the two billiard balls touch each other, P.E become zero i.e. at r = R + R = 2R;
v(r) = 0. Out of the given graphs, curve (v) only satisfies these two conditions.
![]()
Question 29.
Consider the decay of a free neutron at rest : n → p + e– Show that the two-body decay of this type must necessarily give an electron of fixed energy and, therefore, cannot account for the observed continuous energy distribution in the β-decay of a neutron or a nucleus (Fig.).
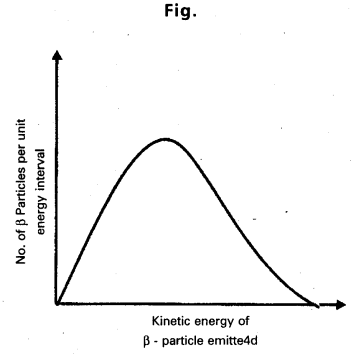
(Note : The simple result of this exercise was one among the several arguments advanced by W. Pauli to predict the existence of a third particle in the decay products of β-decay. This particle is known as neutrino. We now know that it is a particle of intrinsic spin 1/2 (like e-, p or n), but is neutral, and either masslessor having an extremely small mass (compared to the mass of electron) and which interacts very weakly with matter. The correct decay process of neutron is: n → p + e- + v
Answer:
In the decay process, n → p + e
energy of electrons is equal to (∆m)c2
Where ∆m = mass defect = mass of neutron – mass of proton and electron;
which is fixed. Therefore, two body decay of this type cannot explain the observed continuous energy distribution in the β-decay of a neutron or a nucleus.
Textual Examples
Question 1.
Find the angle between force F = \((3 \bar{i}+4 \bar{J}-5 \bar{k})\) unit and displacement d = \((3 \bar{i}+4 \bar{J}-5 \bar{k})\) unit. Also find the projection of F on d.
Answer:
F.d = Fxdx + Fydy + Fzdz = 3(5) + 4(4) + (-5)
(3) = 16 unit
Hence F.d = F d cos θ = 16 unit
Now F.F = F2 – Fx2 + Fy2 + Fz2
= 9 + 16 + 25 = 50 unit
and d.d = d2 = dx2 + dy2 + dz2
= 25 + 16 + 9 = 50 unit
∴ cosθ = \(\frac{16}{\sqrt{50} \sqrt{50}}=\frac{16}{50}\) = 0.32
= θ = cos-1 0.32.
Question 2.
It is well known that a raindrop falls under the influence of the downward gravitational force and the opposing resistive force. The latter is known to be proportional to the speed of the drop but is otherwise undetermined. Consider a drop of mass 1.00 g falling from a height 1.00 km. It hits the ground with a speed of 50.0 ms-1. (a) What is the work done by the gravitational force? What is the work done by the unknown resistive force?
Answer:
(a) The change in kinetic energy of the drop is
∆k = \(\frac{1}{2}\)mv2 – 0
= \(\frac{1}{2}\) × 10-3 × 50 × 50 = 1.25 J
where we have assumed that the drop is initially at rest.
Assuming that g is a constant with a value 10 m/s2, the work done by the gravitational force is,
Wg = mgh = 10-3 × 10 × 10-3 = 10.0 J
(b) From the work-energy theorem
∆K = Wg + Wr
Where Wr is the work done by the resistive force on the raindrop. Thus
Wr = ∆K – Wg = 1.25 – 10 = -8.75 J in negative.
![]()
Question 3.
A cyclist comes to a skidding stop in 10 m. During this process, the force on the cycle due to the road is 200 N and is directly opposed to the motion,
(a) How much work does the road do on the cycle ?
(b) How much work does the cycle do on the road ?
Answer:
Work done on the cycle by the road is the work done by the stopping (frictional) force on the cycle due to the road.
(a) The stopping force and the displacement make an angle of 180° (π rad) with each other.
Thus, work done by the road,
Wr = Fd cosθ = 200 × 10 × cos π
= -2000 J
It is this negative work that brings the cycle to a halt in accordance with WE theorem.
(b) From Newton’s Third Law an equal and opposite force acts on the road due to the cycle. Its magnitude is 200 N. However, the road, undergoes no displacement. Thus work done by cycle on the road is zero.
Question 4.
In a ballistics demonstration a police officer fires a bullet of mass 50.0g with speed 200 ms-1 (Bullet of mass = 5 × 10-2, Bullet of speed = 200; Bullet of K(J) = 103; on soft plywood of thickness 2.00 cm. The bullet emerges with only 10% of its initial kinetic energy. What is the emergent speed of the bullet ?
Answer:
The initial kinetic energy of the bullet is mv2 / 2 = 1000 J. It has a final kinetic energy of 0.1 × 1000 = 100 J. If vf is the emergent speed of the bullet,
\(\frac{1}{2}\) mv2f = 100 J
vf = \(\frac{\sqrt{2 \times 100 \mathrm{~J}}}{0.05 \mathrm{~kg}}\) = 63.2 ms-1
The speed is reduced by approximately 68% (not 90%).
![]()
Question 5.
A woman pushes a trunk on a railway platform which has a rough surface. She applies a force of 100 N over a distance of 10 m. Thereafter, she gets progressively tired and her applied force reduces linearly with distance to 50 N. The total distance through which the trunk has been moved is 20 m. Plot the force applied by the woman and the frictional force, which is 50 N versus displacement. Calculate the work done by the two forces over 20m.
Answer:
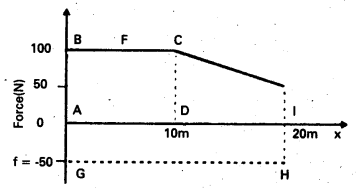
Plot of the force F applied by the woman and the opposing frictional force f versus displacement.
The plot of the applied force is shown in Fig. At x = 20 m, F = 50 N (≠ 0). We are given that the frictional force f is |f| = 50N. It opposes motion and acts in a direction opposite to F. It is therefore, shown on the negative side of the force axis.
The work done by the woman is
WF → area of the rectangle ABCD + area of the trapezium CEID
WF = 1000 × 10 + \(\frac{1}{2}\)(100 + 50) ×10
= 1000 + 750 = 1750 J
The work done by the frictional force is
Wf → area of the rectangle AGHI
Wf → (-50) × 20 = -1000 J
The area on the negative side of the x- axis has a negative sign.
Question 6.
A bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity v0 at the lowest point A such that it completes a semi circular trajectory in the vertical plane with the string becoming slack only on reaching the topmost point, C. This is shown in Fig. Obtain an expression for (i) v0 (ii) the speeds at points B and C; (iii) the ratio of the kinetic energies (KB/K) at B and C. Comment on the nature of the trajectory of the bob after it reaches the point C.
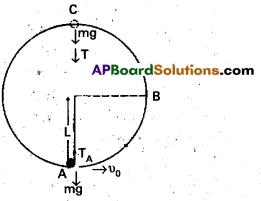
Answer:
Thus, at A:
E = \(\frac{1}{2} {\mathrm{mv}_0^2}\) ………………… (1)
TA – mg = \(\frac{\mathrm{mv}_0^2}{\mathrm{~L}}\) [Newtons Second Law]
where TA is the tension in the string at A. At the highest point C, the string slackens, as the tension in the string (Tc) becomes zero.
E = – \(\frac{1}{2} {\mathrm{mv}_c^2}\) + 2mgL ………………… (2) .
mg = \(\frac{\mathrm{mv}_c^2}{\mathrm{~L}}\) [Newtons Second law] ……………… (3)
where vc is the speed at C. From equations (2) & (3)
E = \(\frac{5}{2}\)mgL
Equating this to the energy at A
\(\frac{5}{2}\) mgL = \(\frac{m}{2} v_0^2\) or, v0 = \(\sqrt{5 \mathrm{gL}}\)
(ii) It is clear from Equation (3)
vc = \(\sqrt{ \mathrm{gL}}\)
At B, the energy is
E = \(\frac{1}{2} m v_B^2\) + mgL
Equating this to the energy at A and empLoying the result from (i),
namely v02 = 5gL
\(\frac{1}{2} m v_B^2+m g L=\frac{1}{2} m v_0^2\)
= \(\frac{5}{2}\)mgl ∴ vB = \(\sqrt{3\mathrm{gL}}\)
(iii) The ratio of the kinetic energies at Band C is :
\(\frac{\mathrm{K}_{\mathrm{B}}}{\mathrm{K}_{\mathrm{C}}}=\frac{\frac{1}{2} m v_{\mathrm{B}}^2}{\frac{1}{2} m v_{\mathrm{c}}^2}=\frac{3}{1}\)
At point C, the string becomes slack and the velocity of the bob is horizontal and to the left.
![]()
Question 7.
To simulate car accidents, auto manufactures study the collisions of moving cars with mounted springs of different spring constants. Consider a typical simulation with a car of mass 1000 kg moving with a speed 18.0 km / h on a smooth road and colliding with a horizontally mounted spring of spring constant 6.25 × 103 N m1. What is the maximum compression of the spring ?
Answer:
At maximum compression the kinetic energy of the car is converted entirely into the potential energy of the spring.
The kinetic energy of the moving car is 11
K = \(\frac{1}{2}\)mv2 = \(\frac{1}{2}\) × 103 × 5 × 5
K = 1.25 × 104 J
where we have converted 18 km h-1 to 5ms-1 [It is useful to remember that 36 km h-1 = 10 ms-1]. At maximum compression xm, the potential energy. V of the spring is equal to the kinetic energy K of the moving car from the principle of conservation of mechanical energy.
V = \(\frac{1}{2}\) K xm2 = 1.25 × 104 J
We obtain xm = 2.00 m
Question 8.
Consider example 8 taking the coefficient of friction, μ, to be 0.5 and calculate the maximum compression of the spring.
Answer:
In presence of friction, both the spring force and the frictional force act so as to oppose the compression of the spring as shown in Fig.
We invoke the work-energy theorem, rather than the conservation of mechanical energy.
The change in kinetic energy is
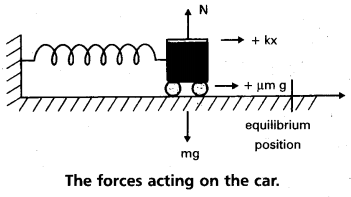
∆K = Kf – Ki = 0 – \(\frac{1}{2}\)mv2
The work done by the net force is
W = \(\frac{1}{2}\)Kxm2 – μm g xm
Equating we have
\(\frac{1}{2}\)mv2 = \(\frac{1}{2}\)K xm2 + μm g xm
Now μmg = 0.5 × 103 × 10 = 5 × 103 N
(taking g = 10.0 ms-2]. After rearranging the above equation we obtain the following quadratic equation in the unknown xm.
K xm2 + 2μm gxm – mv2 = 0
xm = \(\frac{-\mu m g+\left[\mu^2 m^2 g^2+m k v^2\right]^{1 / 2}}{k}\)
where we take the positive square root since xm is positive. Putting in numerical values we obtain
xm = 1.35 m
which, as expected, is less than the result in example 7
If the two forces on the body consist of a conservative force Fc and a non- conservative force Fnc, the conservation of mechanical energy formula will have to be modified. By the WE theorem
But Hence, (Fc + Fnc) ∆x = ∆K
Fc ∆x = ∆V
∆ (K + V) = Fnc ∆x
∆E = Fnc ∆x
where E is the total mechanical energy. Over the path this assumes the form Ef – Ei = Wnc
Where Wnc is the total work done by the non-conservative forces over the path. Note that unlike the conservative force. Wnc depends on the particular path i to f.
![]()
Question 9.
Examine express
(a) The energy required to break one bond in DNA in eV(1.6 × 10-19J);
(b) The kinetic energy of an air molecule (10-21J) in eV;
(c) The daily in take of a human adult in kilocalories (107).
Answer:
(a) Energy required to break one bond of DNA is \(\frac{10^{-20} \mathrm{~J}}{1.6 \times 10^{-19} \mathrm{~J} / \mathrm{eV}}\) ; 0.06 eV
Note 0.1 eV = 100 meV (100 millielectron volt).
(b) The kinetic energy of an air molecule is
\(\frac{10^{-21} \mathrm{~J}}{1.6 \times 10^{-19} \mathrm{~J} / \mathrm{eV}}\); 0.0062 eV
This is the same as 6.2 meV.
(c) The average human consumption in a day
is \(\frac{10^7 \mathrm{~J}}{4.2 \times 10^3 \mathrm{~J} / \mathrm{kcal}}\); 2400 kcaL
Question 10.
An elevator can carry a maximum load of 1800 kg (elavator + passengers) is moving up with a constant speed of 2ms-1. The frictional force opposing the motion is 4000 N. Determine the minimum power delivered by the motor to the elevator in watts as well as in horse power.
Answer:
The downward force on the elevator is F = mg + Ff = (1800 × 10) + 4000 = 22000 N
The motor must supply enough power to balance this force. Hence,
P = F.v = 22000 × 2 = 44000 W = 59 hp
Question 11.
Slowing down of neutrons : In a nuclear reactor of high speed (typically 107ms-1) must be slowed to 103 ms-1 so that it can have a high probability of interacting with isotope \({ }_{92}^{235} \mathrm{U}\) and causing it to fission. Show that a neutron can lose most of its kinetic energy in an elastic collision with a light nuclei like deuterium or carbon which has a mass of only a few times the neutron mass. The material making up the light nuclei, usually heavy water (D2O) or graphite, is called a moderator.
Answer:
The initial kinetic energy of the neutron is
K1i = \(\frac{1}{2}\) m1 v1i2
While its final kinetic energy from
V1f = \(\frac{\left(m_1-m_2\right)}{m_1+m_2}\) v1i2
K1f = \(\frac{1}{2}\)m1 v12f = \(\frac{1}{2}\)m1 \(\left(\frac{m_1-m_2}{m_1+m_2}\right)^2\) v1i2
The fractional kinetic energy lost is
f1 = \(\frac{K_{1 f}}{k_{1i}}\left(\frac{m_1-m_2}{m_1+m_2}\right)^2\)
while the fractional kinetic energy gained by the moderating nuclei K2f/ K1i is f2 = 1 – f1
elastic collision = \(\frac{4 m_1 m_2}{\left(m_1+m_2\right)^2}\)
One canalso verify this result by substituting from
v2f = \(\frac{2 m_1 v_1i}{m_1+m_2}\)
For deuterium m2 = 2m1 and we obtain f1 = 1/9 while f2 = 8/9. Almost 90% of the neutron’s energy is transferred to deuterium. For carbon f1 = 71.6% and f2 = 28.4%. In practice, however, this number is smaller since head-on collisions are rare.
![]()
Question 12.
Consider the collision depicted in Fig. to be between two billiard balls with equal masses m1 = m2. The first bail is called the cue while the second bail is called the target. The billiard player wants to ‘sink’ the target ball in a corner pocket, which is at an angle θ2 = 37°. Assume that the collision is elastic and that friction and rotational motion are not important. Obtain θ1.
Answer:
From momentum conservation, since the masses are equal
v1i = v1f + v2f
(or) v1i2 = (v1f + v2f). (v1f + v2f)
= v1f2 + V2f2 + 2v1fv2fcos (θ1 + 37°) …………….. (1)
Since the collision is elastic and m1 = m2 it follows from conservation of kinetic energy that
v1i2= v1f2 + v2f2 ………………. (2)
Comparing equations (1) and (2), we get
cos (θ1 + 37°) = 0
or θ1 +37° = 90°
Thus, θ1 = 53°
This proves the following results : When two equal masses undergo a glancing elastic collision with one of them at rest, after the collision, they will move at right angles to each other.