AP Inter 1st Year Physics Study Material Chapter 7 Systems of Particles and Rotational Motion

Andhra Pradesh BIEAP AP Inter 1st Year Physics Study Material 7th Lesson Systems of Particles and Rotational Motion Textbook Questions and Answers.

AP Inter 1st Year Physics Study Material 7th Lesson Systems of Particles and Rotational Motion

Very Short Answer Questions

Question 1.
Is it necessary that a mass should be present at the centre of mass of any system?
Answer:
No. Any mass need not be present at the centre of mass of a system.
Ex : a hollow sphere, centre of mass lies at its centre.

Question 2.
What is the difference in the positions of a girl carrying a bag in one of her hands and another girt carrying a bag in each of her two hands?
Answer:
When the girl carries a bag in one hand (left) her centre of mass shifts towards the other hands (right). In order to bring it in the middle, the girl has to lean towards her other side. When the girl carries a bag in each of her two hands (left and right), the centre of mass does not shift. The girl does not bend any side because of the same hags’ .w in her two hands.

Question 3.
Two rigid bodies have same moment of inertia about their axes of symmetry. Or the two, which body will have greater kinetic energy?
Answer:
E = \(\frac{1}{2}\) I ω² = \(\frac{1}{2} \frac{\mathrm{L}^2}{1}\) , E oc \(\frac{1}{l}\) (∵ L = constant)
The rigid body having less moment of inertia will have greater kinetic energy.

Question 4.
Why are spokes provided in a bicycle wheel ?
Answer:
By connecting to the rim of wheel to the axle through the spokes the mass of the wheel gets concentrated at its rim. This increases its moment of inertia. This ensures its uniform speed.

Question 5.
We cannot open or close the door by applying force at the hinges, why ?
Answer:
When the force is applied at the hinges, the line of action of the force passes through the axis of rotation i.e, r = 0, so we can not open or close the door by pushing or pulling it at the hinges.

Question 6.
Why do we prefer a spanner of longer arm as compared to the spanner of shorter arm ?
Answer:
The torque applied on the nut by the spanner is equal to the force multiplied by the perpendicular distance from the axis of rotaion.
A spanner with longer arm provides more torque compared to a spanner with shorter arm. Hence longer arm spanner is preferred.

Question 7.
By spinning eggs on a table top, how will you distinguish a hard boiled egg from a raw egg ? [Mar. 13]
Answer:
A raw egg has some fluid in it and a hard boiled egg is solid form inside. Both eggs are spinning on a table top, the fluid is thrown outwards. Therefore (I_r > I_b) That means M. I of raw egg is greater than boiled egg. As I × ω = constant; ∴ ω_r < ω_b. That means Angular Velocity of raw egg is less than angular velocity of boiled egg.

Question 8.
Why should a helicopter necessarily have two propellers ?
Answer:
If there were only one propeller in the hellicopter then, due tio conservation of angular momentum, the helicopter itself would have turned in the opposite direction. Hence, if should have two propellers.

Question 9.
It the polar ice caps of the earth were to melt, what would the effect of the length of the day be ?
Answer:
Earth rotates about its polar axis. When ice of polar caps of earth melts, mass concentrated near the axis or rotation spreads out. Therefore, moment of Inertia I increases.

As no external torgue acts, L = I × ω = \(I\left(\frac{2 \pi}{T}\right)\)= constant. With increase of I, T will increase i.e. length of the day will increase.

Question 10.
Why is it easier to balance a bicycle in motion?
Answer:
When a bicycle is in motion, it is easy to balance because the principle of conservation of angular momentum is involved.

Short Answer Questions

Question 1.
Distinguish between centre of mass and centre of gravity. [A.P. – Mar. ‘18, ‘16, ‘15, ‘14, ‘13; TS – Mar. ‘16, ‘15, ‘14, ‘13]
Answer:
Centre of mass

1. Point at which entire mass of the body is supposed to be concentrated, and the motion of the point represents motion of the body.
2. It refers mass of to body.
3. In a uniform gravitational field centre of mass and centre of gravity coincide
4. Centre of mass of the body is defined to describe the nature of motion of a body as a whole.

Centre of gravity

1. Fixed point through which the weight of the body act.
2. It refers to the weight acting on all particles of the body
3. In a non-uniform gravitational field, centre of gravity and centre of mass do not coincide.
4. Centre of gravity of body is defined to know the amount of stability of the body when supported.

Question 2.
Show that a system of particles moving under the influence of an external force, moves as if the force is applied at its centre of mass.
Answer:
Consider \(\overrightarrow{r_1}, \overrightarrow{r_2}, \overrightarrow{r_3} \ldots \ldots \overrightarrow{r_n}\) be the position vectors of masses m₁, m₂, m₃ …………. m_n of n particle system.
According to Defination of centre of mass.

Differentiating the above equation w.r.t. time, we obtain

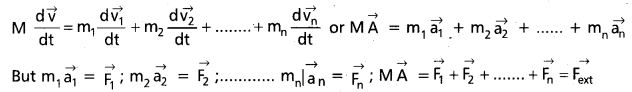
Where F_ext represents the sum of all external forces acting on the particles of the system. This equation states that the centre of mass of a system of particles moves as if all the mass of the system was concentrated at the centre of mass and all the external forces were applied at that point.

Question 3.
Explain about the centre of mass of earth-moon system and its rotation around the sun.
Answer:
In the solar system the planets have different velocities and have complex two dimensional motion. But the motion of the centre of mass of the planet is simple and translational. consider the earth and moon system. We consider that the earth is moving around the sun in an elliptical path. But actually the centre of mass of earth and moon moves in an elliptical path round the sun. But the motion of either earth or moon is complicated when considered separately, more over we say that moon goes round the earth.

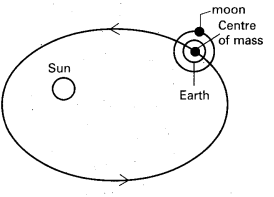
But actually earth and moon are revolving round their centre of mass such that they are always on opposite sides of the centre of mass. Here the forces of attraction between earth and moon are internal forces.

Question 4.
Define vector product. Explain the properties of a vector product with two examples. [T.S. AP – Mar. 15]
Answer:
The cross product of two vectors is given by \(\vec{C}=\vec{A} \times \vec{B}\). The magnitude of the vector defined from cross product of two vectors is equal to product of magnitudes of the vectors and sine of angle between the vectors.

Direction of the vectors is given by right hand corkscrew rule and is perpendicular to the plane containing the vectors.
∴ \(|\vec{C}|\) = AB sin θ. and \(\vec{C}\) = AB sin θ \(\hat{n}\). Where, \(\hat{n}\) is the unit vector perpendicular to the plane containing the vectors \(\vec{A}\) and \(\vec{B}\)
Example: 1) Torque is cross product of position vector and Force. i.e., \(\overrightarrow{\mathrm{T}}=\vec{r} \times \vec{F}\)
2) Angular momentum is cross product of position vector and momentum
i.e., \(\vec{L}=\vec{r} \times \vec{p}\)

Properties:

1. Cross product does not obey commutative law. But its magnitude obeys commutative low.
   \(\vec{A} \times \vec{B} \neq \vec{B} \times \vec{A} \Rightarrow(\vec{A} \times \vec{B})=-(\vec{B} \times \vec{A}),|\vec{A} \times \vec{B}|=|\vec{B} \times \vec{A}|\)
2. It obeys distributive law \(\vec{A} \times(\vec{B} \times \vec{C})=\vec{A} \times \vec{B}+\vec{A} \times \vec{C}\)
3. The magnitude of cross product of two vectors which are parallel is zero.
   Since θ = 0; \(|\vec{A} \times \vec{B}|\) = AB sin 0° = 0
4. For perpendicular vectors, θ = 90°, \(|\vec{A} \times \vec{B}|\) = AB sin 90° \(|\hat{n}|\)= AB

Question 5.
Define angular velocity(u). Derive v = r ω. [T.S. Mar. 16]
Answer:
Angular velocity (ω):
The rate of change of angular displacement of a body is called angular velocity, i.e., ω = \(\frac{\mathrm{d} \theta}{\mathrm{dt}}\)
Derivation of v = rω
consider a rigid body be moving with uniform speed (v)along the circumference of a circle of radius r. Let the body be displaced from A to B in a small interval of time At making an angle ∆θ at the cantre. Let the linear displacement be ∆x from A to B.
From the property of circle, length of arc = radius × angle
∆x = r ∆θ
This equation is divided by ∆t, and taking

Question 6.
Define angular acceleration and torque. Establish the relation between angular acceleration and torque. [T.S. Mar. 18]
Answer:
Angular acceleration :
The rate of change of angular velocity is called angular acceleration
i.e., α = \(\frac{\mathrm{d} \omega}{\mathrm{dt}}\)
Torque : The rate of change of angular momentum is called torque or The moment of Force is called Torque.

Relation between angular acceleration and Torque: Consider a rigid body of mass ‘M’ rotating in a circular path of radius ‘R’ with angular velocity ‘ωω’ about fixed axis.

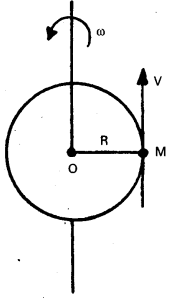
By definition, τ = \(\frac{\mathrm{dL}}{\mathrm{dt}}=\frac{\mathrm{d}(\mathrm{I} \omega)}{\mathrm{dt}}\)
Where I = MR² = moment of inertia of a body
τ = I \(\frac{\mathrm{d} \omega}{\mathrm{dt}}\) [∵ I = constant]
But \(\frac{\mathrm{d} \omega}{\mathrm{dt}}\) α
∴ τ = Iα

Question 7.
Write the equations of motion for a particle rotating about a fixed axis?
Answer:
Equations of motion for a particle rotating about a fixed axis:
1. ω_f = ω_f + αt [∵ like v = u + at]
2. θ = \(\left(\frac{\omega_f+\omega_t}{2}\right) t\) [∵ like v = \(\left(\frac{v_1+v_2}{2}\right) t\)]
3. θ = ω_it + \(\frac{1}{2}\) α t² [∵ like s = ut + \(\frac{1}{2}\) at²]
4. ω_f² – ω_i² = 2 α θ [∵ like v² – u² = 2as]
Where ω_i = Initial angular velocity
ω_f = Final angular velocity
α = Angular acceleration
θ = Angujar displacement
t = time

Question 8.
Derive expressions for the final velocity and total energy of a body rolling without slipping.
Answer:
Expression of velocity of a body Rolling down an inclined plane:
Consider a rigid body of mass M and radius R rolling down an inclined plane from a height h . Let v the linear speed acquired by the body when it reaches the bottom of the plane and k is its radius of gyration.

According to law of conservation of Energy, we have P.E of body on top of inclined plane = K.E of a body at the bottom of inclimed plane
When a body rolls down an incline of height h, we apply the principle of conservation of energy.
P.E at the top – K.E of translation + K.E of rotation

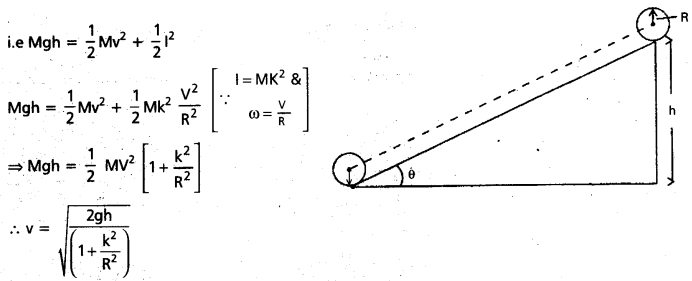
Expression of Total energy of a body Rolling down on an inclined plane:
Suppose a body (Sphere) is rolling on a surface. Its motion can be treated as a combination of the translation of the centre of mass and rotation about an axis passing through the centre of mass. The total kinetic energy E can written as
E = E_T + E_R
Where E_T = Translational kinetic energy
and E_R = Rotational kinetic energy
E = \(\frac{1}{2}\) Mv² + \(\frac{1}{2}\) Iω²
= \(\frac{1}{2}\) MR² ω² + \(\frac{1}{2}\) Mk²ω²
E = \(\frac{1}{2}\) M ω² (R² + K²)
where k is radius of gyration
E = \(\frac{1}{2}\) Mv² (1 + \(\frac{K^2}{R^2}\)) [∵ ω = \(\frac{V}{R}\)]

Long Answer Questions

Question 1.
a) State and prove parallel axis theorem.
Answer:
Statement: The moment of inertia of a rigid body about any axis is equals to the sum of moment of inertia about a parallel axis passing through centre of mass (lg) and product of mass of body and square of perpendicular distance between two parallel axis.
∴ I = I_G + mr²
Proof : Consider a rigid body of mass M. Let I and I_G are the moment of inertia of a body about parallel axes X and Y respectively.

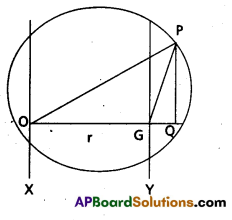
Let ‘r’ be the perpendicular distance between two axes.
Moment of inertia about ‘X’ axes is
I = Σm(OP)² ………………. (1)
Moment of inertia about Y axes is
I_G = Σm(GP)² …………….. (2)
from ∆⁴ OQP, OP² = (OQ)² + (PQ)²
= (OG + GQ)² + (PQ)²
= OG² + (GQ)² + 2.OG.GQ + (PQ)²
= OG² + (GP)² + 2(OG) (GQ) (∴ (GP)² = (GQ)² + (PQ)²)
Multiplying both sides by Σm,
⇒ Σm(OP)² = Σm(OG)² + Σm(GP)² + 2Σm(OG)(GQ)
from (1) and (2), I = mr² + IG + 2Σm (OG) (GQ)
But sum of moments of particles about centre of mass is zero.
i.e., Σm (OG) (GQ) = 0
∴ I = I_G + mr²
Hence proves.

b) For a thin flat circular disk, the radius of gyration about a diameter as axis is k. If the disk is cut along a diameter AB as shown in to two equal pieces, then find the radius of gyration of each piece about AB.

Answer:
For thin circular disk, the radius of gyration about a diameter
AB is, K = \(\sqrt{\frac{I}{M}}\)
Where M = mass of disk
I = M.I of disk
The disk is cut into two halves about AB, when each,
Mass M’ = \(\frac{\mathrm{M}}{\mathrm{2}}\) and each M.I, I = \(\frac{1}{2}\)
Therefore Radius of gyration of each piece is
K’ = \(\sqrt{\frac{I^{\prime}}{M^{\prime}}}=\sqrt{\frac{\left(\frac{I}{2}\right)}{\left(\frac{M}{2}\right)}}=\sqrt{\frac{I}{M}}\) = k

Question 2.
a) State and prove perpendicular axes theorem.
Answer:
Statement: The moment of inertia of a plane lamina about an axes perpendicular to its plane is equal to sum of moment of inertia of lamina about the perpendicular axes in its plane intersecting each other at a point, where the perpendicular axes passes.
i.e., I_z = I_x + I_y
Proof’ Consider a particle of mass’m’ at p. Let it be at a distance Y from Z-axis. Here ‘X’ and Y axes are in plane Ramina and Z-axes perpendicular to plane lamina.

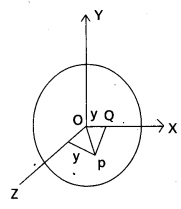
Now,
Moment of inertia about X-axix, I_x = Σmx²
Moment of inertia about Y-axis, I_y = Σmy²
Moment of inertia about Z-axis, I_z = Σmr²
From ∆⁴ OQP, r² = x² + y²
multiplying both side with Σm,
⇒ Σmr² = Σmx² + Σmy²
⇒ I_z = I_x + I_y
Hence proved.

b) If a thin circular ring and a thin flat circular disk of same mass have same moment of inertia about their respective diameters as axes. Then find the ratio of their radii.
Answer:
For a thin flat circular dist, M.I., I_r = \(\frac{\mathrm{MR}_{\mathrm{r}}^2}{2}\)
For a thin flat circular dist, M.I., I_d = \(\frac{\mathrm{MR}_{\mathrm{d}}^2}{2}\)
Given that I_r = I_d
\(\frac{M R_r^2}{2}=\frac{M R_d^2}{4} \Rightarrow \frac{R_r^2}{R_d^2}=\frac{2}{4}=\frac{1}{2}\)
∴ \(\frac{R_r}{R_d}=\frac{1}{\sqrt{2}} \text { or } R_r: R_d=1: \sqrt{2}\)

Question 3.
State and prove the principle of conservation of angular momentum. Explain the principle of conservation of angular momentum with examples. [A.P. Mar 16]
Answer:
Statement: Angular momentum of a body remains constant when the external torque is zero.
L = I ω = constant K.
or I₁ ω₁ = I₂ ω₂.
If the moment of Inertia of a body is lowered, the angular velocity of the body co increases.
Proof:
By derfination, the rate of change of angular momentum is called Torque.
i.e., τ = \(\frac{\mathrm{dL}}{\mathrm{dt}}\)
If τ = 0 ⇒ \(\frac{\mathrm{dL}}{\mathrm{dt}}\) = 0
or L = constant k
⇒ L₁ = L₂
∴ I₁ ω₁ = I₂ ω₂
Example 1): When a man with stretched out arms stands on a turn table which is revolving then his moment of inertia is high. If he folded his hands, the moment of inertia decreases and hence the angular velocity, linear velocity increase, but the period decreases. In both cases angular momentum remains constant.

Example 2): An acrobat from a swing in a circus, leaves the swing with certain angular momentum, with his arms and legs stretched. As soon as he leaves the swing he pulls his hands and legs together thus lowering his M.I. and increasing his angular velocity. He then quickly makes somersaults in air and finally lands on a net or ground.

Problems

Question 1.
Show that a(b × c) is equal in magnitude to the volume of the parallelepiped formed on the three vectors a, b and c.
Solution:
Let a parallele piped be formed on three vectors.

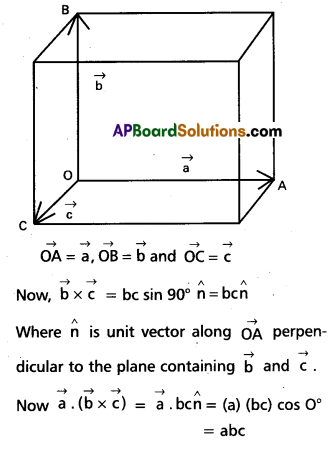
Which is equal in magnitude to the volume of the parallel piped.

Question 2.
A rope of negligible mass is wound 4. round a hollow cylinder of mass 3kg and redius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30N ? What is the linear acceleration of the rope ? Assume that there is no slipping.
Solution:
Here M = 3kg, R = 40 cm = 0.4 m
Moment of intertia of the hollow cylinder about its axis
I = MR² = 3(0.4)² = 0.48 kgm²
Force applied F = 30 N
∴ Torque, τ = F × R= 30 × 0.4 = 12 N – m.
If α is the angular acceleration, produced, then from τ = Iα
α = \(\frac{\tau}{\mathrm{l}}=\frac{12}{0.48}\) = 25 rads^-2
Linear acceleration, a = Rα = 0.4 × 25 = 10 m/s²

Question 3.
A coin is kept a distance of 10 cm from the centre of a circular turntable. If the coefficient of static friction between the table and the coin is 0.8 find the frequency of rotation of the disc at which the coin will just begin to slip.
Solution:
Here, radius, r = 10cm = 0.1 m; μ_s = 0.8
F = μmg
mrω² = μmg
rω² = μg
ω = \(\frac{\mu \mathrm{g}}{\mathrm{r}}=\sqrt{\frac{0.8 \times 9.8}{0.1}}=\sqrt{8 \times 9.8}\)
= 8.854 rad/s
w = 2πn
∴ frequency n = \(\frac{\omega}{2 \pi}=\frac{8.854}{2 \times 3.14}\) = 1 .409rps
n = 1.409 × 60 = 84.54 rpm

Question 4.
Particles of masses 1g, 2g, 3g…. 100g are kept at the marks 1 cm. 2cm, 3cm ….100cm respectively on 2 meter scale. Find the moment of inertia of the system of particles about a perpendicular bisector of the meter scale. –
Solution:
By adding all the masses, we get M = 5050g
= 5.050 kg
= 5.1 kg
and L = 1 m
M.I. of the meter scale = \(\frac{\mathrm{mL}^2}{12}=\frac{5.1 \times 1^2}{12}\)
= 0.425kg m²
= 0.43kg -m²

Question 5.
Three particles each of mass 100g are placed at the vertices of an equilateral triangle of side length 10 cm. Find the moment of inertia of the system about an axis passing through the centroid Of the triangle and perpendicular to its plane.
Solution:
m = 100 g = 100 × 10^-3kg
Side a = 10 cm

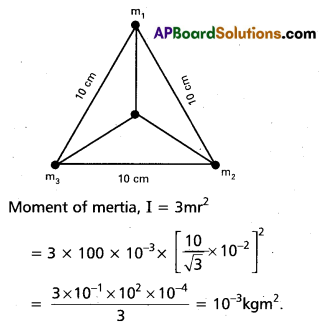
Question 6.
Four particles each of mass 100g are placed at the corners of a square of side 10 cm. Find the moment of inertia of the system about an axis passing through the centre of the square and perpendicular to its plane. Find also the radius of gyration of the system.
Solution:
mass m = 100g
= 100 × 10^-3kg
M = 4m = 400 × 10^-3kg
radius r = 10cm
= 10 × 10^-2m
Moment of Inertia I = Mr²

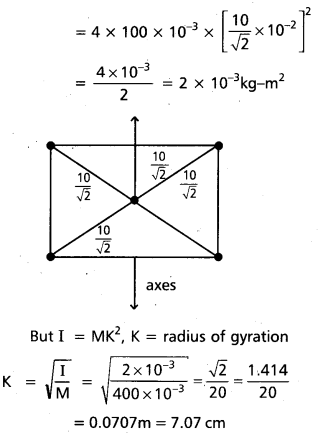
Question 7.
Two uniform circular discs, each of mass 1 kg and radius 20 cm, are kept in contact about the tangent passing through the point of contact. Find the moment of inertia of the system about the tangent passing through the point of contact.
Solution:
Mass m = 1kg; r = 20cm = 20 × 10^-2m
I = I₁ + I<sub2

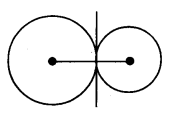
I₁ = \(\frac{\mathrm{MR}^2}{4}\) + MR²
I₁ = \(\frac{5\mathrm{MR}^2}{4}\)
Similarly I₂ = \(\frac{5\mathrm{MR}^2}{4}\)
∴ I = \(\frac{10 \mathrm{MR}^2}{4}=\frac{10 \times 1 \times\left(20 \times 10^{-2}\right)^2}{4}\) = 0.1 kg-m²

Question 8.
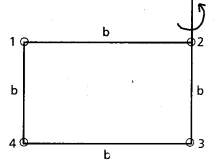
Four spheres, each diameter 2a and mass ‘m’ are placed with their centres on the four corners of a spuare of the side b. Calculate the moment of inertia of the system about any side of the square.
Solution:
I₁ = mb²
I₂ = \(\frac{2}{5}\) ma²
I₃ = \(\frac{2}{5}\) ma²
I₄ = mb²
∴ Moment of inertia of the system
I = I₁ + I₂ + I₃ + I₄
= mb² + \(\frac{2}{5}\) ma² + \(\frac{2}{5}\) ma² + mb²
I = \(\frac{4}{5}\) ma² + 2mb²

Question 9.
To maintain a rotor at a uniform angular speed or 200 rads^-1, an engine needs to transmit a torque of 180 Nm. What is the power required by the engine ? (Note : uniform angular velocity in the absence of friction implies zero torque. In practice applied torque is needed to counter frictional torque). Assume that the engine is 100% efficient.
Solution:
Here, ω = 200 rad/s, torque τ = 180 N – m, power p = ?
As p = τ ω
∴ p = 180 × 200 = 3600.watt = 36 kw.

Question 10.
A metre stick is balanced on a knife edge at its centre. When two coins, each of mass 5g are put one on top of the other at the 12.0 cm mark, the stick is found to be balanced at 45.0 cm. What is the mass of the metre stick ?
Solution:
Let M be the mass of stick concentrated at L, the 50 cm, mark.
For equilibrium about G’ the 45 cm mark,
10g (45 – 12) = mg(50 – 45)
10 g × 33 = mg × 5
M = \(\frac{10 \times 33}{5}\) = 66 gram.

Question 11.
Determine the kinetic energy of a circular disc rotating with a speed of 60 rpm about an axis passing through a point on its circumference and perpendicular to its plane. The circular disc has a mass of 5kg and radius 1m.
Solution:
Here M = 5kg; R = 1 m;
ω = 2π × \(\frac{\mathrm{N}}{\mathrm{t}}\) = 2n × \(\frac{60}{60}\) rad /s = 2π rad/s
The M.I of disc about parallel axis passing through a point on its circumferance
I = \(\frac{\mathrm{MR}^2}{2}\) + MR² = \(\frac{3}{2}\) MR²
∴ Kinetic energy = \(\frac{1}{2}\) I ω²
= \(\frac{1}{2}\) × \(\frac{3}{2}\) MR² ω² = \(\frac{3}{4}\) × 5 × (1)² × (2π)²
= \(\frac{3}{4}\) × 5 × 4π² = 15 × (\(\frac{22}{7}\)²
∴ K.E = 148.16 J.

Question 12.
Two particles each of mass m and speed v Travel in opposite directions along parallel lines separated by a distance. Show that the vector angular momentum of the two particle system is the same whatever be the point about which the angular momentum is taken.
Solution:
Given that m₁ = m₂ = m;
\(\vec{V}_1=\vec{V}_2=\vec{V}\)
momentum of 1^st particle p₁ = \(\mathrm{m} \vec{\mathrm{V}}\)
∴ p₁ = \(\mathrm{m} \vec{\mathrm{V}}\)
momentum of 2^nd particle \(\vec{\mathrm{P}}_2=\mathrm{mV}\)

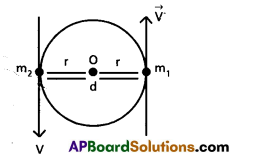
If two particles moves oppositely on
Circumference of circle, distance d = 2r
Angular momentum of 1^st particle w.r.t
Centre ‘O’ is \(\vec{L_1}=\vec{r} \times \vec{P}_1=\vec{r} \times m \vec{V}\)
Angular momentum of 2^nd particle w.r.t
centre ‘O’ is \(\vec{\mathrm{L}_2}=\vec{\mathrm{r}} \times \vec{\mathrm{P}_2}=\vec{\mathrm{r}} \times \mathrm{m} \vec{\mathrm{V}}\)
∴ \(\vec{L_1}=\vec{L_2}\)

Question 13.
The moment of inertia of a fly wheel making 300 revolutions per minute is 0.3 kgm ² Find the torque required to bring it to rest in 20s.
Solution:

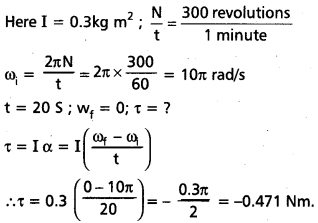
Question 14.
When 100 J of work is done on a fly wheel, its angular velocity is increased from 60 rpm to 180 rpm. What is the moment of inertia of the wheel ?
Solution:
Here, Initial frequency
n₁ = \(\frac{60}{60}\) = 1Hz
Initial angular velocity
ω₁ = 2π n₁ = 2π rad /sec
Final frequency n₂ = \(\frac{180}{60}\) = 3Hz
Final angular velocity
ω₂ = 2π n₂ = 2π × 3 = 6π rad/sec
Work done = 100 J from work – energy therorem,
Workdone = change in K.E.
W = \(\frac{1}{2}\) I ω₂² – \(\frac{1}{2}\) I ω₁²
100 = \(\frac{1}{2}\) I [(6π)² – (2π)²]
100 = \(\frac{1}{2}\) I (32π)²
I = \(\frac{200}{32 \pi^2}\) = 0.634 kg – m²
∴ I = 0.634 kg- m²

Additional Problems

Question 1.
Give the location of the centre of mass of a (i) sphere (ii) cylinder (iii) ring and (iv) cube. each of uniform mass density. Does the centre of mass of a body necessarily lie inside the body?
Solution:
In all the four cases, as the mass density is uniform, centre of mass is located at their respective geometrical centres.
No, it is not necessary that the center of mass of a body should lie on the body for example in caSe of a circular ring. Center of mass is at the centre of the ring, where there is no mass.

Question 2.
In the HCl molecule the separation between the nuclei of the two atoms Is about 1.27 Å(1 Å = 10^-10m). Find the approximate location of the CM of the molecule, given that a chlorine atom is about 35.5 times as massive as a hydrogen atom and nearly all the mass of an atom Is concentrated in its nucleus.
Solution:
Let the mass of the H atom = m unit, mass of the Cl atom = 35.5 m units
Let cm be at the distance xÅ from Htom
∴Distance of cm from CL atom = (1.27 – x) Å
It cm is taken at the origin,
then mx + (1.27 – x) 55.5m = 0
mx = (1.27 – x) 35.5 m.
Negative sign indicates that if chlorine atom is on the right side of cm (+), the hydrogen atom is on the left side of cm, so leavning negative sign, we get
x + 35.5 x = 1.27 × 35.5
36.5 x = 45.085
x = \(\frac{45.085}{36.5}\)
= 1.235
x = 1.235 Å
Hence cm is located on the line joining centres of H and d atoms at a distance 1.235 Å from H.

Question 3.
A child sits stationary at one end of a long trolley moving uniformly with a speed V on a smooth horizontal floor. If the child gets up and runs about on the trolley in any manner, what is the speed of the CM of the (trolley + child) system ?
Solution:
The speed of the centre of mass of the system , (trolley + child) shall remain unchanged, when the child gets up and runs about on the trolley in any manner. This is because forces involved in the exercise are purely internal i.e., from within the system. No external force acts on the system and hence there is no change in velocity of the system.

Question 4.
Show that the area of the triangle contained between the vectors a and b is one half of the magnitude of a × b
Solution:
Let \(\vec{\mathrm{a}}\) represented by \(\vec{\mathrm{OP}}\) and \(\vec{\mathrm{b}}\) be represented by \(\vec{\mathrm{OQ}}\).
Let ∠POQ = θ

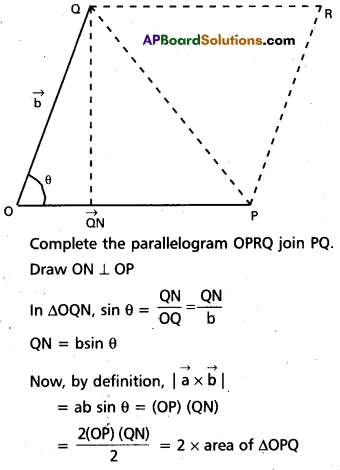
∴ area of ∆ OPQ = \(\frac{1}{2}|\vec{a} \times \vec{b}|\), which was to be proved.

Question 5.
Show that a.(b × c) is equal in magnitude to the volume of the parallelepiped formed on the three vectors a, b and c.
Solution:
Let a parallel piped be formed on three vectors.

Where \(\hat{n}\) is unit vector along \(\overrightarrow{\mathrm{OA}}\) perpendicular to the plane containing \(\) and \(\vec{\mathrm{b}}\). Now \(\vec{\mathrm{b}}\) = (a) (be) cos 0°
= abc
Which is equal in magnitude to the volume of the parallelepiped.

Question 6.
Find the components along the x. y. z axes of the angular momentum 1 of a particle whose position vector is r with components x, y, z and momentum is p with components p_x, p_y, and p_z,. Show that if the particle moves only in the x-y plane the angular momentum has only a z-component.
Solution:
For motion in 3D, the position vector \(\vec{\mathrm{r}}\) and linear momentum vector \(\vec{\mathrm{p}}\) can be written in terms of their rectangular components as follows.

Comparing the coefficient of k on both sides, we have L_z = xp_y – yp_x.
Therefore the particle moves only in x-y plane. The angular momentum has only z component.

Question 7.
Two particles, each of mass m and speed v. travel in opposite directions along parallel lines separated by a distance d. Show that the vector angular momentum of the two particle system is the same what ever be the point about which the angular momentum is taken.
Solution:
From fig, vector angular momentum of the two particle system any point A on x₁ y₁ is.

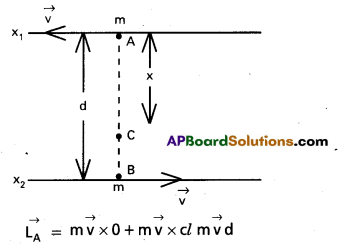
Similary, vector angular momentum of the tw.o particle system, a bout any pt. B on x₂y₂ is
\(\vec{L_B}=m \vec{v} \times d+m \vec{v} \times 0=m \vec{v} d\)
Let us consider any other point (on AB, where AC = x)
∴ Vector angular momentum of the two particle system about c is
\(\vec{L_c}=m \vec{v}(x)+m \vec{v}(d-x)=m \vec{v} d\)
Clearly, \(\vec{\mathrm{L}_{\mathrm{A}}}=\vec{\mathrm{L}_{\mathrm{B}}}=\vec{\mathrm{L}_C}\)
Which has to be proved.

Question 8.
A non-uniform bar of weight W is suspended at rest by two strings of negligible weight as shown in figure. The angles made by the strings with the vertical are 36.9 and 53.1° respectively. The bar is 2 m long. Calculate the distance d of the centre of gravity of the bar from its left end.
Solution:

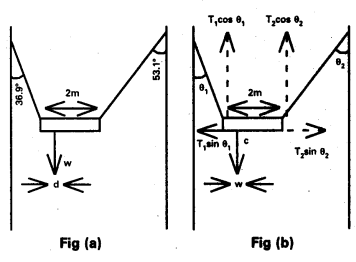
From fig (b)
θ₁ = 36.9°, θ₂ = 53.1°
If T₁, T₂ are the tensions in two strings, then for equilibrium along the horizontal,
T₁ sin θ₁ = T₂ sin θ₂
(or) \(\frac{T_1}{T_2}=\frac{\sin \theta_2}{\sin \theta_1}=\frac{\sin 53.1^{\circ}}{\sin 36.9^{\circ}}\)
= \(\frac{0.7407}{0.5477}\) = 1.3523
Let d be the distance of center of gravity c of the bar from the left end.
For rotational equilibrium about c,
T₁ cos θ₁ Xd = T₂ cos θ₂ (2 – d)
T₁ cos 36.9° × d = T₂ cos 53.1° (2 – d)
T₁ × 0.8366 d = T₂ × 0.6718 (2 – d)
Put T₁ = 1.3523 T₂ and solve to get
d = 0.745 m.

Question 9.
A car weight 1800 kg. The distance between its front and back axles is 1.8 m. Its centre of gravity is 1.05 m behind the front axle. Determine the force exerted by the level ground on each front wheel and each back wheel.
Solution:
Here, m = 1800 kg
Distance between front and .back axles = 1.8 m
Distance of center of gravity (c) behind the front axle = 1.05 m
Let R₁ and R₂ be the forces exerted by the level ground on each front wheel and each back wheel. As it is dear from fig.
R₁ + R₂ = mg = 1800 × 9.8

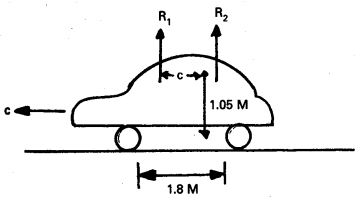
For rotational equilibrium about C,
R₁ × 1.05 = R₂ (1.8 – 1.05) = R₂ × 0.75 ………….. (i)
\(\frac{R_1}{R_2}=\frac{0.75}{1.05}=\frac{5}{7}\)
Putting in (i)
\(\frac{5}{7}\) R₂ + R₂ = 1800 × 9.8
R₂ = \(\frac{7 \times 1800 \times 9.8}{12}\)
= 10290 N
R₁ = \(\frac{5}{7}\) R₂
= \(\frac{5}{7}\) × 10290
= 7350 N.

Question 10.
(a) Find the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be 2 MR²/5. where M is the mass of the sphere and R is the radius of the sphere.
Solution:
a) Moment of inertia of sphere about any diameter = \(\frac{2}{5}\)MR²
Applying theorem of parallel axes,
Moment of inertia of sphere about a tangent to the sphere = \(\frac{2}{5}\)MR² + M(R)²
= \(\frac{7}{5}\)MR².

(b) Given the moment of inertia of a disc of mass M and radius R about any of its diameters to be MR²/4, find its moment of inertia about an axis normal to the disc and passing through a point on its edge.
Solution:
We are given, moment of inertia of the disc about any of its diameters = \(\frac{1}{4}\)MR².
i) Using theorem of perpindicular axes, moment of inertia of the disc about an axis passing through its center and normal to the disc = 2 × \(\frac{1}{4}\)MR² = \(\frac{1}{2}\)MR²
ii) Using theorem of parallel axes, moment of inertia of the disc passing through a point on its edge and normal to the disc
= \(\frac{1}{2}\)R² + MR² = \(\frac{3}{2}\) MR².

Question 11.
Torques of equal magnitude are applied to a hollow cylinder and a solid sphere, both having the same mass and radius. The cylinder is free to rotate about its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its centre. Which of the two will acquire a greater angular speed after a given time.
Solution:
If M is mass and R is radius of the hollow cylinder and the solid sphere, then
M.I of hollow cylinder about its axis of symmetry I₁ = MR² and
M.I of solid sphere about an axis through its 2 , centre, I₁ = \(\frac{2}{5}\) MR²
Torque applied, I = I₁ α₁ = I₂ α₂
\(\frac{\alpha_2}{\alpha_1}=\frac{l_1}{l_2}=\frac{M^2}{\frac{2}{5} M R^2}=\frac{5}{2}\)
α₂ > α₁
From ω = ω₀ + αt, we find that for given ω₀ and t, ω₂ > ω₁ to, i.e. angular speed of solid sphere will be greater than angular speed of hallow sphere.

Question 12.
A solid cylinder of mass 20 kg rotates about its axis with angular speed 100 rad s^-1. The radius of the cylinder is 0.25m. What is the kinetic energy associated with the rotation of the cylinder ? What is the magnitude of angular momentum of the cylinder about its axis ?
Solution:
Here, M = 20 kg, R = 0.25 m, w – 100 g^-1
Moment of inertia of solid cylinder
= \(\frac{\mathrm{MR}^2}{2}=\frac{20 \times(0.25)^2}{2}\) = 0.625 kg/m²
K.E of rotation = \(\frac{1}{2}\) Iω² = \(\frac{1}{2}\) × 0.625 × (100)² = 3125 J
Angular momentum, L = Iω
= 0.625 × 100
= 62.5 Js.

Question 13.
a) A child stands at the centre of a turntable with his two arms outstretched. The turntable is set rotating with an angular speed of 40 rev/miri. How much is the angular spped of the child if he folds his hands back and thereby reduces his moment of inertia to 2/5 times the initial value ? Assume that the turntable rotates without friction.
Solution:
Here, intial angular speed ω₁ = 40 rev/min, ω₂ = ?
Final moment of inertia, I₂ = \(\frac{2}{5}\)I, Intial moment of Inertia
As no external torque acts in the process, therefore
Iω = constant
i.e. I₂ω₂ = I₁ω₁
ω₂ = \(\frac{I_1}{I_2}\) ω₁ = \(\frac{5}{2}\) × 40
= 100 rpm

b) Show that the child’s new kinetic energy of rotation is more than the initial kinetic energy of rotation. How do you account for this increase in kinetic energy ?
Solution:
Final K.E of rotation, E₂ = \(\frac{1}{2}\)I₂ω₂²
Intial K.E of rotation, E₁ = \(\frac{1}{2}\)I₂ω₁²
\(\frac{E_2}{E_1}=\frac{\frac{1}{2} l_2 \omega_2^2}{\frac{1}{2} l_1 \omega_1^2}=\left(\frac{l_2}{l_1}\right)\left(\frac{\omega_2}{\omega_1}\right)^2\)
= \(\frac{2}{5} \times\left(\frac{100}{40}\right)^2=\frac{5}{2}\) = 2.5
∴ K.E of rotation increase. This is because child spends internal energy folding back his hands.

Question 14.
A rope of negligible mass is wound roung a hollow cylinder of mass 3kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N ? what is the linear acceleration of the rope ? Assume that there is no slipping.
Solution:
Here M = 3kg, R = 40 cm = 0.4 m
Moment of Inertia of the hollow cylinder about its axis
I = MR² = 3(0.4)² = 0.48 kgm²
Force applied F = 30 N
∴ Torque, τ = F × R = 30 × 0.4 = 12 N – m.
If α is the angular acceleration, produced, then from τ = Iα
α = \(\frac{\tau}{\mathrm{I}}=\frac{12}{0.48}\) = 25 rads^-2
Linear acceleration, a = Rα = 0.4 × 25 = 10 m/s².

Question 15.
To maintain a rotor at a uniform angular speed of 200 rad s^-1, an engine needs to transmit a torque of 180 N m. What is the power required by the engine ? (Note : uniform angular velocity in the absence of friction implies zero torque. In practice, applied torque is needed to counter frictional torque). Assume that the engine is 100% efficient.
Solution:
Here, ω = 200 rad/s, torque τ = 180 N – m, power p = ?
As p = τω
∴ p = 180 × 200 = 3600 watt = 36 kw.

Question 16.
From a uniform disc of radius R, a circular hole of radius R/2 is cut out. The centre of the hole is a R/2 from the centre of the original disc. Locate the centre of gravity of the resulting flat body.
Solution:
Suppose mass per unit area of the disc = M
∴ Mass of original disc

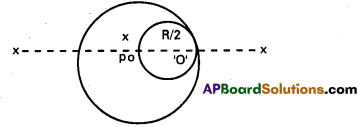
M = πR² × m
Mass of portion removed from the disc
M’ = π\(\left(\frac{R}{2}\right)^2 \times m=\frac{\pi R^2}{4} m=\frac{M}{4}\)
In fig, mass M is connected at O and mass
M’ is concentrated at O’, where OO’ = \(\frac{\mathrm{R}}{\mathrm{2}}\).
After the circular disc of mass M’ is removed, the remaining portion can be considered as a system of two masses M at 0 and – M’ = \(\frac{\mathrm{-M}}{\mathrm{4}}\) at O’. If x is the distance of centre of 4 mass (p) of the remaining part, then
x = \(\frac{M \times O-M^{\prime} \times \frac{R}{2}}{M-M^{\prime}}\)
= \(\frac{\frac{-M}{4} \times \frac{R}{2}}{M-\frac{M}{4}}=\frac{-M R}{8} \times \frac{4}{3 M}=\frac{-R}{6}\)
Negative sign shows that p is the left O.

Question 17.
A metre stick is balanced on a knife edge at its centre. When two coins, each of mass 5g are put one on top of the other at the 12.0 cm mark, the stick is found to be balanced at 45.0 cm. What is the mass of the metre stick ?

Solution:
Let m be the mass of stick concentrated at c, the 50 cm, mark,
For equilibrium about c’ the 45 cm mark,
10g (45 – 12) = mg(50 – 45)
10 g × 33 = mg × 5
m = \(\frac{10 \times 33}{5}\)
= 66 gram.

Question 18.
A solid sphere rolls down two different inclined planes of the same heights but different angles of inclination, (a) Will it reach the bottom with the same speed in each case ? (b) Will jt take longer to roll down one plane than the other ? (c) If so, which one and why ?
Solution:
Let v be the speed of the solid sphere at the bottom of the incine. Applying principle of conservation of energy, we get
\(\frac{1}{2}\) mv² + \(\frac{1}{2}\) Iω² = mgh
As I = \(\frac{2}{5}\) mr²; \(\frac{1}{2}\) mv² + \(\frac{1}{2}\) (\(\frac{2}{5}\) mr²)ω² = mgh
as rω = v, \(\frac{1}{2}\) mv² + \(\frac{1}{5}\) mv² = mgh
v = \(\sqrt{\frac{10}{7} \mathrm{gh}} .\)
As h is same in two cases, v must be same i.e., It will reach the bottom with the same speed. Time taken to roll down the two planes will also be the same, as their height is the same.

Question 19.
A hoop of radius 2 m weighs 100 kg. It rolls along a horizontal floor so that its centre of mass has a speed of 20 cm/s. How much work has to be done to stop it ?
Solution:
Here, R = 2m, M = 100 kg v = 20 cm/s = 0.2 m/s.
Total energy of the hoop = \(\frac{1}{2}\) mv² + \(\frac{1}{2}\) Iω²
= \(\frac{1}{2}\) mv² + \(\frac{1}{2}\) (MR)²ω² = \(\frac{1}{2}\) mv² + \(\frac{1}{2}\) mv²
= mv².
Work required to stop the hoop = total energy of the hoop
w = mv² = 100(0.2)² = 4 joule.

Question 20.
The oxygen molecule has a mass of 5.30 × 10^-26 kg and a moment of inertia of 1.94 × 10^-46 kg m² about an axis through its centre perpendicular to the lines joining the two atoms. Suppose the mean speed of such a molecule in a gas is 500 m/s and that its kinetic energy of rotation is two thirds of its kinetic energy of trans-lation. Find the average angular velocity of the molecule.
Solution:
Here, m = 5.30 × 10^-26 kg
I = 1.94 × 10-^-46 . kgm²
v = 500 m/s
If \(\frac{\mathrm{m}}{\mathrm{2}}\) is mass of each atom of oxygen and 2r is the distance between the two atoms as shown in fig. then

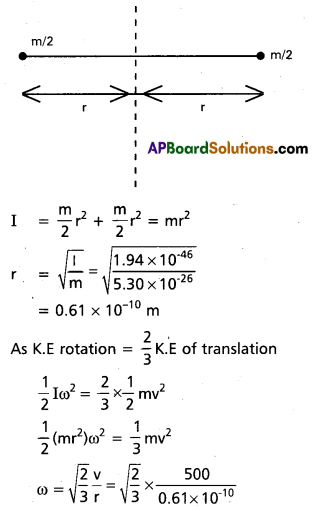
= 6.7 × 10-¹² rod/s.

Question 21.
A solid cylinder rolls up an inclined plane of angle of inclination 30°. At the bottom of the inclined plane the centre of mass of the cylinder has a speed of 5 m/s.
a) How far will the cylinder go up the plane ?
b) How long will is take to return to the bottom ?
Solution:
Here θ = 30°, v = θm/s
Let the cylinder go up the plane upto a height h
From \(\frac{1}{2}\) mv² + \(\frac{1}{2}\) Iω² = mgh
\(\frac{1}{2}\) mv² + \(\frac{1}{2}\) (\(\frac{1}{2}\) mr²) ω² = mgh
\(\frac{3}{4}\) mv² = mgh
h = \(\frac{3 v^2}{4 g}=\frac{3 \times 5^2}{4 \times 9.8}\) = 1.913 m
If s is the distance up the inclined plane, then as sin θ = \(\frac{\mathrm{h}}{\mathrm{s}^2}\)
s = \(\frac{\mathrm{h}}{\sin \theta}=\frac{1.913}{\sin 30^{\circ}}\) = 3.826 m
Time taken to return to the bottom
t = \(\sqrt{\frac{2 s\left(1+\frac{k^2}{r^2}\right)}{g \sin \theta}}=t \sqrt{\frac{2 \times 3.826\left(1+\frac{1}{2}\right)}{9.8 \sin 30^{\circ}}}\) = 1.53 s.

Question 22.
As shown in Fig. the two sides of a step ladder BA and CA are 1.6 m long and hinged at A. A rope DE, 0.5 m is tied half way up. A weight 40 kg is suspended from a point F.1.2 m from B along the ladder BA. Assuming the floor to be frictionless and neglecting the weight of the ladder, find the tension in the rope and forces exerted by the floor on the ladder.
(Take g = 9.8 m/s²)

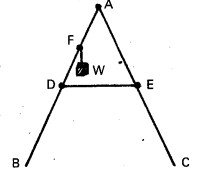
(Hint: Consider the equilibrium of each side of the ladder separately.)
Solution:
Data seems to be insufficient

Question 23.
A man stands on a rotating platform, with his arms stretched horizontally holding a 5 kg weight in each hand . The angular speed of the platform is 30 revolutions per minute. The man then brings his arms dose to his body with the distance of each weight from the axis changing from 90cm to 20 cm. Thd moment of inertia of the man together with the platform may be taken to be constant and equal to 7.6 kg m²
(a) What is his new angular speed ? (Neglect friction.)
b) Is kinetic energy conserved in the process ? If not, form where does the change come about ?
Solution:
Here l₁ = 7.6 × 2 × 5(0.9)² = 15.7 kgm²
ω₁ = 30 rpm
l₂ = 7.6 + 2 × 5(0.2)² = 8.0 kgm²
ω₂ = ?
According to the principle of conservation of angular momentum
l₂ω₂ = l₁ω₁
ω₂ = \(\frac{l_1}{l_2} \omega_1=\frac{15.7 \times 30}{8.0}\) = 58.88 rpm

Question 24.
A bullet of mass 10 g and speed 500 m/s is fired into a door and gets embedded exactly at the centre of the door. The door is 1.0 m wide and weighs 12 kg. It is hinged at one end and rotates about a vertical axis practically without friction. Find the angular speed of the door just after the bullet embeds into it.
(Hint : The moment of inertia of the door about the vertical axis at one end is ML²/3.)
Solution:
Angular momentum imparted by the bullet
I_ = mv × r = (10 × 10^-3) × 500 × \(\frac{1}{2}\) = 2.5
Also, L = \(\frac{M L^2}{3}=\frac{12 \times 1.0^2}{3}\) = 4kgm
As L = Lω
∴ ω = \(\frac{\mathrm{L}}{1}=\frac{2.5}{4}\) = 0.625 rad/sec.

Question 25.
Two discs of moments of inertia I, and I2 about their respective axes (normal to the disc and passing through the centre), and rotawing with angular speeds ω₁, and ω₂ are brought into contact face to face with their axes of rotation coincident,
(a) .What is the angular speed of the two-disc system ?
(b) Show that the kinetic energy of the combined system is less than the sum of the initial kinetic energies of the two discs. How do you account for this loss in energy ? Take ω₁ ≠ ω₁.
Solution:
Here, total intial angular momentum of the two discs L₁ = I₁ω₁ + I₂ω₂
Under, the given conditions, moment of intertia of the two disc system = (I₁ + I₂)
If ω is angular speed of the combined system, the final angular momentum of the system
L₂ = (I₁ + I₂)ω
As no external torque is involved in this excercise, therefore, L₂ = L₁
(I₁ + I₂)ω = I₁ω₁ + I₂ω₂
ω = \(\frac{I_1 \omega_1+I_2 \omega_2}{I_1+I_2}\)

b) Initial K.E of two disc E₁ = \(\frac{1}{2}\) I₁ω₁² + \(\frac{1}{2}\) I₂ω₂²
Final K.E of the system E₂ = \(\frac{1}{2}\) (I₁ + I₂)ω²

∴ E₁ – E₂ > 0 or E₁ > E₂ or E₂ < E₁
Hence there occurs a loss of K.E in the process. Loss of energy = E₁ – E₂. This loss must be due to friction in the contact of the two discs.

Question 26.
a) Prove the theorem of perpendicular axes.
(Hint: Square of the distance of a point (x, y) in the x – y plane from an axis through the origin and perpendicular to the plane is x² + y²).
Answer:
Statement: The sum of moments of inertia of a plane lamina about any two perpendicular axes in its plane is equal to its moment of inertia about an axis perpendicular to the plane and passing through the point of intersection of the first two axes.

Proof : Consider a plane lamina revolving about the Z axis. Let ‘O’ be the origin of the axis. Imagine a particle of mass ‘m’ lying at a distance ‘r’ from point ‘o’ on the plane. Let x, y be the coordinates of the point P.
Thus r² = x² + y²
Then the moment of the body about x-aixs
I_x = Σm y²
The moment of inertia of the body about y-axis.
I_y = Σm x²
Then the moment of inertia of the body about Z-axis

I_z = Σm r²
I_z = Σm(x² + y²)
I_z = Σm x² + Σm y² = I_y + I_x
∴ I_z = I_x + I_y
Hence perpendicular axes theorem is proved.

b) Prove the theorem of parallel axes.
(Hint: If the centre of mass is chosen to be the origin Σm_ir_i = 0).
Answer:
Statement: The moment of inertia of a plane lamina about an-axis is equal to the sum of the moment of inertia about a parallel axis passing through the centre of mass and the product of its mass and square of the distance between the two axes i.e., I₀ = I_G + Mr²
Let I_G is the moment of inertia of the plane lamina about the axis Z₂ passing through the centre of mass.
I₀ is the moment of inertia of the plane lamina about an axis Z₁
Let M be the mass of the lamina and r be the distance between the two axes . Then
I₀ = I_G + mr².
Proof : Let a particle of mass m is situated at P. Moment of inertia about the axis passing through 0 is
dl = m op² or I = Σm op².
Join the lines PO and PG and draw the line PQ and Join with the line extending from OG.
From the trainagle POQ, OP² = OQ² + PQ²
OP² – (OG + GQ)² + PQ² + OQ = OG + GQ
OP² = OG² + 2OG . GQ + (GQ² + PQ²)
OP² – OG² + 2OG. GQ + GP²
OP² = OG² + GP² + 2OG.GQ
[∵ From the ∆le PGQ, GP² = PQ² + GQ²]

Multiplying with Σm on both side
Σm OP² = Σm OG² + Σm GP² + Σm OG. GQ
But Σm OG² = Mr²
(∵ OG is constant and Σm = M, total mass of the body)
Σm GP² = I_G
Σm OP² = I₀
∴ I₀ = Mr² – I_G + 2r ΣmGQ
Σm.GQ = 0
[∵ The moment of all the particles about the centre of mass is always zero]
I₀ = I_G + Mr²
Thus the theorem is proved.

Question 27.
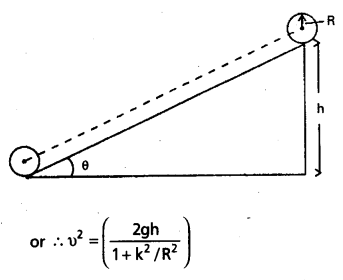
Prove the result that the velocity u of translation of a rolling body (like a ring, disc, cylinder or sphere) at the bottom of an inclined plane of a height h is given by υ² = \(\frac{2 g h}{\left(1+k^2 / R^2\right.}\) using dynamical consideration (i.e. by consideration of forces and torques). Note k is the radius of gyration of the body about its symmetry axis, and R is the radius of the body. The body starts from rest at the top of the plane.
Solution:
When a body rolls down an incline of height h, we apply the principle of conservation of energy.

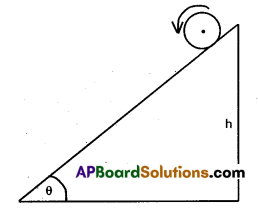
K.E of translation + K.E of rotation = P.E at the top
i.e . \(\frac{1}{2}\) mv² + \(\frac{1}{2}\) Iω² = mgh
\(\frac{1}{2}\) mv² + \(\frac{1}{2}\) (mk²) ω² = mgh
As w = \(\frac{\mathrm{V}}{\mathrm{R}}\)
∴ \(\frac{1}{2}\)mv² + \(\frac{1}{2}\)m \(\frac{k^2}{R^2}\)v² = mgh
or mv² (1 + \(\frac{k^2}{R^2}\)) = mgh
v² = \(\frac{2 g h}{\left(1+\frac{K^2}{R^2}\right)}\)

Question 28.
A disc rotating about its axis with angular speed ω₀ is placed lightly (without any translational push) on a perfectly frictionless table. The radius of the disc is R. What are the linear velocities of the points A, B and C on the disc shown in Fig. ? Will the disc roll in the direction indicated ?

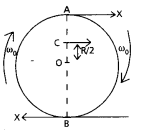
Solution:
Using the reaction v = rω,
we get
for point A, V_A = Rω₀, along AX
for point B, V_B = Rω₀, along BX
for point C, V_c = (\(\frac{\mathrm{R}}{\mathrm{2}}\) ω₀ parallel to AX,
The disc will not rotate, because it is placed on a perfectly frictionless table, without, rolling is not possible.

Question 29.
Explain why friction is necessary to make the disc in Figure roll in the direction indicated.

(a) Give the direction of frictional force at B and the sense of frictional torque before perfect rolling begins.
(b) What is the force of friction after perfect rolling begins ?
Solution:
To roll a disc, we require a torque, which can be proved only by a tangential force. As force of friction is the only tangential force in this case, it is necessary.
(a) As frictional force at B opposes the velocity of point B, which is to the left, the frictional force must be to the right. The sense of frictional torque will be perpendicular to the plane of the disc and outwards.

(b) As frictional force at B decreases the velocity of the point of contact B with the surface, the perfect rolling begins only when velocity of point B becomes zero. Also, force of friction would become zero at this stage.

Question 30.
A solid disc and a ring, both of radius 10 cm are placed on a horizontal table simultaneously, with initial angular speed equal to 10 π rad s^-1. Which of the two will start to roll earlier ? The co-efficient of kinetic friction is μ_k = 0.2.
Solution:
Here, intial velocity of centre of mass is zero i.e, u = 0.
Frictional force causes the GM to accelerate
μ_k mg = ma ∴ a = μ_k g
As v = u + at ∴ v = 0 + μ_k gt
Torque due to friction causes retardation in the intial angular speed ω₀.
i.e. μ_k mg × R = – Iα
α = \(\frac{\mu_k \mathrm{mgR}}{\mathrm{I}}\)
ω = ω₀ + αt
∴ ω = ω₀ – \(\frac{\mu_k \mathrm{mgRt}}{\mathrm{I}}\)
Rolling begins, when v = Rω from (ii) and (iv)

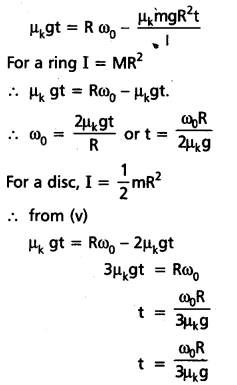
Comparing (vi) and (vii) we find that the disc would begin to roll earlier than the ring We can calculate the values of t from (vi) and (vii) using known values of μ_k, g, R and ω₀.

Question 31.
A cylinder of mass 10kg and radius 15 cm is rolling perfectly on a plane of inclination 30°. The coefficient of static friction μ_s = 0.25.
(a) How much is the force of friction acting on the cylinder?
(b) What is the work done against friction during rolling?
(c) If the inclination θ of the plane is increased, at what value of θ does the cylinder begin to skid, and not roll perfectly?
Solution:
Here, m = 10 kg, r = 15 cm = 0.15 m
θ = 30°, μ_s = 0.25
Accelaration of the cylinder down the incline,
α = \(\frac{2}{3}\)g sin θ = \(\frac{2}{3}\) × 9.8 sin 30° = \(\frac{9.8}{3}\) m/s²
a) Force of friction, f = mg sin θ – ma = m(g sin θ – α) = 10(9.8 sin 30° – \(\frac{9.8}{3}\)) = 16.4 N
b) During rolling the point of contact is at rest. Therefore work done against friction is zero
c) For rolling without slipping/skidding μ = \(\frac{1}{3}\) tan θ
tan θ = 3μ
= 3 × 0.25 = 0.75
θ = 37°.

Question 32.
Read each statement below carefully, and state, with reasons, if it is true or false;
(a) During rolling, the force of friction acts in the same direction as the direction of motion of the CM of the body.
(b) The instantaneous speed of the point of contact during rolling is zero.
(c) The instantaneous acceleration of the point of contact during rolling is zero.
(d) For perfect rolling motion, work done against friction is zero.
(e) A wheel moving down a perfectly italic inclined plane will undergo slipping (not roiling) motion.
Solution:
a) The statement is false.

b) True. This is because rolling body can be imagined to be rotating about an axis passing through the point of contact of the body with the ground.
Hence its instantaneous speed is zero.

c) This is not true. This is because when the body is rotating its instantaneous acc is not zero.

d) It is true. This is because once the perfect rolling begins, force of friction becomes zero. Hence work done against friction is zero.

e) The statement is true. This is because rolling occurs only on account of friction which is tangential force capable of providing torque. When the inclined plane is perfectly smooth it will simply slip under the effect of its own weights.

Question 33.
Separation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass :
(a) Show P = \(\mathrm{P}_{\mathrm{i}}^{-}+\mathrm{m}_{\mathrm{i}} \mathrm{V}\)
Where P_i is the momentum of the i_i the particle (of mass m_i) and p’_i + m_iv’_i. Note relative velocity of the ith particle relative to the centre of mass. Also, prove using the definition of the centre of mass Σp’_i = 0
(b) Show K = K’ + 1/2MV²
Where K is the total kinetic energy of the system of particles. K’ is the total kinetic energy of the system when the particle velocities are taken with respect to the centre of mass and MV²/2 is the kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the system). The result has been used in Sec. 7.14.
(c) Show L = L’ + R × MV
Where L’ = Σr_i P_i is the angular momentum of the system about the centre of mass with velocities taken relative to the centre of mass. Remember r’_i = r_i – R rest of the notation is the standard notation used in the chapter. Note L1 and MR × V can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles.
(d) Show \(\frac{d l^{\prime}}{d t}=\sum r_i^{\prime} \frac{d p^{\prime}}{d t}\)
Further, show that \(\frac{\mathrm{dL}^{\mathrm{l}}}{\mathrm{dt}}\) = τ’_ext
Whereτ’_ext is the sum of all external torques acting on the system about the centre of mass.
(Hint: Use the definition of centre of mass and Newton’s Third Law. Assume the internal forces between any two particles act along the line joining the particles.)
Solution:
a) Let m₁, m₂, … m_i mass points have the position vectors \(\overrightarrow{r_1}, \overrightarrow{r_2}, \overrightarrow{r_i}\) w.r.t origin ‘O’. The position vector of C.M. say \(\overrightarrow{\mathrm{OP}}\)
i.e., \(\overrightarrow{\mathrm{OP}}=\frac{m_1 \overrightarrow{r_1}+m_2 \overrightarrow{r_2}+\ldots}{m_1+m_2+\ldots}=\frac{m_i r_i}{M}\)
where i = 1, 2, 3 .
Now, let us change the origin to O’ and assume that the C.M is now at p’ with

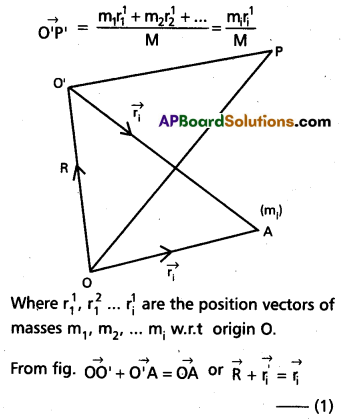
Multiplying eqn. (1) by m_i and differentiating w.r.t to time, we get

even if we change the origin, the position of
centre of mass will not change i.e., Σp’_i = 0

b) In rotational kinematics, K.E_T of the system of particles = K.E_T of the system when the particle velocities are taken w.r.t to CM + K.E of the translation of the system as a whole (i.e. of the C.M motion of the system)
i.e. \(\frac{1}{2}\) m₁v₁² + \(\frac{1}{2}\) m₂v₂² + …..
= [\(\frac{1}{2}\) m₁v₁² + \(\frac{1}{2}\)m₂v₂ +……] + \(\frac{1}{2}\)Mv²
\(\frac{1}{2}\) m_iv_i² = \(\frac{1}{2}\)m_iv_i² + \(\frac{1}{2}\) mv²
∴ k = k’ + \(\frac{1}{2}\)
where M = total mass of particles
and y = velocity of C.M motion of the system.

c) From eq. (1), we have

Textual Examples

Question 1.
Find the centre of mass of three particles at the vertices of an equilateral triangle. The masses of the particles are 100g, 150 g, and 200 g respectively. Each side of the equilateral triangle is 0.5 long. [A.P. & T.S. Mar.18]
Solution:

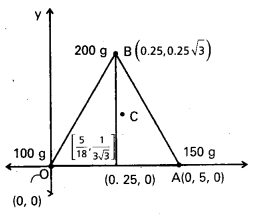
With the x – and y-axes chosen as shown in Fig. 7.9, the coordinates of points O, A and B forming the equilateral triangle are
respectively (0, 0), (0, 5, 0), (0.25. \(\sqrt{3}\) ). Let the masses 100 g, 150g and 200g be located at O, A and B be respectively. Then.

Question 2.
Find the centre of mass of a triangular lamina.
Solution:
The lamina (∆LMN) may be subdivided into narrow strips each parallel to the base (MN) as shown in Fig.

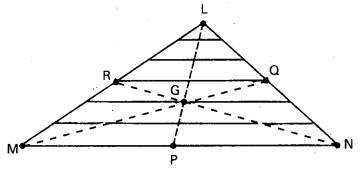
By symmetry each strip has its centre of mass at its midpoint. If we joint the midpoint of all the strips we get the median LP. The centre of mass of the triangle as a whole therefore, has to lie on the median LP. Similarly, we can argue that it lies on the median MQ and NR. This means the centre of mass lies on the point of concurrence of the medians, i.e. on the centroid G of the triangle.

Question 3.
The density of the atmosphere at sea level is 1.29 kg/m³. Assume that it does not change with altitude. Then how high would the atmosphere extend ?
Solution:
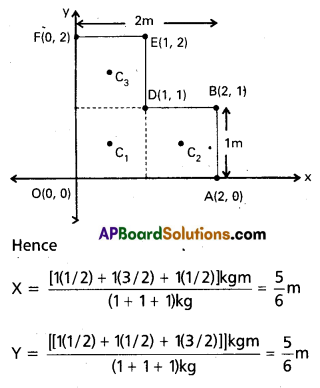
The centres of mass C₁, C₂ and C₃ of the squares are, by symmetry, their geometric centres and have coordinates (1/2,1/2), (3/ 2,1/2), (1/2,3/2) respectively.

Question 4.
A 3m long ladder weighing 20 kg leans on a frictionless wall. Its feet reston the floor 1 m from the wall as shown in Fig. Find the reaction forcesof the wall and the floor.
Solution:

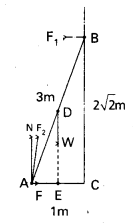
Let AB is 3 m long, A is at distance AC = 1 m from the wall. Pythagoras theorem,
BC = 2\(\sqrt{2}\) m.
For translational equilibrium, taking the forces in the vertical direction, N – W = 0 ……….. (i)
Taking the forces in the horizontal direction,
F – F₁ = 0 ……………. (ii)
taking the moments of the forces about A,
2\(\sqrt{2}\) F1 – (1/2) W = 0 ………….. (iii)
Now W = 20 g = 20 × 9.8 N = 1960.0 N
From (i) N = 196.0
From (iii) = F₁ = W/4 \(\sqrt{2}\) = 196.0/4 \(\sqrt{2}\)
= 34.6 N
From (ii) F = F₁ = 34.6 N
F₂ = \(\sqrt{F^2+N^2}\) = 199.0 N

Question 5.
Find the scalar and vector products of two vectors
a = \((3 \vec{i}-4 \vec{j}+5 \vec{k})\) and b = \((-2 \vec{i}+\vec{j}-3 \vec{k})\)
Solution:
a.b = (\((3 \vec{i}-4 \vec{j}+5 \vec{k})\)) . (\((-2 \vec{i}+\vec{j}-3 \vec{k})\))
= -6 – 4 – 15 = -25
a × b = \(\left|\begin{array}{ccc}
\vec{i} & \vec{j} & \vec{k} \\
3 & -4 & 5 \\
-2 & 1 & -3
\end{array}\right|=7 \vec{i}-\vec{j}-5 \vec{k}\)
Note b × a = \(7 \vec{i}-\vec{j}-5 \vec{k}\)

Question 6.
Obtain Equation from first principles.
Solution:
The angular acceleration is uniform,
ω = αt + c (as α is comstant)
At t = 0, ω = ω₀ (given)
From (i) we get at t = 0, ω = c = ω₀
Thus, ω = αt + ω₀ as required

Question 7.
The angular speed of a motor wheel is increased from 1200 rpm to 3120 rpm is 16 seconds, (i) What is its angular acceleration, assuming the acceleration to be uniform ? (ii) How many revolutions does the engine make during this time ?
Solution:
(i) We shall use ω = ω₀ + αt
ω₀ = initial angular speed in rad/s
= 2π × angular speed in rev/s
= \(\frac{2 \pi \times \text { angular speed in rev } / \mathrm{min}}{60 \mathrm{~s} / \mathrm{min}}\)
= \(\frac{2 \pi \times 1200}{60} \mathrm{rad} / \mathrm{s}\)
= 40π rad/ s
Similarly ω = final angular speed in rad /s
= \(\frac{2 \pi \times 3120}{60} \mathrm{rad} / \mathrm{s}\)
= 2π × 52 rad/s = 104 π rad/s
∴ Angular acceleration
α = \(\frac{\omega-\omega_0}{t}\) = 4π rad/s²
The angular acceleration of the engine = 4π rad/s²

(ii) The angular displacement in time t is given by
θ = ω₀t + \(\frac{1}{2}\) αt²
= (40π × 16 + \(\frac{1}{2}\) × 4π × 16²) rad
= (640 π+ 512 π )rad
= 1150π rad
Number of revolutions = \(\frac{1152 \pi}{2 \pi}\) = 576

Question 8.
Find the torque of a force \((\bar{i}-\bar{j}+\bar{k})\) about the origin. The force acts on a particle whose position vector is \((\bar{i}-\bar{j}+\bar{k})\) (Mar.’14, 13)
Answer:
Here r = \(\vec{i}-\vec{j}+\vec{k}\)
and F = \(7 \vec{i}-3 \vec{j}+5 \vec{k}\)
We shall use the determinant rule to find the torque τ = r × F
τ = \(\left|\begin{array}{ccc}
\vec{i} & \vec{j} & \vec{k} \\
1 & -1 & 1 \\
7 & 3 & -5
\end{array}\right|=(5-3) \vec{i}-(-5-7) \vec{j}\) + \((3-(-7)) \vec{k}\)
or τ = \(2 \vec{i}+12 \vec{j}+10 \vec{k}\)

Question 9.
Show that the angular momentum about any point of a single particle moving with constant velocity remains constant throughout the motion.
Solution:
Let the particle with velocity v be at point P at some instant t. We want to calculate the angular momentum of the particle about an arbitrary point O.

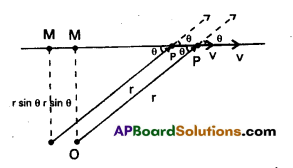
The angular momentum is 1 = r × mv. Its magnitude is mvr. sine, where θ is the angle between r and v as shown in Fig. Although the particle changes position with time, the line of direction of v remains the same and hence OM = r sin θ ; a constant.

Question 10.
Show that moment of a couple does not depend on the point about which you take the moments.
Solution:

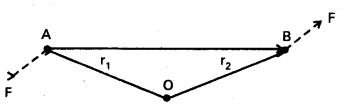
The moment of the couple = sum of the moments of the two forces making the couple
= r₁ × (-F) + r₂ × F
= r₂ × F + r₁ × F
= (r₂ – r₁) × F
But r₂ + AB = r₂, and hence AB = r₂ – r₁.
The moment of the couple, therefore, is AB × F.

Question 11.
What is the moment of intertia of a disc about one of its diameters ?
Solution:

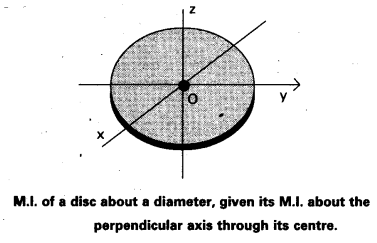
x and y-axes lie in the plane of the disc and z is perpendicular I_z = I_x = I_y
Now, x and y axes are along two diameters of the disc, and by symmetry the moment of inertia of the disc is the same about any diameter. Hence
I_x = I_y
and I_z = 2I_y
But I_x = I_y
So finally, I_x = I_z/2 = MR²/4
Thus the moment of inertia of a disc about any of its diameter is MR²/4.
Find similarly the moment of inertia of a ring about any of its diameter. Will the theorem be applicable to a solid cylinder?

Question 12.
What is the moment of inertia of a rod of mass M, length l about an axis perpendicular to it through one end ?
Solution:
For the rod of mass M and length l, I = Ml²/ 12. Using the parallel axes theorem, I’ = I + Ma² with a = l/2 we get.
I’ = \(\mathrm{M} \frac{l^2}{12}+\mathrm{M}\left(\frac{l}{2}\right)^2=\frac{\mathrm{M} l^2}{3}\)
We can check this independently since I is half the moment of inertia of a rod of mass 2M and length 21 about its midpoint,
I’ = \(2 \mathrm{M} \frac{4 l^2}{12} \times \frac{1}{2}=\frac{\mathrm{M} l^2}{3}\)

Question 13.
What is the moment of inertia of a ring about a tangent to the circle of the ring ?
Solution:
The tangent to the ring in the plane of the ring is parallel to one of the diameters of the ring. The distance between these two parallel axes is R, the radius of the ring. Using the parallel axes theorem.

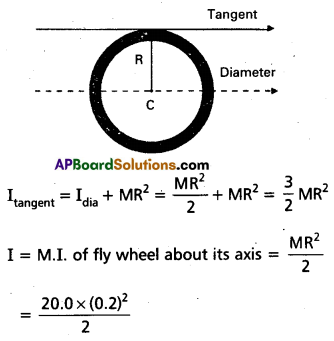
= 0.4kg m²
α = angular acceleration
= 5.0 Nm/0.4 kg m² = 12.5 S^-2

b)Work done by the pull unwinding 2m of the cord
= 25 N × 2 m = 50 J

(c) Let ω be the final angular velocity. The kinetic energy gained = \(\frac{1}{2}\) Iω²
since the wheel starts from rest. Now,
ω₂ = ω²₀ +2αθ, ω₀ = 0
The angular displacement θ = length of unwound string / radius of wheel = 2m / 0.2 m = 10 rad
ω² = 2 × \(\frac{1}{2}\) × 12.5 × 10.0 = 250 (rad/s)²
∴ K.E. gained = \(\frac{1}{2}\) × 0.4 × 250 = 50 J

(d) The answers are the same, i.e. the kinetic energy gained by the wheel work done by the force. There is no loss of energy due to friction.

Question 14.
A cord of negligible mass is wound round the rim of a fly wheel of mass 20 kg and radius 20 cm. A steady pull of 25 N is applied on the cord as shown in Fig. The flywheel is mounted on a horizontal axle -with frictionless bearings.
(a) Compute the angular acceleration of the wheel.
(b) Find the work done by the pull, when 2m of the cord is unwound
(c) Find also the kinetic energy of the wheel at this point. Assume that the wheel starts from rest.
(d) Compare answers to parts (b) and (c).
Solution:

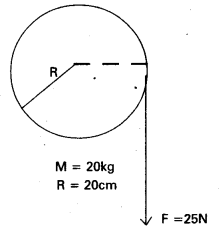
a) We use Iα = τ
the toque τ = FR
= 25 × 0.20 Nm (as R = 0.20m)
= 5.0 Nm

Question 15.
Three bodies, a ring, a solid cylinder and a solid sphere roll down the same inclined plane without slipping. They start from rest. The radii of the bodies are identical. Which of the bodies reaches the ground with maximum velocity ?
Solution:
We assume conservation of energy of the rolling body, i.e. there is no loss of energy due to friction etc. The protential energy lost by the body in rolling down the inclined plane (= mgh) must, therefore, be equal to kinetic energy gained. (See fig.) Since the bodies start from rest the kinetic energy gained is equal tot he final kinetic energy of the odies. From K = \(\frac{1}{2} m v_{\mathrm{cm}}^2\left[1+\frac{\mathrm{k}^2}{\mathrm{R}^2}\right]\)
K = \(\frac{1}{2} m v^2 1+\left(\frac{K^2}{R^2}\right)\) Where v is the final velocity of (the centre of mass of) the body.
Equating K and mgh

Note v² is independent of the mass of the rolling body:
For a ring, k² = R²
v_ring = \(\sqrt{\frac{2 g h}{1+1}}=\sqrt{g h}\)
For a solid cylinder K² = R²/0.2
v_disc = \(\sqrt{\frac{2 g h}{1+1 / 2}}=\sqrt{\frac{4 g h}{3}}\)
For a solid sphere K² = 2R²/5
v_sphere = \(\sqrt{\frac{2 g h}{1+1 / 52}}=\sqrt{\frac{10 g h}{7}}\)