Andhra Pradesh BIEAP AP Inter 1st Year Physics Study Material 8th Lesson Oscillations Textbook Questions and Answers.
AP Inter 1st Year Physics Study Material 8th Lesson Oscillations
Very Short Answer Questions
Question 1.
Give two examples of periodic motion which are not oscillatory.
Answer:
- The motion of planets around the sun.
- The motion of an electron round the nucleus.
Question 2.
The displacement in S.H.M. is given by y = a sin (20t + 4). What is the displacement when it is increased by 2π/ω?
Answer:
The displacement in S.H.M. is y = a sin (20t + 4)
The time period T = \(\frac{2 \pi}{\omega}\) is increased, the displacement of the particle remains the same.
![]()
Question 3.
A girl is swinging seated in a swing. What is the effect on the frequency of oscillation if she stands?
Answer:
Frequency (n) = \(\frac{1}{2 \pi} \sqrt{\frac{g}{l}}\), n ∝ \(\frac{1}{\sqrt{l}}\)
A girl swinging in standing position location of centre of mass shifts upwards l decreases, frequency of oscillation increases.
Question 4.
The bob of a simple pendulum is a hollow sphere filled with water. How will the period of oscillation change, if the water begins to drain out of the hollow sphere ?
Answer:
The period of the pendulum is same, when the bob is hollow (or) completely filled with water. As water flows out from the bob, the centre of gravity of the bob lowered. The pendulum length increases. Hence time period also increases. When the bob becomes empty, again centre of gravity shifts upwards. The pendulum length decreases. The time period also decreases.
Question 5.
The bob of a simple pendulum is made of wood. What will be the effect on the time period if the wooden bob is replaced by an identical bob of aluminum ?
Answer:
Time period (T) = \(2 \pi \sqrt{\frac{l}{g}}\), Time period is independent of mass of the bob.
Hence wooden bob is replaced by an identical aluminium bob, Time period remains constant.
Question 6.
Will a pendulum clock gain or lose time when taken to the top of a mountain.?
Answer:
T ∝ \(\frac{1}{\sqrt{g}}\), At the mountain top, the value of g decreases, hence time period increases i.e. the pendulum will take longer time to complete one vibration. Hence pendulum clock will loose time on the mountain top.
Question 7.
A pendulum dock gives correct time at the equator. Will it gain or lose time if it is taken to the poles ? If so, why ?
Answer:
Time period (T) = \(2 \pi \sqrt{\frac{l}{g}}\)
g value at poles is greater than at equator.
If it is taken to the poles g value increases, time period decreases.
So pendulum clock gains time.
![]()
Question 8.
What fraction of the total energy is K.E when the displacement is one half of a amplitude of a particle executing S.H.M.
Answer:
Total energy (E) = \(\frac{1}{2}\) mω2 A2
Given y = \(\frac{\mathrm{A}}{2}\), Kinetic energy = \(\frac{1}{2}\)mω2(A2 – y2) = \(\frac{1}{2}\) mω2\(\left(A^2-\frac{A^2}{4}\right)\) = \(\frac{3}{4}\) × \(\frac{1}{2}\)mω2A2
K.E = \(\frac{3}{4}\) × E
∴ \(\frac{K \cdot E}{E}\) = \(\frac{3}{4}\)
Question 9.
What happens to the energy of a simple harmonic oscillator if its amplitude is doubled ?
Answer:
Total energy (E) = \(\frac{1}{2}\)mω2A2
Given Amplitude A is doubled
E’ = \(\frac{1}{2}\)mω2(2A)2
E’ = 4 × \(\frac{1}{2}\)mω2A2
E’ = 4E
∴ Energy becomes four times.
Question 10.
Can a simple pendulum be used in an artificial satellite? (T.S. Mar. 16)
Answer:
No, in an artificial satellite acceleration due to gravity is zero. Hence we cannot use simple pendulum in an artificial satellite.
Short Answer Questions
Question 1.
Define simple harmonic motion. Give two examples.
Answer:
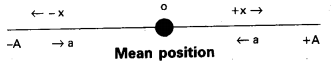
Simple harmonic motion : “A body is said to be in simple harmonic motion, if it moves to and fro along a straight line, about its mean position such that, at any point its acceleration is proportional to its displacement but opposite in direction and is directed always towards the mean position”.
w ∝ -x
If a is the acceleration of the body at any given displacement x from the mean position, the time for the body to be in S.H.M.
Displacement of a particle in S.H.M is given by
x(t) = A cos (ωt + ϕ)
Example:
- Motion of a simple pendulum.
- Motion of mass attached to a spring.
- Motion of atoms in solids.
- Cork floating on water.
![]()
Question 2.
Present graphically the variations of displacement, velocity and acceleration with time for a particle in S.H.M.
Answer:
Let us put ϕ = 0 and write the expressions for x(t),
υ(t) and a(t).
x(t) = A cos ωt. υ(t) = -Aωsinωt
a(t) = -ω2A cos ωt. The corresponding plots are shown in figure. All quantities varies sinusoidally with time.
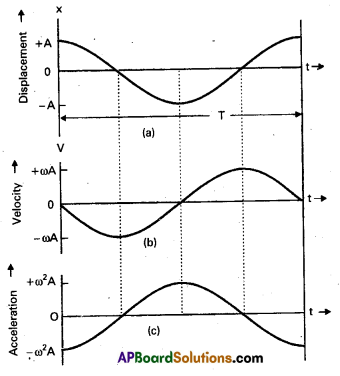
x(t) varies between – A to A; υ(t) varies from -ωA to ωA and a(t) varies from – ω2A to ω2A with respect to displacement plot, velocity plot has a phase difference of \(\frac{\pi}{2}\) and acceleration plot has a phase difference of π.
Question 3.
What is phase ? Discuss the phase relations between displacement, velocity and acceleration in simple harmonic motion.
Answer:
Phase : The phase of a particle executing S.H.M. at any instant is defined as its state (or) condition as regards to its position and direction of motion at that instant.
- Displacement : x = A cos (ωt – ϕ), (ωt – ϕ) is called phase and ϕ is epoch.
- Velocity : V = -Aω sin (ωt – ϕ), Here also (ωt – ϕ) is phase angle
- Acceleration : a = -ω2A cos (ωt – ϕ), Here also (ωt – ϕ) is phase angle.
Phase difference between displacement and velocity = \(\frac{\pi}{2}\)
Phase difference between velocity and acceleration = \(\frac{\pi}{2}\)
Phase difference between displacement and acceleration = π.
Question 4.
Obtain an equation for the frequency of oscillation of spring of force constant k to which a mass m is attached. Answer:
Let us consider a spring suspended vertically from a rigid support and loaded with a mass m. If it is now pulled down and released, it executes vertical oscillations about mean position.
Restoring force is directly proportional to the displacement, but oppositely directed
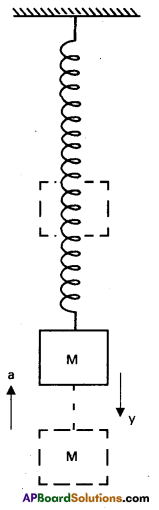
F ∝ -y
F = -ky —–> (1)
Where k is force constant
Ma = -ky (∴ F = Ma)
a = \(-\left(\frac{K}{M}\right) y\) —-> (2)
Since K and M are constant. We can write a ∝ -y
ie Acceleration is directly proportional to the displacement but oppositely directed. Hence oscillations of a loaded spring is S.H.M.
Comparing eq. (2) with a = -ω2y
ω2 = \(\frac{K}{M}\) ; ω = \(\sqrt{\frac{\mathrm{K}}{\mathrm{M}}}\)
T = \(\frac{2 \pi}{\omega}\) ; T = \(2 \pi \sqrt{\frac{\mathrm{M}}{\mathrm{K}}}\)
Frequency of oscillation (n) = \(\frac{1}{2 \pi} \sqrt{\frac{K}{M}}\) —> (3)
Question 5.
Derive expressions for the kinetic energy and potential energy of a simple harmonic oscillator.
Answer:
Kinetic energy of simple harmonic oscillator : The velocity of a particle in S.H.M. is given by
v = \(\omega \sqrt{A^2-y^2}\) ∴ Kinetic energy = \(\frac{1}{2}\) mv2 = \(\frac{1}{2}\) mω2(A2 – y2)
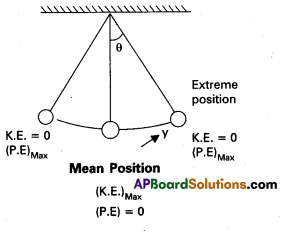
When y = 0, (K.E)Max = \(\frac{1}{2}\) mω2A2 (Mean position)
When y = A, (K.E)Min = 0 (Extreme position)
K.E is maximum at mean position and minimum at extreme position.
Potential energy of simple harmonic oscillator: When the displacement of a particle executing simple Harmonic oscillations increases, the restoring force also increases. The restoring force is in the opposite direction to the displacement. Therefore work is done in moving through the displacement, against restoring force. If F is the restoring force at the displacement y.
The average force against which work is done = \(\frac{\mathrm{O}+\mathrm{F}}{2}\) = \(\frac{F}{2}\)
∴ Workdone on the particle for the displacement (y) = Average force × displacement F
i.e. w = \(\frac{\mathrm{F}}{2}\) × y
w = \(\frac{\max y}{2}\) —- (1) (∵ F = ma)
But acceleration of a particle in S.H.M. is given by
a = ω2y —– (2)
Using eq’s (1) and (2). we get
The work done (w) = \(\frac{1}{2} m \omega^2 y^2\) mw2y2
This work done is stored in the form of P.E.
∴ P.E. = \(\frac{1}{2} m \omega^2 y^2\) —– (3)
If y = 0, (P.E)Min = 0 (At mean position)
If y = A, (P.E)Max = \(\frac{1}{2} m \omega^2 A^2\) (At extreme position).
∴ P.E. is maximum at extreme position and minimum at mean position.
Question 6.
How does the energy of a simple pendulum vary as it moves from one extreme position to the other during its oscillations?
Answer:
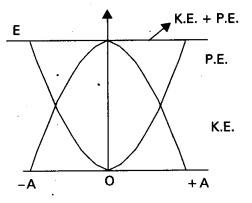
The total energy associated with a particle executing S.H.M. at any point is the sum of potential energy and kinetic energy at that point.
Total energy (E) = K.E + P.E
K.E = \(\frac{1}{2} m \omega^2\left(A^2-y^2\right)\)
P.E. = \(\frac{1}{2} m \omega^2 y^2\)
T.E. = \(\frac{1}{2}\)mω2(A2 – y2) + \(\frac{1}{2}\)mω2y2 = \(\frac{1}{2}\)mω2A2
At mean position y = 0, P.E = 0
and (K.E)Max = \(\frac{1}{2} m \omega^2 A^2\)
∴ T.E. = 0 + \(\frac{1}{2} m \omega^2 A^2\) = \(\frac{1}{2} m \omega^2 A^2\)
At extreme position y = A, K.E = 0 and P.E = \(\frac{1}{2} m \omega^2 A^2\)
∴ (P.E)Max = \(\frac{1}{2} m \omega^2 A^2\)
From mean position to extreme position K.E. is to be converted into P.E.
![]()
Question 7.
Derive the expressions for displacement, velocity and acceleration of a particle executes S.H.M.
Answer:
Consider a particle P moves on the circumference of a circle of radius A with uniform angular velocity ω. Let PN be the perpendicular drawn to the diameter yy’ from P.
As P moves on the circumference of the circle, N moves on the diameter yy’ to and fro about the centre O.
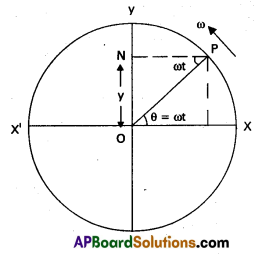
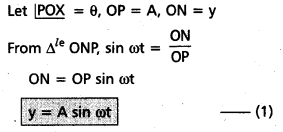
Velocity : The velocity of a partcile executing SHM is given by
v = \(\frac{d y}{d t}\) = \(\frac{\mathrm{d}}{\mathrm{dt}}\) (A sin ωt)
= Aω cos ωt = Aω\(\sqrt{1-\sin ^2 \omega t}\)
v = \(A \omega \sqrt{1-\left(\frac{y}{A}\right)^2}\) (∵ sin ωt = \(\frac{y}{A}\))
v = ω\(\omega \sqrt{A^2-y^2}\) —- (2)
Acceleration : As the rate of change of velocity gives acceleration of the particle executing S.H.M is given by
a = \(\frac{d v}{d t}\) = \(\frac{\mathrm{d}}{\mathrm{dt}}\)(Aω cos ωt) = -Aω2 sin ωt
∴ a = -ω2y —- (3)
Long Answer Questions
Question 1.
Define simple harmonic motion. Show that the motion of (point) projection of a particle performing uniform circular motion, on any diameter, is simple harmonic. (AP – Mar. ‘18; TS – Mar. ‘16)
Answer:
Simple harmonic motion : A body is said to be in simple harmonic motion, if it moves to and fro along a straight line, about its mean position such that, at any point its acceleration is proportional to its displacement but opposite in direction and directed always towards the mean position.
Show that the projection of uniform circular motion on any diameter is simple harmonic : Consider a particle P moving on the circumference of a circle of radius A with uniform angular velocity ω. Let O be the centre of the circle. XX’ and YY’ are two mutually perpendicular diameters of the circle as shown in the figure. Let PN be drawn perpendicular to the diameter YY’ from P. As P moves on the circumference of the circle, N moves on the diameter YY’ to and fro about the centre O. Let us consider the position of N at any time t, after leaving the point ‘O’, during its motion. The corresponding angular displacement of the particle P is ![]()
Hence acceleration is directly proportional to the displacement and opposite direction. Hence motion of N is simple harmonic.
Question 2.
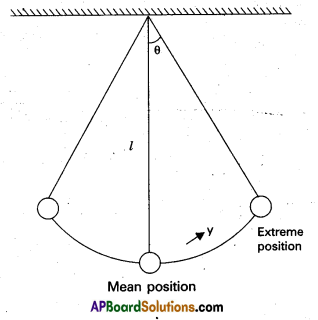
Show that the motion of a simple pendulum is simple harmonic and hence derive an equation for its time period. What is seconds pendulum ? (TS – Mar. ’18, ’17, ’15, ’14, ’13; AP – Mar. ’17, ’16, ’15, ’14, ’13)
Answer:
- Consider simple pendulum, a small bob of mass m tied to an inextensible mass less string of length L and other end of the string is fixed from a rigid support.
- Once the bob is slightly displaced and released, it begins to oscillate about mean position.
- Let θ be the angular displacement and T be the tension in the string.
- The forces acting on the bob are (a) tension T along the string (b) weight mg acts vertically downwards.
- The force mg can be resolved into two components (1) mg cos θ along the PA and (2) mg sin θ acts along PB.
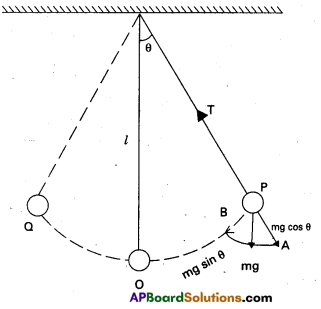
- From figure at point P,
T = mg cos θ —– (1) - The force mg sin θ will provide the restoring torque, which tends to bring the bob back to its mean position O.
- The restoring torque is given by
\(\tau\) = Restoring force × ⊥lar distance
\(\tau\) = -mg sin θ × L —– (2)
Here negative sign shows that the torque acts to reduce θ.
Then sin θ is replaced by θ i.e., sin θ ≈ θ
x = -mg L θ —– (3) (∵ sin θ = θ – \(\frac{\theta^3}{3 !}\) + \(\frac{\theta^3}{5 !}\) …..) - From equation (3), we note that \(\tau\) ∝ θ. and This \(\tau\) will bring the bob back towards its equilibrium position.
So, if the bob is left free, it will execute angular simple harmonic motion.
Comparing equation (3), with the equation \(\tau\) = -kθ, we have Spring factor, k = mgL. - Here inertia factor = Moment of inertia of the bob about the point of suspension = mL2
- In S.H.M, Time period (T) = \(2 \pi \sqrt{\frac{\text { Inertia factor }}{\text { Spring factor }}}\)
T = \(2 \pi \sqrt{\frac{m L^2}{m g L}}\)
T = \(2 \pi \sqrt{\frac{L}{g}}\) — (4)
Seconds pendulum : A pendulum whose time period is 2 seconds is called seconds pendulum.
T = 2 seconds.
![]()
Question 3.
Derive the equation for the kinetic energy and potential energy of a simple harmonic oscillator and show that the total energy of a particle in simple harmonic motion is constant at any point on its path.
Answer:
Kinetic energy : The velocity of a particle in S.H.M is given by v = ω\(\sqrt{A^2-y^2}\)
∴ Kinetic energy = \(\frac{1}{2} \mathrm{mv}^2\) = \(\frac{1}{2} m \omega^2\left(A^2-y^2\right)\) —— (1)
We know that y = A sin ωt
K.E = \(\frac{1}{2}\)mω2A2[1 – sin2ωt) —— (2)
When y = 0, (K.E)Max = –\(\frac{1}{2}\)mω2A2 (Mean position)
When y = A, (K.E)Min = 0 (At extreme position)
∴ K.E is maximum at mean position and minimum at extreme position.
Potential energy : When the displacement of a particle executing simple harmonic oscillations increase, the restoring force also increases. The restoring force is in the opposite direction to the displacement. Therefore work is done in moving through the displacement, against restoring force. If F is restoring force at the displacement y.
The average force against which work is done = \(\frac{\mathrm{O}+\mathrm{F}}{2}\) = \(\frac{F}{2}\)
∴ Workdone on the particle for the displacement (y) = Average force × displacement.
i.e., w = \(\frac{1}{2}\) × y
w = \(\frac{\max y}{2}\) —– (3) (∵ F = ma)
But acceleration of a particle in S.H.M is given by
a = -ω2y —– (4)
Using equations (3) and (4), we get
The work done (W) = \(\frac{1}{2}\)mω2y2
This work done is stored in the form of P.E
∴ P.E = \(\frac{1}{2}\)mω2y2 —– (5)
∴ P.E = \(\frac{1}{2}\)mω2A2 sin2ωt —– (6) (∵ y = A sin ωt)
If y = 0, (P.E)Min = 0 (At mean position)
If y = A, (P.E)Max = – \(\frac{1}{2}\)mω2A2 (At extreme position)
∴ P.E. is maximum at extreme position and minimum at mean position.
Total energy (E) : The total energy associated with a particle executing S.H.M at any point is the sum of RE and K.E at that point.
Total energy (E) = K.E + P.E
K.E. = \(\frac{1}{2}\)mω2y2
∴ T.E. = \(\frac{1}{2}\)mω2 (A2 – y2) + \(\frac{1}{2}\)mω2y2 = \(\frac{1}{2}\)mω2A2
At mean position y = 0, RE = 0, (KE)Max = – \(\frac{1}{2}\)mω2A2
∴ T.E = K.E + P.E
T.E = \(\frac{1}{2}\)mω2A2 + 0 = \(\frac{1}{2}\)mω2A2
At extreme position, y = A, K.E = 0 and,
(P.E)Max = \(\frac{1}{2}\)mω2A2.
∴ T.E = K.E + P.E
T.E. = O + \(\frac{1}{2}\)mω2A2 = \(\frac{1}{2}\)mω2A2
From mean position to extreme position K.E is to be converted into RE.
Problems
Question 1.
The bob of a pendulum is made of a hollow brass sphere. What happens to the time period of the pendulum, if the bob is filled with water completely ? Why?
Solution:
Time period (T) = \(2 \pi \sqrt{\frac{1}{g}}\)
The period of the pendulum is same. When the bob is hollow (or) completely filled with water. As water flows out from the bob, the centre of gravity of the bob lowers.
The pendulum length increases. Hence time period also increases. When the bob becomes empty, again centre of gravity shifts upwards. The pendulum length decreases. The time period also decreases.
![]()
Question 2.
Two identical springs of force constant “k” are joined one at the end of the other (in series). Find the effective force constant of the combination.
Solution:
k1 = k2 = k
If two springs are connected in series
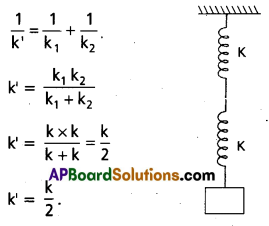
Question 3.
What are the physical quantities having maximum value at the mean position in SHM ?
Solution:
- Velocity, Vmax = Aω
- Kinetic energy, (K.E)Max = \(\frac{1}{2}\)mω2A2.
Question 4.
A particle executes SHM such that, the maximum velocity during the oscillation is numerically equal to half the maximum acceleration. What is the time period ?
Solution:
Given VMax = \(\frac{1}{2}\)aMax
Aω = \(\frac{1}{2}\)ω2
ω = 2
T = \(\frac{2 \pi}{\omega}\) = \(\frac{2 \pi}{2}\) = π sec.
Question 5.
A mass of 2 kg attached to a spring of force constant 260 Nm-1 makes 100 oscillations. What is the time taken ?
Solution:
m = 2 kg, k = 260 N/m
T = \(2 \pi \sqrt{\frac{m}{k}}\) = 2 × 3.14\(\sqrt{\frac{2}{260}}\) = 0.5508sec.
∴ Time for 100 oscillations = 100 × 0.5508
= 55.08 sec.
Question 6.
A simple pendulum in a stationery lift has time period T. What would be the effect on the time period when the lift
(i) moves up with uniform velocity
(ii) moves down with uniform velocity
(iii) moves up with uniform acceleration a
(iv) moves down with uniform acceleration ‘a’
(v) begins to fall freely under gravity ?
Solution:
i) When the lift moves up with uniform velocity
T = \(2 \pi \sqrt{\frac{1}{g}}\)
No change in time period.
ii) When the lift moves down with uniform velocity. No change in the time period.
iii) When the lift moves up with acceleration.
T = \(2 \pi \sqrt{\frac{1}{g+a}}\)
Time period decreases.
iv) When the lift moves down with acceleration.
T = 2π\(\sqrt{\frac{1}{g-a}}\)
Time period increases.
v) Lift falls freely, a = g
T = 2π\(\sqrt{\frac{l}{g-g}}\) = 2π\(\sqrt{\frac{1}{0}}\) = ∝
Time period becomes infinity.
Question 7.
A particle executing SHM has amplitude of 4 cm and its acceleration at a distance of 1 cm from the mean position is 3 cm s-2. What will is velocity be when it is at a distance of 2 cm from its mean position ?
Solution:
A = 4 cm, x1 = 1 cm, a = 3 cm/s2
a = ω2x1
3 = ω2 × 1
ω = \(\sqrt{3}\)
Velocity v = ω\(\sqrt{A^2-x_2^2}\)
(∵ x2 = 2 cm)
v = \(\sqrt{3} \sqrt{4^2-2^2}\)
v = \(\sqrt{3} \times \sqrt{12}\)
v = \(\sqrt{36}\) = 6 cm/s.
Question 8.
A simple harmonic oscillator has a time period of 2s. What will be the change in the phase 0.25 s after leaving the mean position ?
Solution:
T = 2 sec
t = 0.25 sec
sin ωt = sin\(\left(\frac{2 \pi}{T}\right) t\)
ϕ = ωt = \(\frac{2 \pi}{T}\) × t
= \(\frac{2 \pi}{2}\) × 0.25
ϕ = \(\frac{\pi}{4}\)
![]()
Question 9.
A body describes simple harmonic motion with an amplitude of 5 cm and a period of 0.2 s. find the acceleration and velocity of the body when the displacement is
(a) 5 cm.
(b) 3 cm.
(c) 0 cm.
Solution:
A = 5 cm = 5 × 10-2 m
T = 0.2 sec.
i) y = 5 cm = 5 × 10-2 m
ω = \(\frac{2 \pi}{T}\) = \(\frac{2 \pi}{0.2}\) = 10π
Acceleration (a) = -ω22y = -(10π)2 × 5 × 10-2
a = -5π2 m/s2
Velocity (v) = ω\(\sqrt{A^2-y^2}\)
= 10π\(\sqrt{\left(5 \times 10^{-2}\right)^2-\left(5 \times 10^{-2}\right)^2}\)
ii) y = 3 cm = 3 × 10-2 m
Acceleration (a) = -ω2y = -(10π)2 × 3 × 10-2
= -3π2 m/s2
Velocity (v) = ω\(\sqrt{A^2-y^2}\)
= 10π\(\sqrt{\left(5 \times 10^{-2}\right)^2-\left(3 \times 10^{-2}\right)^2}\)
= 10π\(\sqrt{25-9}\) × 10-2
v = 0.4π m/s.
iii) y = 0 cm
a = -ω2y = -(10π)2 × 0
Velocity (v) = ω\(\sqrt{A^2-y^2}\)
= 10π\(\sqrt{\left(5 \times 10^{-2}\right)^2-0}\)
= 0.5π m/s
Question 10.
The mass and radius of a planet are double that of the earth. If the time period of a simple pendulum on the earth is T, find the time period on the planet.
Solution:
g = \(\frac{\mathrm{GM}}{\mathrm{R}^2}\)
g ∝ \(\frac{M}{R^2}\)

Question 11.
Calculate the change in the length of a simple pendulum of length 1 m, when its period of oscillation changes from 2 s to 1.5 s. (T.S. Mar. ’18)
Solution:
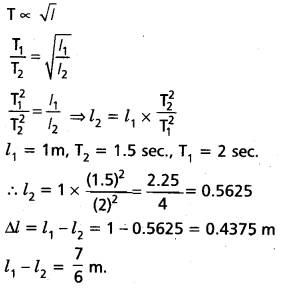
Question 12.
A freely falling body takes 2 seconds to reach the ground on a plane, when it is dropped from a height of 8 m. If the period of a simple pendulum is seconds on the planet, calculate the length of the pendulum.
Solution:
u = 0, t = 2 sec, s = h = 8 m
s = ut + \(\frac{1}{2}\)at
s = 0 × t + \(\frac{1}{2}\) × g × 22
g = 4m/s2
T = \(2 \pi \sqrt{\frac{1}{g}}\)
π = \(2 \pi \sqrt{\frac{1}{4}}\)
l = 1 m = 100 cm.
![]()
Question 13.
The period of a simple pendulum is found to increase by 50% when the length of the pendulum is increased by 0.6 m. Calculate the initial length and the initial period of oscillation at a place where g = 9.8 m s-2.
Solution:

Question 14.
A clock regulated by a second’s pendulum keeps correct time. During summer the length of the pendulum increases to 1.02 m. How much will the clock gain or lose in one day ?
Solution:
T = 2π\(\sqrt{\frac{1}{g}}\)
T ∝ \(\sqrt{l}\)
\(\frac{d T}{T}\) = \(\frac{1}{2} \frac{\mathrm{d} l}{l}\)
T = 2 sec, l = \(\frac{\mathrm{g}}{\pi^2}\) = 0.9927
dl = 1.02 – 0.9927 = 0.0273
\(\frac{d T}{2}\) = \(\frac{1}{2}\left(\frac{0.0273}{0.9927}\right)\)
dT = \(\frac{0.0273}{0.9927}\)
No. of oscillations performed per day by seconds pendulum = \(\frac{\text { One day }}{2 \text { Sec. }}\)
= \(\frac{86,400}{2}\) = 43,200.
The gain (or) loss of time per day = No. of oscillations in one day to the change in time for one oscillation = 43,200 × \(\frac{0.0273}{0.9927}\)
= 1180 sec.
Question 15.
The time period of a body suspended from a spring is T. What will be the new time period if the spring is cut into two equal parts and the mass is suspended
(i) from one part
(ii) simultaneously from both the parts ?
Answer:
T = \(2 \pi \sqrt{\frac{m}{k}}\)
i) Spring is cut into two parts, k’ = 2k
T’ = \(2 \pi \sqrt{\frac{m}{k^{\prime}}}\) = \(\frac{T}{\sqrt{2}}\)
ii) When the mass is suspended from both the parts
T = \(2 \pi \sqrt{\frac{m}{2 k+2 k}}\) = \(2 \pi \sqrt{\frac{m}{4 k}}\) = \(\frac{T}{2}\)
Additional Problems
Question 1.
Which of the following examples represent periodic motion ?
a) A swimmer completing one (return) trip from one bank of a river to the other and back. .
b) A freely suspended bar magnet displaced from its N – S direction and released.
c) A hydrogen molecule rotating about its centre of mass.
d) An arrow released from a bow.
Solution:
a) It is not a periodic motion. Though the motion of a swimmer is to and fro but will not have a definite period.
b) It is a periodic motion because a freely suspended magnet if once displaced from N-S direction and let it go, it oscillation about this position. Hence it is simple harmonic motion also.
c) It is also a periodic motion.
d) It is not a periodic motion.
Question 2.
Which of the following examples represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion ?
a) The rotation of earth about its axis.
b) Motion of an oscillating mercury column in a U-tube.
c) Motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lower most point.
d) General vibrations of a polyatomic molecule about its equilibrium position.
Solution:
a) It is periodic but not SHM because it is not to and fro motion about a fixed point.
b) It is SHM
c) It is SHM
d) It is a periodic but not SHM. A polyatomic gas molecule has a number of natural frequencies and its general motion is the resultant of S.H.M’s of a number of different frequencies. The resultant motion is periodic but not SHM.
![]()
Question 3.
Fig. depicts four x-t plots for linear motion of a particle. Which of the plots represent periodic motion ? What is the period of motion (in case of periodic motion)?
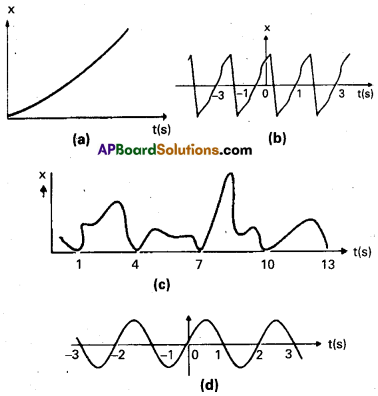
Solution:
a) Does not represent periodic motion, as the motion neither repeats nor comes to mean position.
b) Represents periodic motion with period equal to 2s.
c) Does not represent periodic motion, because it is not identically repeated.
d) Represents periodic motion with periodic equal to 2s.
Question 4.
Which of the following functions of time represent
(a) simple harmonic, (b) periodic but not simple harmonic, and (c) non-periodic motion ? Give period for each case of periodic motion (ω is any positive constant)
a) sin ωt – cos ωt
b) sin3 ωt
c) 3 cos (π/4 – 2ωt)
d) cos ωt + cos 3ωt + cos 5 ωt
e) exp (-ω2t2)
f) 1 + ωt + ω2t2.
Solution:
The function will represent a periodic motion, if it is identically repeated after a fixed interval of time and will represent SHM. If it can be written uniquely in the form of a
cos \(\left(\frac{2 \pi \mathrm{t}}{\mathrm{T}}+\phi\right)\) or a
sin \(\left(\frac{2 \pi \mathrm{t}}{\mathrm{T}}+\phi\right)\), where T is the time period.
a) sin ωt – cos ωt
= \(\sqrt{2}\)(\(\frac{1}{\sqrt{2}}\)sin ωt – \(\frac{1}{\sqrt{2}}\)cos ωt)
= \(\sqrt{2}\)(sin ωt cos \(\frac{\pi}{4}\) – cos ωt sin \(\frac{\pi}{4}\))
= \(\sqrt{2}\)(ωt\(\frac{\pi}{4}\))
It is a S.H.M and its period is 2π/ω.
b) sin3 ωt = \(\frac{1}{4}\)(3sin ωt – sin 3ωt)
Here each term sin ωt and sin 3ωt individually represents S.H.M. But (ii) which is the out come of the super position of two S.H.Ms will only be periodic but not S.H.M. its time period is 2π/ω.
(∵ cos (-θ) = cos θ).
c) 3 cos \(\left(\frac{\pi}{4}-2 \omega t\right)\) = 3 cos \(\left(2 \omega t-\frac{\pi}{4}\right)\)
Clearly it represents S.H.M. and its time period is 2π/2ω.
d) cos ωt + cos 3ωt + cos 5ωt it represents the periodic but not S.H.M its time period is 2π/ω.
e) \(\mathrm{e}^{-\omega^2 t^2}\) it is an exponential function which never repeats itself. Therefore it represents non-periodic motion.
f) 1 + ωt + ω2t2 also represents non periodic motion.
Question 5.
A particle is in linear simple harmonic motion between two points, A and B, 10 cm apart. Take the direction from A to B as the positive direction and give the signs of velocity, acceleration and force on the particle when it is
a) at the end A
b) at end B
c) at the mid-point of AB going towards A
d) at 2 cm away from B going towards A
e) at 3 cm away from A going towards B and
f) at 4 cm away from B going towards A.
Solution:
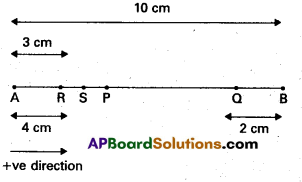
Refer figure here A and B represent the two extreme positions of a S.H.M. For velocity, the direction from A to B is taken as positive for acceleration and the force, the direction is taken positive if directed along AP and negative if directed along BP.
a) At the end A, the artice executing S.H.M is momentarily at rest being its extreme position of motion, hence its velocity is zero, acceleration is +ve because directed along AP. Force is also +ve since the force is directed towards AP i.e + ve direction.
b) At the end B, velocity is zero. Here acceleration and force are negative as they are directed along BP i.e. along negative direction.
c) At the mid point AB going towards A, the particle is at its mean position P, with a tendency to move along PA i.e. -ve direction. Hence velocity is -ve both acceleration and force are zero.
d) At 2 cm away from B going towards A, the particle is at Q, with a tendency to move along QP, which is a negative direction there velocity, acceleration and force are all -ve.
e) At 3 cm away from A going towards B, the particle is at R with a tendency to move along RP, which is positive direction, there, velocity, acceleration and force are all +ve.
f) At 4 cm away from A going towards A, the particle is at S, with a tendency to move along SA which is negative direction for velocity. Therefore velocity is negative but acceleration is directed towards mean position i.e., along SP, hence +ve. Similarly force is also +ve.
![]()
Question 6.
Which of the following relationships between the acceleration a and the displacement x of a particle involve simple harmonic motion ?
a) a = 0.7x
b) a = -200x2
c) a = -10x
d) a = 100x3
Solution:
In S.H.M acceleration a is related to displacement by the related of the form a = -kx which is for relation (c).
Question 7.
The motion of a particle executing simple harmonic motion is described by the displacement function.
x(t) = A cos (ωt + ϕ).
If the initial (t = 0) position of the particle is 1 cm and its initial velocity is ω cm/s, what are its amplitude and initial phase angle ? The angular frequency of the particle is πs-1. If instead of the cosine function, we choose the sine function to describe the SHM : x = B sin (ωt + α), what are the amplitude and initial phase of the particle with the above initial conditions.
Solution:
Here, at t = 0, x = 1 cm and v = ω cm s-1, ϕ = ?; ω = πs-1
Given x = A cos (ωt + ϕ)
1 = A cos (π × 0 + ϕ) or
= A cos ϕ —– (i)
Velocity, v = \(\frac{d x}{d t}\) = – Aω(sin ωt + ϕ)
∴ ω = -Aω sin (π × 0 + ϕ) or 1 = – A sin ϕ
or A sin ϕ = -1 —— (ii)
Squaring and adding (i) and (ii)
A2(cos2 ϕ + sin2 ϕ) = 1 + 1 = 2 or A2 = 2 or A = \(\sqrt{2}\) cm
Dividing (ii) by (i), we get
tan ϕ = -1 or ϕ = \(\frac{3 \pi}{4}\) or \(\frac{7 \pi}{4}\)
For, x = B sin (ωt + α) —— (iii)
At t = 0, x = 1, so,
1 = B sin (ω × 0 + α) = B sin α —– (iv)
Differentiating (iii), w.r.t, t we have dx
velocity, v = \(\frac{d x}{d t}\) = Bω cos (ωt + α)
Applying initial conditions i.e. at t = 0, v = ω
ω = Bωcos (π × 0 + α)
or 1 = B cos α —– (v)
Squaring and adding (iv) and (v) we get
B2sin2α + B2 cos2 α = 12 + 12 = 2 or B2 = 2 or B = \(\sqrt{2}\) cm
Dividing (iv) by (v), we have
\(\frac{B \sin \alpha}{B \cos \alpha}\) = \(\frac{1}{1}\) or tan α = 1 or α = \(\frac{\pi}{4}\) or \(\frac{5 \pi}{4}\).
Question 8.
A spring balance has a scale that reads from 0 to 50 kg. The length of the scale is 20 cm. A body suspended from this balance, when displaced and released, oscillates with a period of 0.6 s. What is the weight of the body ?
Solution:
Here. m = 50 kg, max. extension.
y = 20 – 0 = 20 cm = 0.2 m; T = 0.65
Max. Force, F = mg = 5 × 9.8 N
K = \(\frac{F}{y}\) = \(\frac{50 \times 9.8}{0.2}\) = 2450 Nm-1
As T = \(2 \pi \sqrt{\frac{m}{k}}\)
m = \(\frac{T^2 k}{4 \pi^2}\)
= \(\frac{(0.6)^2 \times 2450}{4 \times(3.14)^2}\)
= 22.36 kg
∴ Weight of body = mg = 22.36 × 9.8
= 219.1 N
= 22.36 kgf
![]()
Question 9.
A spring having with a spring constant 1200 Nm-1 is mounted on a horizontal table as shown in fig. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.
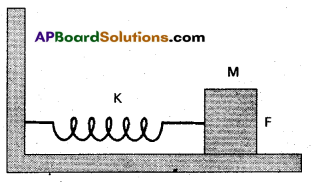
Determine
(i) the frequency of oscillations,
(ii) maximum acceleration of the mass, and
(iii) the maximum speed of the mass.
Solution:
Here, k = 1200 Nm-1, m = 3.0 kg, a = 2.0 cm = 0.02 m
a)
Frequency,
υ = \(\frac{1}{T}\) = \(\frac{1}{2 \pi} \sqrt{\frac{k}{m}}\)
= \(\frac{1}{2 \times 3.14} \sqrt{\frac{1200}{3}}\)
= 3.2s-1
b) Acceleration A = ω2y = \(\frac{k}{m}\)y
Acceleration will be maximum when y is maximum i.e. y = a
Max. acceleration, Amax = \(\frac{k_a}{m}\) = \(\frac{1200 \times 0.02}{3}\)
= 8 ms-2
c) Max. speed of the mass will be when it is passing through the mean position, which is given by
Vmax = aω = a\(\sqrt{\frac{k}{m}}\)
= 0.02 × \(\sqrt{\frac{1200}{3}}\) = 0.4 ms-1
Question 10.
In exercise, let us take the position of mass when the spring is unstreched as x = 0, and the direction from left to right as the positive direction of x-axis. Give x as a function of time t for the oscillating mass if at the moment we start the stopwatch (t = 0), the mass is
a) at the mean position
b) at the maximum stretched position and
c) at the maximum compressed position
In what way do these functions for SHM differ from each other, in frequency, in amplitude or the initial phase ?
Solution:
Here, a = 2.0 cm; ω = \(\sqrt{\frac{k}{m}}\) = \(\sqrt{\frac{1200}{3}}\) = 20s-1
a) As time is noted from the mean position, hence using
x = a sin ωt, we have x = 2 sin 20t
b) At maximum stretched position, the body is the extreme right position, with an initial phase of \(\frac{\pi}{2}\) rad. Then
x = a sin \(\left(\omega t+\frac{\pi}{2}\right)\)
= a cos ωt = 2 cos 20t
c) At maximum compressed position, the body is at the extreme left position, with an initial phase of \(\frac{3 \pi}{2}\) rad.
Then x = a sin (ωt + \(\frac{3 \pi}{2}\))
= -a cos ωt
= -2 cos 20t
Question 11.
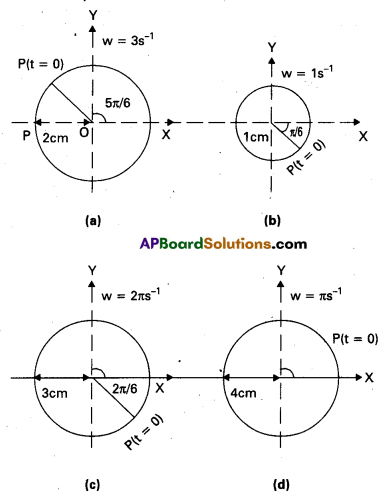
Figures correspond to two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution (i.e. clockwise or anti-clockwise) are indicated on each figure.
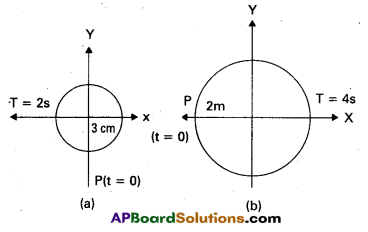
Obtain the corresponding simple ‘ harmonic motions of the x-projection of the radius vector of the revolving particle P, in each case.
Solution:
In Fig. (a) T = 2s ; a = 3 cm
At t = 0, OP makes an angle \(\frac{\pi}{2}\) with X-axis
i.e., ϕ = \(\frac{\pi}{2}\) radian.
While moving clockwise, here ϕ = +\(\frac{\pi}{2}\). Thus the X-projection of OP at time t will give us the equation of S.H.M. given by
x = a cos \(\left(\frac{2 \pi t}{T}+\phi\right)\)
= 3cos \(\left(\frac{2 \pi t}{2}+\frac{\pi}{2}\right)\) or x = -3
sin πt (x is in cm)
In Fig. (b) T = 4s ; a = 2m
At t = 0, OP makes an angle π with the positive direction of X-axis i.e., ϕ = π. While moving anticlockwise, here ϕ = +π.
Thus the X-projection of OP at time t will give us the equation of S.H.M. as
x = a cos \(\left(\frac{2 \pi t}{T}+\phi\right)\)
= 2 cos \(\left(\frac{2 \pi t}{4}+\pi\right)\)
= -2 cos \(\left(\frac{\pi}{2} t\right)\) (x is in m)
Question 12.
Plot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial (t = 0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case : (x is in cm and t is in s).
a) x = -2 sin (3t + π/3)
b) x = cos (π/6 – t)
c) x = 3 sin (2πt + π/4)
d) x = 2 cos πt.
Solution:
If we express each function of the form
x = a cos (cot + ϕ) —— (i)
Where ϕ is the initial phase i.e., ϕ represents the angle which the initial radius vector of the particle makes with the -l-ve direction of X-axis.
a) x = -2 sin (3t + \(\frac{\pi}{3}\)) = 2 cos (\(\frac{\pi}{2}\) + 3t + \(\frac{\pi}{3}\))
or x = 2 cos (3t + \(\frac{5 \pi}{6}\))
Comparing it with equation (i), we note
that a = 2, ω = 3 and ϕ = \(\frac{5 \pi}{6}\)
Hence, the reference circle will be shown in Fig. (a).
b) x = cos\(\left(\frac{\pi}{6}-t\right)\) = cos \(\left(t-\frac{\pi}{6}\right)\)
(∵ cos (-θ) = cos θ))
Comparing it with equation (i), we note
that a = 1, ω and ϕ = \(\frac{\pi}{6}\)
The reference circle will be as shown in Fig. (b).
c) x = 3 sin \(\left(2 \pi t+\frac{\pi}{4}\right)\)
= 3 cos \(\left(2 \pi t+\frac{3 \pi}{2}+\frac{\pi}{4}\right)\)
Comparing it with equation (i), we note that a = 3, ω = 2π and ϕ = \(\frac{3 \pi}{2}\) + \(\frac{\pi}{4}\) = \(\frac{7 \pi}{4}\)
The reference circle will be as in Fig. (c).
d) x = 2 cos πt
Comparing it with equation (i), we note
that a = 2, = π and ϕ = 0.
The reference circle will be as shown Fig. (d)
![]()
Question 13.
Figures (a) shows a spring of force constant k clamped rigidly at one end and a mass m attached to its free end. A force F applied at the free end stretches the spring. Figure (b) shows the same spring with both ends free and attached to a mass at either end. Each end of the spring in Fig. (b) is stretched by the same force F.
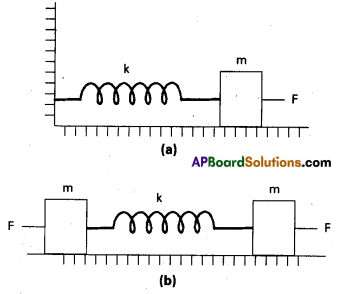
a) What is the maximum extension of the spring in two cases ?
b) If the mass in Fig. (a) and the two masses in Fig. (b) are released, what is the period of oscillation in each case ?
Solution:
a) The maximum extension of the spring in both the cases will be = \(\frac{F}{K}\), where K is the spring constant of the spring used.
b) In Fig. (a), if x is the extension in the spring, when mass m is returning to its mean posi-tion after being released free, then restoring force on the mass is F = -Kx i.e., F ∝ x.
As this F is directed towards mean position of the mass, hence the mass attached to the spring will execute SHM. Here, spring factor = spring constant
= K
Inertia factor = mass of the given mass
= m
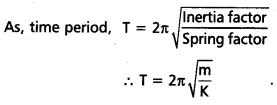
In Fig.(b). we have a two body system of spring constant K and reduced mass,
μ = \(\frac{m \times m}{m+m}\) = \(\frac{m}{2}\)
Here, inertia factor = \(\frac{m}{2}\)
and spring factor = K
∴ Time period, T = 2π\(\sqrt{\frac{(m / 2)}{k}}\)
= 2π\(\sqrt{\frac{m}{2 K}}\)
Question 14.
The piston in the cylinder head of a locomotive has a stroke (twice the amplitude) of 1.0 m. If the piston moves with simple harmonic motion with an angular frequency of 200 rad/min. what is its maximum speed ?
Solution:
Given a = \(\frac{1}{2}\)m; ω = 200 rev/min ;
Vmax = aω
= \(\frac{1}{2}\) × 200
= 100 m/min.
Question 15.
The acceleration due to gravity on the surface of moon is 1.7 ms-2. What is the time period of a simple pendulum on the surface of moon if its time period on the surface of earth is 3.5 s ? (g on the surface of earth is 9.8 ms-2).
Solution:
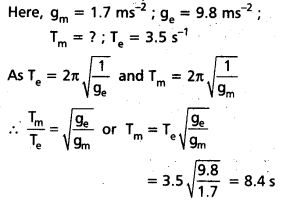
Question 16.
Answer the following questions :
a) Time period of a particle in SHM depends on the force constant k and mass m of the particle :
T = \(2 \pi \sqrt{\frac{\mathrm{m}}{\mathrm{k}}}\). A simple pendulum executes SHM approximately. Why then is the time period of a pendulum independent of the mass of the pendulum ?
b) The motion of a simple pendulum is approximately simple harmonic for small angle oscillations. For larger angles of oscillation, a more involved analysis shows that T is greater than \(2 \pi \sqrt{\frac{l}{g}}\). Think of a qualitative argument to appreciate this result.
c) A man with a wristwatch on his hand falls from the top of a tower. Does the watch give correct time during the free fall ?
d) What is the frequency of oscillation of a simple pendulum mounted in cabin that is freely falling under gravity ?
Solution:
a) For a simple pendulum, force constant or spring factor K is proportional to mass m, therefore, m cancels out in denominator as well as in numerator. That is why the time period of simple pendulum is independent of the mass of the bob.
b) The effective restoring force acting on the bob of simple pendulum in displaced position is
F = -mg sin θ. When θ is small, sin θ = θ. Then the expression for time period of simple pendulum is given by T = \(2 \pi \sqrt{\mu \mathrm{g}}\) When θ is large sin θ < θ, if the restoring force mg sin θ is replaced by mgθ, this amounts to effective reduction in the value of ‘g’ for large angles and hence an increase in the value of time period T.
c) Yes, because the working of the wrist watch depends on spring action and it has nothing to do with gravity.
d) We know that gravity disappears for a man under free fall, so frequency is zero.
Question 17.
A simple pendulum of length l and having a bob of mass M is suspended in a car. The car is moving on a circular track of radius R with a uniform speed v. If the pendulum makes small oscillations in a radial direction about its equilibrium position, what will be its time period ?
Solution:
Centripetal acceleration, ac = \(\frac{v^2}{R}\), it is acting horizontally.
Acceleration due to gravity = g acting vertically downwards.
Effective acceleration due to gravity
g’ = \(\sqrt{g^2+\frac{v^4}{R^2}}\)
∴ Time period, T = 2π\(\sqrt{\frac{1}{g}}\)
= 2π\(\sqrt{\frac{1}{g^2+v^4 / R^2}}\)
![]()
Question 18.
A cylindrical piece of cork of density of base area A and height h floats in a liquid of density ρ1. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period.
T = \(2 \pi \sqrt{\frac{h \rho}{\rho_1 g}}\)
where ρ is the density of cork. (Ignore damping due to viscosity of the liquid).
Solution:
Mass of the cylinder (m) = volume × density
= Ahρ ——- (1)
F1 = weight of the liquid displaced by the length l of the cylinder
= (Al)ρ1g —— (2)
Weight of the cylinder = mg —– (3)
In equilibrium position, mg = Alρ1g
m = Alρ1 —– (4)
F2 = A(l + y)ρ1g —– (5)
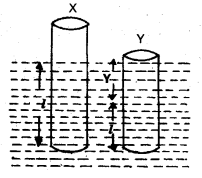
Restoring force (F) = -(F2 – mg)
= -[A(l + y)ρ1g – Alρ1g]
F = Ayρ1g = -(Aρ1g)y —— (6)
In S.H.M. F = -Ky —– (7)
From eqs. (6) & (7),
spring factor (K) = Aρ1g ——(8)
Inertia factor, m = Ahρ ——- (9)
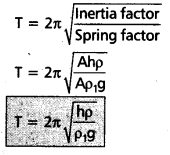
Question 19.
One end of a U-tube containing mercury is connected to a suction pump and the other end to atmosphere. A small pressure difference is maintained between the two columns. Show that, when the suction pump is removed, the column of mercury in the U-tube executes simple harmonic motion.
Solution:
Consider a liquid of density ρ contained in a vertical U-tube of cross-sectional area A. Total length of the liquid column from P to P1 is L.
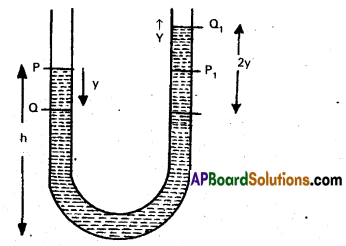
Mass (m) = LAρ
PQ = y, P1Q1 = y, QQ1 = 2y
Restoring force (F) = -(A2y)ρg
= -(2Aρg)y —– (1)
F ∝ -y
Hence oscillations in U-tube is S.H.M.
Question 20.
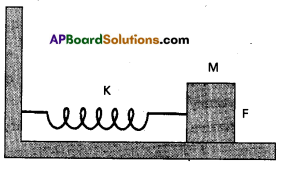
An air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.). Show that when the ball is pressed down a little and released, it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal (see Fig.).

Solution:
Consider an air chamber of volume V with a long neck of uniform area of cross-section A, and a frictionless ball of mass m filled smoothly in the neck at position C. The pressure of air below the ball inside the chamber is equal to the atmospheric pressure. Increase the pressure on the ball by a little amount P, so that the ball is depressed to position D, where CD = y.
There will be decrease in volume and hence increases in pressure of air inside the chamber. The decrease in volume of the air inside the chamber.

Here, negative sign shows that the increase in pressure will decrease the volume of air in the chamber.
Now, ρ = \(\frac{-E A y}{V}\)
Due to this excess pressure, the restoring force acting on the ball is
F = P × A = \(\frac{-E A y}{V} \cdot A\)
= \(\frac{-E A^2}{V} y\) —- (1)
Since F ∝ y and negative sign shows that the force is directed towards equilibrium position, if the applied increased pressure is removed from the ball, the ball with start executing linear SHM in the neck of chamber with C as mean position.
In a S.H.M., the restoring force,
F = -Ky —- (2)
Comparing (1) and (2), we have spring factor.
K = \(\frac{E A^2}{V}\)
Here, inertia factor = mass of ball = m
Inertia factor Spring factor

Note : If the ball oscillates in the neck of chamber under isothermal conditions, then E = P = Pressure of air inside the chamber, when ball is at equilibrium position. If the ball oscillates in the neck of chamber under adiabatic conditions, then E = υP, where v = \(\frac{c_p}{c_v}\).
Question 21.
You are riding in an automobile of mass 3000 kg. Assuming that you are examining the oscillation characteristics of its suspension system. The suspension sags 15 cm when the entire automobile is placed on it. Also, the amplitude of oscillation decreases by 50% during one complete oscillation. Estimate the values of (a) the spring constant k and (b) the damping constant b for the spring and shock absorber system of one wheel, assuming that each wheel supports 750 kg.
Solution:
Here, M = 3000 kg ; x = 0.15 cm ; if K is the spring constant of each spring, then spring constant of 4 springs in parallel to support the whole mass is, K = 4 K.
4 kx = Mg
k = \(\frac{M g}{4 x}\)
= \(\frac{3000 \times 10}{4 \times 0.15}\)
= 5 × 104 N/m.
b) If m is the mass supported by each spring, then m = \(\frac{3000}{4}\) = 750 kg.

Question 22.
Show that for a particle in linear SHM the average kinetic energy over a period of oscillation equals the average potential energy over the same period.
Solution:
Consider a particle of mass m be executing S.H.M. with period T. The displacement of the particle at an instant t, when time period is noted from the mean position is given by
Y = a sin ωt
∴ Velocity 1 V = \(\frac{\mathrm{dy}}{\mathrm{d} \mathrm{t}}\) = aω cos ωt
K.E., EK = \(\frac{1}{2}\)mv2 = \(\frac{1}{2}\)ma2ω2 cos2 ωt
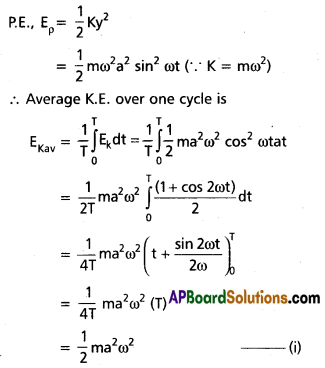
Average P.E. over one cycle is
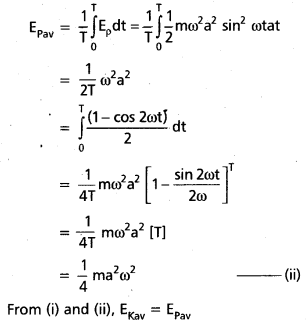
![]()
Question 23.
A circular disc of mass 10 kg is suspended by a wire attached to is centre. The wire is twisted by rotating the disc and released. The period of torsional oscillations is found to be 1.5s. The radius of the disc is 15 cm. Determine the torsional spring constant of the wire. (Torsional spring constant a is defined by the relation J = -α θ, where J is the restoring couple and θ the angle of twist).
Solution:
Here, m = 10kg; R = 15 cm = 0.15m; T = 1.55, ∝ = ?
Moment of inertia of disc,
I = \(\frac{1}{2} m R^2\)
= \(\frac{1}{2}\) × 10 × (0.15)2 kgm2
Now T = \(2 \pi \sqrt{\frac{1}{\alpha}}\)
so, α = \(\frac{4 \pi^2 1}{T^2}\)
= 4 × \(\left(\frac{22}{7}\right)^2\) × \(\frac{1}{2}\) × \(\frac{10 \times(0.15)^2}{(1.5)^2}\)
= 1.97Nm/rad.
Question 24.
A body describes simple harmonic motion with an amplitude of 5 cm and a period of 0.2 s. Find the acceleration and velocity of the body when the displacement is
(a) 5 cm
(b) 3 cm
(c) 0 cm.
Solution:
Here, r = 5 cm = 0.05 m ; T = 0.25 ;
ω = \(\frac{2 \pi}{\mathrm{T}}\) = \(\frac{2 \pi}{0.2}\)
= 10p rad/s
When displacement is y, then acceleration
A = -ω2y
Velocity, v = ω\(\sqrt{r^2-y^2}\)
Case (a) : When y = x cm = 0.05 m
A = -(10π)2 × 0.05
= -5π2 m/s2
V = 10π\(\sqrt{(0.05)^2-(0.05)^2}\) = 0
Case (b) : When y = 3 cm = 0.03 m
A = -(10π)2 × 0.03
= -3π2 m/s2
V= 10π × \(\sqrt{(0.05)^2-(0.03)^2}\)
= 10π × 0.04
= 0.4π m/s
Case (c): When y = 0,
A = -(10π)2 × 0 = 0
V= 10π\(\sqrt{(0.05)^2-(0)^2}\)
= 10π × 0.05
= 0.5π m/s.
Question 25.
A mass attached to a spring is free to oscillate, with angular velocity ω, in a horizontal plane without friction or damping. It is pulled to a distance x0 and pushed towards the centre with a velocity v0 at time t = 0. Determine the amplitude of the resulting oscillations in terms of the parameters ω, x0 and V0.
[Hint : Start with the equation x = a cos (ωt + θ) and note that the initial velocity is negative.]
Solution:
x = A cos (ωt + θ) dx
Velocity, \(\frac{\mathrm{dx}}{\mathrm{dt}}\) = -Aω sin (ωt + θ) dt
When t = 0, x = x0, and \(\frac{\mathrm{dx}}{\mathrm{dt}}\) = -V0
∴ x0 = A cos θ
-V0 = -Aω sin θ or A sin θ = \(\frac{V_0}{\omega}\)
Squaring and adding- (i) and (ii), we get
A2(sin2 θ + cos2 θ) = \(\left(\frac{v_0^2}{\omega^2}\right)+x_0^2\)
A = \(\left[\frac{v_0^2}{\omega^2}+x_0^2\right]^{1 / 2}\)