AP Inter 1st Year Physics Study Material Chapter 9 గురుత్వాకర్షణ

Andhra Pradesh BIEAP AP Inter 1st Year Physics Study Material 9th Lesson గురుత్వాకర్షణ Textbook Questions and Answers.

AP Inter 1st Year Physics Study Material 9th Lesson గురుత్వాకర్షణ

అతిస్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
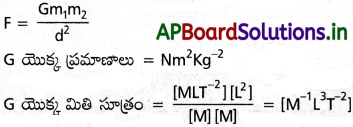
విశ్వ గురుత్వ స్థిరాంకం (G) ప్రమాణాలను, మితులను తెలపండి.
జవాబు:

ప్రశ్న 2.
నూటన్ గురుత్వాకర్షణ నియమాన్ని సదిశా రూపంలో వ్యక్తీకరించండి.
జవాబు:
న్యూటన్ గురుత్వాకర్షణ నియమం యొక్క సదిశా రూపం
F = \(\frac{-G m_1 m_2}{r^3} \hat{r}\) ఇక్కడ \(\hat{r}\) అనునది ఏకాంక సదిశ.

ప్రశ్న 3.
చంద్రునిపై భూమి గురుత్వాకర్షణ బలం F అయితే, భూమిపై చంద్రుని గురుత్వాకర్షణ బలం ఎంత? ఈ బలాలు చర్య-ప్రతిచర్య జంటను ఏర్పరుస్తాయా?
జవాబు:
F. అవును. ఈ బలాలు చర్య-ప్రతిచర్యల జంటను ఏర్పరుస్తాయి.

ప్రశ్న 4.
భూమి ద్రవ్యరాశిని స్థిరంగా ఉంచుతూనే, భూమి వ్యాసార్థం 2% తగ్గిస్తే, దాని ఉపరితలం వద్ద గురుత్వ త్వరణం విలువ (g)లో వచ్చే మార్పు ఎంత ఉంటుంది?
జవాబు:

ప్రశ్న 5.
మనం ఒక గ్రహం నుంచి మరొక గ్రహానికి మారుతూ ఉంటే వస్తువు a) ద్రవ్యరాశి b) భారం ఎలా మారుతుంటాయి?
జవాబు:
a) ద్రవ్యరాశి మారదు.
b) ఒక గ్రహం నుండి వేరొక గ్రహానికి మారితే భారం (w = mg) కూడా మారుతుంది.

ప్రశ్న 6.
ఒక లఘులోలకం పొడవును స్థిరంగా ఉంచినప్పుడు, అన్ని గ్రహాల మీద దాని డోలనావర్తన కాలం సమానంగా ఉంటుందా? కారణంతో సహా మీ సమాధానాన్ని సమర్థించండి.
జవాబు:
ఉండదు. ఆవర్తన కాలం, గురుత్వ త్వరణంపై ఆధారపడుతుంది. T = 2π\(\sqrt{\frac{l}{g}}\) విలువ ఒక్కో గ్రహానికి ఒక్కో విధంగా ఉంటుంది. కావున ఆవర్తన కాలం మారుతుంది.

ప్రశ్న 7.
భూఉపరితలం నుంచి d లోతులో ఉన్న బిందువు వద్ద గురుత్వ త్వరణానికి సమీకరణాన్ని తెలపండి. భూకేంద్రం వద్ద g విలువ ఎంత?
జవాబు:

1. g_d = g(1- \(\frac{d}{R}\)) ఇక్కడ d = లోతు, R = వ్యాసార్ధం.
2. భూకేంద్రం వద్ద g = 0.

ప్రశ్న 8.
g విలువను భూమధ్యరేఖ వద్ద కనిష్ఠంగా, ధ్రువాల వద్ద గరిష్ఠంగా ఉండే విధంగా చేసే అంశాలేమిటో తెలపండి.
జవాబు:

1. g విలువ ధ్రువాల వద్ద అధికంగా ఉండుటకు కారణం (a) భూభ్రమణం వల్ల (b) ధ్రువాల వద్ద భూమి చదునుగా ఉండటం (c) ధ్రువాల వద్ద లంబ వ్యాసార్థం తక్కువగా ఉండటం.
2. భూమధ్యరేఖ వద్ద g విలువ తక్కువగా ఉండుటకు కారణం (a) భూభ్రమణం వల్ల (b) భూమధ్యరేఖ వద్ద ఉబ్బెత్తుగా ఉండటం.

ప్రశ్న 9.
“హైడ్రోజన్ సూర్యుని చుట్టూ పుష్కలంగా ఉంది. కాని భూమి చుట్టూ అంత పుష్కలంగా లేదు”. వివరించండి.
జవాబు:
సూర్యుడిపై పలాయన వేగం 620 km/s మరియు భూమిపై పలాయన వేగం 11.2 km/s హైడ్రోజన్ వాయువు పలాయన వేగం (2 km/s), సూర్యుడిపై పలాయన వేగం కన్నా బాగా తక్కువ. అందువలన హైడ్రోజన్ సూర్యుడి చుట్టూ పుష్కలంగాను, భూమి చుట్టూ పలుచగాను ఉంటుంది.

ప్రశ్న 10.
ఒక భూస్థావర ఉపగ్రహం పరిభ్రమణావర్తన కాలం ఎంత? అది పశ్చిమం నుంచి తూర్పుకి లేదా తూర్పు నుంచి పశ్చిమానికి తిరుగుతుందా?
జవాబు:
భూస్థావర ఉపగ్రహం యొక్క ఆవర్తన కాలం 24 గంటలు. ఇది పశ్చిమం నుంచి తూర్పు వైపుకు తిరుగుతుంది.

ప్రశ్న 11.
ధ్రువీయ ఉపగ్రహాలు అంటే ఏమిటి?
జవాబు:
తక్కువ ఎత్తులో (500 నుండి 800 km) తిరిగే ఉపగ్రహాలను ధ్రువీయ ఉపగ్రహాలు అంటారు. ఇవి భూమి యొక్క ధ్రువాల చుట్టూ ఉత్తరం నుండి దక్షిణ దిశలో తిరుగుతాయి. వీటి ఆవర్తన కాలం దాదాపు 100 నిముషాలు.

స్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
కెప్లర్ గ్రహ గమన నియమాలను పేర్కొనండి.
జవాబు:
కెప్లర్ యొక్క మూడు నియమాలను ఈ విధంగా తెలపవచ్చు.

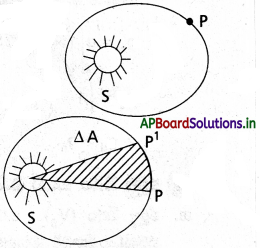
1. కక్ష్యల నియమం :
సూర్యుడిని కేంద్రంగా చేసుకొని అన్ని గ్రహాలు సూర్యుని చుట్టూ దీర్ఘవృత్తాకార కక్ష్యలో తిరుగుతాయి.

2. వైశాల్యాల నియమం :
గ్రహం నుండి సూర్యుడిని కలిపే రేఖ సమాన కాలవ్యవధులలో సమాన వైశాల్యాలను చిమ్ముతుంది.

3. ఆవర్తన కాలాల నియమం :
గ్రహం యొక్క పరిభ్రమణ ఆవర్తన కాల వర్గము, ఆ గ్రహ దీర్ఘవృత్తాకార కక్ష్య అర్థగురు అక్షం పొడవు ఘనానికి అనులోమాను పాతంలో ఉండును.
T² α R³

ప్రశ్న 2.
ఒక గ్రహం ఉపరితలంపై గురుత్వ త్వరణం విలువ (g), విశ్వ గురుత్వ స్థిరాంకం (G)ల మధ్య సంబంధాన్ని రాబట్టండి.
జవాబు:
m ద్రవ్యరాశి గల వస్తువు గ్రహం యొక్క ఉపరితలంపై ఉంది అనుకొనుము.
భూమి వ్యాసార్థం R మరియు భూమి ద్రవ్యరాశి M అనుకొనుము.
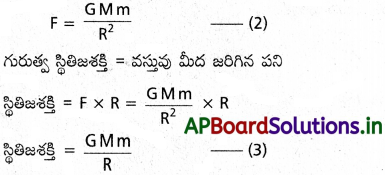
వస్తువు గ్రహం యొక్క గురుత్వాకర్షణ బలం (F) = mg ………… (1)

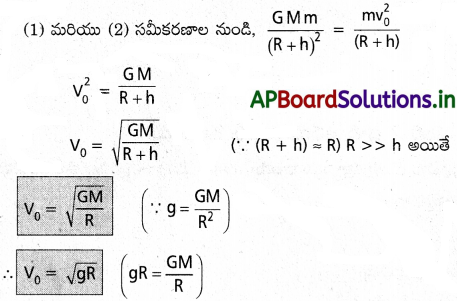
న్యూటన్ గురుత్వాకర్షణ నియమం ప్రకారం, వస్తువుపై బలం
F = \(\frac{GMm}{R^2}\) …………… (2)
(1) మరియు (2) సమీకరణాల నుండి mg = \(\frac{GMm}{R^2}\)
g = \(\frac{GM}{R^2}\) ఇది g మరియు Gల మధ్య సంబంధం.
భూమి ద్రవ్యరాశి (M) = ఘనపరిమాణం × భూమి యొక్క సాంద్రత
M = \(\frac{4}{3}\) πR³ × ρ
g = \(\frac{4}{3}\) πGRρ

ప్రశ్న 3.
సమాన విలువలు కలిగిన ఎత్తు (h), లోతు (d)లకు గురుత్వ త్వరణం విలువ ఏ విధంగా మారుతుంది?
జవాబు:

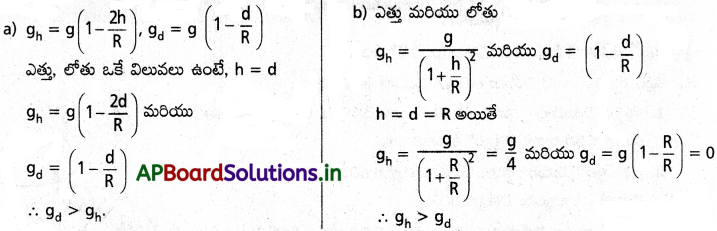
ప్రశ్న 4.
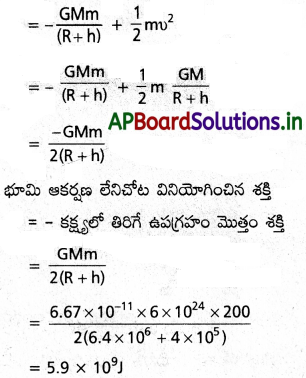
కక్ష్యా వేగం అంటే ఏమిటి? దానికి సమీకరణాన్ని ఉత్పాదించండి. [Mar. 14]
జవాబు:

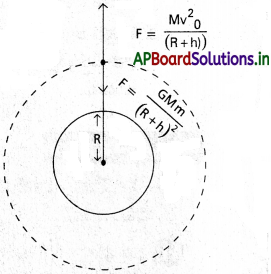
కక్ష్యా వేగం (V) :
ఒక గ్రహం చుట్టూ నిర్ణీత కక్ష్యలో వృత్తాకార మార్గంలో పరిభ్రమించడానికి వస్తువుకు కావలసిన కనీస క్షితిజ సమాంతర వేగాన్ని కక్ష్యావేగం అంటారు.

కక్ష్యా వేగానికి సమీకరణంను రాబట్టుట :
భూమి చుట్టూ m ద్రవ్యరాశి గల వస్తువు (ఉపగ్రహం) వృత్తాకారంగా పరిభ్రమిస్తున్నది అనుకొనుము. భూమి నుండి ఉపగ్రహం ఎత్తు అనుకొనుము. అపుడు కక్ష్యా వ్యాసార్థం . (R + b) అవుతుంది.

వస్తువుపై భూమి కలిగించే గురుత్వాకర్షణ బలం (F) = \(\frac{GMm}{(R+h)^2}\) ………. (1)
ఇక్కడ M = భూమి ద్రవ్యరాశి, R = భూమి యొక్క వ్యాసార్థం,
G = విశ్వగురుత్వ స్థిరాంకం, V_o అనునది వస్తువు యొక్క కక్ష్యా వేగం అయితే

వస్తువుపై పనిచేసే అపకేంద్ర బలం (F) = \(\frac{mv^2_0}{(R+h)^2}\) ………. (2)

వస్తువు సమవడితో వృత్తాకార కక్ష్యలో తిరగడానికి అవసరమయ్యే అపకేంద్ర బలాన్ని, వస్తువుపై గ్రహం కలుగచేసే గురుత్వాకర్షణ బలం అందించును.

ప్రశ్న 5.
పలాయన వడి అంటే ఏమిటి? దానికి సమీకరణాన్ని ఉత్పాదించండి. [Mar. ’13]
జవాబు:
పలాయన వేగం :
ఒక వస్తువును భూమి గురుత్వాకర్షణను అధిగమించి తప్పించుకుపోవడానికి, ఎంత కనీసవేగంతో ప్రక్షిప్తం చేయాలో ఆ వేగాన్ని పలాయన వేగం అంటారు.

పలాయన వేగానికి సమీకరణం :
m ద్రవ్యరాశి గల వస్తువును v_e వేగంతో విసిరామనుకొనుము.
గతిజశక్తి = \(\frac{1}{2}\)mv²_e ………….. (1)
భూమి ద్రవ్యరాశి M, వ్యాసార్థం R అయిన m ద్రవ్యరాశి గల వస్తువుపై గురుత్వాకర్షణ బలం

గతిజశక్తి = స్థితిజశక్తి అయితే వస్తువు పలాయనం చేస్తుంది.

∴ పలాయన వేగం, కక్ష్యావేగానికి √2 రెట్లుండును.

ప్రశ్న 6.
భూస్థావర ఉపగ్రహం అంటే ఏమిటి? వాటి ఉపయోగాలను తెలపండి. [May ’13]
జవాబు:
భూస్థావర ఉపగ్రహం :
కృత్రిమ ఉపగ్రహం యొక్క కక్ష్యావర్తన కాలము, భూమి యొక్క ఆత్మభ్రమణ కాలానికి సమానమైతే అటువంటి ఉపగ్రహాన్ని భూస్థావర ఉపగ్రహం అంటారు.

ఉపయోగాలు :

1. వాతావరణ పైపొరలను అధ్యయనం చేయవచ్చు.
2. వాతావరణంలో కలిగే మార్పులను తెలుసుకోవచ్చును.
3. భూమి ఆకారాన్ని, పరిమాణాన్ని అంచనా వేయవచ్చును.
4. భూఉపరితలంపై, భూగర్భంలోను గల సహజ ఖనిజ సంపదను గుర్తించవచ్చును.
5. టెలివిజన్ కార్యక్రమాలను సుదూర ప్రాంతాలకు ప్రసారం చేయవచ్చును.
6. అంతరిక్ష పరిశోధన చేసి గ్రహాలు, ఉపగ్రహాలు, తోకచుక్కలు మొదలగు వాటి గూర్చి పరిశోధించవచ్చు.

ప్రశ్న 7.
సరాసరి సముద్ర మట్టం నుంచి రెండు ప్రదేశాలు ఒకే ఎత్తులో ఉన్నాయనుకొందాం. ఒకటి పర్వతం మీద ఉంది. మరొకటి గాలిలో ఉంది. ఎక్కడ ‘g’ ఎక్కువగా ఉంటుంది? మీ సమాధానానికి కారణం తెలపండి.
జవాబు:
గాలిలో కన్నా పర్వతం మీద గురుత్వ త్వరణం విలువ ఎక్కువ.
g = \(\frac{GM}{(R+h)^2}\) ………. (1)
ద్రవ్యరాశి (M) = ఘనపరిమాణం × సాంద్రత (ρ)
M = \(\frac{4}{3}\)πR³ × ρ

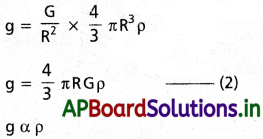
కాబట్టి పర్వతం సాంద్రత ఎక్కువ కాబట్టి పర్వతం మీద g విలువ ఎక్కువ.

ప్రశ్న 8.
ఒక వస్తువు భారం భూమధ్యరేఖ వద్ద కంటే ధ్రువాల వద్ద ఎక్కువగా ఉంటుంది. ఒకే బరువుకు ఈ రెండు ప్రదేశాల్లో ఎక్కడ ఎక్కువ చక్కెర (sugar) వస్తుంది? మీ సమాధానానికి కారణం తెలపండి.
జవాబు:
ధ్రువాల వద్ద వస్తువు యొక్క భారం = m_pg_p (∵ w = mg)
భూమధ్యరేఖ వద్ద వస్తువు యొక్క భారం = m_eg_e
ధ్రువాల వద్ద వస్తువు యొక్క భారం > భూమధ్యరేఖ వద్ద వస్తువు యొక్క భారం
m_p g_p > m_e g_e
g_p > g_e అని మనకు తెలుసు కాబట్టి m_p < m_e
అందువలన భూమధ్యరేఖ వద్ద మనం ఎక్కువ చక్కెరను పొందగలం.

ప్రశ్న 9.
భూమి చుట్టూ తిరుగుతున్న ఒక కృత్రిమ ఉపగ్రహం చీల (nut) వదులై దాని నుంచి వేరయిపోతే అది భూమి వైపు కిందకు పడుతుందా? లేదా భూమి చుట్టూ తిరుగుతుందా? మీ సమాధానానికి కారణం తెలపండి.
జవాబు:
కృత్రిమ ఉపగ్రహం నుండి ఒక చీల క్రిందపడితే, అది ఉపగ్రహం యొక్క వేగంతోనే చలించడం ప్రారంభిస్తుంది. ఉపగ్రహం యొక్క కక్ష్యా వేగం దాని ద్రవ్యరాశిపై ఆధారపడదు. అభికేంద్ర బలం వల్ల చీల కూడా ఉపగ్రహం దిశలోనే తిరుగుతూ ఉంటుంది.

ప్రశ్న 10.
ఒక వస్తువును 11.2 km.s^-1 వేగంతో లేదా అంతకంటే ఎక్కువ వేగంతో ప్రక్షిప్తం చేసినప్పుడు అది తిరిగి భూమికి చేరుకోలేదు. కారణాలతో వివరించండి.
జవాబు:
భూమిపై పలాయన వేగం (v_e) = 11.2 km/s ఏ వస్తువునైనా 11.2 km/s వేగం (లేదా) అంతకన్నా ఎక్కువ వేగంతో ప్రక్షిప్తం చేస్తే, ఆ వస్తువు ఎప్పటికీ భూమికి తిరిగిరాదు. అందుకు కారణం అది భూమ్యాకర్షణను అధిగమిస్తుంది. కాబట్టి వస్తువు ఎప్పటికీ భూమికి తిరిగిరాదు.

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 1.
గురుత్వ స్థితిజశక్తిని నిర్వచించండి. m₁, m₂ ద్రవ్యరాశులు ఉన్న రెండు కణాలకు సంబంధించిన గురుత్వ స్థితిజశక్తికి సమీకరణాన్ని ఉత్పాదించండి.
జవాబు:
గురుత్వ స్థితిజశక్తి :
ఒక వస్తువు యొక్క గురుత్వ క్షేత్రంలోని ఒక బిందువు వద్దకు మరొక వస్తువును అనంతదూరం నుండి త్వరణం లేకుండా తేవడానికి చేయవలసిన పనిని గురుత్వ స్థితిజశక్తి అంటారు.

గురుత్వ స్థితిజశక్తికి సమీకరణంను రాబట్టుట :
M ద్రవ్యరాశి, R వ్యాసార్థం గల భూమి వలన గురుత్వ క్షేత్రాన్ని తీసుకుందాం.

భూమి ద్రవ్యరాశి, దాని కేంద్రం ‘O’ వద్ద కేంద్రీకృతం అయినది అనుకుందాం.

m ద్రవ్యరాశి గల వస్తువు యొక్క గురుత్వ స్థితిజశక్తిని గురుత్వ క్షేత్రంలో p బిందువు వద్ద లెక్కిద్దాం.
ఇక్కడ OP = r మరియు r > R. OA = x మరియు AB = dx అనుకొనుము.

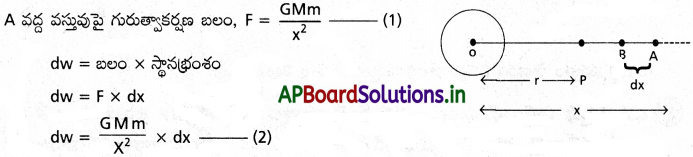
వస్తువును dx దూరం త్వరణం లేకుండా తేవడానికి జరిగిన మొత్తం పని

ఇక్కడ జరిగిన పని వస్తువులో గురుత్వ స్థితిజశక్తి రూపంలో నిల్వ ఉంటుంది.
∴ గురుత్వ స్థితిజశక్తి (U) = –\(\frac{GMm}{r}\) ………….. (4)
r దూరంలో ఉన్న m, మరియు m2 ద్రవ్యరాశులు గల రెండు కణాలలో గురుత్వ స్థితిజశక్తి
U = –\(\frac{GM_1m_2}{r}\) …………. (5) (r → ∝ అయితే, U = 0 అవుతుంది).

ప్రశ్న 2.
గురుత్వ త్వరణం (a) భూమి ఉపరితలం పైన, (b) భూమి ఉపరితలం లోపల ఎలా మారుతుందో తెలిపే సమీకరణాలను ఉత్పాదించండి.
జవాబు:
(i) ఎత్తుతోపాటు g విలువలో మార్పు :
వస్తువు భూమి ఉపరితలంపై ఉన్నప్పుడు, దూరం r = R భూమి వ్యాసార్ధం అవుతుంది.
g = \(\frac{GM}{R^2}\) ………….. (1)
ఇక్కడ G విశ్వగురుత్వ స్థిరాంకం, M = భూమి యొక్క ద్రవ్యరాశి.
భూమి ఉపరితలం నుండి, వస్తువును h ఎత్తుకు తీసుకుపోతే, r = R + h అవుతుంది.
∴ g_h = \(\frac{GM}{(R+h)^2}\) ………….. (2)

ఎత్తుకు పోవుకొలది g విలువ తగ్గుతుంది.

(ii) లోతునుబట్టి g విలువలో మార్పు :

లోతుతోపాటు g విలువ తగ్గుతుంది.

ప్రశ్న 3.
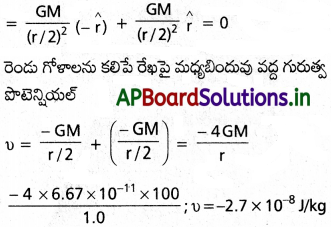
న్యూటన్ విశ్వగురుత్వాకర్షణ నియమాన్ని పేర్కొనండి. కావెండిష్ పద్ధతి ద్వారా విశ్వగురుత్వ స్థిరాంకం (G) విలువను ఎలా కనుక్కొంటారో వివరించండి.
జవాబు:

న్యూటన్ విశ్వగురుత్వాకర్షణ నియమం :
“విశ్వంలో ప్రతి వస్తువు, మరొక వస్తువును ఆకర్షించే బలం వాటి ద్రవ్యరాశుల లబ్దానికి అనులోమానుపాతంలోను, వాటిమధ్య దూరం యొక్క వర్గానికి విలోమానుపాతంలోను ఉంటుంది.

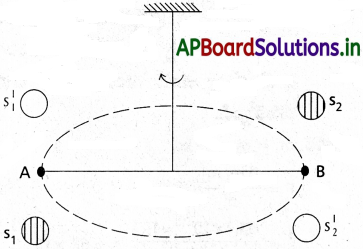
కావెండిష్ పద్ధతి ద్వారా G విలువను కనుగొనుట :

1. 1798వ సంవత్సరంలో హెన్రీ కావెండిష్ G విలువను ప్రయోగపూర్వకంగా కనుగొన్నాడు.
2. ఒక కడ్డీ AB యొక్క రెండు చివరల వద్ద రెండు చిన్న సీసపు గోళాలు అతకబడి ఉన్నాయి.
3. ఈ కడ్డీని అతిసన్నని తీగతో దృఢమైన ఆధారం నుండి వ్రేలాడదీయాలి.
4. పటంలో చూపినట్లుగా రెండు పెద్ద సీసపు గోళాలను వ్యతిరేక దిశలలో, చిన్నగోళాల దగ్గరకు తీసుకుపోవాలి.
5. పెద్దగోళాలు, వాటికి దగ్గరలో ఉన్న చిన్న గోళాలను సమాన మరియు వ్యతిరేక బలాలతో పటంలో చూపినట్లుగా ఆకర్షిస్తాయి.
6. కడ్డీ మీద ఫలితబలం లేదు, కాని కేవలం టార్క్ మాత్రమే ఉంది, ఇది స్పష్టంగా కడ్డీ పొడవుకు F రెట్లుండును. ఇక్కడ F అనునది పెద్ద గోళం మరియు దాని ప్రక్కనే ఉన్న చిన్న గోళం మధ్య ఆకర్షణ బలం.
7. ఈ టార్క్ వలన, వ్రేలాడదీసిన తీగ మెలి తిరుగుతుంది, ఆ సమయంలో తీగ యొక్క పునఃస్థాపక టార్క్, గురుత్వాకర్షణ టార్క్క సమానం.
   పునఃస్థాపక టార్క్ = τ θ ……………. (1)
   ఇక్కడ τ అనునది ప్రమాణ పురికి పునఃస్థాపక బలయుగ్మం’ రి అనునది కోణం.
8. M మరియు m ద్రవ్యరాశులు గల పెద్ద మరియు చిన్న గోళాల మధ్య దూరం d అయిన
   గురుత్వాకర్షణ బలం (F) = \(\frac{GMm}{d^2}\) …………… (2)
9. AB కడ్డీ పొడవు L. Fను Lచే గుణించగా టార్క్ ఏర్పడుతుంది. సమతాస్థితి వద్ద ఇది పునఃస్థాపక టార్క్కు సమానం.
   \(\frac{GMm}{d^2}\) = τ θ …………. (3)
   θ విలువలను పరిశీలించి, G విలువను లెక్కించవచ్చు.
   ప్రయోగపూర్వకంగా కనుగొన్న G విలువ = 6.67 × 10^-11 Nm²/ Kg².

లెక్కలు (Problems)
(విశ్వగురుత్వ స్థిరాంకం ‘G’ = 6.67 × 10^-11 Nm²kg^-2; భూమి వ్యాసార్థం ‘R’ 6400 km; భూమి ద్రవ్యరాశి ‘M_E‘ = 6 × 10²⁴ kg)

ప్రశ్న 1.
ఒక్కొక్కటి 1 kg ద్రవ్యరాశులు ఉన్న రెండు గోళాకార బంతుల్ని 1 cm దూరంలో ఉంచారు. వాటి మధ్య ఉండే గురుత్వాకర్షణ బలాన్ని కనుక్కోండి.
సాధన:
m₁ = m₂ = 1 kg, d = 1 cm = 1 × 10^-2 m

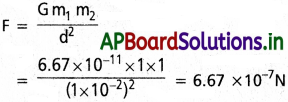
ప్రశ్న 2.
ఒక బంతి ద్రవ్యరాశి వేరొక బంతి ద్రవ్యరాశికి 4 రెట్లు ఉంది. ఈ బంతులను 10 cm దూరంలో ఉంచినప్పుడు వాటి మధ్య గురుత్వాకర్షణ బలం 6.67 × 10⁷ N అయితే ఆ బంతుల ద్రవ్యరాశు లను కనుక్కోండి.
సాధన:
m₁ = m, m₂ = 4m, d = 10 = 10 × 10^-2 m,
F = 6.67 × 10^-7 N

ప్రశ్న 3.
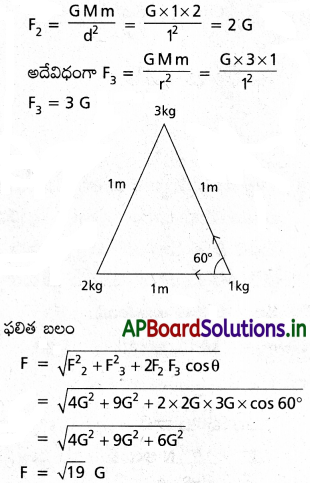
1 m భుజం పొడవు కలిగిన ఒక సమబాహు త్రిభుజం మూడు శీర్షాల వద్ద 1 kg, 2kg, 3 kg ల ద్రవ్యరాశులు కలిగిన గోళాకార బంతులను ఉంచారు. 1 kg ద్రవ్యరాశిపై 2 kg, 3kgల ద్రవ్యరాశులు ప్రయోగించే గురుత్వాకర్షణ బలాన్ని గణించండి.
సాధన:
2 kg ల ద్రవ్యరాశిపై 1 kg ద్రవ్యరాశి కలిగించే ఆకర్షణ బలం

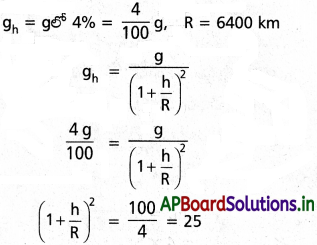
ప్రశ్న 4.
భూఉపరితలం నుంచి ఒక నిర్ణీత ఎత్తులో గురుత్వ త్వరణం భూఉపరితలంపై ఉన్న విలువలో 4% ఉంది. అయితే ఆ ఎత్తు ఎంత?
సాధన:

ప్రశ్న 5.
ఒక కృత్రిమ ఉపగ్రహం 1000 km ఎత్తులో భూమి చుట్టూ తిరుగుతున్నది దాని కక్ష్యా వడి ఎంత?
సాధన:
h = 1000 km

ప్రశ్న 6.
భూవ్యాసార్ధానికి సమానమైన ఎత్తులో ఒక కృత్రిమ ఉపగ్రహం భూమి చుట్టూ తిరుగుతున్నది. దాని (i) కక్ష్యావడి, (ii) పరిభ్రమణావర్తన కాలాలను కనుక్కోండి.
సాధన:
ఇక్కడ h = R

ప్రశ్న 7.
రెండు వస్తువుల మధ్య ఉన్న దూరాన్ని 4 m పెంచితే, వాటి మధ్య ఉన్న గురుత్వాకర్షణ బలం 36% తగ్గింది. వాటి మధ్య ఉన్న తొలిదూరం ఎంత?
సాధన:

ప్రశ్న 8.
a భుజం ఉన్న ఒక చతురస్రం ప్రతి శీర్షం వద్ద సర్వసమానమైన ద్రవ్యరాశులు mలను ఉంచారు. ఒక ద్రవ్యరాశిపై మిగతా మూడు ద్రవ్యరాశులు ప్రయోగించే గురుత్వబలాన్ని గణించండి.
సాధన:

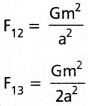
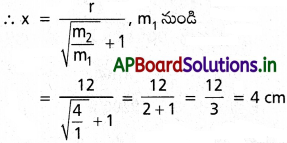
ప్రశ్న 9.
1 kg, 4 kg ద్రవ్యరాశులు ఉన్న రెండు గోళాకార బంతుల మధ్యదూరం 12 cm. 1 kg ద్రవ్యరాశి నుంచి ఎంత దూరంలో ఉన్న బిందువు వద్ద ఏ ద్రవ్యరాశి మీదనైనా పనిచేసే గురుత్వాకర్షణ బలం శూన్యం అవుతుంది.
సాధన:
m₁ = 1 kg, m₂ = 4 kg, r = 12 cm

x = 4 cm వద్ద గురుత్వాకర్షణ బలం శూన్యం.

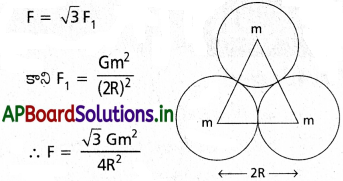
ప్రశ్న 10.
ఒక్కొక్కటి ద్రవ్యరాశి m, వ్యాసార్థం R ఉన్నట్టి మూడు ఏకరీతి గోళాలను, అందులో ప్రతి ఒకటి మిగతా రెండింటిని తాకే విధంగా అమర్చారు. వాటిలో ఏ ఒక్క గోళం పైనైనా మిగతా రెండు గోళాల వల్ల కలిగే గురుత్వాకర్షణ బల పరిమాణాన్ని లెక్కించండి.
సాధన:

ప్రశ్న 11.
రెండు కృత్రిమ ఉపగ్రహాలు వేరువేరు ఎత్తులలో భూమి చుట్టూ పరిభ్రమిస్తున్నాయి. వాటి కక్ష్యా వడుల నిష్పత్తి 2 : 1. అందులో ఒకటి 100 km ఎత్తులో ఉంటే, మరొకటి ఎంత ఎత్తులో ఉంటుంది?
సాధన:

ప్రశ్న 12.
గురుత్వ త్వరణం విలువ 8 ms ఉన్నటు వంటి ఒక ఎత్తు వద్ద ఒక కృత్రిమ ఉపగ్రహం 8 ms వడితో వృత్తాకార కక్ష్యలో తిరుగుతున్నది. భూఉపరితలం నుంచి ఉపగ్రహం ఎంత ఎత్తులో ఉన్నట్లు?
(గ్రహం వ్యాసార్థం = 6000 km)
సాధన:
v₀ = 8 km/s 8000 m/s
g_h = 8 m/s², R 6000 km
= 6000 × 10³ m

ప్రశ్న 13.
(a) భూఉపరితలం నుంచి ఒక వస్తువు పలాయన వడిని కనుక్కోండి. (b) ఒక వేళ భూమి కర్రతో గనుక తయారై ఉంటే, దాని ద్రవ్యరాశి భూమి ప్రస్తుత ద్రవ్యరాశితో 10% ఉండేది. భూమి కర్రతో తయారై ఉండి ఉంటే, పలాయన వడి ఎంత?
సాధన:

అదనపు లెక్కలు (Additional Problems)

ప్రశ్న 1.
కింది వాటికి సమాధానాలు రాయండి.
a) ఒక విద్యుదావేశాన్ని ఒక బోలు వాహకం లోపల ఉంచడం ద్వారా దానిపై విద్యుత్ బలం పనిచేయకుండా రక్షణ కల్పించవచ్చు. ఒక వస్తువును ఒక బోలు గోళం లోపల ఉంచడం ద్వారా లేదా మరే ఇతర పద్ధతిలో నైనా దానికి దగ్గరలో ఉన్న ద్రవ్యం యొక్క గురుత్వాకర్షణ బలం నుంచి రక్షించవచ్చా?
b) భూమిచుట్టూ తిరుగుతున్న ఒక చిన్న వ్యోమ నౌకలోని వ్యోమగామి గురుత్వాకర్షణ బలం ఉనికిని గుర్తించలేడు. భూమి చుట్టూ తిరుగుతున్న వ్యోమనౌక చాలా పెద్దదిగా ఉంటే గురుత్వాకర్షణ బలం ఉనికిని గుర్తించగలనని అతడు ఆశించ వచ్చా?
c) సూర్యుని మూలంగా భూమిపై కలిగే గురుత్వ త్వరణం, చంద్రుని మూలంగా భూమిపై కలిగే గురుత్వ త్వరణాలను పోల్చినప్పుడు చంద్రుని ఆకర్షణ కంటే సూర్యుని ఆకర్షణ ఎక్కువగా ఉంటుందని స్పష్టమవుతుంది. (తరువాతి అభ్యాసాలలో లభ్యమయ్యే సమాచారాన్ని వినియోగించుకొని మీరీ విషయాన్ని స్వయంగా సరిచూసుకోవచ్చు).
సాధన:
a) దగ్గరలో ఉన్న ద్రవ్యం నుండి, వస్తువుపై గురుత్వాకర్షణ ప్రభావం లేకుండా రక్షించలేము. అందుకు కారణం దగ్గరలో ఉన్న ద్రవ్యం వల్ల, వస్తువుపై పనిచేసే గురుత్వాకర్షణ బలాలు, మరొక ద్రవ్యం వల్ల పనిచేసే వాటిపై ఆధారపడవు. విద్యుత్ బలాలలో గురుత్వ బలాల వలె సాధ్యం కాదు.

b) అవును, భూమి చుట్టూ పరిభ్రమించే అంతరిక్ష నౌక పరిమాణం పెద్దది అయినా, అంతరిక్ష నౌక లోపల ఉన్న వ్యోమగామి gలో మార్పును కనుగొనవచ్చు.

c) ఆటుపోటులు, దూరం యొక్క ఘనానికి విలోమాను పాతంలో ఉంటాయి. చంద్రుడి నుండి సముద్రం వరకు దూరం, సూర్యుడి నుండి సముద్రం వరకు దూరం కన్నా తక్కువ. అందువల్ల సూర్యుడి వల్ల కన్నా చంద్రుడి ప్రభావం ఆటుపోటులపై ఎక్కువ.

ప్రశ్న 2.
సరియైన ప్రత్యామ్నాయాన్ని ఎంచుకోండి.
a) ఉన్నతాంశం పెరుగుతున్నకొద్దీ గురుత్వ త్వరణం పెరుగుతుంది/తగ్గుతుంది.
b) లోతు పెరుగుతున్న కొద్దీ గురుత్వ త్వరణం పెరుగుతుంది/తగ్గుతుంది. (భూమిని ఏకరీతి సాంద్రత కలిగిన గోళంగా పరిగణించండి.)
c) భూమి ద్రవ్యరాశి / వస్తువు ద్రవ్యరాశిపై గురుత్వ త్వరణం ఆధారపడి ఉండదు.
d) భూకేంద్రం నుంచి r₁, r₂ దూరాలలో ఉన్న రెండు బిందువుల మధ్య స్థితిజశక్తి భేదానికి సూత్రం −GMm (1/r₂ – 1/r₁) అనేది సూత్రం mg(r₂ – r₁) కంటే ఎక్కువ/తక్కువ.
సాధన:
a) తగ్గుతుంది
b) తగ్గుతుంది
c) వస్తువు యొక్క ద్రవ్యరాశి
d) అధికం

ప్రశ్న 3.
సూర్యుని చుట్టూ భూమి కంటే రెండు రెట్లు ఎక్కువ వడితో తిరిగే ఒక గ్రహం ఉందను కొందాం. భూమితో పోల్చినప్పుడు దాని కక్ష్యా పరిమాణం (orbital size) ఎంత ఉంటుంది?
సాధన:

ప్రశ్న 4.
బృహస్పతి గ్రహానికి ఉన్న ఒకానొక ఉపగ్రహం ఇయో (Io) కక్ష్యావర్తన కాలం 1.769 రోజులు. కక్ష్యావ్యాసార్ధం 4.22 × 10⁸m అయితే బృహస్పతి ద్రవ్యరాశి, సూర్యుని ద్రవ్యరాశిలో దాదాపు వెయ్యవ వంతు ఉంటుందని చూపండి.
సాధన:
బృహస్పతి యొక్క ఉపగ్రహం, కక్ష్యావర్తన కాలం,
T₁ = 1.769 రోజులు = 1.769 × 24 × 60 × 60
ఉపగ్రహం యొక్క కక్ష్యా వ్యాసార్థం.
T₁ = = 4.22 × 10⁸ m
బృహస్పతి ద్రవ్యరాశి

భూమి, సూర్యుడి చుట్టూ తిరిగే ఆవర్తన కాలం
T = 1 సంవత్సరం = 365.25 × 24 × 60 × 60
కక్ష్యా వ్యాసార్థం, r = 1 A.U = 1.496 × 10¹¹m

ప్రశ్న 5.
ఒక్కొక్కటి సౌర ద్రవ్యరాశికి సమానమైన ద్రవ్యరాశి ఉన్న 2.5 × 10¹¹నక్షత్రాలు మన నక్షత్ర మండలం (galaxy)లో ఉన్నాయని ఊహిద్దాం. నక్షత్రమండల కేంద్రం నుంచి 50,000 కాంతి సంవత్సరాల దూరంలో ఉన్న ఒక నక్షత్రం ఒక పూర్తి పరిభ్రమణానికి ఎంత కాలం తీసుకొంటుంది? మన నక్షత్ర మండలమైన పాలపుంత వ్యాసం 10⁵ ly (ly = light year = కాంతి సంవత్సరం) గా తీసుకోండి.
సాధన:
ఇక్కడ r = 50,000 కాంతి సంవత్సరాలు
= 50,000 × 9.46 × 10¹⁵ m
= 4.73 × 10²⁰ m
M = 2.5 × 10¹¹ సూర్యుడి ద్రవ్యరాశి
= 2.5 × 10¹¹ × 2 × 10³⁰ kg
= 5 × 10⁴¹ kg

ప్రశ్న 6.
సరియైన ప్రత్యామ్నాయాన్ని ఎంచుకోండి.
a) స్థితిజశక్తి శూన్య విలువను అనంత దూరం వద్ద తీసుకొంటే, పరిభ్రమిస్తున్న ఉపగ్రహం మొత్తం శక్తి దాని గతిజశక్తి/స్థితిజశక్తికి రుణాత్మకం.
b) పరిభ్రమిస్తున్న ఒక కృత్రిమ ఉపగ్రహాన్ని భూమ్యాకర్షణ ప్రభావానికి ఆవల వరకు సంధించడానికి అవసరమయ్యే శక్తి కృత్రిమ ఉపగ్రహం ఉన్న ఎత్తులోనే నిశ్చలంగా ఉన్న ఒక ప్రక్షేపకాన్ని భూమ్యాకర్షణ ప్రభావా న్నుంచి ప్రక్షిప్తం చెయ్యడానికి అవసరమయ్యే శక్తి కంటే ఎక్కువ/తక్కువ.
జవాబు:
a) గతిజ శక్తి
b) తక్కువ

ప్రశ్న 7.
భూమి నుంచి ఒక వస్తువు పలాయన వడి ఈ అంశాలపై ఆధారపడుతుందా? (a) వస్తువు ద్రవ్యరాశి, (b) వస్తువు ప్రక్షిప్తం చేసిన స్థానం, (c) ప్రక్షిప్తం చేసిన దిశ, (d) వస్తువును ప్రక్షేపించిన స్థానం ఎత్తు.
జవాబు:
పలాయన వేగం వస్తువు ద్రవ్యరాశిపై, ప్రక్షిప్త వేగంపై ఆధారపడదు. ఇది ప్రక్షిప్తం చేసిన బిందువు వద్ద గురుత్వ పొటెన్షియల్పై ఆధారపడుతుంది. ఈ పొటెన్షియల్ అక్షాంశం మరియు బిందువు ఎత్తుపై స్వల్పంగా ఆధారపడుతుంది. కాబట్టి పలాయన వేగం ఈ మూడు అంశాలపై స్వల్పంగా ఆధారపడుతుంది.

ప్రశ్న 8.
ఒక తోకచుక్క సూర్యుని చుట్టూ ఒక అత్యధిక అర్థగురు అక్షంగల దీర్ఘవృత్తాకార కక్ష్యలో తిరుగుతున్నది. ఈ తోకచుక్క కక్ష్య యావత్తు ఈ రాశులు స్థిరంగా ఉంటాయా? (a) రేఖీయ వడి, (b) కోణీయ వడి, (c) కోణీయ ద్రవ్యవేగం, (d) గతిజశక్తి, (e) స్థితిజశక్తి, (f) మొత్తం యాంత్రిక శక్తి. తోకచుక్క సూర్యునికి దగ్గరగా వచ్చినప్పుడు అది ఏమైనా ద్రవ్యరాశిని కోల్పోతే ఆ ద్రవ్యరాశిని ఉపేక్షించండి.
జవాబు:
సూర్యుడి చుట్టూ పరిభ్రమించే తోకచుక్క కోణీయ ద్రవ్యవేగం మరియు అన్ని స్థానాల వద్ద మొత్తం శక్తి స్థిరంగా ఉంటుంది. కాని అన్ని స్థానాల వద్ద మిగిలిన రాశులు మారతాయి.

ప్రశ్న 9.
ఈ లక్షణాలలో ఏది రోదసిలోని వ్యోమగామికి హాని కలిగించవచ్చు. (a) కాళ్ళవాపు, (b) ముఖం వాపు, (c) తలనొప్పి, (d) దిగ్విన్యాస (orienta- tional problem) సమస్య.
జవాబు:
a) గురుత్వాకర్షణ వల్ల సాధారణ స్థితిలో మన కాళ్ళు, శరీరం యొక్క బరువును మోస్తాయి. అంతరిక్షంలో అంతరిక్ష యాత్రికుడు భారరహితంగా ఉంటాడు. కాబట్టి అతని పాదాలు పనిచేయకపోయినా అతని పనితీరుపై ప్రభావం చూపదు.

b) భారరహితస్థితిలో, వ్యోమగామి ముఖం ఉబ్బుతుంది. అలాగే కళ్ళు, చెవులు, ముక్కు, నోరు మొదలగునవి. లోపలకు పీక్కుపోతాయి. అందువలన అంతరిక్షంలో చూడటం, వినడం, తినడం, వాసన చూడటంపై ప్రభావం ఉంటుంది.

c) భూమిపై ఉన్నప్పటి వలెనే అంతరిక్షంలో కూడా వ్యోమగామికి తలనొప్పి ఒకేవిధంగా ఉంటుంది.

d) అంతరిక్షం కూడా ఓరియంటేషన్ కలిగి ఉండుటవల్ల అంతరిక్షంలో నిర్దేశ చట్రాలను మనం కలిగి ఉన్నాము. కాబట్టి అంతరిక్షంలో వ్యోమగామిపై ఓరియంటేషన్ ప్రభావం ఉంటుంది.

ప్రశ్న 10.
ఈ దిగువ ఉన్న రెండు అభ్యాసాల్లో ఇచ్చిన వాటి నుంచి సరియైన సమాధానాన్ని ఎంచుకోండి. ఏకరీతి ద్రవ్యరాశి సాంద్రత (mass density) కలిగిన ఒక అర్థగోళాకార కర్పరం కేంద్రం దగ్గర ఉండే గురుత్వాకర్షణ తీవ్రత దిశ పటంలో బాణం గుర్తు సూచించిన విధంగా ఉంది. (i) a, (ii) b, (iii) c, (iv) 0.

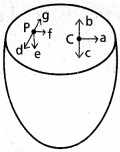
జవాబు:
గోళాకార కర్పరం (బోలు గోళం)లో గురుత్వ పొటెన్షియల్ లోపలి వైపు అన్ని బిందువుల వద్ద స్థిరం. కాబట్టి అన్ని బిందువుల వద్ద గురుత్వ పొటెన్షియల్ ప్రవణత బోలు గోళం లోపల శూన్యం [అనగా v స్థిరం, \(\frac{dv}{dt}\) = 0]. గురుత్వ తీవ్రత, గురుత్వ పొటెన్షియల్ గ్రేడియంట్ రుణ విలువకు సమానం. కావున గురుత్వ తీవ్రత అన్ని బిందువుల వద్ద శూన్యం.

బోలుగోళం లోపల ఏ బిందువు వద్దనైనా గురుత్వాకర్షణ బలాలు సౌష్టంగా ఉంటాయి. పై అర్థభాగాన్ని తొలగిస్తే, కేంద్రం Q వద్ద ఉన్న కణంపై పనిచేసే గురుత్వాకర్షణ బలం (లేదా) P బిందువు వద్ద కూడా గురుత్వ తీవ్రత దిశలోనే క్రిందకు పని చేస్తాయి. అనగా ఒక బిందువు వద్ద గురుత్వక్షేత్ర తీవ్రత, ఆ బిందువు వద్ద ప్రమాణ ద్రవ్యరాశిపై గురుత్వాకర్షణ బలం అవుతుంది. కాబట్టి గురుత్వ క్షేత్ర తీవ్రత, కేంద్రం వద్ద ఁ దిశలో ఉంటుంది. అనగా (iii) వ ఆప్షన్ సరియైనది.

ప్రశ్న 11.
పై సమస్యలో ఒకానొక యాదృచ్ఛిక బిందువు Pవద్ద ఉండే గురుత్వాకర్షణ తీవ్రత దిశను బాణం గుర్తుతో సూచించడమైంది.
(i) d, (ii) e, (iii) f, (iv) g.
జవాబు:
P వద్ద గురుత్వక్షేత్ర తీవ్రత ఆ దిశలో ఉంటుంది. కావున (ii) సరియైనది.

ప్రశ్న 12.
భూమి నుంచి సూర్యుని వైపు దూసుకెళ్లే విధంగా ఒక రాకెట్ను పేల్చారు. భూకేంద్రం నుంచి ఎంత ఎత్తులో రాకెట్పై పనిచేసే గురుత్వాకర్షణ బలం శూన్యమవుతుంది? సూర్యుని ద్రవ్యరాశి 2 × 10³⁰ kg, భూమి ద్రవ్యరాశి = 6 × 10²⁴ kg మిగతా ఉపగ్రహాల ప్రభావాన్ని ఉపేక్షించండి. (కక్ష్యా వ్యాసార్థం = 1.5 × 10¹¹m).
సాధన:
M_s = 2 × 10³⁰kg, M_e = 6 × 10²⁴ kg;
r = 1.5 × 10¹¹ m

x అనునది భూమి మరియు సూర్యుడి వల్ల రాకెట్పై గురుత్వాకర్షణ బలం సమానం మరియు వ్యతిరేకం అయిన చోట భూమి నుండి బిందువు వరకు దూరం. సూర్యుడి నుండి రాకెట్ వరకు దూరం = r – x. రాకెట్ ద్రవ్యరాశి m.

ప్రశ్న 13.
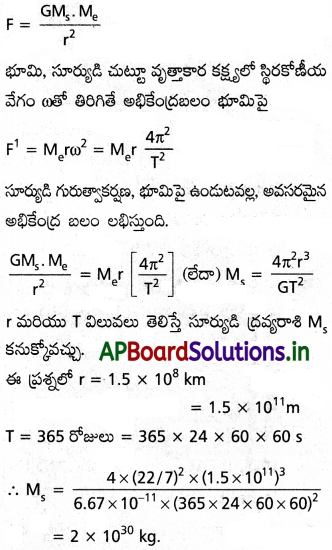
సూర్యుని ఎలా తూచుతారు? అంటే దాని ద్రవ్యరాశిని అంచనా వేయండి. సూర్యుని చుట్టూ భూమి సరాసరి కక్ష్యా వ్యాసార్ధం 1.5 × 10⁸ km.
సాధన:
సూర్యుడి ద్రవ్యరాశి కనుక్కోవడానికి, దాని ఏదైనా ఒక గ్రహం ఆవర్తన కాలం T అవసరం (భూమిని తీసుకుందాం). M_s, M_e సూర్యుడు, భూమి ద్రవ్యరాశులు మరియు r అనునది సూర్యుడి నుండి, భూమి కక్ష్యా వ్యాసార్థం. సూర్యుడి వలన, భూమిపై గురుత్వాకర్షణ బలం

ప్రశ్న 14.
శని సంవత్సరం భూసంవత్సరానికి 29.5 రెట్లు ఉంటుంది. సూర్యుని నుంచి భూమి 1.50 × 10⁸ km దూరంలో ఉన్నట్లయితే సూర్యుని నుంచి శనిగ్రహం దూరం ఎంత?
సాధన:
ఇక్కడ T_s = 29.5 T_e; R_e = 1.5 × 10⁸ km; R_s = ?

ప్రశ్న 15.
భూఉపరితలంపై ఒక వస్తువు 63 N బరువు ఉంటుంది. భూవ్యాసార్థానికి సగం ఎత్తులో భూమి పరంగా ఆ వస్తువుపై పనిచేసే గురుత్వాకర్షణ బలం ఎంత?
సాధన:
వస్తువు యొక్క భారం = mg = 63 N
h ఎత్తు వద్ద g విలువ,

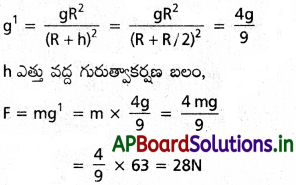
ప్రశ్న 16.
భూమిని ఒక ఏకరీతి ద్రవ్యరాశి సాంద్రత గల గోళంగా పరిగణిస్తే, భూఉపరితలంపై 250 N భారం కలిగిన వస్తువు భూకేంద్రం వైపు పోతున్న ప్పుడు కేంద్రానికి సగం దూరంలో ఎంత భారం కలిగి ఉంటుంది?
సాధన:

ప్రశ్న 17.
భూఉపరితలం నుంచి ఒక రాకెట్ను 5 kms^-1 వడితో నిట్టనిలువుగా పేల్చారు. భూమికి తిరిగి వచ్చేలోగా అది భూమి నుంచి ఎంత దూరం పోతుంది? భూమి ద్రవ్యరాశి = 6.0 × 10²⁴ kg ; భూమి సగటు వ్యాసార్థం = 6.4 × 10⁶ m; G = 6.67 × 10^-11 N m² kg^-2.
సాధన:
భూమిపై నుండి రాకెట్ υ వేగంతో పైకి పేల్చబడింది.
దాని వేగం సున్నా అయ్యేసరికి అది h ఎత్తుకు చేరినది అనుకొనుము.
భూమిపై రాకెట్ మొత్తం శక్తి = K.E + P.E

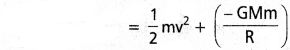
ప్రశ్న 18.
భూఉపరితలంపై ఒక ప్రక్షేపకం పలాయన వడి 11.2 kms^-1. దీనికి మూడు రెట్లు వేగంతో ఒక వస్తువును ప్రక్షిప్తం చేశారు. భూమి నుండి సుదూరంలో (అంటే అనంతదూరంలో) వస్తువు వడి ఎంత? సూర్యుడు, ఇతర గ్రహాల ఉనికిని విస్మరించండి.
సాధన:
ఇక్కడ υe = 11.2 kms^-1,
వస్తువు ప్రక్షిప్త వేగం υ = 3υe. ప్రక్షేపకం ద్రవ్యరాశి m, భూమి నుండి దూరంగా పోయినపుడు ప్రక్షేపకం వేగం υ₀. శక్తి నిత్యత్వ నియమం ప్రకారం

ప్రశ్న 19.
భూఉపరితలం నుంచి 400 km ఎత్తున ఒక కృత్రిమ ఉపగ్రహం పరిభ్రమిస్తుంది. భూమి గురుత్వాకర్షణ ప్రభావం నుంచి కృత్రిమ ఉపగ్రహాన్ని తప్పించడానికి ఎంత శక్తిని వెచ్చించాలి? కృత్రిమ ఉపగ్రహం ద్రవ్యరాశి = 200 kg; భూమి ద్రవ్యరాశి = 6.0 × 10²⁴ kg; భూవ్యాసార్థం = 6.4 × 1⁶ m; G = 6.67 × 10^-11 Nm²kg ^-2.
సాధన:
h ఎత్తులో తిరుగుతున్న ఉపగ్రహం మొత్తం శక్తి

ప్రశ్న 20.
ఒక్కొక్కటి సూర్యుని ద్రవ్యరాశి (= 2 × 10³⁰ kg) కి సమానమైన ద్రవ్యరాశి కలిగిన రెండు నక్షత్రాలు ముఖాముఖీ అభిఘాతం చెందేవిధంగా పరస్పరం సమీపిస్తున్నాయి. వాటి మధ్యదూరం 10⁹ kmగా ఉన్నప్పుడు వాటి వడులు విస్మరింప దగినవిగా ఉన్నాయి. అవి ఏ వడితో అభిఘాతం చెందుతాయి? ప్రతి నక్షత్రం వ్యాసార్ధం 10⁴ km. పరస్పరం అభిఘాతం చెందేంత వరకు అవి విరూపణ చెందకుండా ఉంటాయని అనుకొందాం. (తెలిసిన G విలువ ఉపయోగించండి.)
సాధన:
ప్రతి నక్షత్రం ద్రవ్యరాశి, M = 2 × 10³⁰ kg
రెండు నక్షత్రాల మధ్యదూరం, r = 10⁹ = 10¹²
వ్యవస్థ యొక్క తొలి స్థితిజశక్తి = –\(\frac{GMM}{r}\)

ప్రశ్న 21.
ఒక క్షితిజ సమాంతర బల్లపై ఒక్కొక్కటి 100 kg ద్రవ్యరాశి, 0.1 m వ్యాసార్ధం ఉన్న రెండు బరువైన గోళాలు 1.0 m దూరంలో ఉన్నాయి. ఆ గోళ కేంద్రాలను కలిపే రేఖ మధ్యబిందువు వద్ద గురుత్వాకర్షణ బలం, పొటెన్షియల్ ఎంత ఉంటాయి? ఆ బిందువు వద్ద ఉంచిన వస్తువు సమతాస్థితిలో ఉంటుందా? ఒకవేళ ఉంటే, ఆ వస్తువు స్థిర సమతాస్థితిలో ఉంటుందా? అస్థిర సమతాస్థితిలో ఉంటుందా?
సాధన:
రెండు గోళాలను కలిపే రేఖపై మధ్యబిందువు వద్ద గురుత్వక్షేత్రం

మధ్యబిందువు వద్ద వస్తువుపై ప్రభావిత బలం శూన్యం. కాబట్టి వస్తువు సమతాస్థితిలో ఉంది. మాధ్యమిక స్థానం నుండి వస్తువును కొద్దిగా స్థానభ్రంశం చెందిస్తే, ఇది మరలా తిరిగి మాధ్యమిక స్థానానికి రాదు. కాబట్టి వస్తువు అస్థిర సమతాస్థితిలో ఉంటుంది.

ప్రశ్న 22.
మీరు నేర్చుకున్నట్లుగా, ఒక భూస్థావర ఉపగ్రహం భూమి ఉపరితలం నుంచి 36,000 km ఎత్తులో ఉన్న కక్ష్యలో భూమి చుట్టూ పరిభ్రమిస్తుంది. ఉపగ్రహం ఉన్న ప్రదేశంలో భూమి గురుత్వం మూలంగా కలిగే పొటెన్షియల్ ఎంత? (అనంత దూరం వద్ద పొటెన్షియల్ సున్నాగా తీసుకోండి) భూమి ద్రవ్యరాశి = 6.0 × 10²⁴ kg, భూవ్యాసార్థం = 6400 km).
సాధన:
భూమి నుండి h ఎత్తులో గురుత్వ పొటెన్షియల్

ప్రశ్న 23.
సూర్యుని ద్రవ్యరాశికి 2.5 రెట్లు ద్రవ్యరాశిని కలిగి, 12 km పరిమాణానికి కుంచించుకు పోయిన ఒక నక్షత్రం సెకనుకు 1.2 పరిభ్రమణాల వడితో తిరుగుతుంది. (ఈ రకమైన నక్షత్రాలను ‘న్యూట్రాన్ నక్షత్రాలు’ అంటారు. pulsars అని పిలవబడే కొన్ని ఖగోళ వస్తువులు ఈ కోవకు చెందినవే). ఆ నక్షత్ర మధ్యరేఖ (equator) పై ఉంచిన వస్తువు గురుత్వాకర్షణ వల్ల దానికే అతుక్కొని పోతుందా?
(సూర్యుని ద్రవ్యరాశి = 2 × 10³⁰ kg)
సాధన:
నక్షత్రం గురుత్వాకర్షణ వల్ల వస్తువు నిలబడి ఉంటుంది. అపకేంద్ర త్వరణం కన్నా గురుత్వ త్వరణం అధికం.

అపకేంద్ర త్వరణం (g) = rω²
= r(2πv)²
= 12000 (2π × 1.5)²
= 1.1 × 10⁶ ms^-2
g > rω² కాబట్టి వస్తువు నక్షత్రంపై నిలిచి ఉంది.

ప్రశ్న 24.
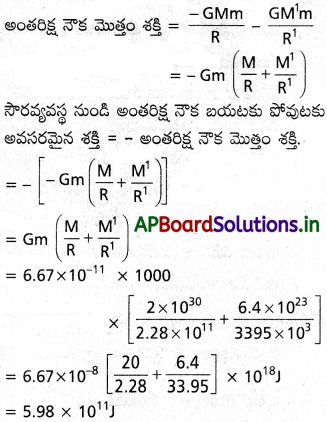
అంగారక గ్రహంపై ఒక వ్యోమనౌక నిలిచి ఉంది. సౌర వ్యవస్థకు ఆవల దానిని పంపించాలంటే వ్యోమనౌకకు ఎంత శక్తిని వినియోగించాలి? వ్యోమనౌక ద్రవ్యరాశి = 1000 kg ; సూర్యుని ద్రవ్యరాశి = = 2 × 10³⁰ kg ; అంగారకుని ద్రవ్యరాశి = 6.4 × 10²³ kg; అంగారకుని వ్యాసార్థం 3395 km ; అంగారకుని కక్ష్యా వ్యాసార్థం 2.28 × 10⁸ km; G = 6.67 × 10^-11 Nm² kg^-2.
సాధన:
అంగారక గ్రహం కక్ష్యా వ్యాసార్థం R అనుకొనుము. మరియు R’ అంగారక గ్రహం వ్యాసార్థం. సూర్యుడి ద్రవ్యరాశి M మరియు అంగారకుడి ద్రవ్యరాశి M. అంతరిక్ష నౌక ద్రవ్యరాశి m అయితే
సూర్యుడి గురుత్వాకర్షణ వల్ల అంతరిక్ష నౌక యొక్క స్థితిజ శక్తి = \(\frac{-GMm}{R}\)

అంగారక గ్రహం గురుత్వాకర్షణ వల్ల అంతరిక్ష నౌక స్థితిజ శక్తి = \(\frac{GM^1m}{R^1}\)
అంతరిక్ష నౌక గతిజశక్తి శూన్యం. కాబట్టి

ప్రశ్న 25.
అంగారక గ్రహం ఉపరితలం నుంచి 2 kms వడితో ఒక రాకెట్ను నిట్టనిలువుగా పేల్చారు. అంగారక గ్రహ వాతావరణ నిరోధం వల్ల దాని తొలిశక్తిలో 20% హరించుకుపోతే, అంగారక గ్రహానికి అది తిరిగి వచ్చేలోగా దాని ఉపరితలం నుంచి ఆ రాకెట్ ఎంత దూరం వరకు దూసుకెళ్ల గలుగుతుంది?
అంగారకుని ద్రవ్యరాశి = 6.4 × 10²³ kg.
అంగారకుని వ్యాసార్థం = 3395 km;
G = 6.67 × 10^-11 N m²kg^-2.
సాధన:
రాకెట్ ద్రవ్యరాశి = m, అంగారకుడి ద్రవ్యరాశి = M
అంగారకుడి వ్యాసార్థం = R
రాకెట్ తొలివేగం v

రాకెట్ అంగారకుడి ఉపరితలం నుండి, h ఎత్తుకు చేరితే, దాని గతిజ శక్తి శూన్యం మరియు స్థితిజ శక్తి

సాధించిన సమస్యలు (Solved Problems)

ప్రశ్న 1.
పటంలో చూపిన విధంగా సూర్య సమీప బిందువు P వద్ద గ్రహం వడి υ_p అని, సూర్యుడు-గ్రహం మధ్యదూరం SP ని r_p స్త్రీ అని అనుకొందాం. ఈ {r_p, v_p}లను సూర్య సుదూర

బిందువు వద్ద వాటికి అనురూపమైన రాశులు (r₄, υ₄) లతో అనుసంధానించండి. BAC, CPB పథాలను పూర్తి చేయడానికి గ్రహం ఒకే సమయాన్ని తీసుకొంటుందా?
సాధన:
జాగ్రత్తగా పరిశీలిస్తే, r_p, v_p లు పరస్పరం లంబంగా ఉంటాయని తెలుస్తుంది. అందువల్ల P వద్ద కోణీయ ద్రవ్యవేగ పరిమాణం L_p = m_pr_pυ_p అవుతుంది. అదేవిధంగా, L_A = m_pr_AV_A అవుతుంది.
కోణీయ ద్రవ్యవేగ నిత్యత్వ నియమాన్ని అనుసరించి,
m_Pr_Pυ_P = m_Pr_Aυ_A

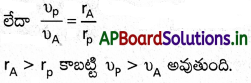
పటంలో దీర్ఘవృత్తం, సదిశ వ్యాసార్థాలు SB, SC ల వల్ల బంధితమైన క్షేత్ర వైశాల్యం SBAC, వైశాల్యం SBPC కంటే ఎక్కువగా ఉంది. కెప్లర్ రెండవ నియమం ప్రకారం సమాన కాలవ్యవధులలో గ్రహం సమాన వైశాల్యాలను చిమ్ముతుంది. కాబట్టి గ్రహం CPB మార్గాన్ని పూర్తి చేయడాని కంటే, BAC మార్గాన్ని పూర్తిచేయడానికి ఎక్కువ సమయాన్ని తీసుకొంటుంది.

ప్రశ్న 2.
ఒక సమబాహు త్రిభుజం ABC మూడు శీర్షాల వద్ద ఒక్కొక్కటి m kg ద్రవ్యరాశి ఉన్న మూడు వస్తువులు అమర్చి ఉన్నాయి.
a) ఆ త్రిభుజ కేంద్రాభం O వద్ద 2m ద్రవ్యరాశి ఉన్న వస్తువు ఉంచితే, దానిపై పనిచేసే బలం ఎంత?
b) శీర్షం A వద్ద ఉన్న వస్తువు ద్రవ్యరాశిని రెండు రెట్లు చేస్తే అప్పుడు దానిపై పనిచేసే బలం ఎంత?
AG = BO = CO = 1 mగా తీసుకోండి. (పటంను పరిశీలించండి.)
సాధన:
(a) OC, ధన x-అక్షం మధ్యకోణం 30° అదేవిధంగా OB రుణ X-అక్షం మధ్య కోణం కూడా 30°. సదిశా రూపంలో, విడివిడిగా బలాలను కిందివిధంగా రాయవచ్చు.

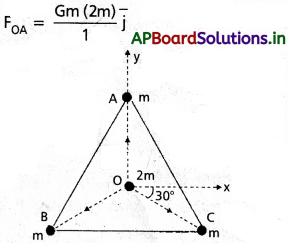
∆ABC మూడు శీర్షాల వద్ద సమాన ద్రవ్యరాశి ఉన్న మూడు వస్తువులను ఉంచారు. త్రిభుజ కేంద్రాభం వద్ద 2m ద్రవ్యరాశి ఉన్న వస్తువును ఉంచడమైంది.

O వద్ద ఉన్న 2m ద్రవ్యరాశిపై పనిచేసే ఫలితబలం F_R అయితే, అధ్యారోపణ సూత్రం, సదిశా సంకలన నియమాల ప్రకారం,

ఈ సమస్యకు ఇంకోరకంగా సులభంగా సాధించవచ్చు. సౌష్టవం (symmetry) ప్రాతిపదికగా విశ్లేశిస్తే ఫలిత బలం శూన్యం అయి తీరాలని, మనం సులభంగానే అంచనావేయవచ్చు.
(b)సౌష్టవం పరంగా విశ్లేషిస్తే, బలం X అంశం రద్దవుతుంది.

ప్రశ్న 3.
భుజం పొడవు 1 గా ఉన్న ఒక చతురస్రం యొక్క ప్రతీ శీర్షం వద్ద ఒక్కో కణాన్ని ఉంచితే, ఆ నాలుగు కణాల వ్యవస్థ మొత్తం స్థితిజశక్తిని కనుక్కోండి. ఆ చతురస్ర కేంద్రం వద్ద పొటెన్షియల్ను కూడా గణించండి.
సాధన:
భుజం పొడవు ఉన్నటువంటి ఒక చతురస్రం ప్రతీ శీర్షం వద్ద m ద్రవ్యరాశి ఉన్న ఒక్కో కణాన్ని ఉంచామనుకోండి. పటంని పరిశీలిస్తే, l దూరంలో నాలుగు ద్రవ్యరాశుల జతలు, √2l దూరంలో కర్ణాల పరంగా రెండు ద్రవ్య రాశుల జతలూ మనకు కనిపిస్తాయి. కాబట్టి,

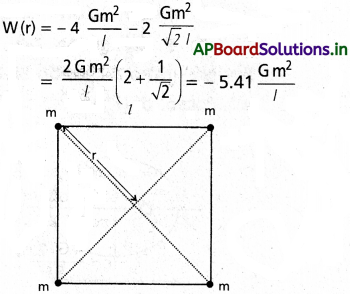
చతురస్ర కేంద్రం U(r) వద్ద గురుత్వాకర్షణ స్థితిజ శక్తి
(r = √2// 2) అయితే,
U(r) = -4√2 \(\frac{GM}{l}\)

ప్రశ్న 4.
పటంలో చూపించిన విధంగా ఒకే వ్యాసార్థం R, భిన్న ద్రవ్యరాశులు M, 4Mలను కలిగిన రెండు ఏకరీతి ఘనగోళాలను వాటి కేంద్రాల మధ్య ఎడం 6R ఉండేటట్లుగా అమర్చారు. రెండు గోళాలను స్థిరంగా పట్టి ఉంచారు. m ద్రవ్యరాశి ఉన్న ఒక ప్రక్షేపకాన్ని M ద్రవ్యరాశి ఉన్న గోళం ఉపరితలం నుంచి నేరుగా రెండవ గోళ కేంద్రం వైపుకు విసిరినప్పుడు ప్రక్షేపకం రెండవ గోళం ఉపరితలాన్ని చేరుకోవాలంటే ప్రక్షేపకానికి ఉండ వలసిన కనిష్ఠ వడి vకి సమీకరణాన్ని రాబట్టండి.

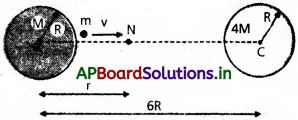
సాధన:
ప్రక్షేపకం రెండు గోళాలకు సంబంధించిన రెండు పరస్పర వ్యతిరేక గురుత్వాకర్షణ బలాల ప్రభావానికి లోనవుతుంది. ఈ రెండు బలాలు ఒకదానికొకటి సరిగ్గా ఏ స్థానం వద్ద రద్దు చేసుకొంటాయో ఆ స్థానాన్ని తటస్థ బిందువు N (పటం చూడండి)గా నిర్వచిస్తాం.
ఒకవేళ ON = r అయితే,

O నుంచి తటస్థ బిందువుకు ఉన్న దూరం = – 6R అవ ఈ ఉదాహరణలో వర్తించదు. కాబట్టి ON = r = 2Rను మాత్రమే పరిగణనలోకి తీసుకోవాలి. మొదటగా మనం ప్రక్షేపకాన్ని Nను చేరుకొనేంత వడితో విసిరితే సరిపోతుంది. ఆ తరవాత 4M ద్రవ్యరాశి ఉన్న గోళం యొక్క అత్యధిక గురుత్వాకర్షణ బలమే దానిని తనవైపు లాక్కోవడానికి సరిపోతుంది. M ద్రవ్యరాశి ఉన్న గోళ ఉపరితలం వద్ద యాంత్రిక శక్తి E అయితే,

తటస్థ బిందువు N వద్ద ప్రక్షేపకం వడి సున్నాను సమీపిస్తుంది. N వద్ద ప్రక్షేపకం యాంత్రిక శక్తి యావత్తూ పూర్తిగా దాని స్థితిజ శక్తి రూపంలోనే ఉంటుంది. N వద్ద ప్రక్షేపకం యాంత్రిక శక్తి E_N అయితే

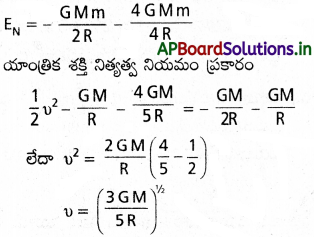
ప్రశ్న 5.
కుజ గ్రహానికి ఫోబోస్ (phobos), డెల్మోస్ (delmos) అనే రెండు ఉపగ్రహాలు ఉన్నాయి. (i) ఫోటాస్ కక్ష్యావర్తన కాలం 7 గం. 39 నిమిషాలు. దాని కక్ష్యా వ్యాసార్థం 9.4 × 10³ km. కుజుని ద్రవ్యరాశిని కనుక్కోండి. (i) భూమి, కుజుడూ సూర్యుని చుట్టూ వృత్తాకార కక్ష్యల్లో, కుజుని కక్ష్యా వ్యాసార్ధం భూకక్ష్యా వ్యాసార్థానికి 1.52 రెట్లు ఉండేవిధంగా తిరుగుతున్నాయనుకొందాం. అప్పుడు ఒక కుజ సంవత్సరంలో ఎన్ని రోజు లుంటాయి?
సాధన:
(i) సమీకరణం T’ = K(R_E + h)³ లో భూమి ద్రవ్యరాశికి బదులుగా కుజుని ద్రవ్యరాశి M_mను ప్రతిక్షేపిస్తే,

ఇక్కడ R_MS కుజునికి, సూర్యునికి మధ్యదూరం, R_ES’ భూమికి సూర్యునికి మధ్యదూరం
∴ TM = (1.52)^3/2 × 365 = 684 రోజులు

ప్రశ్న 6.
భూమిని తూచడం (Weighing the Earth) ; కింది సమాచారాన్ని మీకిచ్చారు :
g = 9.81 ms^-2; R_E = 6.37 ×10⁶ m చంద్రునికి ఉన్న దూరం R = 3.84 ×10⁸ m, చంద్రుని పరిభ్రమణావర్తన కాలం 27.3 రోజులు. భూమి ద్రవ్యరాశి M_Eని రెండు విభిన్న పద్ధతుల్లో రాబట్టండి.
సాధన:

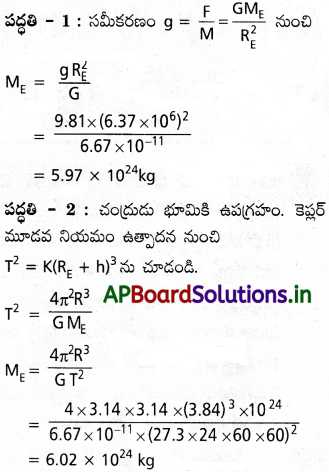
రెండు పద్ధతుల ద్వారా దాదాపు ఒకే ఫలితం వచ్చింది. ఆయా పద్ధతుల ద్వారా వచ్చిన విలువల్లో తేడా 1% కంటే తక్కువగానే ఉంది.

ప్రశ్న 7.
స్థిరాంకం Kని రోజుల్లోను, కిలోమీటర్లలోను వ్యక్తీకరించండి. k = 10^-13s²m^-3 భూమి నుంచి చంద్రునికి ఉన్న దూరం 3.84 ×10⁵ km. చంద్రుని పరిభ్రమణావర్తన కాలాన్ని రోజుల్లో లెక్కించండి.
సాధన:

ఈ K విలువను, సమీకరణం T² = K(R_E + h)³ ని ఉపయోగించి చంద్రుని పరిభ్రమణావర్తన కాలాన్ని లెక్కకట్టవచ్చు.
T² = (1.33 × 10^-14) (3.84 ×10⁵)³
T = 27.3 d
సమీకరణం T² = K(R_E + b)³ లోని (R_E + h) స్థానంలో దీర్ఘవృత్తం అర్థగురు అక్షం పొడవును ప్రతిక్షేపిస్తే, సమీకరణం (9.38) దీర్ఘవృత్తాకార కక్ష్యలకు కూడా వర్తిస్తుంది. అప్పుడు దీర్ఘవృత్తం ఏదోఒక నాభి వద్ద భూమి ఉంటుంది.

ప్రశ్న 8.
400 kg ద్రవ్యరాశి ఉన్న ఒక కృత్రిమ ఉపగ్రహం భూమి చుట్టూ 2R_E వ్యాసార్థం ఉన్న వృత్తాకార కక్ష్యలో పరిభ్రమిస్తుంది. దాన్ని 4R_E వ్యాసార్థం ఉన్న వృత్తాకార కక్ష్యలోకి ప్రవేశపెట్టాలంటే ఎంత శక్తి అవసరమవుతుంది? గతిజశక్తి, స్థితిజశక్తిలో వచ్చే మార్పులు ఏమిటి?
సాధన:

తక్కువ వ్యాసార్థం ఉన్న కక్ష్య నుంచి ఎక్కువ వ్యాసార్థం ఉన్న కక్ష్యకు ఉపగ్రహం బదిలీ అయితే, గతిజ శక్తి తగ్గుతుంది. అది ∆Eని అనుకరిస్తుంది. ఎలా అంటే,
∆K = K_f – K_i;
= -3.13 × 10⁹ J
ఇదే సందర్భంలో స్థితిజ శక్తిలోని మార్పు మొత్తం శక్తిలోని మార్పుకు రెండు రెట్లు ఉంటుంది. ఎలా అంటే,
∆V = V_f – V_i
= – 6.25 ×10⁹ J