Students get through AP Inter 2nd Year Chemistry Important Questions Lesson 3(b) Chemical Kinetics which are most likely to be asked in the exam.
AP Inter 2nd Year Chemistry Important Questions Lesson 3(b) Chemical Kinetics
Very Short Answer Questions
Question 1.
What is Rate of a reaction ?
Solution:
Rate of reaction : The rate [speed or velocity] of a reaction is the change in concentration of reactants or products per unit time.
Rate = \(\frac{\Delta x}{\Delta t}\) Where, Δx is the change in concentration, At is the time interval.
The rate of reaction is always positive and it decreases as the reaction proceeds.
For the reaction, R → P, rate may be expressed as

Question 2.
What is Rate equation (or) Rate expression (or) Rate Law ?
Answer:
Rate equation or Rate expression or Rate Law is the mathematical expression in which aA + bB → cC + dD reaction rate is given in terms of molar concentration of reactants. Where a, b, e and d are the stoichiometric coefficients of reactants and products.
The rate expression for this reaction is Rate ∝ [A]x [B]y
Exponents x and y may or may not equal to stiochiometric coefficients a and b.
Rate = K [A]x [B]y Where K is proportionality constant called rate constant.
![]()
Question 3.
Write the differences between Order and Molecularity of a reaction. (IPE 2014, BIE) (A.P. Mar. ’18)
Solution:
Differences between Order and Molecularity of a reaction :
Order of reaction
- Order is the sum of powers of concentration terms of reactants in the rate law.
aA + bB → cC + dD Rate = K [A]x [B]y
x + y is the total order of the reaction. x and y may or may not be equal to a and b respectively.
Ex : 2H2O2 → 2H2O + O2 is an example for first order reaction. - It is determined by experiment.
- It may be zero, positive, fractional 0, 1, 2, 1.5 etc.,
Molecularity of reaction
i) Molecularity is the no. of reacting species taking part in an elementary reaction.
Ex:
i) NH4NO2 → N2 + 2H2O
(Unimolecular)
Ex : ii) 2HI → H2 + I2 (Bimolecular)
Ex: iii) 2NO + O2 → 2NO2 (Trimolecular)
ii) It is determined by reaction mechanism.
iii) It cant be zero, fractional or negative. It is always a whole number.
![]()
Question 4.
The rate constant of a first order reaction (K) is 5.5 × 10-14 sec-1. Find the half life. (IPE 2015(AP))
Solution:
Half life for a first order reaction is, t1/2 = \(\frac{0.693}{\mathrm{~K}}\)
t1/2 = \(\frac{0.693}{5.5 \times 10^{-14} \mathrm{~S}^{-1}}\) = 1.26 × 1013S
Question 5.
What is Zero Order reaction ?
Solution:
Zero Order reaction: The rate of reaction is independent of the concentration of reactants.
For the reaction R → P, Rate = –\(\frac{\mathrm{d}[\mathrm{R}]}{\mathrm{dt}}\) = k[R]
[R] – Concentration of reactant
K – First order rate constant
Ex:
1) Decomposition of NH3 on hot Pt surface ; ![]()
2) Decomposition of HI on Gold surface is a zero order reaction ![]()
Question 6.
What is First Order reaction ? Give example. (IPE 2014)
Solution:
First Order reaction: The rate of reaction which depends only on one concentration term.
For the reaction R → P, Rate = \(-\frac{d[R]}{d t}\) = k[R]
[R] – Concentration of reactant
K – First order rate constant
Ex:
- Decomposition of N2O5 N2O5 (g) → 2NO2(g) + 1/2 O2 (g)
- Decomposition of N2O N2O(g) → N2(g) + 1/2 O2(g).
Question 7.
What are pseudo first order reactions ? Give one example.
Answer:
First order reactions whose molecularity is more than one are called pseudo first order reactions.
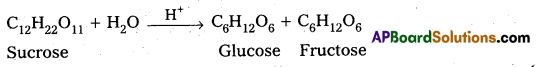
Order = 1
molecularity = 2
Question 8.
What is Half life of a reaction ?
Solution:
Half life of a reaction: The time in which the concentration of a reactant is reduced to one half of its initial concentration is called half life period. It is represented by t1/2.
t1/2 of nth order reaction is given by t1/2 ∝ [R0]1-n
Where R0 is initial concentration
t1/2 = \(\frac{\left[R_{0}\right]}{2 k}\) for a zero order reaction; t1/2 = \(\frac{0.693}{k}\) for first order reaction
![]()
Question 9.
Define the speed or rate of a reaction.
Answer:
The change in the concentration of a réactant (or) product in unit time is called speed or rate of a reaction.
(or)
The decrease in the concentration of a reactant (or) increase in the concentration of product per unit time.
Question 10.
Define Order of a reaction. Illustrate your answer with an example. (IPE 2015; T.S. Mar. ’15)
Answer:
Order of a reaction : The sum of the powers of the concentration terms of the reactants present in the rate equation is called order of a reaction.
- Order of a reaction can be 0, 1, 2, 3 and even a fraction.
Eg:
- N2O5 → N2O4 + \(\frac{1}{2}\)O2
rate ∝ [N2O5]
∴ It is a first order reaction. - 2N2 → 2N2 + O2
rate ∝ [N2O]2
∴ It is 2nd first order reaction.
Question 11.
What are elementary reactions?
Answer:
The reactions taking place in one step are called elementary reactions.
Question 12.
Give two examples for zero Order reactions.
Answer:
Examples for zero order reactions
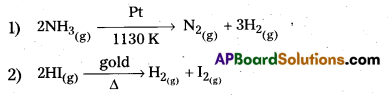
Question 13.
Write the integrated equation for a first order reaction in terms of [R], [R0] and ‘t’.
Answer:
[R] = Concentration of reaction after time T
[R0] = Initial concentrations of reactant
∴ k = \(\frac{2.303}{t}\)log\(\frac{\left[R_0\right]}{[R]}\)
This is the integrated equation for a first order reaction
![]()
Question 14.
Give two examples for gaseous first order reactions.
Answer:
The following are the examples for gaseous first order reactions
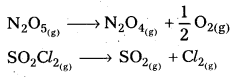
Question 15.
What is a second order reaction? Give one example.
Solution:
Second order reaction : The reactions in which the rate of reaction depends on changing concentration of two substances is called second order reaction.
Ex : Alkaline hydrolysis of ester.
Question 16.
A reaction has a half – life of 10 minutes. Calculate the rate constant for the first order reaction. (IPE 2016 (TS)
Solution:
In case of first order reaction t1/2 = \(\frac{0.693}{k}\)
∴ k = \(\frac{0.693}{\mathrm{t}_{1 / 2}}\) = \(\frac{0.693}{10}\) = 0.0693 min-1
Question 17.
In a first order reaction, the concentration of the reactant is reduced from 0.6 mol/L to 0.2 mol/L in 5 min. Calculate the rate constant (k).
Solution:
a = 0.6mol L-1; a – x = 0.2 mol L-1; t = 5 min.
Since it is a first order reaction.
k = \(\frac{2.303}{\mathrm{t}}\) log10 \(\frac{a}{(a-x)}\)
k = \(\frac{2.303}{t}\) log \(\frac{0.6}{0.2}\) = 0.2197 min-1
Short Answer Questions
Question 1.
Define and explain the order of a reaction. How is it obtained experimentally ?
Answer:
Order of a reaction : The sum of the powers of the concentration terms of the reactants present in the rate equation is called order of a reaction.
- Order of a reaction can be 0, 1, 2, 3, and even a fraction.
Eg:
1) N2O5 → N2O4 + \(\frac{1}{2}\)O2
rate ∝ [N2O5]
∴ It is a first Order reaction.
2) 2N2 → 2N2 + O2
rate ∝ [N2O]2
∴ It is 2nd order reaction
- Order of a reaction can be determined experimentally.
Half-Time (t1/2) method: The time required for the initial concentration (a) of the reactant to become half its value (a/2) during the progress of the reaction is called half-time (t1/2) of the reaction.
A general expression for the half life, (t1/2) is given by
t1/2 ∝ \(\frac{1}{a^{n-1}}\)
Therefore, for a given reaction two halftime values (t’1/2 and t”1/2) with initial concentrations a’ and a” respectively are determined experimentally and the order is established from the equation.
\(\left(\frac{\mathrm{t}_{1 / 2}^{\prime}}{\mathrm{t}_{1 / 2}^{\prime}}\right)\) = \(\left(\frac{a^n}{a^{\prime}}\right)^{n-1}\)
Where ‘n’ is the order of the reaction.
![]()
Question 2.
Describe the salient features of the collision theory of reaction rates of bimolecular reactions.
Answer:
Collision theory of reaction rate bimolecular reactions salient features.
- The reaction molecules are assumed to be hard spheres.
- The reaction is postulated to occur when molecules collide with each other.
- The number of collisions per second per unit volume of the reaction mixture is known as collision frequency (Z).
- For a bimolecular elementary reaction.
A + B → products
Rate = ZAB. e-Ea/RT ; ZAB = collision frequency.
- All collisions do not lead to product formation.
- The collisions with sufficient kinetic energy (Threshold energy) are responsible for product formation. These are called as effective collisions.
- To account for effective collisions a factor p called to probability factor or steric factor is introduced.
Rate = P ZAB. e-Ea/RT
Question 3.
What is “moleculartiy” of a reaction ? How is it different from the ‘order’ of a reaction ? Name one bimolecular and one trimolecular gaseous reactions.
Answer:
The number of reacting species (atoms, ions or molecules) taking parts in an elementary reaction, which must colloid simultaneously to bring about a chemical reaction is called molecularity of a reaction.
NH4NO2 → N2 + 2H2O (Unimolecular)
2HI → H2 + I2 (Bimolecular)
2NO + O2 → 2NO2 (Trimolecular)
- Molecularity has only integer values (1, 2, 3, ….)
- It has non zero, non fraction values while order has zero, 1, 2, 3, ….. and fractional values.
- It is determined by reaction mechanism, order is determined experimentally.
Question 4.
What is half-life (t1/2) of a reaction ? Derive the equations for the ‘half-life’ value of zero and first order reactions.
Answer:
The time required for the initial concentration of the reactants to become half of it’s value during the progress of the reaction is called half life (t1/2) of reaction.
Eg : The radio active of C-14 is exponential with a half life of 5730 years.
Half life of zero order reaction :

![]()
Question 5.
Explain the terms
a) Activation energy (Ea)
b) Collision frequency (Z)
c) Probability factor (P) with respect to Arrhenius equation.
Answer:
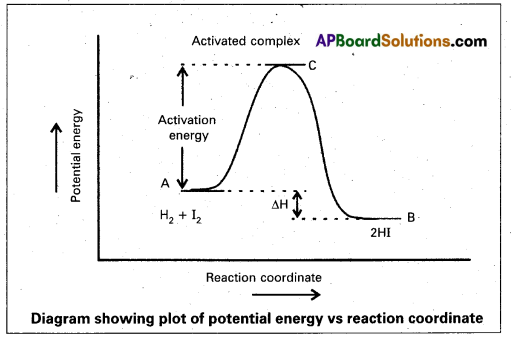
a) Activation Energy: The energy required to form an intermediate called activated complex (C) during a chemical reaction is called activation energy.
b) Collision frequency: The number of collisions per second per unit volume of the reaction mixture is called collision frequency (Z). For a bimolecular elementary reactions
A + B → products
c) Probability factor (P) with respect to Arrhenius equation : To account for effective collisions a factor p called to probability factor or steric factor is introduced.
![]()
Question 6.
Explain the factors influencing rate of reaction. (IPE 2015 (TS))
Solution:
Factors affecting rate of a reaction: The rate of a chemical reaction depends on the following.
i) Concentration of reactants : The rate of a chemical reaction is directly proportional to the concentration of the reactants. As the concentration of reactants increases the number of molecules increase, collisions between molecules increases as a result number of fruitful collisions increases, hence rate of reaction increases.
ii) Nature of reactants : Reactions between ionic compounds are fast when compared to reactions between the covalent compounds. In case of ionic reactions only exchange of ions takes place, hence the reactions between ionic compounds in solutions are very fast. In case of covalent molecules breaking and formation of bonds involved hence the reactions between covalent molecules are very slow.
iii) Temperature : As temperature increases, the rate of reaction increases. For every 10°C rise of temperature the rate of reaction is almost doubled. At high temperatures maximum number of molecules are activated. The collisions between activated molecules are fruitful, hence the rate of reaction increases.
iv) Catalyst: In the presence of catalyst also the rate of reaction increases. Catalyst takes the reaction in a new path having low activation energy.
Question 7.
Show that in the case of first order reaction, the time required for 99.9% completion of the reaction is 10 times that required for 50% completion. (log 2 = 0.3010)
Solution:
Initial concentration, a = 100; Half life period, t1/2 = 0.693/K
Concentration after time ‘t’ = a – x = 100 – 99.9 = 0.1
For first order reaction, K = \(\frac{2.303}{t}\)log\(\frac{a}{(a-x)}\)

![]()
Question 8.
Derive an integrated rate equation for a first order reaction.
Answer:
In first order reactions rate depends on only one concentration term.
R → P
Rate = k[R]; \(\frac{\mathrm{d}[\mathrm{R}]}{\mathrm{dt}}\) = -k. dt
Integration on both sides
ln[R] = -kt + I ——- (1)
I = Integration constant
At t = 0, [R] = [R0] ⇒ ln[R0] = I
Substituting I = ln [R] in the above equation (1)
lñ [R] = -kt + ln[R0]
ln \(\frac{[\mathrm{R}]}{\left[\mathrm{R}_0\right]}\) =-kt . ——— (2)
k = \(\frac{1}{\mathrm{t}} \ln \frac{\left[\mathrm{R}_0\right]}{[\mathrm{R}]}\)
Taking antilog on both sides of eq. (2)
R = [Ro]. e-kt
This is first order rate equation.