AP Inter 2nd Year Maths 2A Important Questions Chapter 2 డిమోయర్ సిద్ధాంతం

Students get through AP Inter 2nd Year Maths 2A Important Questions Chapter 2 డిమోయర్ సిద్ధాంతం which are most likely to be asked in the exam.

AP Inter 2nd Year Maths 2A Important Questions Chapter 2 డిమోయర్ సిద్ధాంతం

ప్రశ్న 1.
\(\frac{(\cos \alpha+i \sin \alpha)^4}{(\sin \beta+i \cos \beta)^8}\) సూక్ష్మీకరించండి.
సాధన:

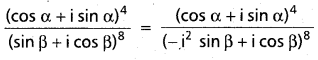
ప్రశ్న 2.
m,n లు పూర్ణాంకాలు, x =cos α +i  sin α, y = cosβ +i sin β అయితే, \(x^m y^n+\frac{1}{x^m y^n}\) = cos (m α+n β)  మరియు \(x^m y^n-\frac{1}{x^m y^n}\) అని చూపండి.
సాధన:

ప్రశ్న 3.
n ధనహూర్గాంకం అయితే, (1+i)ⁿ+(1-i)ⁿ \(2^{\frac{n+2}{2}} \cos \left(\frac{n \pi}{4}\right)\) అని చూపండి.
సాధన:

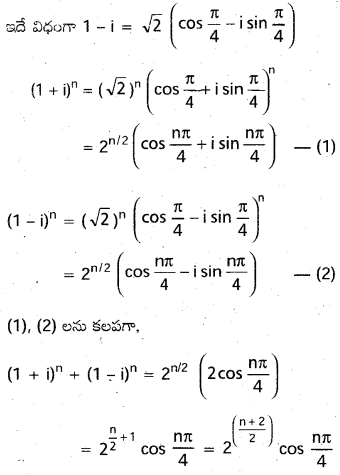
ప్రశ్న 4.
ధనహార్ణాంకం అయితే (1+cos θ +i sin θ)ⁿ +(1+cos θ -i sin θ)ⁿ=2ⁿ⁺¹ \(\cos \left(\frac{n \theta}{2}\right)\) అని చూపండి.
సాధన:

ప్రశ్న 5.
Cos α + Cos β + Cos γ = 0 = sin α + sin β + sin γ అయితే  y cos² α + cos² β + cos² γ = \(\frac{3}{2}\)
sin² α +sin² β + sin² γ అని చూపండి.
సాధన:

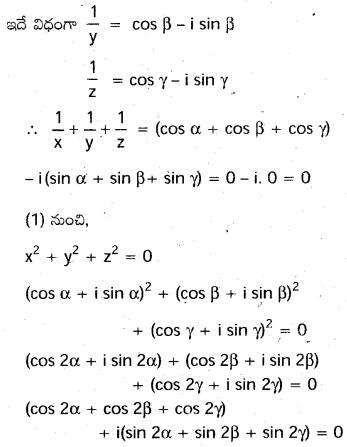
ప్రశ్న 6.
\((\sqrt{3}+i)^{1/4}\) విలువలు కనుక్కోండి.
సాధన:

ప్రశ్న 7.
x¹¹-x⁷+x⁴-1=0 సమీకరణానికి మాలాలు కనుక్కోండి.
సాధన:
x¹¹-x⁷+x⁴-1 = o
= x⁷(x⁴ – 1) + 1(x⁴– 1) = 0
(x⁴ – 1) (x⁷ + 1) = 0
సందర్భం : x⁴ – 1 = 0
x⁴ = 1 = (cos 0 + j sin 0)

ప్రశ్న 8.
ఏకకపు ఘన మూలాలు 1, ω, ω² అయితే,
(i) (1 – ω+ω²)⁶+(1 – ω²+ω)⁶=128= (1 – ω+ω²)⁷ +(1 + ω – ω²)⁷
(ii) (a+b)(aω+bω²)(aω²+bω)=a³+b³
(iii) x=ω-ω²-2 అయితే,  x²+4x+7=0 అని చూపండి.
సాధన:

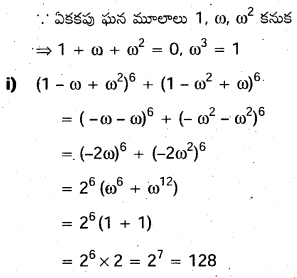
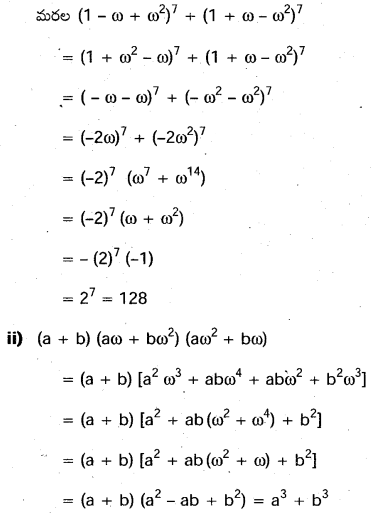
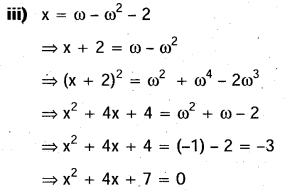
ప్రశ్న 9.
α, β లు x²+x+1=0  కు మూలాలు అయితే α⁴+β⁴+α^-1 β^-1 =0 అని చూపండి.
సాధన:
α, β  x² + x +1 = 0 కు మాలాలు అయతే