AP Inter 2nd Year Maths 2A Important Questions Chapter 3 వర్గసమాసాలు

Students get through AP Inter 2nd Year Maths 2A Important Questions Chapter 3 వర్గసమాసాలు which are most likely to be asked in the exam.

AP Inter 2nd Year Maths 2A Important Questions Chapter 3 వర్గసమాసాలు

ప్రశ్న 1.
ax² + bx + c = 0 వర్గ సమీకరణానికి మూలాలు \(\frac{-b \pm \sqrt{b^2-4 a c}}{2a}\) అని చూపండి.
సాధన:
ax² + bx + c = 0
= 4a(ax² + bx + c) = 0
= 4a²x² + 4abx + b²-b² + 4ac = 0
(2ax + b)² = b² – 4ac

ప్రశ్న 2.
a, b, c ∈ R, a ≠ 0 అనుకొందాం. అప్పుడు R లోని అన్ని x లకు, ax²+b x+c, a లకు ఒకే గుర్తు ఉంటేనే a²+b x+c=0 మాలాలు వాస్తవేతర సంకీర్ణ సంఖ్లావుతాయి.
సాధన:
ax²+b x+c=0 సమీకరణానికి వాస్తవేతర సంకీర్ణ మూలాలు ఉండటానికి నియమం b²-4 a c<0, అంటే 4 ac-b²>0


కాబట్టి 4 ac-b²>0, అందువల్ల b²-4 a c<0. ఈ విధంగా అన్ని వాస్తవ x విలువలకు ax²+bx+c, a లకు ఒకే గుర్తు ఉన్నప్పుడు మాత్రమే b²-4 a c<0 అవుతుంది.

ప్రశ్న 3.
ax²+bx+c=0 సమీకరణానికి సమాన మాలాలు ఉంటే, అపుడు x=\(-\frac{b}{2a}\) తప్ప తక్కిన అన్ని వాస్తవ x విలువలకు ax²+bx+ c, లకు ఉంటుంది అని చూపండి.
సాధన:

ప్రశ్న 4.
α, β లు ax²+bx+c=0 కు వాస్తవ మూలాలు మరియు α<β అయిన
(i) α<β < β అయినపుడు ax²+bx+c=0 లకు వృతరేే గుర్తులా ఉంటాయి.
(ii) x < α లేదా x >β అయినపుడు ax²+bx+ c, లకు ఒకే గుర్తు ఉంటుంది.
సాధన:
α, β లు a x²+b x+c=0 కు మూలాలు కనుక a x²+b x+c=a (x-α) (x-β)

ప్రశ్న 5.
f(x)=a x²+b x+c వర్గ సమాసం.
(i) a>0 అయినపుడు f(x) కు =\(-\frac{b}{2a}\) వద్ద కనిష్ఠ విలువ \(=\frac{4 a c-b^2}{4a}\) అనీ,
(ii) a<0 అయినప్పుడు f(x) కు x= \(-\frac{b}{2a}\) వద్ద గరిష్ఠ విలువ \(=\frac{4 a c-b^2}{4a}\) అని చూపండి.
సాధన:

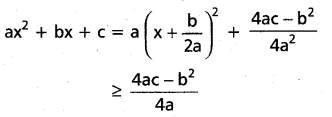
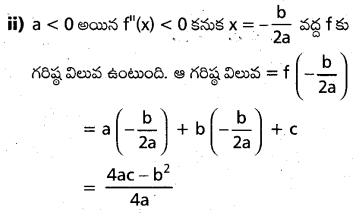
ప్రశ్న 6.
a₁ x²+ b₁ x+c₁=0, a₂ x²+b₂ x+c₂=0 వర్గసమీకరణాలకు ఉమ్మడి మూలం ఉండటానికి ఆవశ్యక, పర్యాప్త నియమాలను నిరూపించుము.
సాధన:
దత్త సమీకరణాల ఉమ్మడి మూలం α అనుకొందాం.
అప్పుడు
a₁α² + b₁α + c₁ 0 — (1)
a₁α² + b₂α + c₂ = 0 — (2)
సమీకరణం (1) ని a₂ తో సమీకరణం (2) ను a₁ తో గుణిస్తే వచ్చిన సమీకరణాలలో రెండోదాన్ని మొదటి దానినుంచి తీసివేస్తే కక్రింది సమీకరణం వస్తుంది.
a₂b₁a – a₁b₂a + a₂c₁  – a₁c₂ = 0
అంటే α (a₂b₁ – a₁b₂) = a₁c₂ –  a₂c₁
అంటే α (a₁b₂ – a₂b₁) = c₁a₂ –  c₂a₁ — (3)
సమీకరణం (1) ని b₂ సమీకరణం (2) ను b₁ తో గుణిస్తే వచ్చిన సమీకరణాలలో రెండోదాన్ని మొదటి దానినుంచి తీసివేస్తే క్రింది సమీకరణం వస్తుంది.
a₂ (a₁b₂ – a,b₁) = b₁c₂ – b₂c₁ — (4)
సమీకరణం (3)ను రెండువైపలా వర్గంచేసి (4) ను ఉపయోగిస్తే పర్యాప్తత
(a₁b₂ – a₂b₁) (b₁c₂ – b₂c₁) = (c₁a₂ – c₂a₁)₂ — (5) అనుకొందాం.

ప్రశ్న 7.
3 x²+2 x-5=0 సమీకరణం మూలాలు కనుక్కోండి.
సాధన:
a x²+b x+c=0 వర్గ సమీకరణం మూలాలు

1,\(-\frac{5}{3}\) లు వర్గ సమాసం 3 x²+2 x-5 క శూన్యాలు అయినందువల్ల, అవి 3 x²+2 x-5=0 సమీకరణానికి మూలాలు.

ప్రశ్న 8.
4 x²-4 x+17=3 x²-10 x-17 సమీకరణం మాలాలు కనుక్కోండి.
సాధన:
దత్తసమీకరణాన్ని x²+6 x+34=0 గా రాయవచ్చు. a x²+b x+c=0 వర్గ సమీకరణం మూలాలు
\(\frac{-b \pm \sqrt{b^2-4 a c}}{2a}\)
ఇక్కడ  a=1, b=6, c=34
అందువల్ల దత్తసమీకరణం మూలాలు

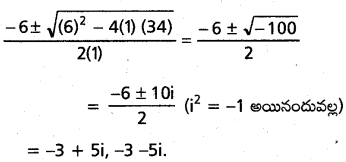
ప్రశ్న 9.
\(\sqrt{3} x^2+10 x-8 \sqrt{3}=0\) కు మాలాలను కనుక్కోండి.
సాధన:
ఇచ్చట a=\(\sqrt{3}\), b=10, c=-8 \(\sqrt{3}\)

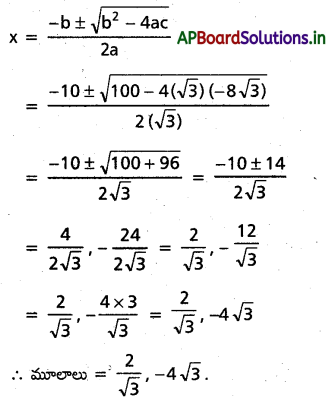
ప్రశ్న 10.
x²-20 x+25=0 సమీకరణం మాలాల స్వభావాన్ని కనుక్కోండి.
సాధన:
ఇచ్చట a = 4, b=-20, c=25
Δ =b²– 4ac
= 400 – 4(4)(25)=0
∴ Δ =0, a, b, c ∈ Q కనుక మూలాలు వాస్తవాలు, సమానములు.

ప్రశ్న 11.
3 x²+7 x+2=0 సమీకరణం మూలాల స్వభావాన్ని తెల్పండి
సాధన:
ఇచ్చట a=3, b=7, c=2
Δ =b²– 4ac
= 49 – 4(3)(2) = 25 = 5² = సంపూర్ణ వర్గం
a, b, c ∈ Q మరియు Δ >0 సంపూర్ణ వర్గం కనుక మూలాలు వాస్తవాలు, విభిన్న అకరణీయ సంఖ్యలు.

ప్రశ్న 12.
x² -2(1+3 m) x+7(3+2 m) = 0 సమీకరణం మూలాలు సమానమైన, m విలావలను కనుగొనుము.
సాధన:
ఇచ్చట a=1, b=-2(1+3 m), c=7(3+2 m) మూలాలు సమానం కనుక Δ = 0
⇒ b – 4ac = 0
⇒ 4(1 + 3m)² – 4(1) (7) (3 + 2m) = 0
⇒ 4{(1 + 3m)² – 7(3 + 2m)} = 0
⇒ 1 + 9m² + 6m-21-14m = 0
⇒ 9m²=8m – 20 =  0
9m² – 18m + 10m-20 = 0
9m(m  – 2) + 10(m – 2) =  0
⇒ (m – 2)(9m+ 10)= 0
⇒  m = 2 లేదా m = \(-\frac{10}{9}\)

ప్రశ్న 13.
α, β లు ax ²+bx+c = 0  కు మాలాలు అయిన α²+β², α³+β³ విలువలు a, b, c లలో కనుగొనుము.
సాధన:

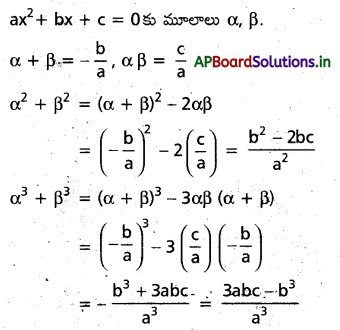
ప్రశ్న 14.
P,Q,R లు అరణీయ సంఖ్లైన, x²  -2px -p²– q²+2 qr – r² = 0 వర్ సమీకరణం మూలాలు అకరోయ సంఖ్యలు అని చూపండి.
సాధన:
ఇచ్చట a=1, b=-2 p, c=p²– q²+2 qr – r²
విచక్షణి (Δ) =b²– 4 ac
= (-2p)² – 4(1)(p²-q²+2 qr – r²
= 4 p²-4p² + 4 q²-8 qr + 4 r²
=4(q-r)²
∵ p, q, r లు అకరణీయ సంఖ్లలు కనుక విచక్షణి అనేది 2(q-r) అకరణీయ సంఖ్య వర్గం.
∴ దత్త సమీకరణం మూలాలు అకరణీయ సంఖ్యలు.

ప్రశ్న 15.
ఈ క్రింది మూలాలుగా గల వర్గ సమీకరణాలను కనుక్కోండి. \(2 \sqrt{3}-5,-2 \sqrt{3}-5\).
సాధన:

ప్రశ్న 16.
మాలాల మొత్తం 1, వాటి వర్గాల మొత్తం 13 గా గల వర్గ సమీకరణాన్ని కనుక్కోండి..
సాధన:
వర్గ సమీకరణానికి మూలాలు α, β లు అనుకుంటే,

ప్రశ్న 17.
α, β ల a x²+b x+c=0 కు మాలాలు c ≠ 0 అయిన \(\frac{1-\alpha}{\alpha}, \frac{1-\beta}{\beta}\) లు మూలాలుగా గల వర్గ సమీకరణాన్ని కనుక్కోండి..
సాధన:

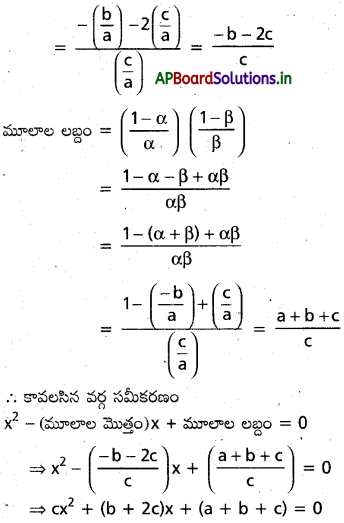
ప్రశ్న 18.
x^2/3+x^2/3-2 = 0 ను సాధించండి
సాధన:
(x^1/3)² + x^1/3 – 2 = 0
x^1/3 = a అనుకుందాం
a² + a – 2 = 0
(a + 2) (a -1) = 0
= a = 1 లేదా a = – 2
= x^1/3 = 1 లేదా x^3/1 = – 2
x = 1 లేదా x = (-2) = – 8
∴ మూలాలు 1,- 8

ప్రశ్న 19.
x వాస్తవం అయిన 7^1+x+7^1-x = 50 ను సాధించుము.
సాధన:

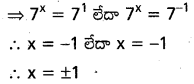
ప్రశ్న 20.
\(\sqrt{\frac{x}{1-x}}+\sqrt{\frac{1-x}{x}}=\frac{13}{6}\)
సాధన:

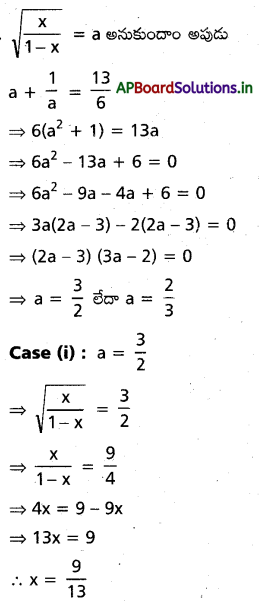
ప్రశ్న 21.
ఒక ధన వాస్తవ సంఖ్ల తన ధనాత్మక మూలానికన్నా 12 ఎక్కువ అయిన ఆ సంఖ్యను కనుక్కోండి.
సాధన:
ధనవాస్తవ సంఖ్య ‘x’ అనుకుందాం.
దత్తాంశం ప్రకారం, x=\(\sqrt{x}+12\) ………….. (1)
=x-12= √x
(x – 12)² = x
= x² – 24x+ 144= x
= x² – 25x+ 144 = 0
= (x – 9) (x – 16) =0
= x = 9 లేదా  16
x = 9 అయిన L.H.S.=9,
R.H.S. = √9- 12 = 15,
LH.S. ≠ R.H.S.
x=16 అయిన L.H.S.=16,
R.H.S. = √16+ 12 = 16,
L.H.S. = R.H.S.
∴ కనుక కావలసిన ధన వాస్తవ సంఖ్య =16

ప్రశ్న 22.
x²+4 a x+3=0,2 x²+3 a x-9=0 సమీకరణాలకు ఉమ్మడి మాలం ఉంటే, అప్పుడు a విలువలను, ఉమ్మడి మాలాన్నీ కనుక్కోండి.
సాధన:

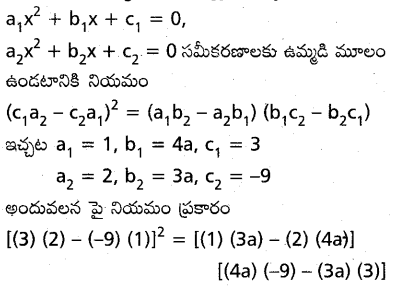
(15)² = (−5a) (−45a)
225 = 225a² ⇒ a² = 1 ⇒ a = ±1
a = 1 అయితే దత్త సమీకరణాలు
x + 4x + 3 = 0,
2x² + 3x – 9 = 0
i.e., (x + 1) (x + 3) = 0;
(2x − 3) (x + 3) = 0
వాటి మూలాలు వరుసగా -1, -3; 3/2, -3
కనుక దత్త సమీకరణాల ఉమ్మడి మూలం -3
ఇట్లే a = -1 అయిన దత్త సమీకరణాలు
x² – 4x + 3 = 0,
2x²-3x – 9 = 0
i.e., (x – 1) (x – 3) = 0,
(2x + 3) (x − 3) = 0
వాటి మూలాలు వరుసగా 1, 3,\(-\frac{3}{2}\), 3
కనుక దత్త సమీకరణాల ఉమ్మడి మూలం 3.
దత్త సమీకరణాల ఉమ్మడి మూలాలు 3, -3 లు.

ప్రశ్న 23.
రెండు వరుస ధనాత్మక బేసి పూర్ణసంఖ్యల వర్గాల మొత్తం 290 అయ్యేటట్లు ఒకే ఒక జత ఉంటుందని చూపి, వాటిని కనుక్కోండి.
సాధన:
రెండు వరుస ధనాత్మక బేసి పూర్ణ సంఖ్యల భేదం = 2
కనుక వరుస బేసి ధన పూర్ణాంకాలు X, X + 2 అనుకుందాం. దత్తాంశం ప్రకారం
(x)² + (x + 2)² = 290
⇒ x² + x² + 4x + 4 = 290
⇒ 2 x 2+4 x -286 = 0
⇒ x ² + 2x – 143 = 0
13x – 11x – 143 = 0
⇒ x(x + 13) − 11(x + 13) = 0
⇒ (x – 11) (x + 13) = 0
⇒ x = 11, x = -13
సమీకరణం (1)ని ధృవీకరించే ఏకైక ధనాత్మక బేసి పూర్ణ సంఖ్య 11.
కనుక 11, 13 అనే ఒకే ఒక జత వరుస బేసి ధనాత్మక పూర్ణాంకాలు ఉంటాయి.

ప్రశ్న 24.
ఒక కేబుల్ తీగ ఖరీదు రూ.35.00 లు. తీగ పొడవు గనక 4 మీటర్లు అదనంగా ఉండి ఉంటే, మీటరు ఖరీదు రూ.1.00 చొప్పున తగ్గి మొత్తం ఖరీదు మారకుండా ఉండేది. అయిన తీగ పొడవెంత?
సాధన:
తీగ పొడవు = ‘l’ మీ అనుకోండి.
మీటరు తీగ వెల = X రూ. అనుకొందాం.
అపుడు lx = 35 ………………. (1)
మరియు (l + 4) (x − 1) = 35
⇒ lx + 4x – 1 – 4 – 35
⇒ 35 + 4x – 1 – 4 = 35
⇒ 4x – 1 = 4
⇒ x = \(\frac{l+4}{4}\)
(1), (2) ల నుండి, \(l\left[\frac{l+4}{4}\right]=35\) ………………… (2)
⇒ l² + 4l = 140
⇒ l²+4l-140 = 0
⇒ (l+14) (l-10)= 0
⇒ l= 10 లేదా ! = -14
l ఎల్లప్పుడూ ధనాత్మక సంఖ్య కనుక l = 10 .
∴ కేబుల్ తీగ పొడవు (l) = 10 మీ.

ప్రశ్న 25.
మేకల మందలో నాలగోవంతు అడవిలో మేస్తున్నాయి. మందలోని మేకల సంఖ్య య్తొక్క వర్గమూలానికి రెండు రెట్ల్ల కొండమీదికెళ్ళాయి. విగిలిన 15 మేకలా నది గట్టున ఉన్నాయి. మేకల మొత్తం సంఖ్యను కనుక్కోండి.
సాధన:
మందలోని మేకల సంఖ్య ‘x’ అనుకుందాం.
అపుడు అడవిలో మేస్తున్న మేకల సంఖ్య \(=\frac{\mathrm{x}}{4}\)
కొండ మీదకెళ్ళిన మేకల సంఖ్య \(=2 \sqrt{\mathrm{x}}\)
నది గట్టున ఉన్న మేకల సంఖ్య =15

ప్రశ్న 26.
క్రికెట్టు ఆటలో రవి తీసుకొన్న వికెట్ల సంఖ్యకు రెండు రెట్లు కంటే ఒక వికెట్ తక్కువ అనిల్ తీసుకొన్నాడు. వారిద్దరూ తీసుకొన్న వికెట్ల సంఖ్య లబ్దం 15 అయిన ఒక్కొక్కరూ ఎన్ని వికెట్లు తీసుకొన్నదీ కనుక్కోండి.
సాధన:
రవి తీసుకొన్న వికెట్ల సంఖ్య అనుకుందాం.
అపుడు అనిల్ తీసుకొన్న వికెట్ల సంఖ్య =2 x-1
దత్తాంశం (ప్రకారం (x) (2 x-1)=15
=2x² – x-15 = 0
2x² – 6x + 5x -15 = 0
=2x(x – 3) + 5(x -3) = 0
=(x – 3)(2x + 5) = 0
= x = 3 లేదా – \(\frac{5}{2}\)
x≠ – \(\frac{5}{2}\)
∴ రవి తీసుకొన్న వికెట్ల సంఖ్య (x)=3
అనిల్ తీసుకొన్న వికెట్ల సంఖ్య 2x – 1=6-1=5

ప్రశ్న 27.
సమతలం మీద కొన్ని బిందువులను గుర్తించి, బిందు యుగ్మాలను రేఖాఖండాలతో కలపటం జరిగింది. ఇట్లు చేయగా ఏర్పడిన రేఖా ఖండాల సంఖ్య మొత్తం 10 అయితే, తలం మీద గుర్తించిన ఐిందువుల సంఖ్యను కనుక్కోండి.
సాధన:
తలం పై బిందువుల సంఖ్య = x అనుకోండి.
రెండేసి ఏిందువులను కలిపితే ఏర్పడే రేఖా ఖండాల సంఖ్య

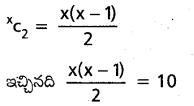
x²-x=20
x² -x-20=0
⇒ (x-5)(x+4)=0
⇒ x =-4,5
x>0 ⇒  x=5
∴ కనీస బిందువుల సంఖ్ = 5

ప్రశ్న 28.
ax²+b x+c=0, bx²+c x+a=0 వర్గ సమీకరణాలకు ఉమ్మడి మూలం ఉంటీ, a³+b³+ c³= 3abc అని చూపండి.
సాధన.
ఉమ్మడి మూలం ‘α’ అనుకోండి. అపుడు
aα ²+bα+c=0
bα²+c α +a=0
అడ్డ గుణకార పద్ధతి ప్రకారం

ప్రశ్న 29.
x యొక్క ఏ  వాస్తవ విలువలకు x²-5 x-14 వర్గ సమాసం ధనాత్మకం అవుతుంది ?
సాధన:
x²-5 x-14 >0
=x² -7x + 2x – 14 = O
x(x – 7) + 2 (x – 7) > 0
=(x + 2)(x -7) >0
= x² గుణకం = 1 >0, x²– 5x- 14 >0
x విలువ (-2,7) ల మధ్య ఉండదు.
⇒ X∈ ( – ∞ , – 2) ∩ (7,∞)

ప్రశ్న 30.
ఏయే x విలువలకు -6x²+2 x-3 ఖిణాత్మకం అవుతుంది ?
సాధన:
-6 x²+2 x-3<0 ⇒ 6 x²-2 x+3>0
ఇచ్టట a=6, b=-2, c=3.
Δ = b²-4 ac = 4 – 4 (6) (3)
= 4 – 72 = – 68 < 0
∵ Δ < 0, x² గుణకం = 6,
కనుక ∀ x ∈ R, 6x²+2x+3>0
లేదా ∀ x ∈ R,- 6x²+2x+3<0

ప్రశ్న 31.
x యొక్క ఏ విలువకు ఈ క్రింది సమాసాలు గరిష్హ లేదా కనిష్ట విలువలు కల్గివంటాయి.

(i) x²+5 x+6
సాధన:
ఇచ్చట a=1, b=5, c=6
∵  a>0, x²+5 x+6 కు x= \(\frac{-b}{2a}\) వద్ద
కనిష్ఠ విలువ ఉంటుంది.
∴ \(x=\frac{-5}{2(1)}=\frac{-5}{2}\)

(ii) 2 x-x²+7
సాధన:
-x²+2 x+7 ఇచ్చట a=-1, b=2, c=7
∵ a<0,-x²+2 +7 కు x = \(\frac{-{b}}{2 {a}}\) వద్ద
గరిష్ఠ విలువ ఉంటుంది.
∴ x = \(-\frac{(2)}{2(-1)}\)=1

ప్రశ్న 32.
ఈ క్రింది వర్గ సమాసాలకు గిిష్ఠ లేదా కనిష్ఠ విలువలను కనుక్రోండి.
(i) 2x-7-5x²
(ii) 3x²+ 2 +11
సాధన:
(i) f(x)=2 x-7-5x² = -5x²+2 x-7
a x²+b x+c తో పోల్చగా
a = -5, b = 2, c = -7

ప్రశ్న 33.
x యొక్క అన్ని వాస్తవ విలువలకు 4 x-5 x²+2 గుర్తులలో మార్పలలను కనుక్కోండి. వాటి అంత్య విలువలను కనుక్కోండి.
సాధన:
సమీకరణం 4 x-5 x²+2=0
⇒ 5 x²-4x-2=0

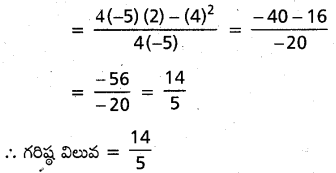
ప్రశ్న 34.
x²+x-12 ≤ 0 యొక్క సాధన సమితిని బీజీయ పద్ధతి, గేఖాచిత్త పద్ధతుల ద్వారా కనుక్కోండి.
సాధన:
బీజీయ పద్ధతి : x²+x-12=(x+4)(x-3).
కాబట్టి x²+x-12=0 సమీకరణం -4, 3.
x²+x -12=0 వర్గ సమాసంలో x² గుణకం ధనాత్మకం
అయినందువల్ల -4<x<3 అయితే x²+ x – 12 రుణాత్మకం, x<-4 గానీ x>3 గానీ అయితే x²+x-12 ధనాత్మకం.
కాబట్టి x²+ x – 12 ≤ 0 ⇔ – 4 ≤ x ≤ 3
అందువల్ల సాధన సమితి {x ∈ R : – 4 ≤ x ≤ 3}.
రేఖా చిత్ర పద్ధతి : y=f(x)=x²+x-12 అనుకొందాం.
x యొక్క కొన్ని ఎంపిక చేసిన విలువలకు y విలువలను క్రింది పట్టికలో ఇచ్చాం.

పట్టికలోని విలువలను ఉపయోగించి y=f(x) రేఖా
చి(తాన్ని గీశాం. దీన్ని పటం 3.4లో  చూపించాం.

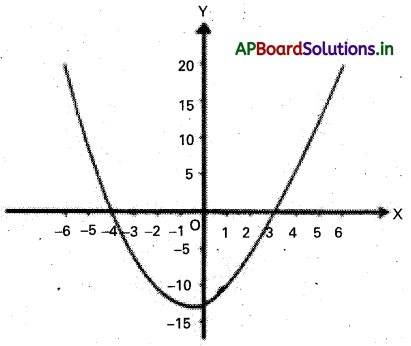
y=f(x) రేఖా y=f(x) రేఖా చిత్రo నుండి -4 ≤ x ≤ 3 అయితేనే y= x²– x -12<0 అవుతుందని మనం గమనిస్తాం. అందువల్ల సాధన సమితి {x ∈ R : – 4 ≤ x ≤3}.

ప్రశ్న 35.
ఏయే x విలువలకు x²-3 x-10<0, 10x – x² – 16 > 0 అసమీకరణాలు రెండు వర్తిస్తామో కనుక్కోండి.
సాధన:
x²-3 x-10<0
x²-5 x+2 x-10<0
x(x-5)+2(x-5)<0
(x-5)(x+2)<0
x ∈ (-2,5) …………… (1)
10 x – x²-16>0
x²-10 x+16<0
x²-8 x-2 x+16<0
x(x-8)-2(x-8)<0
(x-8)(x-2)<0
⇒ x ∈ (2,8) …………… (2)
(1), (2) ల నుండి ఉమ్మడి సాధన 2<x<5

ప్రశ్న 36.
\(\sqrt{\mathbf{x}+2}>\sqrt{8-\mathbf{x}^2}\) అసమీకరణాన్ని సాధించండి.
సాధన:

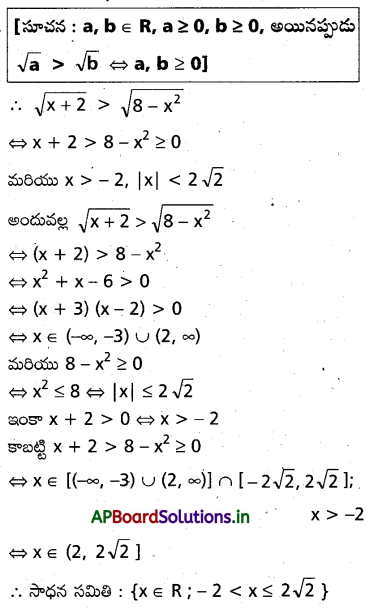
ప్రశ్న 37.
\(\sqrt{(x-3)(2-x)}<\sqrt{4 x^2+12 x+11}\) అసమీకరణాన్ని సాధించండి.
సాధన:
దత్త అసమీకరణం. ఈ (క్రంది రెండు అసమీకరణాలను ఇస్తుంది.

ప్రశ్న 38.
\(\sqrt{\frac{6+x-x^2}{2 x+5}} \geq \sqrt{\frac{6+x-x^2}{x+4}}\) అసమీకరణాన్ని సాధించండి.
సాధన:

ప్రశ్న 39.
\(\sqrt{x^2-3 x-10}>8-x\) అసమీకరణాన్ని సాధించండి.
సాధన:

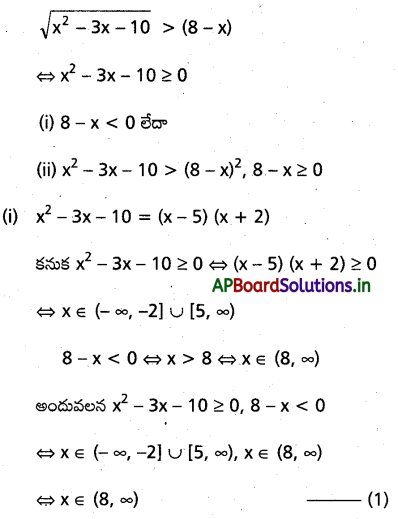
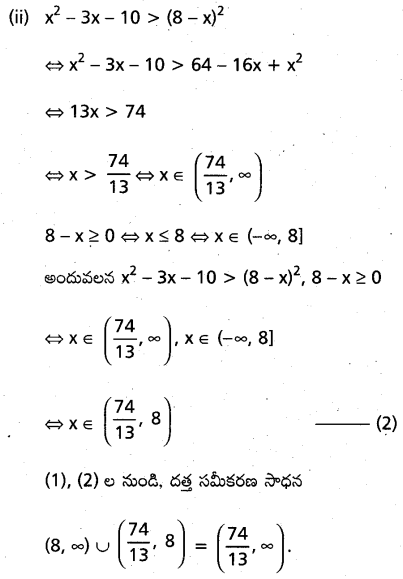
ప్రశ్న 40.
R మీద \(\frac{x^2+14 x+9}{x^2+2 x+3}\) ప్రమేయం గరిష్ఠ విలువను  కనుగొనుము.
సాధన:

ప్రశ్న 41.
R మీద \(\frac{x^2+34 x-71}{x^2+2 x-7}\) మొక్క ఏ విలువలూ 5, 9ల మధ్య ఉండవని చూపండి.
సాధన: