AP Inter 1st Year Physics Study Material Chapter 11 ప్రవాహుల యాంత్రిక ధర్మాలు

Andhra Pradesh BIEAP AP Inter 1st Year Physics Study Material 11th Lesson ప్రవాహుల యాంత్రిక ధర్మాలు Textbook Questions and Answers.

AP Inter 1st Year Physics Study Material 11th Lesson ప్రవాహుల యాంత్రిక ధర్మాలు

అతిస్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
సగటు పీడనాన్ని నిర్వచించండి. దీని ప్రమాణం, మితీయ ఫార్ములాను తెలపండి. ఇది సదిశరాశా? అదిశరాశా?
జవాబు:
సగటు పీడనం (P_av) :
ప్రమాణ వైశాల్యంపై పనిచేసే అభిలంబ బలాన్ని సగటు పీడనం అంటారు.
P_av = \(\frac{F}{A}\)
ప్రమాణాలు → N/m² (లేదా) పాస్కల్
మితిసూత్రం → [ML^-1T^-2]
పీడనం అదిశరాశి.

ప్రశ్న 2.
స్నిగ్ధతను నిర్వచించండి. స్నిగ్ధతా గుణకం ప్రమాణాలు, మితులు ఏమిటి?
జవాబు:
స్నిగ్ధత :
ప్రవాహి రెండు పొరల మధ్య సాపేక్ష వేగాన్ని తగ్గించే ధర్మాన్ని స్నిగ్ధత అంటారు.
C.G.S ప్రమాణాలు పాయిజ్ (Poise)
S.I ప్రమాణాలు → Nm^-2s
మితిసూత్రం →[M¹L^-1T^-1]

ప్రశ్న 3.
ఒక ఆటోమొబైల్ యొక్క కార్బ్యురేటర్ పనిచేయడం వెనక ఉన్న సూత్రం ఏది? [May ’13]
జవాబు:
ఆటోమొబైల్లో ఉండే కార్బ్యురేటర్కు ఒక వెంటురి ఛానెల్ (నాజిల్) ఉంటుంది. దాని ద్వారా ఒక అధిక వడితో గాలి ప్రవహిస్తుంది. గాలి పీడనం ఇరుకైన మెడవద్ద తగ్గడం వల్ల పెట్రోలు పేటికలోకి పీల్చబడుతుంది. ఇలా దహనానికి అవసరమయ్యే గాలి, ఇంధనాల మిశ్రమం సమకూరుతుంది.

ప్రశ్న 4.
మాగ్నస్ ప్రభావం అంటే ఏమిటి?
జవాబు:
స్పిన్ గమనంలో ఉన్న బంతిపైన మరియు క్రింద తలాలపై గాలివేగాలలో తేడా వలన పీడనాలలో కూడా తేడా ఏర్పడి బంతిపై నికర ఊర్థ్వబలం పనిచేస్తుంది. స్పిన్ గమనం వల్ల కలిగే ఈ గతిక ఉత్థాపనాన్నే మాగ్నస్ ప్రభావం అంటారు.

ప్రశ్న 5.
ద్రవ బిందువులు, బుడగలు గోళాకారంలో ఎందుకు ఉంటాయి? [Mar. ’14; May ’13]
జవాబు:
తలతన్యత వల్ల ద్రవతలాలు కనిష్ఠ ఉపరితల వైశాల్యాలను పొందుతాయి. గోళం యొక్క ఉపరితల వైశాల్యం తక్కువ కాబట్టి, వర్షపు చినుకులు గోళాకారంగా ఉంటాయి.

ప్రశ్న 6.
ద్రవ బిందువులోని అదనపు పీడనానికి సమీకరణాన్ని తెలపండి.
జవాబు:
ద్రవబిందువు లోపల అధిక పీడనం, P_i – P_o = \(\frac{2s}{r}\)
ఇక్కడ s = తలతన్యత
r = ద్రవబిందువు వ్యాసార్థం

ప్రశ్న 7.
ద్రవంలోపల ఉండే గాలి బుడగలోని అదనపు పీడనానికి సమీకరణాన్ని తెలపండి.
జవాబు:
ద్రవంలోపల ద్రవపు బిందువులో అధికపీడనం, P_i – P_o = \(\frac{2s}{r}\)
ఇక్కడ s = తలతన్యత
r = గాలిబుడగ వ్యాసార్థం
గాలిబుడగ ద్రవంలోపల ఉంది కాబట్టి, దానిలో ఒక ద్రవతలం మాత్రమే ఉంటుంది.

ప్రశ్న 8.
గాలిలో ఉన్న సబ్బుబుడగలోని అదనపు పీడనానికి సమీకరణాన్ని తెలపండి.
జవాబు:
గాలిలో సబ్బు బుడగకు రెండు తలాలు ఉంటాయి. కాబట్టి సబ్బు బుడగ
లోపల అధికపీడనం, P_i – P_o = \(\frac{4s}{r}\)
ఇక్కడ s = తలతన్యత
r = సబ్బు బుడగ వ్యాసార్థం

ప్రశ్న 9.
జలసంసక్తకాలు (water wetting agents), జలఅసక్తకాలు (water proofing agents) అంటే ఏమిటి? అవి ఏమిచేస్తాయి?
జవాబు:
నీరు, ఫైబర్ల మధ్య ఉండే స్పర్శకోణాన్ని పెంచేందుకై ద్రవాలకు జలజితద్రవ్యాలను (water proofing agents) కలుపుతారు.

సబ్బులు, డిటర్జెంట్లు, రంగులద్దే ద్రవ్యాలు ఇవన్నీకూడా జల సంసక్తకాలు (wetting agents) . వీటిని ద్రవానికి కలిపినప్పుడు స్పర్శకోణం తక్కువై అవి ద్రవంలోకి తేలిగ్గా చొచ్చుకొనిపోయి ప్రభావవంతం అవుతాయి.

ప్రశ్న 10.
స్పర్శకోణం అంటే ఏమిటి?
జవాబు:
ఘనతలం, ద్రవము కలిసే బిందువు వద్ద ద్రవ అంతర్భాగంలో ద్రవతలానికి గీసిన స్పర్శరేఖకు, ద్రవంలో ఘనతలానికి మధ్యగల కోణమును స్పర్శకోణము (9) అంటారు.

ప్రశ్న 11.
బెర్నౌలీ సిద్ధాంతాన్ని పాటించే వాటికి రెండు ఉదాహరణలను ఇవ్వండి. ఆయా ఉదాహరణలను సమర్ధించండి.
జవాబు:
1) బలమైన గాలులు వీచినప్పుడు, ఇంటి పై కప్పులు ఎగిరిపోతాయి. గాలివేగం ఇంటి కప్పుపై భాగంలో ఇంటి లోపలి కన్నా ఎక్కువ. అందువల్ల ఇంటి కప్పు పైన పీడనం తక్కువ. ఇంటిలోపల పీడనం ఎక్కువ. ఈ పీడనాలలో తేడా వల్ల గతిక’ ఉత్థాపన కలుగుతుంది.

2) ఫ్యాన్ తిరుగుచున్నప్పుడు, బల్లపై కాగితాలు ఎగిరిపోతాయి. కాగితంపై భాగంలో గాలివేగం పెరుగుతుంది. అందువల్ల పీడనం తగ్గుతుంది. ఈ పీడనాలలో తేడావల్ల కాగితంపైకి ఎగురుతుంది.

ప్రశ్న 12.
ఒక గొట్టం ద్వారా నీరు ప్రవహిస్తున్నప్పుడు ఆ నీటి ప్రవాహంలో ఏ పొర అత్యధిక వేగంతో ప్రవహిస్తుంది? ఏ పొర అత్యల్ప వేగంతో ప్రవహిస్తుంది?
జవాబు:

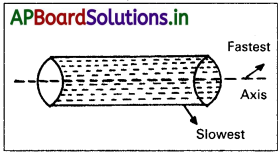
గొట్టం గుండా నీరు ప్రవహిస్తున్నప్పుడు, అక్షానికి దగ్గరగా ఉన్న పొరలో వేగం అధికంగాను, గొట్టం గోడల వద్ద వేగం నెమ్మదిగాను ఉంటుంది.

ప్రశ్న 13.
ఒక వస్తువు యొక్క ఉపరితల వైశాల్యం ఎక్కువైనప్పుడు దాని చరమవేగం (Terminal velocity) కూడా అధికంగా ఉంటుంది. మీ సమాధానాన్ని సమర్ధించే కారణాలను తెలపండి.
జవాబు:
ఉపరితల వైశాల్యం (A) = 4πr²
మరియు చరమవేగం (υ_t) α r²
ఉపరితల వైశాల్యం పెరిగితే, r² కూడా పెరుగుతుంది. అందువల్ల చరమవేగం కూడా పెరుగుతుంది.
∴ ఉపరితల వైశాల్యం పెరిగితే, చరమవేగం కూడా అధికం.

స్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
వాతావరణ పీడనం అంటే ఏమిటి ? భారమితి (బారో మీటర్) సహాయంతో దీన్ని ఎలా నిర్ధారిస్తారు?
జవాబు:
వాతావరణ పీడనం :
ఏదైనా ఒక బిందువు వద్ద వాతావరణ పీడనం, ఆ బిందువు నుండి విస్తరిస్తూ వాతావరణపు పై అంచుదాకా కొనసాగే ఏకాంక మధ్యచ్ఛేద వైశాల్యం గల వాయుస్తంభం యొక్క బరువుకు సమానం.
వాతావరణ పీడనం (1 atm): 1.013 × 10⁵ pa

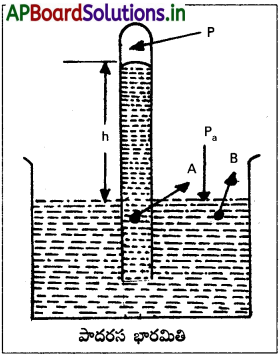
భారమితి ద్వారా వాతావరణ పీడనాన్ని కనుగొనుట :
ఒక కొనవైపు మూసి ఉన్నటువంటి ఒక గాజు గొట్టంలో పాదరసాన్ని నింపి, దానిని ఒక పాదరసం తొట్టిలో పటంలో చూపిన విధంగా బోర్లిస్తారు. ఈ పరికరాన్నే పాదరస భారమితి అంటారు. గొట్టంలో నిలిచిన పాదరస స్తంభం ఎగువన ఉన్న ప్రదేశంలో ఉండేదల్లా పాదరస బాష్పం మాత్రమే. దీని పీడనం ఎంత అల్పంగా ఉంటుందంటే, దాన్ని మనం ఉపేక్షించవచ్చు.
స్తంభం లోపల ఒక బిందువు A వద్ద ఉన్న పీడనం, అదే మట్టం వద్ద ఉన్న బిందువు B వద్ద ఉండే పీడనంతో సమానం అయి తీరుతుంది.

∴ B బిందువు వద్ద పీడనం వాతావరణ పీడనం = P_a

P_a = ρgh = A బిందువు వద్ద పీడనం
ρ అనునది పాదరస సాంద్రత, h అనునది గొట్టంలోని పాదరస స్తంభం ఎత్తు.

బారోమీటరులో పాదరస స్తంభం ఎత్తు సముద్ర మట్టం వద్ద 76cm ఉంటుందని ఈ ప్రయోగం ద్వారా కనుక్కొన్నారు. ఈ ఎత్తు ఒక అట్మాస్ఫియర్ (1 atm) కు తుల్యమైంది.

ప్రశ్న 2.
గేజ్ పీడనం అంటే ఏమిటి ? మానోమీటర్ సహాయంతో పీడన వ్యత్యాసాన్ని ఎలా కనుక్కొంటారు?
జవాబు:
గేజ్ పీడనం :
నిజ పీడనానికి మరియు వాతావరణ పీడనానికి గల తేడాను గేజ్ పీడనం అంటారు.

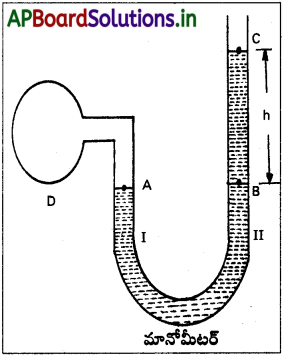
పీడనంలో తేడాలను కొలుచుట :

1. మానోమీటరులోని U- గొట్టంలో తక్కువ పీడన తేడాలు కొలవడానికి అల్ప సాంద్రతగల ద్రవాన్ని (నూనె) మరియు అధిక పీడన తేడాలు కొలవడానికి అధిక సాంద్రత గల ద్రవాన్ని నింపాలి.
2. గొట్టం ఒక కొనకు గాలిపీడనం కొలవవలసిన పాత్ర D ను కలపాలి. మరియు రెండు కొన తెరచి ఉంచాలి.
3. D పాత్రలో భూమి వాతావరణ పీడనం కన్నా గాలి పీడనం అధికంగా ఉంటే భుజం I వైపు ద్రవమట్టం 4 బిందువు కన్నా క్రిందకు ఉంటుంది. భుజం II లో C బిందువు కన్నా పైకి ఉంటుంది.
4. పాత్రలో పీడనం, A బిందువు వద్ద పీడనానికి సమానం.
5. U- గొట్టంలోని రెండు భుజాలలో ద్రవమట్టాలలో తేడాలను గుర్తించాలి. (h అనుకొనుము). ρ అనునది ద్రవం యొక్క సాంద్రత. P_a అనునది వాతావరణ పీడనం.
6. A బిందువు వద్ద పీడనం (P_A) =B బిందువు వద్ద పీడనం = C బిందువు వద్ద పీడనం + ద్రవ స్థంభం యొక్క పీడనం
   P_A = P_C + hρg (లేదా) P_A – P_C = hρg
   ఇక్కడ P_C = P_a P_A = P
   ∴ P – P = hρg
   P – P_a = P_g = పీడన కొలత = hρg

ప్రశ్న 3.
పాస్కల్ నియమాన్ని తెలిపి ఒక ప్రయోగం సహాయంతో దాన్ని నిరూపించండి.
జవాబు:
పాస్కల్ నియమం :
ఈ నియమం ప్రకారం, గురుత్వాకర్షణ ప్రభావంను విస్మరిస్తే, సమతాస్థితిలో నిశ్చలంగా ఉన్నప్పుడు ద్రవం యొక్క ప్రతిబిందువుపై పీడనం ఒకేవిధంగా ఉంటుంది.

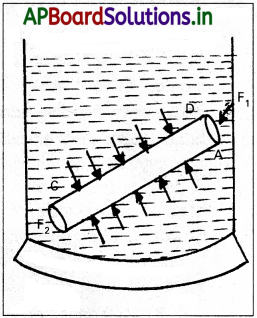
నిరూపణ :

1. ఏకరీతి అడ్డుకోత వైశాల్యం A కల ఒక వృత్తాకార స్థూపాన్ని ఊహించండి మరియు C, D బిందువులు ఆ స్థూపంపై ఉన్నాయనుకొనుము.
2. స్థూపం వెలుపలి వైపు ద్రవం కలిగించే బలాల వల్ల స్థూపంలోపల ద్రవం సమతాస్థితిలో ఉంటుంది.
3. ఈ బలాలు స్థూపం యొక్క తలంపై లంబంగా పనిచేస్తాయి.
4. అందువలన Cమరియు D బిందువుల వద్ద స్థూపం యొక్క చదునుతలాలపై పనిచేసే బలం, స్థూపం యొక్క వక్రతలంపై పనిచేసే బలానికి లంబంగా ఉంటుంది.
5. ద్రవం సమతాస్థితిలో వున్నప్పుడు, స్థూపం యొక్క వక్రతలంపై పనిచేసే బలాల మొత్తం శూన్యం.
6. P₁ మరియు P₂ లు C మరియు D బిందువుల వద్ద పీడనాలు. F₁ మరియు F₂ లు ద్రవం వలన స్థూపం యొక్క చదును తలాలపై పనిచేసే బలాలు అయిన
   F₁ = P₁ A మరియు F₂ = P₂A ద్రవం సమతాస్థితిలో ఉంది కాబట్టి
   F₁ = F₂
   P₁ A = P₂A (లేదా) P₁ = P₂

దీనర్థం C మరియు D బిందువుల వద్ద పీడనాలు ఒకే విధంగా ఉన్నాయి. ఇది పాస్కల్ నియమాన్ని ఋజువు చేస్తుంది.

ప్రశ్న 4.
హైడ్రాలిక్ లిఫ్ట్, హైడ్రాలిక్ బ్రేక్లను వివరించండి.
జవాబు:
హైడ్రాలిక్ లిఫ్ట్ మరియు హైడ్రాలిక్ బ్రేకులు పాస్కల్ నియమంపై ఆధారపడి పనిచేస్తాయి.

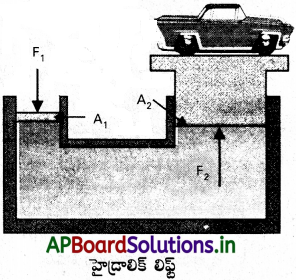
హైడ్రాలిక్ లిఫ్ట్ :
ఇక్కడ వేరు వేరు వైశాల్యాలు గల మరియు D అను రెండు స్థూపాలు ఉంటాయి. వాటిని E గొట్టం ద్వారా కలుపుతారు. ప్రతి స్థూపం ఘర్షణ లేని గాలిబంధిత ముషలకాన్ని కలిగి ఉంటుంది. a మరియు A అనునవి C మరియు D వద్ద ముషలకం అడ్డుకోత వైశాల్యాలు అనుకొనుము (a <<A). ఈ స్థూపాలలో అసంపీడ్య ద్రవాన్ని నింపాలి. f అనునది C వద్ద కలిగించే బలం. ద్రవంపై కలిగే పీడనం P = \(\frac{f}{a}\) …………. (1)
పాస్కల్ నియమం ప్రకారం, ఈ పీడనం D స్థూపంలోని ముషలకానికి ప్రసరిస్తుంది. D వద్ద ఊర్థ్వబలం
F = PA = \(\frac{f}{a}\)A = f\(\frac{A}{a}\) ………….. (2)
A >> a కాబట్టి, F > > f

కాబట్టి పెద్ద స్థూపంపై ఉంచిన పెద్ద బరువులను తేలికగా లేపవచ్చు.

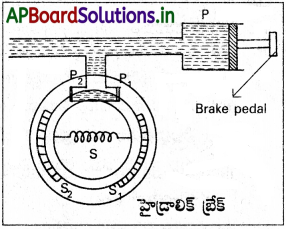
హైడ్రాలిక్ బ్రేకులు :
బ్రేక్ ఫెడల్పై మనం స్వల్ప బలాన్ని ప్రయోగిస్తే, మాస్టర్ స్థూపంలోని ముషలకం కదులుతుంది. P వద్ద ద్రవంపై పీడనం పెరుగుతుంది. పాస్కల్ నియమం ప్రకారం P₁ మరియు P₂ స్థూపాలకు పీడనం సమానంగా ప్రసరిస్తుంది. ఈ కారణం చేత P₁ మరియు P₂ బయటకు జరిగి, బ్రేక్ షూలు వ్యాకోచం చెంది చక్రం యొక్క లోపలి రిమ్మును గట్టిగా ఒడిసిపట్టుకుంటాయి. ఈవిధంగా హైడ్రాలిక్ బ్రేకులు పనిచేస్తాయి.

ప్రశ్న 5.
ద్రవస్థితిక విరోధభాసం (hydrostatic paradox) అంటే ఏమిటి?
జవాబు:

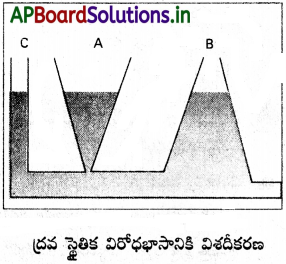
మూడు పాత్రలు A, B, C లు భిన్న ఆకారాలు కలిగి ఉన్నాయి. వాటి అడుగుభాగాన్ని ఒక క్షితిజ సమాంతర గొట్టం సంధానం చేస్తోంది. వాటిని నీటితో నింపినప్పుడు ఆ మూడు పాత్రలలోను నీటిమట్టం వాటిలో నిలిచి ఉన్న నీటి మొత్తాలు భిన్నమైనప్పటికీ, ఒకటిగానే ఉంది. ఇలా ఎందుకు జరుగుతుందంటే, పాత్ర యొక్క ఒక్కొక్క భాగం అడుగులో నీరు కలిగించే పీడనం సమానంగా ఉంటుంది. దీనినే ద్రవస్థైతిక విరోధ భాసం అంటారు.

ప్రశ్న 6.
లోతుతో పీడనం ఎలా మారుతుందో వివరించండి.
జవాబు:
పాత్రలో ప్రవాహి నిశ్చలస్థితిలో ఉందనుకొనుము. పటంలో బిందువు 1, బిందువు 2 కన్నా h ఎత్తులో ఉంది. 1 మరియు 2 బిందువుల వద్ద పీడనాలు P₁ మరియు P₂. ప్రవాహి నిశ్చలంగా ఉంది కాబట్టి, క్షితిజ సమాంతర బలాలు శూన్యం. ఫలిత క్షితిజ లంబ బలాలు, భారానికి సమానం. పైతలం వద్ద పీడనం క్రిందకు పనిచేస్తుంది (P₁A), అడుగున పీడనం (P₂A) పైకి పనిచేస్తుంది.
(P₂ – P₁) A = mg …………… (1)
ప్రవాహి యొక్క ద్రవ్యరాశి (m) = ρv = ρhA
(P₂ – P₁) = ρgh …………. (2)

పీడనాలలో తేడా క్షితిజ లంబ ఎత్తు h పై ఆధారపడుతుంది.

ఇప్పుడు బిందువు 1ని ప్రవాహి (నీరు) ఊర్థ్వతలంపైకి మారిస్తే, అది తెరచి ఉంది కనుక P₁ కి బదులుగా వాతావరణ పీడనం (P_a) ని మరియు P₂ కి బదులుగా P ని మారిస్తే,
సమీకరణం (2) నుండి, P – P_a = ρgh
P = P_a + ρgh

ద్రవం అడుగున పీడనం P, తెరచిన చోట ద్రవం యొక్క వాతావరణ పీడనం కన్నా ρgh పీడనం అధికంగా ఉంటుంది.

ప్రశ్న 7.
టోరిసెల్లి నియమం అంటే ఏమిటి? ఒక ప్రయోగంతో బహిస్రావం (efflux) వడిని ఎలా నిర్ధారిస్తారో వివరించండి.
జవాబు:
టోరిసెల్లి నియమం :
బహిస్రావం (efflux) అనే పదానికి అర్థం ప్రవాహి బయటకు వెళ్ళడం. ఒక తెరచిన తొట్టి (టాంక్) నుంచి ఉండే బహిస్రావ వడి స్వేచ్ఛగా కిందకు పడుతున్నపుడు వర్తించే ఫార్ములాకు సరిసమానమైన రూపాన్ని కలిగి ఉంటుంది. దీనినే టోరిసెల్లి నియమం అంటారు.

ρ సాంద్రత గల ఆదర్శద్రవం టాంక్లో నింపబడినది అనుకొనుము. ఆ టాంక్కు సన్నని రంధ్రం కలదు.

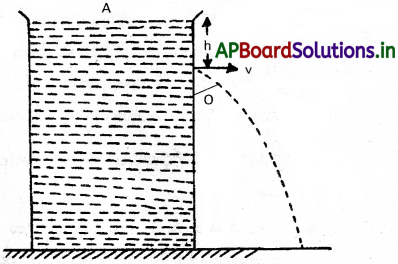
Oబిందువు నుండి ద్రవం యొక్క ఎత్తు h అనుకొనుము.
P = వాతావరణ పీడనం
V = రంధ్రం వద్ద ప్రవాహ వేగం
A మరియు O వద్ద బెర్నూలీ సిద్ధాంతంను అన్వర్తించగా
(P + ρgh + O)_{Aవద్ద} = (P + 0 + \(\frac{1}{2}\)ρν²)_{Oవద్ద}
P + ρgh = P + \(\frac{1}{2}\)ρν² ⇒ ρgh = \(\frac{1}{2}\)ρν²
V = √2gh

ప్రశ్న 8.
వెంటూరి – మీటర్ అంటే ఏమిటి ? దీన్ని ఎలా ఉపయోగిస్తారో వివరించండి.
జవాబు:

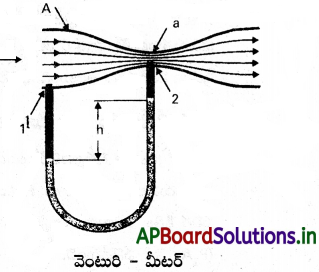
వెంటురి-మీటర్ :
అసంపీడ్య ప్రవాహి యొక్క ప్రవాహ వడిని కొలిచే సాధనమే వెంటురి-మీటర్.

1. ఒక విశాలమైన వ్యాసంతో, మధ్యలో ఒక చిన్న నొక్కును కలిగి ఉన్న ఒక గొట్టాన్ని ఈ వెంటురి- మీటర్ కలిగి ఉంటుంది.
2. U- ఆకారంలో ఉన్న ఒక మానోమీటర్ దీనికి అనుసంధానించి ఉంటుంది. మానోమీటర్ యొక్క ఒక భుజం వెంటురి మీటర్ గొట్టం యొక్క వెడల్పాటి మెడ వైశాల్యం కలిగిన కొనకు, మరోభుజం వెంటురి మీటరు మధ్య భాగంలో ఉన్న నొక్కుకు కలపబడి ఉంటాయి.
3. మానోమీటర్లో p సాంద్రతగల ఒక ద్రవం ఉంటుంది.
4. పీడన వ్యత్యాసం, ఇరుకైన కొనవద్ద కలిపిన U-గొట్టంలోని ప్రవాహి మట్టం మిగతా భుజంలోని ప్రవాహి మట్టం కంటే పెరిగేటట్లు చేస్తుంది.
5. వడపోతచేసే పంపులు, సుగంధ ద్రవ్యాలను వెదజల్లడానికి ఉపయోగించే స్ప్రేయర్లు, ఆటోమొబైల్స్లో ఉండే కార్బ్యురేటర్లు అన్నీ ఈ సూత్రంపైనే ఆధారపడి పనిచేస్తాయి.

ప్రశ్న 9.
రెనాల్డ్స్ సంఖ్య అంటే ఏమిటి? దాని ప్రాముఖ్యత ఏమిటి?
జవాబు:
రెనాల్డ్స్ సంఖ్య :
గొట్టంలో ప్రవహించే ద్రవాల స్వభావాలను తెలిపే సంఖ్యను రెనాల్డ్స్ సంఖ్య అంటారు.
రెనాల్డ్స్ సంఖ్య (R_e) = \(\frac{\rho v \mathrm{~d}}{\eta}\)
ఇక్కడ p అనునది ప్రవాహి సాంద్రత
V అనునది ప్రవాహి వేగం, d అనునది గొట్టం యొక్క వ్యాసం
i) R_e < 1000 అయితే ప్రవాహం ధారా రేఖాప్రవాహం (లేదా) స్తరీయంగా ఉంటుంది.
ii) R_e > 2000 అయితే సంక్షుబ్ధ ప్రవాహం.
iii) 1000 < R_e < 2000 అయితే ప్రవాహం ధారారేఖ, సంక్షుభ్ర దశలమధ్య మారుతూ ఉంటుంది.

రెనాల్డ్స్ సంఖ్య యొక్క భౌతిక ప్రాముఖ్యత :
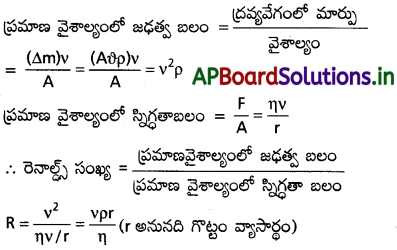
ప్రమాణ వైశాల్యంలో జఢత్వ బలానికి, స్నిగ్ధతా బలానికి గల నిష్పత్తి రెనాల్డ్స్ సంఖ్యను సూచిస్తుంది.

ప్రశ్న 10.
గతిక ఉత్థాపనాన్ని ఉదాహరణలతోసహా వివరించండి.
జవాబు:
గతిక ఉత్థాపన :
వస్తువు ప్రవాహి గుండా ప్రయాణించినప్పుడు, దానిపై పనిచేసే ఊర్థ్వబలాన్ని గతిక ఉత్థాపన అంటారు.

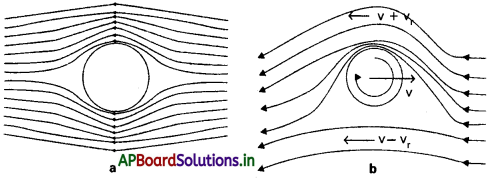
ఉదా :
పటం (a)లో బంతి స్పిన్ రహితంగా ఒక ప్రవాహికి సాపేక్షంగా చలిస్తున్న బంతిపైభాగంలోను, కిందిభాగంలోను ధారారేఖలు సమానంగా విస్తరించి ఉంటాయి. బంతిపై భాగంలోను, కిందిభాగంలోను వేగం ఒకేవిధంగా ఉండి, పీడనాలలో తేడా శూన్యం అవుతుంది. అందువల్ల బంతి మీద ఊర్థ్వంగాకాని, అధోముఖంగా కాని ఏవిధమైన బలం పనిచేయదు.

పటం (b)లో బంతి స్పిన్ గమనంలో ఉన్నప్పుడు ధారారేఖలు బంతి పైభాగంలో అధికంగాను, కిందిభాగంలో తక్కువగాను వ్యాపిస్తాయి. బంతి పైభాగంలో వేగం (v + v) అధికంగాను, కిందిభాగంలో వేగం (v – v.) తక్కువగాను ఉంటుంది. దీనివలన కింద, పైతలాలపై పీడనాలలో తేడా ఏర్పడుతుంది. బంతిపై భాగంలో పీడనం తక్కువగాను, కిందిభాగంలో పీడనం ఎక్కువగాను ఉంటుంది. కాబట్టి బంతిపై నికర ఊర్ధ్వాభిముఖ బలం పనిచేస్తుంది.

ఉదా 2 :
విమానం రెక్కపై కూడా గతిక ఉత్థాపన పనిచేస్తుంది.

ప్రశ్న 11.
తలతన్యత, తలశక్తులను వివరించండి. [Mar. ’13]
జవాబు:
తలతన్యత(S) :
ద్రవతలంపై ఒక సరళరేఖను ఊహించినపుడు, ద్రవతలంపై ఏకాంక పొడవుపై, ఆ పొడవుకు లంబంగా పనిచేసే బలాన్ని తలతన్యత అంటారు.
T = \(\frac{F}{l}\)
S.I ప్రమాణం → N/m
మితిసూత్రం → [MT^-2]

ఉపరితలశక్తి (E) :
అణుబలాలవల్ల ప్రమాణవైశాల్యంలో గల అధిక స్థితిజ శక్తిని ఉపరితలశక్తి అంటారు.

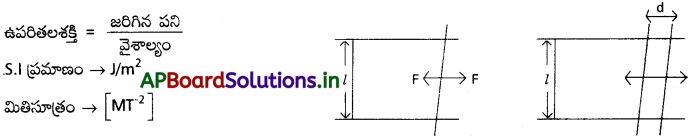
ఒక క్షితిజ సమాంతర ద్రవపు పొరను పరిగణించండి. ఈ పొర సమాంతర సూచికల మీదుగా జారగలిగే స్వేచ్ఛ ఉన్న దండం వద్ద అంతమవుతుంది. ఒకవేళ మనం దండాన్ని d అనే స్వల్పదూరం జరిపామనుకొందాం. అప్పుడు పొర తల వైశాల్యం పెరుగుతుంది. కాబట్టి, ఈ వ్యవస్థ ఇంతకు ముందు కంటే ఎక్కువ శక్తిని కలిగి ఉంటుంది. అంటే ఒక అంతర్గత బలానికి వ్యతిరేకంగా కొంతపని జరిగిందని అర్థం. ఈ అంతర్గతబలం F అనుకొందాం.
జరిగిన పని (W) = F.d

ఆ పొర యొక్క ఏకాంక వైశాల్యానికి తలశక్తి S అయితే అదనంగా కలిగిన వైశాల్యం 2dl. ద్రవానికి రెండు తలాలు ఉంటాయి.

అదనపు శక్తి S (2dl) = Fd
S = \(\frac{F}{2l}\)

ద్రవ ఉమ్మడి తలం యొక్క ఏకాంక వైశాల్యానికి గల తలశక్తి ఈ తలతన్యతకు సమానం. అంతేగాక, కదలడానికి వీలున్న దండం ఏకాంక పొడవుపై ప్రవాహి ప్రయోగించే బలానికి కూడా తలతన్యత సమానమవుతుంది.

ప్రశ్న 12.
ప్రయోగాత్మకంగా తలతన్యతను కనుక్కొనే విధానాన్ని వివరించండి.
జవాబు:

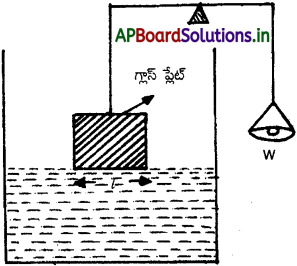
ఒక చదునైన నిట్టనిలువు గాజుపలక, దానికింద ఏదో ఒక ద్రవమున్న పాత్ర ఉన్నప్పుడు, అది త్రాసుయొక్క ఒక భుజంగా రూపొందుతుంది. ఈ గాజుపలక క్షితిజ సమాంతర అంచుపాత్రలోని నీటికి కొద్దిగా పైన ఉన్నప్పుడు, దాన్ని త్రాసు మరో చివరన ఉంచిన బరువులు సంతులనం చేస్తాయి. ఇప్పుడు గాజుపలక అంచుకు కొద్దిగా మాత్రమే ద్రవం తగిలేవరకు పాత్రను కొంచెం పైకి ఎత్తుతారు. అప్పుడు ఆ ద్రవం, దాని తలతన్యతమూలంగా గాజుపలకను కొంచెం కిందకు లాగుతుంది. గాజుపలక, నీటిని తప్పించుకొని కొంచెం పైకి వచ్చేవరకు రెండో చివర బరువులను వేస్తూపోతారు. అదనంగా వేసిన బరువును W అనుకొందాం. ద్రవం – గాలి ఉమ్మడితలం యొక్క ‘తలతన్యత
S_la = \(\frac{w}{2l}\frac{mg}{2l}\)

ఇక్కడ m అదనపు ద్రవ్యరాశి, l గాజుపలక అంచుపొడవు.

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 1.
బెర్నౌలీ సూత్రాన్ని తెలపండి. ఒక గొట్టంలో ప్రవహిస్తున్న శక్తి నిత్యత్వ నియమాన్ని అనువర్తించి బెర్నౌలీ సమీకరణాన్ని రాబట్టండి. బెర్నౌలీ సిద్ధాంతానికి ఒక అనువర్తనాన్ని ఇవ్వండి.
జవాబు:
బెర్నౌలీ సూత్రం :
గొట్టంలో స్థిరవేగంతో ప్రవహిస్తున్న స్నిగ్ధత లేని అసంపీడ్య ప్రవాహంలో ఏకాంక ఘనపరిమాణం గల ప్రవాహి పీడనశక్తి, గతిజశక్తి, స్థితిజశక్తి ఏ బిందువు వద్దనైనా స్థిరం. దీనినే బెర్నౌలీ సూత్రం అంటారు.

P + \(\frac{1}{2}\) ρv² + ρgh స్థిరం

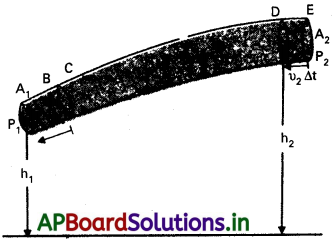
i) ఒక గొట్టం గుండా స్నిగ్ధతారహితం, అసంపీడ్య ప్రవాహి ధారారేఖా ప్రవాహంలో ఉంది అనుకొనుము.

ii) BC మరియు DE అను రెండు ప్రాంతాలలో ప్రవాహాన్ని తీసుకుందాం. తొలిగా ప్రవాహి B మరియు D బిందువుల వద్ద ఉందనుకొనుము.

iii) ∆t కాలంలో, B బిందువు వద్ద ప్రవాహి వేగం V₁ మరియు D బిందువు వద్ద వేగం V₂ అనుకొనుము.

iv) ∆t కాలంలో B నుండి C కి ప్రవాహి ప్రయాణించిన దూరం V₁ ∆t. అదేకాలంలో D నుండి Eకి ప్రవాహి ప్రయాణించిన దూరం V₂∆t.

v) A₁ మరియు A₂ అడ్డుకోత వైశాల్యాల వద్ద పీడనాలు P₁ మరియు P₂ అనుకొనుము.

vi) ఎడమ చివర BC వద్ద ప్రవాహి మీద జరిగిన పని = బలం × స్థానభ్రంశం
= పీడనం × వైశాల్యం × స్థానభ్రంశం
= P₁ A₁ × V₁ ∆t (∵ ∆V = A₁V₁∆t)
= P₁ ∆V ………….. (1)

vii) కుడివైపు చివర DE వద్ద ప్రవాహి చేసిన పని
= P₂ A₂ × V₂dt = P₂ ∆V ………….. (2)

viii) ప్రవాహి పై జరిగిన పని ధనాత్మకం మరియు ప్రవాహి చేసిన పని ఋణాత్మకంగా తీసుకుంటే
మొత్తం పని (W) = (P₁ – P₂) ∆V ……………. (3)
ఈ పనిలో కొంత భాగం ప్రవాహి గతిజశక్తిలో మార్పుకు మిగిలిన భాగం స్థితిజశక్తిలో మార్పుకు ఉపయోగపడుతుంది.

ix) at కాలంలో గొట్టంలో ప్రవహించిన ప్రవాహి ద్రవ్యరాశి (Am)
= ρA₁V₁∆t
ఇక్కడ p అనునది ప్రవాహి యొక్క సాంద్రత
∆m = ρ∆V …………… (4)

x) గురుత్వ స్థితిజశక్తి ρg∆V (h₂ – h₁) …………… (5)
గతిజశక్తిలో మార్పు (∆K) = \(\frac{1}{2}\)ρ∆V (V²₂ – V²₁) …………..(6)

xi) శక్తి నిత్యత్వనియమం ప్రకారం

∴ ప్రమాణ ఘనపరిమాణంలో పీడనశక్తి, గతిజశక్తి మరియు స్థితిజశక్తుల మొత్తం స్థిరం.

బెర్నౌలీ సిద్ధాంతం అనువర్తనాలు:

1. ఈ సిద్ధాంతం విమానం రెక్కపై గతిక ఉత్థాపనను వివరిస్తుంది.
2. ఇది స్పిన్ గమనంలో ఉన్న క్రికెట్ బంతిపై గతిక ఉత్థాపనను వివరిస్తుంది.

ప్రశ్న 2.
స్నిగ్ధతా గుణకాన్ని నిర్వచించండి. స్టోక్స్ నియమాన్ని వివరించి, ఏ పరిస్థితులలో ఒక వర్షపు బిందువు చరమవేగం υ_tని పొందుతుందో వివరించండి. υ_tకి సమీకరణాన్ని ఇవ్వండి.
జవాబు:
స్నిగ్ధతా గుణకం (n) :
ప్రవాహి దిశకు లంబంగా ఉన్న పొరల మధ్య ఏకాంక వేగ ప్రవణత ఉన్నపుడు, ఏకాంక వైశాల్యంగల పొరల మీద పనిచేసే స్నిగ్ధతా బలాన్ని స్నిగ్ధతా గుణకం అంటారు.

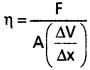
S.I. ప్రమాణాలు → Nm^-2 s (లేదా) P_aS
C.G.S ప్రమాణాలు → పాయిజ్ (Poise)
మితిసూత్రం = [ML^-1T^-1]

స్టోక్స్ నియమం :
ఈ నియమం ప్రకారం గోళాకార వస్తువుపై పనిచేయు స్నిగ్ధతా బలం
i) ప్రవాహి స్నిగ్ధతా గుణకానికి (η)
ii) గోళాకార వస్తువు వ్యాసార్థం (r) కు
iii) వస్తువు యొక్క వేగం (v) కి అనులోమానుపాతంలో ఉంటుంది.
∴ F a ηrv
F = k ηrv

ఇక్కడ K అనునది అనుపాత స్థిరాంకం. ప్రయోగపూర్వకంగా దీని విలువను 67 గా కనుగొన్నారు.
∴ F = 6πηrv

మేఘాల నుండి గురుత్వాకర్షణ బలాల వల్ల క్రిందకు పడే వర్షపు చినుకులు దాదాపు స్థిరవేగంతో భూమిని చేరతాయి. ఈ వేగాన్ని అంత్యవేగం అంటారు. అంత్య వేగాన్ని పొందిన తర్వాత, వర్షపు బిందువుపై ఫలితబలం శూన్యం. స్టోక్స్ నియమం ప్రకారం, F α ηrv
F = 6πηv (∵ K = 6π = అనుపాత స్థిరాంకం)
ρ మరియు r లు గోళాకార బిందువు సాంద్రత మరియు వ్యాసార్థాలు.
ప్రవాహి సాంద్రత σ అనుకొనుము.
గోళాకార బిందువు పై బలాలు
i) బిందువు భారం W = mg
W = Vρg = \(\frac{4}{3}\)πr³ρg ……………. (1)

ii) ఉత్తవన బలం (B) = V a g = \(\frac{4}{3}\)πr³ σg …………. (2)

iii) స్నిగ్ధతాబలం (f) = 6ηrν ………… (3)
గోళాకార ద్రవబిందువు అంత్యవేగాన్ని (vi) పొందితే, దానిపై ఫలితబలం శూన్యం.
∴ అంత్యవేగం వద్ద ఫలిత అధోబలం = ఫలిత ఊర్థ్వబలం
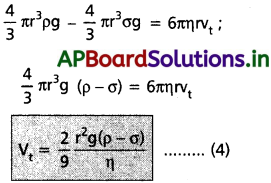
W = B + f, W – B = f

లెక్కలు (Problems)

ప్రశ్న 1.
0.6 cm వ్యాసంగల ఒక సబ్బు బుడగను ఊదేందుకు తలతన్యతా బలానికి వ్యతిరేకంగా చేయాల్సిన పనిని లెక్కించండి. (సబ్బు ద్రావణం తలతన్యత = 2.5 x 102 Nm−1).
సాధన:
D = 0.6 cm = 0.6 × 10^-2
r = \(\frac{D}{2}=\frac{0.6 \times 10^{-2}}{2}\) = 0.3 × 10^-2 m
S = 2.5 × 10^-2 N/m
W = 8πr²s
= 8 × 3.14 × (0.3 × 10^-2)² × 2.5 × 10^–
W = 5.652 × 10^-6J

ప్రశ్న 2.
0.06 cm వ్యాసం గల గాజుగొట్టంలో మిథైల్ ఆల్కహాల్ ఎంత ఎత్తుకు ఎగబాకుతుంది? (మిథైల్ ఆల్కహాల్ తలతన్యత = 0.023 Nm^-1, సాంద్రత gmcm^-3. స్పర్శకోణాన్ని శూన్యంగా పరిగణించండి)
సాధన:

ప్రశ్న 3.
నీటిలో ముంచిన కేశనాళం వ్యాసార్ధం ఎంత ఉండే దానిలో నీరు 6 cm ఎత్తుకు ఎగబాకుతుంది? (నీటి తలతన్యత = 7.2 × 10^-2 Nm^-1)
సాధన:
h = 6 × 10^-2 m, S = 7.2 × 10^-2 N/m
నీటి యొక్క సాంద్రత (ρ) = 10³ kg/m³

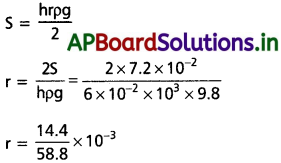
r = 0.24 × 10^-3
r = 0.24 m.m

ప్రశ్న 4.
0.4 mm వ్యాసంగల ఒక కేశనాళికను బీకరులో ఉన్న పాదరసంలో ముంచినప్పుడు, నాళంలోని ద్రవచంద్ర రేఖాకృతి (meniscus) లో కలిగే నిమ్నతను లెక్కించండి. (పాదరసం సాంద్రత 13.6 × 10³Kg m^-3, పాదరసం తలతన్యత = 0.49 Nm ^-1, స్పర్శకోణం = 135°)
సాధన:

ఇక్కడ ఋణగుర్తు పాదరస మట్టం క్రిందకు పడిపోవుటను సూచిస్తుంది.

ప్రశ్న 5.
ఒక సబ్బు బుడగ వ్యాసం 10mm. దాని తలతన్యత 0.04 Nm^-1. ఆ బుడగలోని అదనపు పీడనాన్ని కనుక్కోండి. [Mar. ’14]
సాధన:
D = 10 m.m

ప్రశ్న 6.
R వ్యాసార్ధం గల బుడగను రూపొందించేందుకు చేసిన పని W అయితే బుడగ వ్యాసార్ధం రెట్టింపు అయ్యేందుకు (2R అయ్యేందుకు) ఎంత శక్తి అవసరం?
సాధన:
R₁ = R, R² = 2R
తొలి పని (W) = 8πR²s
తుది పని (W) = 8π[4R₂² – R₁² ]S
= 8π [4R² – R²]S
= 3 × 8π R²S
W’ = 3W

ప్రశ్న 7.
R₁, R₂ వ్యాసార్థాలు గల రెండు సబ్బు బుడగలు శూన్యంలో సమోష్ణోగ్రతా ప్రక్రియ పరిస్థితులో కలిసిపోయి ఒక బుడగను ఏర్పరచాయి. ఆ కొత్త బుడగ వ్యాసార్ధం ఎంత? సబ్బు ద్రావణం తలతన్యతను T గా తీసుకోండి.
సాధన:
R₁, R₂ మరియు R అనునవి మొదటి, రెండవ మరియు ఫలిత బుడగల వ్యాసార్థాలు అనుకొనుము. సబ్బు బుడగలు శూన్యంలో కలిస్తే, ఉపరితల శక్తి మారదు.

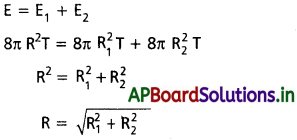
అదనపు లెక్కలు (Additional Problems)

ప్రశ్న 1.
ఎందుకో వివరించండి
a) మనిషి శరీరంలో పాదాల వద్ద రక్తపీడనం మెదడు వద్ద కంటే ఎక్కువ.
b) భూమి నుంచి 100km కంటే ఎక్కువగా వాతా వరణం ఉన్నప్పటికీ 6 km ఎత్తువద్ద వాతావరణ పీడనం, సముద్రమట్టం వద్ద ఉండే వాతావరణ పీడనంలో సగం ఉంటుంది.
c) బలాన్ని, వైశాల్యంతో భాగిస్తే వచ్చేదే పీడనం అయినప్పటికీ ఈ ద్రవస్థితిక పీడనం ఒక అదిశరాశి.
సాధన:
a) మానవ శరీరంలో రక్తం స్తంభం ఎత్తు, మెదడు కన్నా అడుగు ఎత్తులో ఎక్కువగా ఉండాలి. అందుకు కారణం, అడుగు ఎత్తులో ఉండుటవల్ల రక్తం అధిక పీడనాన్ని కలిగిస్తుంది.

b) భూమి ఉపరితలం వద్ద గాలి సాంద్రత అధికంగా ఉంటుంది. ఎత్తుకు పోయేసరికి అది తగ్గుతుంది. సముద్ర మట్టానికి 6 km ఎత్తుకు పోయేసరికి అది దాదాపు సగానికి తగ్గుతుంది. 6 km ఎత్తు దాటిన తర్వాత, గాలి సాంద్రత ఎత్తుతో పాటు నెమ్మదిగా తగ్గుతుంది. ఈ కారణం చేత సముద్రమట్టం నుండి 6 km ఎత్తుకు పోయేసరికి, వాతావరణ పీడనం దాదాపు సగానికి తగ్గుతుంది.

c) ద్రవంపై బలాన్ని కలిగిస్తే, ఆ పీడనం అన్ని దిశలలో సమానంగా ప్రసరిస్తుంది. అందుకని ద్రవం వల్ల కలిగే పీడనానికి దిశ ఉండదు. కాబట్టి ద్రవపీడనం అదిశరాశి.

ప్రశ్న 2.
ఎందుకో వివరించండి.
a) గాజుతోపాదరసం స్పర్శకోణం గురుకోణం కాని నీటితో లఘుకోణం.
b) శుభ్రమైన గాజుపలక తలంపై వేసిన నీరు దానిపై వ్యాపించడానికి ప్రయత్నిస్తుంది. కాని పాదరసం అయితే బిందువులుగా ఏర్పడటానికి ప్రయత్నిస్తుంది. (దీన్నే ఇంకోరకంగా చెప్పాలంటే, నీరు గాజును తడుపుతుంది. కాని పాదరసం గాజును తడపలేదు.)
c) ఒక ద్రవం తలతన్యత ఆ తలవైశాల్యంపై ఆధారపడి ఉండదు.
d) డిటర్జంట్ కలిపిన నీరు తక్కువ స్పర్శకోణాలను కలిగి ఉంటుంది.
e) బాహ్య బలాలకు లోనుకానటువంటి ద్రవబిందువు ఎప్పుడూ గోళాకారాన్నే కలిగి ఉంటుంది.
సాధన:
a) ఒక ఘనపదార్థంపై కొద్దిగా ద్రవాన్ని పోస్తే, ద్రవం -గాలి, ఘనపదార్థం-గాలి మరియు ఘనపదార్థం- ద్రవం అనే మూడు అంతఃతలాలు ఏర్పడతాయి. ఈ మూడు తలాల తలతన్యతలు S_LA, S_SA మరియు S_SL. θ అనునది ద్రవం మరియు ఘనపదార్థం మధ్య స్పర్శ కోణం. ఈ మూడు తలాలు కలిసేచోట అణువులు సమతాస్థితిలో ఉంటాయి. దాని అర్థం ఫలిత బలం శూన్యం. 0 వద్ద సమతాస్థితిలో ఉన్న అణువుకు

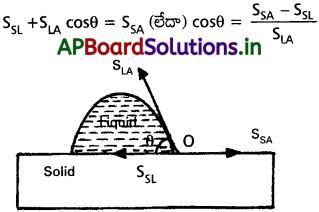
పాదరసం-గాజులో, S_SA < S_SL, ఇక్కడ cos θ ఋణాత్మకం. (లేదా) θ > 90° అనగా గురుకోణం. నీరు-గాజు తలానికి S_SA > S_SL ఇక్కడ cos θ ధనాత్మకం (లేదా) θ < 90° అనగా లఘుకోణం.

b) పాదరసం-గాజులో స్పర్శకోణం గురుకోణం. ఈ గురుకోణాన్ని పొందడానికి పాదరసం బిందువుగా ఏర్పడుతుంది. నీరు-గాజుకు స్పర్శకోణం లఘు కోణం. ఈ లఘుకోణాన్ని పొందడానికి నీరు విస్తరిస్తుంది.

c) ద్రవతలానికి గీసిన స్పర్శరేఖపై లంబంగా ప్రమాణ పొడవుపై పనిచేసే బలాన్ని ద్రవం యొక్క తలతన్యత అంటారు. బలం ద్రవతలం యొక్క వైశాల్యంపై ఆధారపడదు. కాబట్టి తలతన్యత కూడా ద్రవతల వైశాల్యంపై ఆధారపడదు.

d) వస్త్రాలలో సన్నని రంధ్రాలు కేశనాళికలవలే ఏర్పడతాయి. కేశనాళికలో ఎగబ్రాకే ద్రవం cos eకు అనులోమాను పాతంలో ఉంటుంది. 8 స్వల్పం అయితే cos 8 అధికం. కాబట్టి కేశనాళికీయత పెరిగి వస్త్రం లోకి సబ్బు త్వరగా చొచ్చుకుపోతుంది.

e) బాహ్యబలాలు పని చేయనప్పుడు, తలతన్యత వల్ల ద్రవతలాలు కనిష్ట వైశాల్యాన్ని పొందుటకు ప్రయత్నిస్తాయి. గోళం యొక్క వైశాల్యం కనిష్టం కాబట్టి ద్రవబిందువులు గోళాకారంగా ఉంటాయి.

ప్రశ్న 3.
ప్రతి వాక్యానికి అనుబంధంగా ఇచ్చిన పదాలతో ఖాళీలను పూరించండి.
a) ద్రవాల తలతన్యత ఉష్ణోగ్రతతోపాటు సాధారణంగా.. (పెరుగుతుంది/తగ్గుతుంది)
b) వాయువులు స్నిగ్ధత ఉష్ణోగ్రతతోపాటు …. అదే ద్రవాల స్నిగ్ధత ఉష్ణోగ్రతతోపాటు….. (పెరుగుతుంది/ తగ్గుతుంది)
c) స్థితిస్థాపక ద్రుఢతా గుణకమున్న ఘనపదార్థాల విషయంలో విరూపణ బలం…., కు అనులోమాను పాతంలో ఉంటే ప్రవాహులకు …కు అనులోమాను పాతంలో ఉంటుంది (విరూపణ వికృతి/ విరూపణ వికృతిరేటు)
d) నిలకడ ప్రవాహి ప్రవాహంలో నొక్కు (ఇరుకైన) ప్రాంతంలో ప్రవాహి వడి పెరుగుతుందనేది… అనుసరించి (ద్రవ్యరాశి నిత్యత్వం / బెర్నౌలీ సూత్రం)
e) వాయుసొరంగం (wind tunnel) లో దూసుకు పోతున్న నమూనా విమానానికి సంక్షోభం ఉత్పన్నమయ్యే వేగం, వాస్తవ పరిస్థితులలో ఎగిరే నిజమైన విమానానికి సంక్షోభం ఉత్పన్నమయ్యే వేగం కంటే… (ఎక్కువ/తక్కువ).
సాధన:
a) తగ్గుతుంది

b) పెరుగుతుంది; తగ్గుతుంది.

c) విరూపణ వికృతి; విరూపణ వికృతిలో మార్పురేటు

d) ద్రవ్యరాశి నిత్యత్వం; బెర్నూలీ సిద్ధాంతం

e) అధికం

ప్రశ్న 4.
ఎందుకో వివరించండి
a) ఒక కాగితాన్ని క్షితిజ సమాంతరంగా ఉంచేందుకు నీవు గాలిని దాని కింద నుంచి కాక దానిపైన ఊదాలి.
b) ఒక కుళాయిని కట్టివేసేందుకు దాని మూతిని వేళ్లతో మూయడానికి ప్రయత్నిస్తే మన వేళ్ల మధ్య ఉన్న ఖాళీల నుంచి నీరు వేగంగా బయటకు చిమ్ముకొస్తుంది.
c) ఒక డాక్టరు ఇంజక్షన్ ఇస్తున్నప్పుడు అతడు తన బొటనవేలితో సిరంజిపై ప్రయోగించిన పీడనం కంటే ఆ సిరంజి సూది పరిమాణమే (size) మందు ప్రవాహరేటును అధికంగా ప్రభావితం చేస్తుంది.
d) పాత్రకు ముందువైపున్న ఒక చిన్న రంధ్రం ద్వారా ప్రవాహి వెలుపలికి ప్రవహించేటప్పుడు పాత్రపై ఒక అభిబలం వెనకకు పనిచేస్తుంది. e) ఆత్మభ్రమణం చెందే క్రికెట్ బంతి గాలిలో
పరావలయ పథాన్ని అనుసరించదు.
సాధన:
a) కాగితం మీద గాలిని ఊదితే, గాలివేగం పెరుగుతుంది మరియు దానిపై పీడనం తగ్గుతుంది. (బెర్నూలీ సిద్ధాంతం ప్రకారం), కాగితం అడుగున వాతావరణ పీడనం పని చేసి కాగితం క్షితిజ సమాంతరంగా నిలిచి ఉంటుంది.

b) నీటి జెట్ వైశాల్యం తగ్గితే, సాంతత్య సమీకరణం av = స్థిరం ప్రకారం నీటివేగం పెరుగుతుంది.

c) పాత్రలో చిన్న రంధ్రం గుండా ప్రవాహి బయటకు పోతే, అది ఎక్కువ వేగాన్ని పొందుతుంది మరియు ఎక్కువ ద్రవ్యవేగం ఉంటుంది. వ్యవస్థపై బాహ్యబలం పనిచేయకపోతే, ద్రవ్యవేగ నిత్యత్వ నియమం ప్రకారం పాత్ర తిరోవేగంను పొందుతుంది. దీని ఫలితంగా పాత్ర వలన ప్రచోదనం కలుగును.

d) ఇక్కడ సూది పరిమాణం, ప్రవాహ వేగాన్ని నియంత్రిస్తుంది. మరియు పీడనాన్ని బొటనవేలు పీడనం నియంత్రిస్తుంది. బెర్నూలీ సిద్ధాంతం ప్రకారం P + ρgh + \(\frac{1}{2}\)ρV² = స్థిరం. ఇక్కడ P కి ఘాతం ఒకటి మరియు Vకి ఘాతం రెండు. కాబట్టి వేగం ఎక్కువగా ప్రభావితం అవుతుంది. కాబట్టి అధిక ప్రవాహాన్ని నియంత్రించడానికి సూది ఉత్తమం. e) స్పిన్ గమనంలో ఉన్న బంతి వక్రమార్గంలో ఉంటుంది.

ప్రశ్న 5.
ఎత్తైన మడిమలుండే (heels) చెప్పులను ధరించిన 50 kg ల ద్రవ్యరాశి గల ఒక అమ్మాయి ఒంటి కాలిపై తనను తాను నిలబెట్టుకుంది. చెప్పు మడిమ 1.0cm. వ్యాసంతో వృత్తాకారంగా ఉంది. క్షితిజ సమాంతర నేలపై చెప్పు కలగచేసే పీడనం ఎంత?
సాధన:

ప్రశ్న 6.
టోరిచెల్లీ బారోమీటర్లో పాదరసాన్ని ఉపయోగించాడు. పాస్కల్ 984 kg m^-3 సాంద్రత గల ఫ్రెంచి సారాయి (wine) తో టోరిచెల్లీ బారోమీటర్ను పోలి ఉండేటట్లు మరొక బారోమీటర్ను తయారుచేశాడు. సాధారణ వాతావరణ పీడనాన్ని సూచించే ద్రాక్ష సారాయి స్తంభం ఎత్తు ఎంత?
సాధన:

ప్రశ్న 7.
సముద్రతీర ప్రాంతంలో 10⁹ Pa పీడనాన్ని తట్టుకోగల ఒక నిలువైన నిర్మాణాన్ని రూపొందించారు. సముద్రంలోని ఒక చమురు బావి శిఖర భాగంలో ఉంచడానికి ఈ నిర్మాణం అనువైనదేనా? సముద్రం లోతు దాదాపు 3 km అనుకోండి. సముద్ర ప్రవాహాలను ఉపేక్షించండి.
సాధన:
ఇక్కడ గరిష్ట ప్రతిబలం = 10⁹Pa,
h = 3km = 3 × 10³ m;
p(నీటికి) = 10³kg/m³ మరియు g = 9.8 m/s²

చముర్తు బావిపైన ఉంచేందుకు ఇది తగిన నిర్మాణం, సముద్రపు నీరు కలిగించే పీడనం, గరిష్ట ప్రతిబలం కన్నా తక్కువ.

సముద్రపు నీరు వలన పీడనం P = hρg
3 x 10³ × 10³ x 9.8
= 2.94 × 10⁷ Pa
గరిష్ట ప్రతిబలం 10⁷ Pa కన్నా సముద్రపు నీరు పీడనం 2.94 × 10⁷ Pa తక్కువ. కాబట్టి ఈ నిర్మాణమును చమురు బావి పైభాగంలో ఉంచవచ్చు.

ప్రశ్న 8.
గరిష్ఠంగా 3000 kg ద్రవ్యరాశి గల కార్లను ఎత్తగల హైడ్రాలిక్ లిఫ్ట్ను తయారుచేశారు. బరువులను ఎత్తే ముషలకం మధ్యచ్ఛేద వైశాల్యం 425 cm’ అయితే చిన్న ముషలకం భరించగల గరిష్ఠ పీడనం ఎంత?
సాధన:
పెద్ద ముషలకంపై పనిచేసే గరిష్ట బలం
F = 3000 kgf = 3000 × 9.8 N
∴ ముషలకం వైశాల్యం A = 425 cm²
= 425 × 10^-4 m²
∴ పెద్దముషలకంపై గరిష్ట పీడనం,
P = \(\frac{F}{A}=\frac{3000 \times 9.8}{425 \times 10^{-4}}\) = 6.92 × 10⁵ Pa
ద్రవం, పీడనాన్ని సమానంగా ప్రసారం చేస్తుంది. కాబట్టి చిన్నముషలకం భరించే గరిష్ట పీడనం 6.92 × 10⁵ Pa.

ప్రశ్న 9.
U- ఆకార గొట్టంలో పాదరసంతో వేరుచేసిన నీరు, మిథిలేటెడ్ స్పిరిట్ ద్రవస్తంభాలు ఇరువైపులా ఉన్నాయి. నీటిమట్టం 10.0 cm స్పిరిట్ మట్టం ఎత్తు 12.5cm ఉండే విధంగా రెండు భుజాల్లో పాదరస మట్టం ఉంది. స్పిరిట్ విశిష్ట గురుత్వం ఎంత?
సాధన:
U–గొట్టంలో ఒక భుజంలో నీటిస్తంభం ఎత్తు,
h₁ 10.0 cm; ρ₁(సాంద్రత) = 1g cm^-3
U-గొట్టంలో మరొకభుజంలో సారా స్తంభం ఎత్తు,
h₂ = 12.5 cm; ρ₁ = ?

U-గొట్టంలో పాదరస మట్టం రెండు భుజాలలో సమానంగా ఉంటుంది. కాబట్టి ప్రతిదానిపై కలిగే పీడనం సమానం.

ప్రశ్న 10.
ఇంతకు ముందు లెక్కలోని గొట్టంలోని సంబంధిత భుజాల్లో 15.0 cm మట్టం పెరిగే విధంగా నీరు, స్పిరిట్లను అదనంగా కలిపితే, రెండు భుజాల్లోని పాదరస మట్టాలలోని వ్యత్యాసం ఎంత? (పాదరసం విశిష్ఠ గురుత్వం = 13.6)
సాధన:
U- గొట్టంలో ప్రతి భుజంలో సారాను కలిగి ఉన్నప్పుడు, 15.0 cm ఎత్తున నీటిని పోస్తే, సారా కలిగిన భుజం వైపు పాదరస మట్టం పెరుగుతుంది. U-గొట్టం రెండు భుజాలలో పాదరస మట్టాలలో తేడా, ρ అనునది పాదరస సాంద్రత h cm పాదరస స్తంభం కలిగించే పీడనం నీరు మరియు సారా కలిగించే పీడనాలలో తేడా.
∴ hρg = h₁ρ₁g – h₂ρ₂g ………… (i)
ఇక్కడ h = ?; ρ =13.6 g cm^-3
ρ₁ = 1 g cm^-3
ρ₂ = 0.8 g cm^-3
h₁ = 15 + 10 = 25 cm
h₂ = 15 + 12.5 = 27.5 cm

ఈ విలువలను (i)లో ప్రతిక్షేపించగా
h × 13.6 × g
= 25 × 1 × g – 27.5 × 0.8 x g = 3g
(లేదా) h 3/13.6 0.22cm

ప్రశ్న 11.
నదిలో నీటి ప్రవాహం ఉధృతంగా ఉన్న ప్రాంతంలో (rapid) ఆ నీటి ప్రవాహాన్ని వర్ణించేందుకు బెర్నౌలీ సమీకరణాన్ని ఉపయోగించవచ్చా? వివరించండి.
సాధన:
లేదు. బెర్నూలీ సిద్దాంతం కేవలం ధారారేఖా ప్రవాహంలో మాత్రమే ఉపయోగిస్తారు.

ప్రశ్న 12.
బెర్నౌలీ సమీకరణాన్ని అనువర్తించేటప్పుడు పరమ పీడనానికి బదులు గేజ్ పీడనాన్ని ఉపయోగిస్తే ఏదైనా ప్రభావం ఉంటుందా? వివరించండి.
సాధన:
లేదు. బెర్నూలీ సమీకరణంకు అన్వర్తించుటకు పరమ పీడనానికి బదులు పరిమాణం చూచు పరికరాన్ని రెండు బిందువుల మధ్య వాతావరణ పీడనాన్ని కొలుచుటకు ఉపయోగిస్తారు. బెర్నూలీ సమీకరణంను అన్వర్తించడాన్ని సాధన. విమానం రెక్క పైభాగం మరియు క్రింది భాగాలలో ప్రత్యేకంగా గుర్తుంచుకోవాలి.

ప్రశ్న 13.
1.5 m పొడవు, 1.0 cm. వ్యాసార్థంగల ఒక క్షితిజ సమాంతర గొట్టం ద్వారా గ్లిజరిన్ నిలకడగా ప్రవహిస్తున్నది. గొట్టం ఒక చివర ఒక సెకన్ కాలంలో సేకరించిన గ్లిజరిన్ పరిమాణం 4.0 × 10^-3 kg s^-1 అయితే గొట్టం రెండు చివరల మధ్య ఉండే పీడన వ్యత్యాసం ఎంత ? (గ్లిజరిన్ సాంద్రత = 1.3 × 10³kg m^-3, గ్లిజరిన్ స్నిగ్ధత : 0.83 Pa s). (గొట్టంలోని ప్రవాహం స్తరీయం అనే మీ ఊహ సరైందా ? లేదా ? అని పరీక్షించడంలో మీరు ఆసక్తికనబరచవచ్చు).
సాధన:
ఇక్కడ, l = 1.5 m, r = 1.0 cm = 10^-2 m,
ρ = 1.3 × 10³ kg/m³; η = 0.83 Nsm^-2.

సెకనుకు ప్రవహించే గ్లిజరిన్ ద్రవ్యరాశి,
M = 4 × 10^-3 kg/s

గొట్టం రెండు చివరలలో పీడనాలలో తేడా P అయితే, పాయిజీ సూత్రం ప్రకారం

ప్రశ్న 14.
ఒక వాయు సొరంగంలో నమూనా విమానాన్ని పరీక్షించే ప్రయోగంలో విమాన రెక్కల పైతలం, కింది తలంపై ప్రవాహ వడులు వరుసగా 70 m s^-1, 63 m s^-1. విమానరెక్క వైశాల్యం 2.5 m² అయితే దానిపై పనిచేసే ఉత్థాపక బలాన్ని లెక్కగట్టండి. గాలి సాంద్రతను 1.3 kg m^-3 గా తీసుకోండి.
సాధన:
విమాన రెక్క పైభాగంలో మరియు క్రింది భాగలలో వేగాలు V₁, V₂ అనుకొనుము.

P₁ మరియు P₂లు రెక్క పైభాగంలో మరియు క్రింది భాగంలో పీడనాలు.
V₁ = 70ms^-1; V₂ = 63ms^-1,
ρ = 1.3kg m^-3.
బెర్నూలీ సిద్ధాంతం నుండి,

ఈ పీడనాలలో తేడా, విమానంను పైకి లేపుతుంది.
కాబట్టి విమానంపై ఊర్థ్వ బలం = పీడనంలో తేడా × విమానం రెక్క వైశాల్యం
= 605.15 × 2.5
= 1512.875 N
= 1.51 × 10³N.

ప్రశ్న 15.
పటాలు 11.23 (a), (b) లు స్నిగ్ధతారహిత ద్రవం నిలకడ ప్రవాహాన్ని సూచిస్తున్నాయి. అప్పుడు ఈ రెండు పటాల్లో ఏది సరైంది కాదు? ఎందువల్ల?

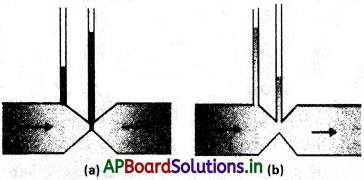
సాధన:
పటం (a) సరియైనదికాదు. సాంతత్య సమీకరణం ప్రకారం av = స్థిరం. ఇక్కడ అడ్డుకోత వైశాల్యం ‘a’ తగ్గితే, ప్రవహించే ద్రవవేగం పెరుగుతుంది. కాబట్టి గొట్టంలో నొక్కబడిన భాగం వద్ద ద్రవవేగం గొట్టం మిగిలిన భాగం కన్నా ఎక్కువ. బెర్నూలీ సిద్ధాంతం ప్రకారం P + \(\frac{1}{2}\)ρv² = స్థిరం.
ఇక్కడ V ఎక్కువైతే, P తగ్గును (లేదా) P పెరిగితే V తగ్గుతుంది.

ప్రశ్న 16.
ఒక స్ప్రే పంప్ స్తూపాకార గొట్టం మధ్యచ్ఛేద వైశాల్యం 8.0 cm² దాని ఒక చివర 1.0 mm వ్యాసంగల సూక్ష్మరంధ్రాలు 40 ఉన్నాయి. గొట్టంలో ద్రవం ప్రవాహ వడి 1.5 m min^-1 అయితే రంధ్రాలనుంచి విరజిమ్మే ద్రవం వడి ఎంత?
సాధన:
గొట్టం అడ్డుకోత వైశాల్యం a₁ = 8.0cm²
8 × 10^-4 m²
రంధ్రాల సంఖ్య = 40;
ప్రతి రంధ్రం వ్యాసం D = 1m.m = 10^-3m
రంధ్రం వ్యాసార్థం, r = \(\frac{D}{2}=\frac{1}{2}\) × 10^-3m²
= 5 × 10^-3m
ప్రతిరంధ్రం అడ్డుకోత వైశాల్యం = πr²
= π(5 × 10^-4)²m²

40 రంధ్రాల అడ్డుకోత వైశాల్యం,
a₂ = 40 × π (5 × 10^-4)²m²

గొట్టంలో ద్రవవేగం, V₁ = 1.5m/min = \(\frac{1.5}{60}\)ms^-1
రంధ్రాల నుండి బయటకు వచ్చేద్రవవేగం V₂ అయితే

ప్రశ్న 17.
ఒక U-ఆకార తీగను సబ్బు ద్రావణంలో ముంచి తీస్తే తీగకు, తీగపై జారే మరొక తీగకు మధ్య. ఒక సబ్బు పొర ఏర్పడుతుంది. U-ఆకారం తీగకు దానిపై జారుతున్న తేలికైన తీగకు మధ్య ఏర్పడిన పలుచని సబ్బుపొర 1.5 × 10^-2 N (జారుడు తీగ( slider) స్వల్ప భారం కూడా ఇందులో కలిసి ఉంది). భారాన్ని మోయ గలుగుతుంది. జారుడు తీగ పొడవు 30 cm. పొర తలతన్యత ఎంత?
సాధన:
సబ్బు నీటిపొర రెండు తలాలను కలిగి ఉంటుంది, కాబట్టి పొర యొక్క మొత్తం పొడవు
= 2l = 2 × 30 = 60 cm = 0.6 m

తలతన్యత వల్ల స్లైడర్పై మొత్తం బలం,
F = S × 2l = S × 0.6 N
సమతా స్థితి వద్ద, తలతన్యత వల్ల స్లైడర్పై పనిచేసే బలం, భారం mgకి సమానం.
= (1.5 × 10^-2N)
F = 1.5 × 10^-2 = S × 0.6
S = \(\frac{1.5 \times 10^{-2}}{0.6}\) = 2.5 × 10^-2Nm^-1

ప్రశ్న 18.
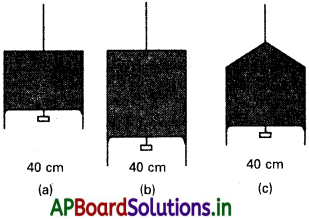
పటం 11.24 (a) లో చూపించిన ద్రవపొర 4.5 × 10^-2 N స్వల్ప భారాన్ని మోయగలదు. పటం 11.24 (b), (c) లలో చూపించిన పొరలు అదే ద్రవంతో ఏర్పడి అంతే ఉష్ణోగ్రత వద్ద ఉన్నట్లయితే ఆ పొరలు భరించగలిగే భారం ఎంతో తెలపండి. భౌతికశాస్త్ర నియమాలను అనుసరించి మీ జవాబును వివరించండి.

సాధన:
a) ఇక్కడ పొర యొక్క పొడవు = 40cm = 0.4 m
మొత్తం బలం = 4.5 × 10^-2N
పొరకు రెండు స్వేచ్ఛా తలాలు ఉన్నాయి.
తలతన్యత S = \(\frac{4.5 \times 10^{-2}}{2 \times 0.4}\)
= 5.625 × 10^-2Nm^-1

(a), (b) మరియు (c) సందర్భాలలో ఒకే ద్రవం ఉంది మరియు ఉష్ణోగ్రత కూడా ఒకే విధంగా ఉంది. (b) మరియు (c)లలో తలతన్యత 5.625 × 10^-2 ఒకే విధంగా ఉంది. పొర యొక్క పొడవు (a) లో ఒకేవిధంగా ఉంది.

ప్రతి సందర్భంలోను మొత్తం భారం 4.5 × 10^-2 N.

ప్రశ్న 19.
గది ఉష్ణోగ్రత వద్ద ఉన్న 3.00 mm వ్యాసార్ధం గల పాదరస బిందువు లోపల ఉండే పీడనం ఎంత ? ఆ ఉష్ణోగ్రత (20°C) వద్ద పాదరసం తలతన్యత 4.65 × 10^-1 Nm^-1. వాతావరణ పీడనం 1.01 × 10⁵Pa. పాదరస బిందువు లోపల ఉండే అదనపు పీడనం విలువను కూడా తెలపండి.
సాధన:
ఇక్కడ r = 3.0 mm 3 × 10^-3 m;
S = 4.65 × 10^-1Nm^-1:
P = 1.01 × 10⁵ Pa
పాదరసం లోపల అధిక పీడనం

ప్రశ్న 20.
గది ఉష్ణోగ్రత (20°C) వద్ద సబ్బు ద్రావణం తలతన్యత 2.50 × 10^-2 Nm^-1 అని ఇచ్చినప్పుడు, 5.00 mm వ్యాసార్థం గల సబ్బు ద్రావణపు బుడగ లోపల ఉండే అదనపు పీడనాన్ని లెక్కించండి. అంతే పరిమాణం లేదా అవే కొలతలు ఉన్న ఒక గాలి బుడగ ఒక పాత్రలో ఉన్న సబ్బు ద్రావణంలో 40.0 cm లోతున ఉంటే, ఆ బుడగ అంతర్భాగంలోని అదనపు పీడనం ఎంత ? సబ్బు ద్రావణం సాపేక్ష సాంద్రత =1.20. ఒక వాతావరణ పీడనం = 1.01 × 1⁵ Pa.
సాధన:
S = 2.5 x 10^-2 Nm^-1,
r = 5.00 mm
= 5 × 10^-3 m

సబ్బు ద్రావణం సాంద్రత ρ = 1.2 × 10³ kg m^-3
సబ్బు బుడగ లోపల అధిక పీడనం,

సబ్బుద్రావణంలో h లోతున ఉన్న గాలి బుడగ లోపల మొత్తం పీడనం = P’ + వాతావరణ పీడనం + hρg
= 10 + 1.01 × 10⁵ + 0.4 × 1.2 × 10³ × 9.8
= 1.06 × 10³ Pa

ప్రశ్న 21.
ఒక టాంక్ అడుగుభాగం చతురస్రాకారంలో ఉంది. ఆ అడుగు భాగం లేదా ఆధారం వైశాల్యం 1.0 m² ఈ టాంక్ మధ్యలో ఒక నిట్టనిలువు గోడను నిర్మించి దాన్ని రెండు సమాన భాగాలుగా విభజించారు. ఈ గోడ అడుగున మడతబందు సహాయంతో తిరిగే 20 cm² వైశాల్యంగల చిన్న ద్వారం ఉంది. రెండు అర్ధభాగాల్లో ఒకదానిలో నీరు మరొక దానిలో ఆమ్లం (సాపేక్ష సాంద్రత 1.7) లతో 4.0 m. ఎత్తువరకు నింపారు. ఆ ద్వారాన్ని మూసి ఉంచేందుకు అవసరమయ్యే బలాన్ని లెక్కించండి.
సాధన:
నీటిని కలిగిన గదిలో
h₁ = 4m, ρ₁ = 10³ kg m^-3

అడుగున ఉన్న తలుపుపై నీరు కలిగించే పీడనం
P₁ = h₁ρ₁g
= 4 × 10³ × 9.8
= 3.92 × 10⁴ Pa

రసాయనాన్ని కలిగిన గదిలో
h₂ = 4m, ρ₂ = 1.7 × 10³ kg/m³
అడుగున ఉన్న తలుపుపై రసాయనం కలిగించే పీడనం
P₂ = h₂ρ₂g
= 4 × 1.7 × 10³ × 9.8
= 6.664 × 10⁴ Pa
∴ పీడనంలో తేడా = P₂ – P₁
= 6.664 × 10⁴ – 3.92 × 10⁴
= 2.774 × 10⁴ Pa
తలుపు వైశాల్యం, A = 20cm² = 20 × 10^-4m²
తలుపుపై బలం = పీడనంలో తేడా × వైశాల్యం
= (P₂ – P₁) × A
= 2.774 × 10⁴ × 20 × 10⁴
= 54.88N ≈ 55N

తలుపును మూసివేయుటకు 55 N బలాన్ని క్షితిజ సమాంతరంగా నీటిని గల గది నుండి రసాయనం కలిగిన గదివైపు ప్రయోగించాలి.

ప్రశ్న 22.
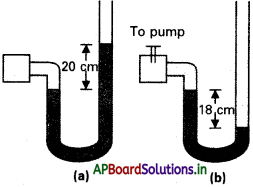
ఒక పాత్రలో బంధితమై ఉన్న వాయువు పీడనాన్ని ఒక మానోమీటర్ పటం 11.25 (a) లో చూపించిన విధంగా రీడింగ్ చూపిస్తుంది. పాత్రలోని కొంత వాయువును ఒక పంపు ద్వారా తొలగిస్తే ఉండే మానోమీటర్ రీడింగ్ను పటం 11.25 (b) సూచిస్తుంది. మనోమీటర్ లో ఉపయోగించిన ద్రవం పాదరసం అయి, వాతావరణ పీడనం 76 cm ల పాదరస స్తంభం ఎత్తుకు సమానమైతే,
a) పటం (a) పటం (b) సూచించిన రెండు సందర్భాల లోను పాత్రలోని వాయు పరమ పీడనాన్ని, గేజ్ పీడనాన్ని పాదరస cm ప్రమాణాలలో తెలపండి.
b) రెండో సందర్భంలో, అంటే పటం (b) లోని మానోమీటర్ కుడి భుజంలో 13.6 cm ఎత్తు పెరిగే విధంగా నీటిని (నీరు, పాదరసం కలవవు) నింపితే, మానోమీటర్ మట్టాలు ఏవిధంగా మారతాయి? (వాయువు ఘనపరిమాణంలో వచ్చే స్వల్ప మార్పులను ఉపేక్షించండి.

సాధన:
a) ఇక్కడ వాతావరణ పీడనం p = 76 సెం.మీ. పాదరస పీడనం
i) పటం (a) నుండి, పీడన శీర్షం
h = + 20 cm
∴ పరమ పీడనం = p + h
= 76 + 20
= 96 సెం.మీ. పాదరస పీడనం
పీడన పరిమాణం h = 20 సెంమీ. పాదరస పీడనం
పటం (b) నుండి, పీడన శీర్షం, h = -18 cm
పరమ పీడనం = p+h
= 76 + (-18)
= 58 సెం.మీ. పాదరస పీడనం

పీడన పరిమాణం = h = -18 సెంమీ. పాదరస పీడనం

ii) 13.6 సెం.మీ. నీటిని కుడిభుజంలో పోస్తే దానికి తుల్యమైనది \(\frac{13.6}{13.6}\)
h¹ = 1 సెం.మీ. పాదరస పీడనం
A వద్ద పీడనం, P_A = P + h¹ = 76 + 1 = 77 cm

రెండు భుజాలలో పాదరస మట్టాలలో తేడా h₁ అయిన B వద్ద పీడనం
P_B = 58 + h₁
∴ P_A = P_B
∴ 77 + 58 + h₁ (లేదా)
h₁ = 77 – 58 = 19 సెం.మీ. పాదరస పీడనం

ప్రశ్న 23.
విభిన్న ఆకారాల్లో ఉండే రెండు పాత్రల ఆధార వైశాల్యాలు సమానం. రెండు పాత్రల్లోను ఒక నిర్ణీత సమాన ఎత్తువరకు నీటిని నింపాలంటే మొదటి పాత్ర తీసుకొనే నీటి ఘనపరిమాణం రెండో పాత్ర తీసుకొనే నీటి ఘనపరిమాణానికి రెట్టింపు. అయితే నీరు పాత్ర ఆధారంపై ప్రయోగించే బలం రెండు సందర్భాల్లోను సమానంగానే ఉంటుందా? ఒకవేళ అలా సమానమైతే, సమాన మట్టాల వరకు నీటితో నింపిన ఆ పాత్రలు బరువు తూచే పరికరంపై రెండు వేరువేరు రీడింగులను ఎందుకు చూపిస్తాయి?
సాధన:

పీడనం నీటి స్తంభం ఎత్తుపై ఆధారపడుతుంది. మరియు వేరువేరు ఆకారాలు గల రెండు పాత్రలలో నీటి స్తంభం ఎత్తు ఒకేవిధంగా ఉంటుంది. ప్రతిపాత్ర అడుగున నీటి వలన పీడనం ఒకే విధంగా ఉంటుంది. ప్రతి పాత్ర అడుగున వైశాల్యం ఒకేవిధంగా ఉంటే, నీటి పీడనం వలన పాత్రల అడుగున వైశాల్యంపై సమాన బలాలు పని చేస్తాయి. నీరు గోడలపై కలిగించే బలం కూడా సమానం. పాత్ర గోడలు అడుగున లంబంగా లేకపోతే, నీరు గోడలపై కలిగించే బలం యొక్క ఫలిత క్షితిజ లంబ అంశం, రెండవ పాత్రలో కన్నా మొదటి పాత్రలో అధికం. ఈ విధంగా రెండు పాత్రలలో ఒకే ఎత్తున నీటిని నింపితే బరువు తూచే యంత్రంపై వేరువేరు రీడింగ్లను చూపుతాయి.

ప్రశ్న 24.
రక్తమార్పిడి చేస్తున్నప్పుడు సూదిని సిరలోకి (రక్తనాళంలోకి) గుచ్చారు. అక్కడ గేజ్ పీడనం 2000 Pa. అప్పుడు ఈ సిరలోకి రక్తం ఎక్కాలంటే రక్తం ఉండే సీసాను ఎంత ఎత్తులో అమర్చాలి?
సాధన:

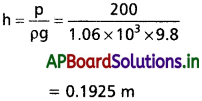
రక్తం కలిగిన పాత్ర 0.1925 m (0.2 m) ఎత్తులో ఉంటే, రక్తం నరాలలోకి ఎక్కుతుంది.

ప్రశ్న 25.
బెర్నౌలీ సమీకరణాన్ని ఉత్పాదించేటప్పుడు గొట్టంలోని ప్రవాహిపై జరిగిన పనిని ప్రవాహి స్థితిజ, గతిజ శక్తులలోని వ్యత్యాసానికి సమానం చేశాం.
a) 2 × 10^-3 m వ్యాసం గల ధమనిలో రక్త ప్రవాహం స్తరీయంగా కొనసాగేందుకు రక్తానికి ఉండాల్సిన గరిష్ఠ సగటు వేగం ఎంత?
b) ప్రవాహి వేగం పెరిగే కొద్దీ దుర్వ్యయ బలాల ప్రాముఖ్యత పెరుగుతుందా? గుణాత్మకంగా చర్చించండి.
సాధన:
a) చెదరగొట్టబడిన బలాలు పని చేస్తున్నప్పుడు, పీడనాలలో తేడావల్ల ప్రవహించే ద్రవం, కొంత బలం, ఈ బలాలకు వ్యతిరేకంగా పనిచేస్తాయి. అందువల్ల కోల్పోయే పీడనం అధికం.

b) చెదరగొట్టే బలాలు, సంక్షోభ ప్రవాహంలో ద్రవవేగాన్ని పెంచడానికి చాలా ప్రాముఖ్యత వహిస్తాయి.

ప్రశ్న 26.
a) 2 × 10^-3 m వ్యాసంగల ధమనిలోని రక్త ప్రవాహం స్తరీయంగా కొనసాగేందుకు రక్తం కలిగి ఉండాల్సిన గరిష్ఠ సగటు వేగం ఎంత?
సాధన:
ఇక్కడ r = 2 × 10^-3m ;
D = 2r= 2 × 2 × 10^-3 = 4 × 10^-3m
η = 2.084 × 10^-3 Pa – s;
p = 1.06 × 10³ kgm^-3
స్తరీయ ప్రవాహంలో, N_R = 2000

a) ఇప్పుడు V_c =

b) సంబంధిత రక్త ప్రవాహరేటు ఎంత? (రక్తం స్నిగ్ధతను 2.084 × 10^-3 Pa s గా తీసుకోండి).
సాధన:
సెకనుకు ప్రవహించే ఘనపరిమాణం = πr²V_c
= \(\frac{22}{7}\) × (2 × 10^-3)² × 0.98
= 1.23 × 10^-5 m³s^-1

ప్రశ్న 27.
ఒకొక్కటి 25m². వైశాల్యంగల రెండు రెక్కలను కలిగి ఉండే విమానం ఒక నిర్ణీత ఎత్తువద్ద స్థిరవడితో ప్రయాణిస్తున్నది. రెక్క అడుగు తలంపై గాలివేగం 180 km/h, రెక్కపై తలంపై ఉన్న గాలివేగం 234 km/h అయితే విమానం ద్రవ్యరాశిని నిర్ధారించండి. (గాలి సాంద్రతను 1 kg m^-3 గా తీసుకోండి).
సాధన:
ఇక్కడ V₁ = 180 km/h = 50m/s,
V₂ = 234 km/s = 65 m/s;
A = 2 × 25 = 50m²; p = 1 kg/m³

ప్రశ్న 28.
మిల్లికాన్ తైల బిందు ప్రయోగంలో 2.0 × 10^-5 m వ్యాసార్ధం, 1.2 × 10³ kg m^-3 సాంద్రత గల తటస్థ బిందువు (అనావేశిత బిందువు) (uncharged particle) చరమవేగం ఎంత? ప్రయోగ ఉష్ణోగ్రత వద్ద గాలి స్నిగ్ధతను 1.8 × 10^-5 Pa s గా తీసుకోండి. ఆ చరమవేగం వద్ద బిందువుపై పనిచేసే స్నిగ్ధతాబలం ఎంత? గాలివల్ల బిందువుపై పనిచేసే ఉత్సవన బలాన్ని ఉపేక్షించండి.
సాధన:
ఇక్కడ r = 2.0 × 10^-5 m;
ρ = 1.2 × 10³kgm^-3; η = 1.8 × 10^-5 Ns m^-2
P_o = 0, V = ?, F = ?

5.8 × 10^-2ms^-1 5.8 cms^-1
బిందువుపై స్నిగ్ధతా బలం, F = 6πηrv
= 6 × \(\frac{22}{7}\) × 1.8 × 10^-5 × 2.0 × 10^-5 × 5.8 × 10^-2
= 3.93 × 10^-10N.

ప్రశ్న 29.
సోడాలైమ్ గాజుతో పాదరస స్పర్శకోణం 140°. ఈ రకమైన గాజుతో చేసిన 1.00 mm వ్యాసార్ధం గల సన్నని గొట్టాన్ని పాదరసం ఉండే తొట్టెలో నిలువుగా ముంచారు. పాత్రలోని పాదరస ద్రవమట్టానికి సాపేక్షంగా నాళంలోని పాదరస మట్టం ఎంత కిందికి దిగుతుంది? ప్రయోగ ఉష్ణోగ్రత వద్ద పాదరసం తలతన్యత 0.465 Nm^-1. పాదరస సాంద్రత = 1.36 × 10³ kg m^-3.
సాధన:
ఇక్కడ θ = 140°, r = 1 × 10^-3 m;
S = 0.465 Nm^-1, ρ = 13.6 × 10³ kg, h = ?]
cos = 140° = – cos40° = -0.7660

ఇక్కడ ఋణగుర్తు గొట్టంలో పాదరస మట్టం పడిపోవుటను సూచిస్తుంది.

ప్రశ్న 30.
3.0 mm, 6.0 mm వ్యాసాలున్న రెండు సన్నని నాళాలను కలిపి రెండు చివరలలో తెరచి ఉంచిన U- ఆకార గొట్టాన్ని తయారుచేశారు. U-గొట్టంలోని నీటిని కలిగి ఉంటే, గొట్టంలోని రెండు భుజాల్లోని నీటి మట్టాల్లోని వ్యత్యాసం ఎంత? ప్రయోగ ఉష్ణోగ్రత వద్ద నీటి తలతన్యత 7.3 × 10^-2 N m^-1. స్పర్శకోణాన్ని శూన్యంగా, నీటి సాంద్రతను 1.0 × 10³ kg m^-3గా తీసుకోండి ( g = 9.8 m^-2).
సాధన:
S = 7.3 × 10^-2 Nm^-1,
ρ = 1.0 × 10³ kg m^-3; θ = 0°
సన్నని గొట్టంలో, 2r_{1/sub> = 3.00 m.m = 3 × 10^-3 m
(లేదా) r1 = 1.5 × 10^-3 m}

వెడల్పు గొట్టంలో, 2r₂ = 6.00 m.m (లేదా) = 3 × 10^-3 m
= 6 × 10^-3 m

సన్నని గొట్టం మరియు వెడల్పు గొట్టంలో నీటి ఎత్తులు h₁, h₂ అనుకొనుము.

ప్రశ్న 31.
a) ఎత్తు తో గాలి సాంద్రత తగ్గడాన్ని ρ = ρ_oe^-y/y_o సమీకరణం సూచిస్తుంది.
ఇక్కడ ρ_o సముద్ర మట్టం వద్ద గాలి సాంద్రత = 1.25 kg m^-3y₀ = స్థిరాంకం. వాతావరణ సాంద్రతలో వచ్చే మార్పులను తెలిపే ఈ సమీకరణాన్నే వాతవరణాల నియమం (law of atmospheres) అంటారు. వాతావరణ ఉష్ణోగ్రత స్థిరంగా (సమోష్ణోగ్రతా పరిస్థితులు) ఉందని భావించి ఈ నియమాన్ని రాబట్టండి. g విలువ కూడా స్థిరమని భావించండి.
సాధన:
సాంద్రతలో తగ్గుదల రేటు, ρ ఎత్తు y కు అనులోమాను పాతంలో ఉంటుంది.
\(\frac{-\mathrm{d} \rho}{\mathrm{dy}}\) α ρ (లేదా) \(\frac{\mathrm{d} \rho}{\mathrm{dy}}\) = – Kρ

ఇక్కడ K అనుపాత స్థిరాంకం. ఇక్కడ ఋణగుర్తు ρ తగ్గితే, y పెరుగుతుందని తెలియజేస్తుంది.

b) 1425 m³ ఘనపరిమాణం గల ఒక హీలియం బెలూన్ను ఉపయోగించి 400 kg భారాన్ని (pay load) పైకి ఎత్తుతున్నారు. బెలూన్ పైకి వెళుతున్న కొద్దీ దాని వ్యాసార్ధం స్థిరంగానే ఉంటుందని భావించి అది చేరే ఎత్తును లెక్కించండి.
(y_o = 8000 m and P_He = 0.18 kgm^-3 అని తీసుకోండి).
సాధన:
బెలూన్ ఎత్తుకు పోయేసరికి దాని సాంద్రత, ఆ ఎత్తులో గాలికి సమానం.

సాధించిన సమస్యలు (Solved Problems)

ప్రశ్న 1.
ఒక్కొక్కటి 10 cm² మధ్యచ్ఛేద వైశాల్యం కలిగిన రెండు తొడ ఎముకలు (femurs), 40 kg ద్రవ్యరాశి గల మానవ శరీర పైభాగాన్ని మోస్తున్నాయి అనుకొందాం. ఈ తుంటి ఎముకలు తట్టుకో గలిగే సగటు పీడనాన్ని అంచనావేయండి.
సాధన:
తుంటి ఎముకల మొత్తం మధ్యచ్ఛేద వైశాల్యం A = 2 × 10cm² 20 × 10^-4m². (g 10 ms^-2) గా తీసుకొంటే వాటిపై చర్య జరిపే బలం F = 40 kg wt = 400 N. ఈ బలం నిలువుగా కిందివైపుకు పనిచేస్తుంది. కాబట్టి ఈ బలం తుంటి ఎముకలపై అభిలంబంగా ఉంటుంది. కాబట్టి సగటు పీడనం
P_av = \(\frac{F}{A}\) = 2 × 10⁵ N m^-2

ప్రశ్న 2.
ఒక సరస్సు ఉపరితలం నుంచి 10m లోతున ఉన్న ఈతగాడిపై ఎంత పీడనం ఉంటుంది?
సాధన:
ఇక్కడ
h = 10 m, ρ = 1000 kg m^-3 కాగా
g = 10 m S^-2 గా తీసుకోండి.
సమీకరణం (11.7b) నుంచి
P = P_a +ρgh
= 1.01 × 10⁵ Pa + 1000 kgm^-3 × 10m S^-2 × 10 m
= 2.01 × 10⁵ Pa
≈ 2 atm

ఉపరితల మట్టం వద్ద ఉండే పీడనం నుంచి, ఈ పీడనం 100% పెరుగుదల సూచిస్తోంది. 1 km లోతులో పీడనం పెరుగుదల 100 atm! ఇలాంటి విపరీతమైన వీడనాల్ని తట్టుకొనేటట్టుగా జలాంతర్గాములను రూపొందిస్తారు.

ప్రశ్న 3.
సముద్రమట్టం వద్ద వాతావరణ సాంద్రత 1.29 kg/m³. ఇది ఉన్నతి (ఎత్తు)తో మారడం లేదని అనుకోండి. అయితే ఎంత ఎత్తు వరకు వాతావరణం వ్యాపించి ఉంటుంది?
సాధన:
సమీకరణం (11.7a) నుంచి
ρgh = 1.29 kg m^-3 × 9.8 ms² × hm
= 1.01 × 10⁵ pa
∴ h = 7989 m ≈ 8 km

నిజానికి గాలి సాంద్రత ఎత్తుకు వెళ్ళేకొలది తగ్గుతుంది. అదే విధంగా g కూడా. వాతావరణ పొర తగ్గుతూ ఉండే పీడనం కలిగి 100 km వరకు విస్తరించి ఉంటుంది. సముద్రమట్టం వద్ద వాతావరణ పీడనం ఎప్పుడూ 760 mm of Hg గానే ఉండదని మనం గుర్తించాలి. పాదరస మట్టం, 10 mm of Hg లేదా అంతకంటే ఎక్కువగా పడిపోయినట్లయితే అది రాబోయే తుఫానును సూచిస్తుంది.

ప్రశ్న 4.
ఒక మహాసముద్రంలో 1000 m లోతున (a) పరమపీడనం ఎంత ఉంటుంది? b) గేజ్ పీడనం ఎంత ఉంటుంది? c) అదే లోతున ఉన్నప్పుడు, 20 cm × 20 cm వైశాల్యం ఉన్న జలాంతర్గామి కిటికీపై చర్య జరిపే బలం ఎంత ? ఈ జలాంతర్గామి లోపలి వీడనాన్ని సముద్రమట్టం వద్ద ఉండే వాతావరణ పీడనానికి సమానంగా ఉండేట్లు చూస్తారు. (సముద్ర జలం సాంద్రత 1.03 × 10³ kg m^-3, g = 10ms^-2.)
సాధన:
ఇక్కడ h = 1000, ρ = 1.03 × 10³ kg m^-3

a) సమీకరణం(11.6)ను బట్టి పరమ పీడనం
P = P_a + ρgh
= 1.01 × 10⁵ Pa
+ 1.03 × 10³ kg m^-3 ×10m s^-2 × 1000 m
= 104.01 × 10⁵ Pa
≈ 104 atm

b) గేజ్ పీడనం P – P_a = ρgh = P_g
P_g = 1.03 × 10³ kg m^-3 × 10 m s² × 1000 m
= 103 × 10⁵ Pa
≈ 103 atm

c) జలాంతర్గామి బయట ఉండే పీడనం, P = P_a + ρgh దాని లోపలి పీడనం P_a. అందువల్ల, జలాంతర్గామి కిటికీ మీద చర్య జరిపే నికర పీడనం గేజ్ పీడనమే; గేజ్ పీడనం P_g = ρgh. కీటికీ వైశాల్యం A = 0.04 m², కాబట్టి దానిపై పనిచేసే బలం F అయితే,
F = P_g A = 103 × 10⁵ Pa × 0.04m²
= 4.12 × 10⁵ N.

ప్రశ్న 5.
A₁, A₂ అనే వేరువేరు మధ్యచ్ఛేద వైశాల్యాలు; L₁, L₂ అనే వేరువేరు పొడవులు కలిగి నీటితో నింపిన రెండు. (సూదులు లేని) సిరంజిలను బాగా బిగుతుగా ఉండి, నీటితో నింపిన రబ్బరు గొట్టానికి కలిపారు. వాటి చిన్న ముషలకం, పెద్ద ముషలకాల వ్యాసాలు వరసగా 1.0 cm, 3.0 cm లు.
a) చిన్న ముషలకానికి 10 N బలాన్ని అనువర్తింపచేసినప్పుడు, పెద్ద ముషలకంపై కలిగే బలం ఎంత?
b) చిన్న ముషలకాన్ని 6.0 cm దూరం లోపలికి నెట్టితే పెద్ద ముషలకం ఎంత దూరం బయటివైపుకు కదులుతుంది?
సాధన:
a) ప్రవాహి అంతటా పీడనం ఏమాత్రం క్షీణించకుండా ప్రసరితమవుతుంది కాబట్టి,

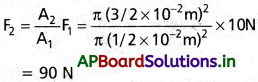
b) నీటిని ఒక సంపూర్ణ అసంపీడ్య ప్రవాహిగా భావిస్తాం. చిన్న ముషలకాన్ని లోపలకు నెట్టడం వల్ల కదిలిన నీటి మనపరిమాణం పెద్ద ముషలకం వల్ల బయటివైపుకు కదిలిన నీటి ఘనపరిమాణానికి సమానం.

రెండు ముషలకాలపైన పనిచేసే వాతావరణ పీడనం ఒకటే కాబట్టి దానిని మనం పట్టించుకోలేదని గమనించండి.

ప్రశ్న 6.
ఒక కారు లిఫ్ట్ సంపీడిత గాలి (compressed air) 5.0 cm వ్యాసార్ధం గల చిన్న ముషలకంపై F₁ బలాన్ని కలిగిస్తుంది. ఈ పీడనం 15 cm వ్యాసార్ధం గల రెండవ ముషలకానికి ప్రసరిత మవుతుంది (పటం. 11.6). పైకి లేవనెత్తాల్సిన కారు యొక్క ద్రవ్యరాశి 1350 kg లు అయితే, F₁ ను లెక్కగట్టండి. ఈ కష్టతర కార్యాన్ని సుసాధ్యం చేయడానికి అవసరమయ్యే పీడనం ఎంత ? (g = 9.8 ms^-2).

సాధన:
ప్రవాహి అంతటా ఏమాత్రం క్షీణించకుండా పీడనం ప్రసరితమవుతంది కాబట్టి.

ఈ బటాన్ని ఉత్పత్తి చేసే గాలి పీడనం.

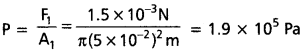
ఇది వాతావరణ పీడనానికి దాదాపు రెట్టింపు. ఆటోమొబైల్లోని హైడ్రాలిక్ బ్రేక్లు కూడా ఇదే (పాస్కల్) సూత్రంపై ఆధారపడి పనిచేస్తాయి.

మన పాదంతో పెడల్పైన మనం ఒక స్వల్ప బలాన్ని ప్రయోగిస్తే, మాస్టర్ స్థూపంలోని (master cylinder) మాస్టర్ ముషలకం కదులుతుంది. ఇందువల్ల కలిగే పీడనం బ్రేక్ నూనె ద్వారా ప్రసరితమై దీనికంటే ఎక్కువ వైశాల్యం గల ముషలకంపైన చర్య జరుపుతుంది. ఇందువల్ల ఒక అత్యధిక బలం ఆ ముషలకంపై చర్య జరిపి, అది కిందకు నెట్టబడుతుంది. తద్వారా బ్రేక్ లైనింగ్కు వ్యతిరేకంగా బ్రేకులు వ్యాకోచం చెంది, అంటే అవి ముందుకు జరిగి, బ్రేక్ లైనింగ్ను గట్టిగా ఒడిసిపట్టుకొంటాయి. ఈవిధంగా పెడల్పైన చర్యజరిపే స్వల్ప బలం, చక్రంపై అధిక మందక బలాన్ని (large retarding force) ఉత్పన్నం చేస్తుంది. ఈ వ్యవస్థలోని ఒక ముఖ్యమైన లాభమేమిటంటే, పెడల్ను నొక్కడం వల్ల ఏర్పడే పీడనం, కారు నాలుగు చక్రాలకు అనుసంధానితమై ఉన్న అన్ని స్థూపాలకు సమానంగా ప్రసరితం అయి, అన్ని చక్రాలపైన కలిగే బ్రేకింగ్ యత్నం (effort) సమానంగా ఉంటుంది.

ప్రశ్న 7.
రక్తపు వేగం : మత్తుమందిచ్చిన ఒక కుక్క యొక్క బృహద్ధమని (large artery) లోని రక్త ప్రవాహాన్ని ఒక వెంటురి మీటర్ ద్వారా వెళ్ళేటట్లుగా దారి మళ్లించారు. ఈ మీటర్ యొక్క వెడల్పాటి భాగం యొక్క మధ్యచ్ఛేద వైశాల్యం ధమని మధ్యచ్ఛేద వైశాల్యంA కి సమానం A = 8 mm². ఇక దాని ఇరుకైన భాగం యొక్క మధ్యచ్ఛేద వైశాల్యం a = 4mm². ధమనిలో పీడన పతనం (pressure drop) 24 Pa ఉంది. ధమనిలో రక్తం ఎంత వడితో ప్రవహిస్తుంది?
సాధన:
పట్టిక 11.1 నుంచి రక్తం సాంద్రతను 1.06 × 10³ kg m^-3 గా తీసుకొందాం. మధ్యచ్ఛేద వైశాల్యాల నిష్పత్తి,

ప్రశ్న 8.
ప్రయాణికులతో పూర్తిగా నిండిన ఒక బోయింగ్ విమానం ద్రవ్యరాశి 3.3 × 10⁵ kg. దాని రెక్కల మొత్తం వైశాల్యం 500 m². అది 960 km/h. వడితో ఒకే స్థాయిలో ఎగురుతున్నది. a) రెక్కల కింది, పై ఉపరితలాల మధ్య ఉన్న పీడన వ్యత్యాసాన్ని అంచనా వేయండి. (b) రెక్క కింది ఉపరితలానికి సాపేక్షంగా, రెక్కపై భాగపు ఉపరితలం మీద ఉండే గాలి వడిలో అంశిక పెరుగుదలను అంచనా వేయండి. [గాలి సాంద్రత p = 1.2 kgm^-3].
సాధన:
a) పీడన వ్యత్యాసం మూలంగా జనించిన అధోబలం బోయింగ్ విమానం బరువును సంతులనం చేస్తుంది.
∆P × A = 3.3 × 10⁵ kg × 9.8 = mg.
ΔΡ = (3.3 × 10⁵ kg × 9.8 m s^-2) / 500 m²
= 6.5 × 10³ N m^-2

b) రెక్క పైభాగానికీ, కింది భాగానికీ మధ్య ఉండే ఎత్తులోని స్వల్ప భేదాన్ని మనం వదిలివేయవచ్చు. అప్పుడు వాటి మధ్య పీడన వ్యత్యాసం

రెక్క పైభాగంలో ఉండే గాలి వడి, కింది భాగంలో ఉండే గాలి వడి కంటే కేవలం 8% మాత్రమే ఎక్కువగా ఉండాల్సి ఉంటుంది.

ప్రశ్న 9.
పటంలో చూపించిన విధంగా 0.10 m² వైశాల్యం గల ఒక లోహదిమ్మెను ఒక ఆదర్శ కప్పీ (ద్రవ్యరాశిరహిత, ఘర్షణ రహిత కప్పీ) ద్వారా పోయే ఒక తాడు సహాయంతో 0.010 kg ద్రవ్యరాశితో అనుసంధానించారు. 0.30 mm పొర మందం (film thickness) గల ఒక ద్రవాన్ని బల్లకూ, దిమ్మెకూ మధ్య ఉంచారు. స్వేచ్ఛగా వదిలిపెడితే, దిమ్మె 0.085ms^-1 స్థిరమైన వడితో కుడివైపుకు కదులుతుంది. ఆ ద్రవం స్నిగ్ధతా గుణకాన్ని కనుక్కోండి.

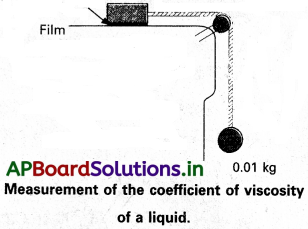
సాధన:
తాడులోని తన్యత మూలంగా లోహ దిమ్మె కుడివైపుకు కదులుతుంది. తన్యత T అనేది వేలాడదీసిన ద్రవ్యరాశి m యొక్క భారానికి పరిమాణంలో సమానంగా ఉంటుంది. కాబట్టి విరూపణ బలం,
F = T = mg = 0.010 kg × 9.8 ms^-2
= 9.8 × 10^-2 N
ఆ ప్రవాహిపై విరూపణ ప్రతిబలం

ప్రశ్న 10.
ఒక టాంక్లో 20°C వద్ద ఉన్న నూనె ద్వారా కిందకు పడుతున్న 2.0 mm వ్యాసార్ధం గల ఒక రాగి బంతి చరమవేగం 6.5 cm s^-1.20°C వద్ద నూనెకు ఉండే స్నిగ్ధతా గుణకాన్ని గణించండి. నూనె సాంద్రత 1.5 × 10³ kg m^-3, రాగి సాంద్రత 8.9 × 10³ kg m^-3.
సాధన:
దత్తాంశం ప్రకారం v_t = 6.5 × 10^-2 ms^-1
a = 2 × 10^-3m,
g = 9.8 ms^-2
ρ = 8.9 × 10³ kg m^-3,
σ = 1.5 × 10³ kg m^-3.
సమీకరణం (11.20) ప్రకారం,

ప్రశ్న 11.
a) 1.25 cm వ్యాసం గల ఒక కుళాయి నుంచి వస్తున్న నీటి ప్రవాహరేటు 0.48 L/min. నీటిస్నిగ్ధతా గుణకం 10^-3 Pa s.
b) కాసేపటి తరవాత ప్రవాహ రేటును 3L/min.కు పెంచడం జరిగింది. ఈ రెండు ప్రవాహ రేట్లకు సంబంధించిన ప్రవాహాన్ని అభిలక్షణీకరించండి.
సాధన:
a) ప్రవాహ వడి అనుకొందాం. కుళాయి వ్యాసం
d 1.25 cm. ఒక సెకనుకు ప్రవహించే నీటి ఘనపరిమాణం
Q = v × πd²/4
v = 4Q / d² π

ఇప్పుడు రెనాల్డ్స్ సంఖ్యను అంచనా వేయవచ్చు.
R_e = 4ρQ / 7dm
= 4 × 10³ kg m^-3 × Q/
(3.14 × 1.25 × 10^-2 m × 10^-3 PaS)
= 1.019 × 10⁸ m^-3 SQ

తొలుతగా (a)
Q = 0.48 L/min 8 cm³ / s
= 8 × 10^-6 m³s^-1,

కాబట్టి, మనకు R_e = 815 అని వస్తుంది

ఈ విలువ 1000 కంటే తక్కువగా ఉంది కాబట్టి ఈ ప్రవాహం నిలకడ ప్రవాహం.

కొంతసేపటి తరవాత (b)
Q = 3L/min = 50 cm³
s = 5 × 10^-5 m³ s^-1

అయినప్పుడు
R_e = 5095 అని వస్తుంది.

ఇక్కడ, అంటే సందర్భం (b) కి, ప్రవాహం సంక్షుభితమై ఉంటుంది. మీరు మీ ‘వాష్ బేసిన్’లో ఒక ప్రయోగం చేసి చూడటం ద్వారా స్తరీయ ప్రవాహం నుంచి సంక్షుబ్ధ ప్రవాహంగా సంక్రమణం చెందడాన్ని గమనించ వచ్చు.

ప్రశ్న 12.
2.00 mm వ్యాసమున్న కేశనాళిక కింది కొనను ఒక బీకరులోని నీటి ఉపరితలానికి 8.00 cm దిగువ వరకు ముంచారు. నీటిలో మునిగి ఉన్న కొన వద్ద ఒక అర్థగోళాకార బుడగ ఏర్పడేటట్లుగా ఊదడానికి నాళికలో అవసరమయ్యే పీడనం ఎంత? ప్రయోగాన్ని నిర్వహిస్తున్న ఉష్ణోగ్రత వద్ద నీటి తలతన్యత 7.30 × 10^-2 Nm¹, 1 అట్మాస్ఫియరిక్ పీడనం = 1.01 × 10⁵ Pa, నీటి సాంద్రత = 1000kg/m³,
g = 9.8 × ms^-2.
ఇందులో అదనపు పీడనాన్ని కూడా లెక్కించండి.
సాధన:
ఒక ద్రవంలో ఏర్పడే వాయు బుడగలో అదనపు పీడనం 2S/r. ఇక్కడ ఓ అనేది ద్రవ-వాయు ఉమ్మడి తలం యొక్క తలతన్యత. ఈ సందర్భంలో కేవలం ఒక ద్రవ ఉపరితలం మాత్రమే ఉందని మీరు గమనించాలి. (ఒక వాయువులో ఏర్పడే ద్రవపు బుడగ విషయంలో రెండు ద్రవ ఉపరి తలాలు ఉంటాయి. కాబట్టి ఈ సందర్భంలో అదనపు పీడనం 45 / r.) నీటిలో ఏర్పడే బుడగ వ్యాసార్ధం r. నీటిలోపల బుడగ బయట ఉండే పీడనం, P_o అనుకొంటే, ఈ P_o అనేది వాతావరణ పీడనం, 8.00 cm ల నీటిస్తంభం (ఈ రెండింటి) వల్ల కలిగే పీడనాల మొత్తానికి సమానమవుతుంది. అంటే,
P_o = (1.01 × 10⁵ Pa + 0.08 m × 1000 kg m^-3 × 9.80 m s^-2)
= 1.01784 × 10⁵ Pa

అందువల్ల, బుడగ లోపలి పీడనం P₁ = P₀ + 2S / r ( r = 1 mm కాబట్టి)
= 1.01784 × 10⁵ Pa +
(2 × 7.3 × 10^-2 Pa m/ 10^-3 m)
= (1.01784 + 0.00146) × 10⁵ Pa
= 1.02 × 10⁵ Pa

ఇక్కడ బుడగ అర్థగోళాకృతిలో ఉన్నందువల్ల దాని వ్యాసార్ధాన్ని కేశనాళిక వ్యాసార్ధానికి సమానంగా తీసుకోవడమైంది.