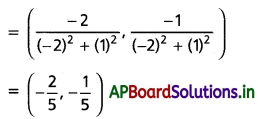Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 1 సంకీర్ణ సంఖ్యలు Exercise 1(a) will help students to clear their doubts quickly.
AP Inter 2nd Year Maths 2A Solutions Chapter 1 సంకీర్ణ సంఖ్యలు Exercise 1(a)
అభ్యాసం 1(ఎ)
I.
ప్రశ్న 1.
z1 = (2, -1), z2 = (6, 3), and z1 – z2 ను కనుక్కోండి.
సాధన:
∵ z1 = (2, -1), z2 = (6, 3)
z1 – z2 = (2 – 6, -1 – 3) = (-4, -4)
ప్రశ్న 2.
z1 = (3, 5), z2 = (2, 6) అయితే z1 . z2 ను కనుక్కోండి.
సాధన:
z1 = (3, 5) = 3 + 5i
z2 = (2, 6) = 2 + 6i
z1 . z2 = (3 + 5i) . (2 + 6i)
= 6 + 10 + 18i + 30i2 (∵ i2 = -1)
= 6 + 28i + 30(-1)
= -24 + 28i
= (-24, 28)
![]()
ప్రశ్న 3.
క్రింది సంకీర్ణ సంఖ్యల సంకలన విలోమాన్ని వ్రాయండి.
(i) (√3, 5)
(ii) (-6, 5) + (10, -4)
(iii) (2, 1) (-4, 6)
సాధన:
(a, b) కు సంకలన విలోమం (-a, -b) కనుక
(i) (√3, 5)
సంకీర్ణ సంఖ్యకు సంకలన విలోమం (√3, -5)
(ii) (-6, 5) + (10, -4)
= (-6 + 10, 5 + (-4))
= (4, 1)
∴ సంకలన విలోమం (-4, -1)
(iii) (2, 1) . (-4, 6)
= ((2 × -4 – 1 × 6), (1 × -4 + 2 × 6))
= (-8 – 6, -4 + 12)
= (-14, 8)
∴ సంకలన విలోమం (14, -8)
II.
ప్రశ్న 1.
z1 = (6, 3); z2 = (2, -1) అయితే z1/z2 ని కనుక్కోండి.
సాధన:
∵ z1 = (6, 3) = 6 + 3i
z2 = (2, -1) = 2 – i

ప్రశ్న 2.
z = (cos θ, sin θ) అయితే (z – \(\frac{1}{z}\)) ని కనుక్కోండి.
సాధన:
∵ z = (cos θ, sin θ) = cos θ + i sin θ
\(\frac{1}{z}\) = cos θ – i sin θ
∴ z – \(\frac{1}{z}\) = (cos θ + i sin θ) – (cos θ – i sin θ)
= 2 i sin θ
= 0 + i(2 sin θ)
= (0, 2 sin θ)
![]()
ప్రశ్న 3.
క్రింది సంకీర్ణ సంఖ్యల గుణన విలోమాన్ని వ్రాయండి.
(i) (3, 4)
(ii) (sin θ, cos θ)
(iii) (7, 24)
(iv) (-2, 1)
సాధన:
(a, b) సంకీర్ణ సంఖ్యకు గుణన విలోమం = \(\left(\frac{a}{a^2+b^2}, \frac{-b}{a^2+b^2}\right)\)
(i) (3, 4) కు గుణన విలోమం

(ii) (sin θ, cos θ) కు గుణన విలోమం
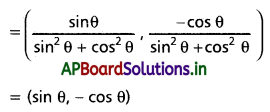
(iii) (7, 24) కు గుణన విలోమం
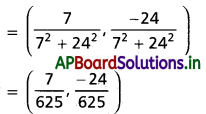
(iv) (-2, 1) కు గుణన విలోమం