Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 1 సంకీర్ణ సంఖ్యలు Exercise 1(b) will help students to clear their doubts quickly.
AP Inter 2nd Year Maths 2A Solutions Chapter 1 సంకీర్ణ సంఖ్యలు Exercise 1(b)
అభ్యాసం 1(బి)
I.
ప్రశ్న 1.
క్రింది సంకీర్ణ సంఖ్యలను a + ib రూపంలో వ్రాయండి.
(i) (2 – 3i) (3 + 4i)
సాధన:
(2 – 3i) (3+ 4i) = 6 + 8i – 9i – 12i2
= (6 + 12) – i
= 18 – i
= 18 + i(-1)
(ii) (1 + 2i)3
సాధన:
(1 + 2i)3 = 1 + 3(2i) + 3(2i)2 + (2i)3
= 1 + 6i + 3(-4) + 8i3
= 1 + 6i – 12 – 8i
= -11 – 2i
= -11 + i(-2)
(iii) \(\frac{a-i b}{a+i b}\)
సాధన:

(iv) \(\frac{4+3 i}{(2+3 i)(4-3 i)}\)
సాధన:
(2 + 3i) (4 – 3i) = 8 – 6i + 12i – 9i2 = 17 + 6i

(v) (-√3 + √-2) (2√3 – i)
సాధన:
(-√3 + √-2) (2√3 – i)
= (-√3 + i√2) (2√3 – i)
= -6 + i√3 + i 2√6 + √2
= (-6 + √2) + i(√3 + 2√6)
![]()
(vi) -5i (\(\frac{i}{8}\))
సాధన:
-5i (\(\frac{i}{8}\)) = \(\frac{-5 i^2}{8}\)
= \(\frac{5}{8}\)
= \(\frac{5}{8}\) + i(0)
(vii) (-i) (2i)
సాధన:
(-i) (2i) = -2i2
= (-2) (-1)
= 2
= 2 + i(0)
(viii) i9
సాధన:
i9 = (i8) (i)
= (i2)4 i
= (-1)4 i
= i
= 0 + i(1)
(ix) i-19
సాధన:

(x) 3(7 + 7i) + i(7 + 7i)
సాధన:
3(7 + 7i) + i(7 + 7i)
= 21 + 21i + 7i + 7i2
= 21 + 28i + 7(-1)
= 14 + 28i
= 14 + i(28)
![]()
(xi) \(\frac{2+5 i}{3-2 i}+\frac{2-5 i}{3+2 i}\)
సాధన:

ప్రశ్న 2.
క్రింది సంకీర్ణ సంఖ్యలకు సంయుగ్మాలను వ్రాయండి.
(i) 3 + 4i
సాధన:
3 + 4i కు సంయుగ్మ సంకీర్ణ సంఖ్య 3 – 4i
(ii) (15 + 3i) – (4 – 20i)
సాధన:
(15 + 3i) – (4 – 20i)
= 15 + 3i – 4 + 20i
= 11 + 23i
దాని సంయుగ్మ సంకీర్ణ సంఖ్య = 11 – 23i
(iii) (2 + 5i) (-4 + 6i)
సాధన:
(2 + 5i) (-4 + 6i)
= -8 + 12i – 20i + 30i2
= -38 – 8i
దాని సంయుగ్మ సంకీర్ణ సంఖ్య = -38 + 8i
(iv) \(\frac{5 \mathbf{i}}{\mathbf{7 + i}}\)
సాధన:

ప్రశ్న 3.
క్రింది వాటిని సూక్ష్మీకరించండి.
(i) i2 + i4 + i6 + (2n + 1) + ….. పదాల వరకు
సాధన:
i2 + i4 = -1 + (-1)2 = 0
ఇదే విధంగా i6 + i8 = (i2)3 + (i2)4
= (-1)3 + (-1)4
= -1 + 1
= 0
(i.e..) రెండు వరుస పదాల మొత్తం… = 0
∴ చివరి పదం (i2)2n+1 = (-1)2n+1 = -1
∴ i2 + i4 + i6 + …..(2n + 1) పదాలు = -1
(ii) i18 + 3 . i7 + i2 (1 + i4) (-i26)
సాధన:
i18 = i16 . i2
= (i4)4 i2
= 1(-1)
= -1
i7 = i4 . i2 . i = 1(-1) i = -i
i4 = 1
(-i)26 = i26
= i24 . i2
= (i4)6 . i2
= i6(-1)
= -1
i18 – 3i7 + i2 (1 + i4) (-i)26
= 1 – 3(-i)(-1)(1 + 1) (-1)
= -1 + 3i + 2
= 1 + 3i
![]()
ప్రశ్న 4.
క్రింది సంకీర్ణ సంఖ్యలకు వర్గమూలాలను కనుక్కోండి.
(i) 7 + 24i
సాధన:
\(\sqrt{7+24 i}\) = ±(a + ib)
ఇరువైపులా వర్గం చేయగా
7 + 24i = (a + ib)2
= a2 + i2b2 + 2iab
= a2 – b2 + 2iab
వాస్తవ, సంకీర్ణ భాగాలను పోల్చగా
a2 – b2 = 7 …….(1)
2ab = 24 ……(2)
(a2 + b2)2 = (a2 – b2)2 + 4a2b2
= 49 + 576
= 625
a2 + b2 = 25 ……(3)
a2 – b2 = 7 …….(1)
కలుపగా 2a2 = 32
⇒ a2 = 16
⇒ a = 4
తీసివేయగా 2b2 = 18
⇒ b2 = 9
⇒ b = 3
\(\sqrt{7+24 i}\) = ±(4 + 3i)
(ii) -8 – 6i
సాధన:
\(\sqrt{-8-6 i}\) = ±(a – ib) అనుకుందాం.
ఇరువైపులా వర్గం చేయగా
-8 – 6i = (a – ib)2
= a2 + i2b2 – 2iab
= a2 – b2 – 2iab
వాస్తవ, సంకీర్ణ భాగాలను పోల్చగా
a2 – b2 = -8 …..(1)
2ab = +6 …….(2)
(a2 + b2)2 = (a2 – b2)2 + 4a2b2
= 64 + 36
= 100
a2 + b2 = 10 ……(3)
a2 – b2 = -8 ……(1)
కలుపగా 2a2 = 2
⇒ a2 = 1
⇒ a = 1
తీసివేస్తే 2b2 = 18
⇒ b2 = 9
⇒ b = 3
\(\sqrt{-8-6 i}\) = (1 – 3i)
∴ -8 – 6i వర్గమూలం = ±(1 – 3i)
(iii) (3 + 4i) [Mar. ’13]
సాధన:
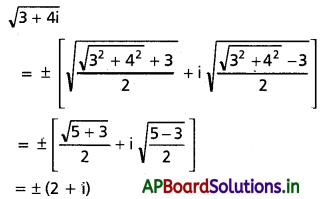
(iv) (-47 + i . 8√3)
సాధన:

![]()
ప్రశ్న 5.
క్రింది సంకీర్ణ సంఖ్యలకు గుణన విలోమాన్ని కనుక్కోండి.
(i) √5 + 3i
(ii) -i
(iii) i-35
సాధన:
∵ a + ib గుణన విలోమం \(\frac{a-i b}{a^2+b^2}\)
(i) √5 + 3i గుణన విలోమం
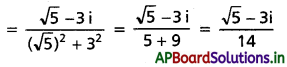
(ii) -i గుణన విలోమం = \(\frac{0+i}{1}\) = i
(iii) i-35
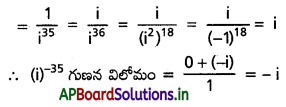
II.
ప్రశ్న 1.
(i) (a + ib)2 = x + iy అయితే x2 + y2 ను కనుక్కోండి.
సాధన:
∵ x + iy = (a + ib)2
= a2 + i2b2 + i2ab
= (a2 – b2) + i(2ab)
ఇరువైపులా వాస్తవ మరియు కల్పిత భాగాలను పోల్చగా
x = a2 – b2, y = 2ab
∴ x2 + y2 = (a2 – b2) + (2ba)2
= a4 + b4 – 2a2b2 + 4a2b2
= a4 + b4 + 2a2b2
= (a2 + b2)2
∴ x2 + y2 = (a2 + b2)2
(ii) x + iy = \(\frac{3}{2+\cos \theta+i \sin \theta}\) అయితే x2 + y2 = 4x – 3 అని చూపండి.
సాధన:

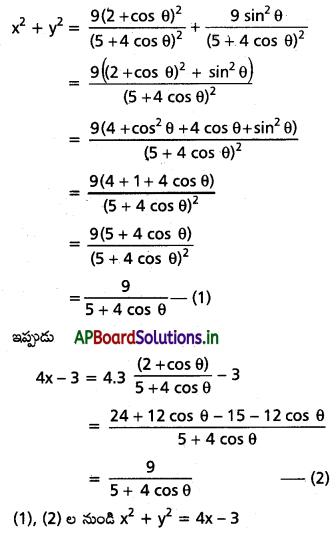
(iii) x + iy = \(\frac{1}{1+\cos \theta+i \sin \theta}\), అయితే 4x2 – 1 = 0 అని చూపండి. [A.P. Mar ’16, Mar. ’06]
సాధన:

వాస్తవ భాగాన్ని పోల్చగా x = \(\frac{1}{2}\)
⇒ 2x = 1
⇒ 4x2 = 1
⇒ 4x2 – 1 = 0
![]()
(iv) u + iv = \(\frac{2+i}{z+3}\), z = x + iy, అయితే u, v లను కనుక్కోండి.
సాధన:

ప్రశ్న 2.
(i) z = 3 – 5i అయితే, z3 – 10z2 + 58z – 136 = 0 అని చూపండి.
సాధన:
z = 3 – 5i
z – 3 = -5i
(z – 3)2 = (-5i)2
z2 – 6z + 9 = -25
z2 – 6z + 34 = 0
z3 – 10z2 + 58z – 136 = z(z2 – 6z + 34) – 4z2 + 24z – 136
= z(0) – 4(z2 – 6z + 34)
= 0 – 4(0)
= 0
∴ z3 – 10z2 + 58z – 136 = 0
(ii) z = 2 – i√7 అయితే, 3z3 – 4z2 + z + 88 = 0 అని చూపండి.
సాధన:
∵ z = 2 – i√7
z – 2 = -i√7
(z – 2)2 = (-i√7)2
z2 – 4z + 4 = 7
z2 – 4z + 11 = 0
3z3 – 4z2 + z + 88 = 3z(z2 – 4z +11) + 8z2 – 32z + 88
= 3z(0) + 8(z2 – 4z + 11)
= 0 + 8(0)
= 0
![]()
(iii) \(\frac{2-i}{(1-2 i)^2},-\left(\frac{2+11 i}{25}\right)\) లు పరస్పరం సంయుగ్మ సంకీర్ణ సంఖ్యలని చూపండి.
సాధన:

x + iy, x – iy రూపంలో ఉన్నవి.
∴ అవి పరస్పర సంయుగ్మ సంకీర్ణ సంఖ్యలు.
ప్రశ్న 3.
(i) (x – iy)1/3 = a – ib అయితే, \(\frac{x}{a}+\frac{y}{b}\) = 4(a2 – b2) అని చూపండి.
సాధన:

(ii) \(\left(\frac{a+i b}{a-i b}\right)^2-\left(\frac{a-i b}{a+i b}\right)^2\) ను x + iy రూపంలో వ్రాయండి.
సాధన:

(iii) \(\frac{(1+i) x-2 i}{3+i}+\frac{(2-3 i) y+i}{3-i}=i\) అయ్యేటట్లు x, y వాస్తవసంఖ్యలు అయితే x, y విలువలను నిర్ధారించండి.
సాధన:

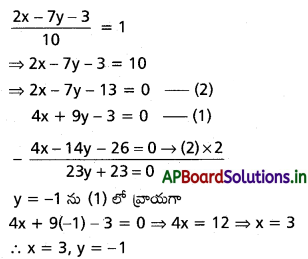
ప్రశ్న 4.
(i) \(\left(\frac{1+i}{1-i}\right)^n=1\) ను తృప్తిపరచే, కనిష్ట ధన పూర్ణాంకం n ను కనుక్కోండి.
సాధన:

∴ n యొక్క కనిష్ట ధన పూర్ణాంకం విలువ 4.
(ii) \(\left(\frac{1+i}{1-i}\right)^3-\left(\frac{1-i}{1+i}\right)^3\) = x + iy అయితే x, y విలువలను కనుక్కోండి.
సాధన:

(iii) \(\frac{3+2 i \sin \theta}{1-2 i \sin \theta}\) ఒక (a) వాస్తవ సంఖ్య (b) శుద్ధ కల్పిత సంఖ్య అయినప్పుడు, θ కు వాస్తవ విలువలను కనుక్కోండి.
సాధన:

![]()
(iv) \(\frac{x-1}{3+i}+\frac{y-1}{3-i}=i\) అయ్యేటట్లు x, y లు వాస్తవ సంఖ్యలు అయితే x, y విలువలను కనుక్కోండి.
సాధన:
\(\frac{x-1}{3+i}+\frac{y-1}{3-i}=i\)
⇒ \(\frac{(x-1)(3-i)+(y-1)(3+i)}{9-i^2}=i\)
⇒ 3x – xi – 3 + i + 3y – iy – 3 – i = 10i
⇒ (3x + 3y – 6) + i(-x + y) = 0 + 10i
వాస్తవ భాగాలను, సంకీర్ణ భాగాలను పోల్చిన
3x + 3y – 6 = 0
⇒ x + y – 2 = 0 …….(1)
-x + y = 10
⇒ x – y + 10 = 0 …….(2)
(1) + (2) ⇒ 2x + 8 = 0
⇒ x = -4
(1) నుండి -4 + y – 2 = 0
⇒ y = 6
∴ x = -4, y = 6