AP Inter 2nd Year Maths 2A Solutions Chapter 4 సమీకరణ వాదం Ex 4(b)

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 4 సమీకరణ వాదం Exercise 4(b) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2A Solutions Chapter 4 సమీకరణ వాదం Exercise 4(b)

అభ్యాసం – 4(బి)

I.

ప్రశ్న 1.
x³ – 3x² – 16x + 48 = 0 సమీకరణం రెండు మూలాల మొత్తం సున్నా అయితే, సమీకరణాన్ని సాధించండి.
సాధన:
x³ – 3x² – 16x + 48 = 0 కు మూలాలు α, β, γ లు
α + β + γ = 3
α + β = 0 (∵ రెండు మూలాల మొత్తం సున్న)
∴ γ = 3
i.e., x – 3 అనేది
x³ – 3x² – 16x + 48 కు కారణాంకం

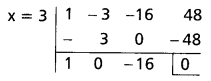
x² – 16 = 0
⇒ x² = 16
⇒ x = ±4
∴ మూలాలు -4, 4, 3

ప్రశ్న 2.
x³ – px² + qx – r = 0 సమీకరణం యొక్క రెండు మూలాల మొత్తం సున్న కావటానికి నియమాన్ని కనుక్కోండి.
సాధన:
మూలాలు α, β, γ లు అనుకుందాం
అప్పుడు α + β + γ = p …….(1)
αβ + βγ + γα = q ……(2)
αβγ = r …….(3)
రెండు మూలాల మొత్తం సున్న కనుక α + β = 0 అనుకోండి.
(1) నుండి γ = p
‘γ’ దత్త సమీకరణానికి మూలం కనుక
γ³ – pγ² + qγ – r = 0
⇒ p³ – p(p²) + q(p) – r = 0
⇒ r = pq
∴ కావలసిన నియమం r = pq

ప్రశ్న 3.
x³ + 3px² + 3qx + r = 0 సమీకరణపు మూలాలు
(i) అంకశ్రేఢిలో వుంటే 2p³ – 3pq + r = 0
(ii) గుణశ్రేఢిలో వుంటే p³r = q³
(iii) హరాత్మక శ్రేఢిలో వుంటే 2q³ = r(3pq – r) అని చూపండి.
సాధన:
దత్త సమీకరణం x³ + 3px² + 3qx + r = 0
(i) మూలాలు అంకశ్రేఢిలో వున్నవి కనుక అవి
a – d, a, a + d అనుకుందాం. అప్పుడు
(a – d) + a + (a + d) = -3p
⇒ 3a = -3p
⇒ a = -p
‘a’ దత్త సమీకరణానికి మూలం, కనుక
a³ + 3pa² + 3qa + r = 0
⇒ (-p)³ + 3p(-p)² + 3q(-p) + r = 0
⇒ -p³ + 3p³ – 3pq + r = 0
⇒ 2p³ – 3pq + r = 0
∴ కావలసిన నియమం 2p³ – 3pq + r = 0

(ii) మూలాలు గుణశ్రేఢిలో వున్నవి కనుక అవి \(\frac{a}{R}\), a, aR అనుకుందాం.
అపుడు మూలాల లబ్ధం = (\(\frac{a}{R}\)) (a) (aR) = -r
⇒ a³ = -r
⇒ a = \((-r)^{1 / 3}\)
‘a’ దత్త సమీకరణానికి మూలం కనుక
a³ + 3pa² + 3qa + r = 0

∴ కావలసిన నియమం p³r = q³

(iii) దత్త సమీకరణం x³ + 3px² + 3qx + r = 0 …….(1)
x = \(\frac{1}{y}\) వ్రాయగా
\(\left(\frac{1}{y}\right)^3+3 p\left(\frac{1}{y}\right)^2+3 q\left(\frac{1}{y}\right)+r=0\)
⇒ 1 + 3py + 3qy² + ry³ = 0
⇒ ry³ + 3qy² + 3py + 1 = 0 ………(2)
(1) యొక్క మూలాలు హరాత్మక శ్రేఢిలో వుంటే, (2) యొక్క మూలాలు అంకశ్రేఢిలో వుంటాయి.
కనుక అవి a – d, a, a + d అనుకుందాం.
(a – d) + a + (a + d) = \(\frac{-3q}{r}\)
⇒ 3a = \(\frac{-3q}{r}\)
⇒ a = \(\frac{-q}{r}\)
‘a’ అనేది (2) కు ఒక మూలం కనుక
ra³ + 3qa² + 3pa + 1 = 0
⇒ \(r\left(\frac{-q}{r}\right)^3+3 q\left(\frac{-q}{r}\right)^2+3 p\left(\frac{-q}{r}\right)+1=0\)
⇒ \(\frac{-q^3}{r^2}+\frac{3 q^3}{r^2}+\frac{3 p q}{r}+1=0\)
⇒ -q³ + 3q³ – 3pqr + r² = 0
⇒ r² – 3pqr + 2q³ = 0
⇒ 2q³ = r(3pq – r)
∴ కావలసిన నియమం 2q³ = r(3pq – r)

ప్రశ్న 4.
x³ – px² + qx – r = 0 సమీకరణ మూలాలు గుణ శ్రేఢిలో ఉండటానికి నియమాన్ని రాబట్టుము.
సాధన:
మూలాలు గుణశ్రేఢిలో వున్నవి. కనుక అవి \(\frac{a}{R}\), a, aR అనుకోండి.
అపుడు మూలాల లబ్దం = (\(\frac{a}{R}\)) (a) (aR) = r
⇒ a³ = r
⇒ a = \(r^{1 / 3}\)
‘a’ దత్త సమీకరణానికి ఒక మూలం కనుక
a³ – pa² + qa – r = 0

∴ కావలసిన నియమం p³r = q³

II.

ప్రశ్న 1.
9x³ – 15x² + 7x – 1 = 0 సమీకరణపు రెండు మూలాలు సమానమైతే, సమీకరణాన్ని సాధించండి.
సాధన:

ప్రశ్న 2.
2x³ + 3x² – 8x + 3 = 0 సమీకరణపు ఒక మూలం, మరోదానికి రెట్టింపు అయిన, ఆ సమీకరణాన్ని సాధించండి.
సాధన:
α, β, γ లు 2x³ + 3x² – 8x + 3 = 0 మూలాలు అనుకుందాం.

ప్రశ్న 3.
x³ – 9x² + 14x + 24 = 0 సమీకరణపు రెండు మూలాలు 3 : 2 నిష్పత్తిలో ఉంటే, ఆ సమీకరణాన్ని సాధించండి.
సాధన:
మూలాలు α, β, γ లు అనుకుందాం.
α + β + γ = 9 …….(1)
αβ + βγ + γα = 14 ……..(2)
αβγ = -24 ………(3)
α : β = 3 : 2 అనుకుందాం.
2α = 3β
⇒ β = \(\frac{2}{3}\)α
(1) నుండి α + \(\frac{2}{3}\)α + γ = 9
γ = 9 – \(\frac{5 \alpha}{3}\) …….(4)
(2) నుండి (α) (\(\frac{2}{3}\)α) + γ(α + β) = 14
⇒ \(\frac{2}{3} \alpha^2+\left(9-\frac{5 \alpha}{3}\right)\left(\alpha+\frac{2}{3} \alpha\right)=14\)
⇒ \(\frac{2}{3} \alpha^2+\left(9-\frac{5}{3} \alpha\right)\left(\frac{5}{3} \alpha\right)=14\)
⇒ 6α² + (27 – 5α) (5α) = 126
⇒ 6α² + 135α – 25α² – 126 = 0
⇒ 19α² – 135α + 126 = 0
⇒ 19α² – 114α – 21α + 126 = 0
⇒ 19α(α – 6) – 21(α – 6) = 0
⇒ (α – 6) (19α – 21) = 0
⇒ α = 6 (లేదా) α = \(\frac{21}{19}\)
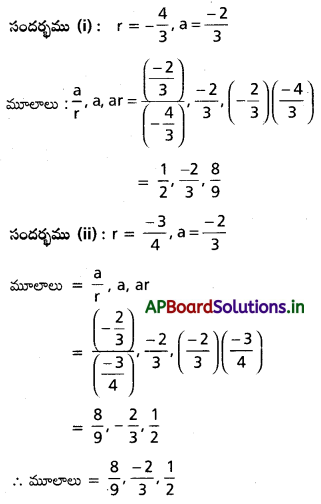
సందర్భము (i): α = 6
β = \(\frac{2}{3}\)α
= \(\frac{2}{3}\) × 6 = 4
γ = 9 – \(\frac{5 \alpha}{3}\)
γ = 9 – \(\frac{2}{3}\) × 6
= 9 – 10
= -1
α = 6, β = 4, γ = -1
αβγ = -24

కానీ αβγ ≠ -24
∴ మూలాలు = 6, 4, -1

ప్రశ్న 4.
మూలాలు అంకశ్రేఢిలో ఉన్న క్రింది సమీకరణాలను సాధించండి.
(i) 8x³ – 36x² – 18x + 81 = 0
సాధన:
మూలాలు అంకశ్రేఢిలో వున్నవి కనుక అవి a – d, a, a + d అనుకొనుము.

(ii) x³ – 3x² – 6x + 8 = 0
సాధన:
మూలాలు అంకశ్రేఢిలో ఉన్నవి కనుక మూలాలు a – d, a, a + d అనుకుందాం.
(a – d) + a + (a + d) = -(-3)= 3
⇒ 3a = 3
⇒ a = 1
(a – d) (a) (a + d) = -8
⇒ a(a² – d²) = -8
⇒ 1(1 – d²) = -8
⇒ d² = 1 + 8 = 9
⇒ d = 3
మూలాలు a – d, a, a + d
= 1 – 3, 1, 1 + 3
= -2, 1, 4

ప్రశ్న 5.
మూలాలు గుణశ్రేఢిలో ఉన్న క్రింది సమీకరణాలను సాధించండి.
(i) 3x³ – 26x² + 52x – 24 = 0
సాధన:
మూలాలు గుణశ్రేఢిలో ఉన్నవి కనుక అవి \(\frac{a}{r}\), a, ar అనుకుందాం.

(ii) 54x³ – 39x² – 26x + 16 = 0
సాధన:
మూలాలు గుణశ్రేఢిలో వున్నవి కనుక అవి \(\frac{a}{r}\), a, ar అనుకుందాం.

ప్రశ్న 6.
మూలాలు హరాత్మకశ్రేఢిలో ఉన్న క్రింది సమీకరణాలను సాధించండి.
(i) 6x³ – 11x² + 6x – 1 = 0
సాధన:
దత్త సమీకరణం 6x³ – 11x² + 6x – 1 = 0 ………(1)
y = \(\frac{1}{x}\) వ్రాయగా
\(6\left(\frac{1}{y}\right)^3-11\left(\frac{1}{y}\right)^2+6\left(\frac{1}{y}\right)-1=0\)
⇒ 6 – 11y + 6y² – y³ = 0
⇒ y³ – 6y² + 11y – 6 = 0 ……(2)
(1) యొక్క మూలాలు హరాత్మక శ్రేఢిలో వుంటే, (2) యొక్క మూలాలు అంకశ్రేఢిలో వుంటాయి.
(2) యొక్క మూలాలు a – d, a, a + d అనుకుంటే,
(a – d) + a + (a + d) = \(-\frac{(-6)}{1}\) = 6
⇒ 3a = 6
⇒ a = 2
మరియు (a – d) (a) (a + d) = \(-\frac{(-6)}{1}\) = 6
⇒ a(a² – d²) = 6
⇒ 2(2² – d²) = 6
⇒ 4 – d² = 3
⇒ d² = 1
⇒ d = 1
(2) మూలాలు a – d, a, a + d
= 2 – 1, 2, 2 + 1
= 1, 2, 3
∴ దత్త సమీకరణానికి మూలాలు = 1, \(\frac{1}{2}\), \(\frac{1}{3}\)

(ii) 15x³ – 23x² + 9x – 1 = 0
సాధన:
దత్త సమీకరణం 15x³ – 23x² + 9x – 1 = 0 …….(1)
x = \(\frac{1}{y}\) వ్రాయగా
\(15\left(\frac{1}{y}\right)^3-23\left(\frac{1}{y}\right)^2+9\left(\frac{1}{y}\right)-1=0\)
⇒ 15 – 23y + 9y² – y³ = 0
⇒ y³ – 9y² + 23y – 15 = 0 ………(2)
(1) యొక్క మూలాలు హరాత్మక శ్రేఢిలో (H.P.) వుంటే, (2) యొక్క మూలాలు అంకశ్రేఢీలో ఉంటాయి.
కనుక ఆ మూలాలు a – d, a, a + d అనుకుందాం.
అప్పుడు (a – d) + (a) + (a + d) = -(-9) = 9
⇒ 3a = 9
⇒ a = 3
మరియు (a – d) (a) (a + d) = -(-15)
⇒ a(a² – d²) = 15
⇒ 3(3² – d²) = 15
⇒ 9 – d² = 5
⇒ d² = 4
⇒ d = 2
∴ (2) యొక్క మూలాలు a – d, a, a + d
= 3 – 2, 3, 3 + 2
= 1, 3, 5
∴ దత్త సమీకరణానికి = 1, \(\frac{1}{3}\), \(\frac{1}{5}\)

ప్రశ్న 7.
పునరావృత మూలాలున్న క్రింది సమీకరణాలను సాధించండి.
(i) x⁴ – 6x³ + 13x² – 24x + 36 = 0
సాధన:
f(x) = x⁴ – 6x³ + 13x² – 24x + 36
f'(x) = 4x³ – 18x² + 26x – 24
ఇప్పుడు f'(3) = 4(3)³ – 18(3)² + 26(3) – 24
= 108 – 162 + 78 – 24
= 0
ఇట్లే f(3) = (3)⁴ – 6(3)³ + 13(3)² – 24(3) + 36
= 81 – 162 + 117 – 72 + 36
= 0
కనుక x – 3; f(x), f'(x) లకు కారణాంకం
∴ f(x) = 0 కు 3 ఆవృత మూలం

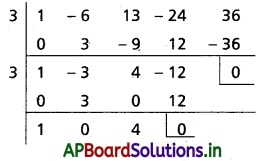
కనుక x² + 4 = 0
⇒ x² = -4
⇒ x = ±2i
∴ దత్త సమీకరణానికి 3, 3, 2i, -2i

(ii) 3x⁴ + 16x³ + 24x² – 16 = 0
సాధన:
f(x) = 3x⁴ + 16x³ + 24x² – 16
f'(x) = 12x³ + 48x² + 48x
= 12x(x² + 4x + 4)
= 12x(x + 2)²
f'(-2) = 0
f(-2) = 3(-2)⁴ + 16(-2)³ + 24(-2)² – 16
= 48 – 128 + 96 – 16
= 0
కనుక f(x), f'(x) లకు (x + 2) కారణాంకం
∴ f(x) = 0 కు -2 ఆవృత మూలం

3x² + 4x – 4 = 0
⇒ 3x² + 6x – 2x – 4 = 0
⇒ 3x(x + 2) – 2(x + 2) = 0
⇒ (x + 2) (3x – 2) = 0
⇒ x = -2, x = \(\frac{2}{3}\)
∴ దత్త సమీకరణానికి -2, -2, -2, \(\frac{2}{3}\)

III.

ప్రశ్న 1.
x⁴+ x³ – 16x² – 4x + 48 = 0 సమీకరణపు రెండు మూలాల లబ్ధం 6 అయితే ఆ సమీకరణాన్ని సాధించండి.
సాధన:
మూలాలు α, β, γ, δ లు అనుకుందాం.
α + β + γ + δ = -1 …….(1)
αβ + αδ + αγ + βγ + βδ + γδ = -16 …….(2)
αβγ + αβδ + βγδ + αγδ = -(-4) = 4 ……….(3)
αβγδ = 48 …….(4)
∵ రెండు మూలాల లబ్దం = 6 కనుక
αβ = 6 అనుకుందాం.
(4) నుండి 6γδ = 48 ⇒ γδ = 8
(3) నుండి 6γ + 6δ + 8β + 8α = 4
⇒ 6(γ + δ) + 8(α + β) = 4
6(γ + δ) + 6(α + β) = -6 – (1) × 6
2(α + β) = 10
α + β = 5
(1) నుండి γ + δ = -1 – 5 = -6
α + β = 5, αβ = 6
(α – β)² = (α + β)² – 4αβ
= (5)² – 4(6)
= 1
α – β = 1
α + β = 5
2α = 6
⇒ α = 3, β = 2
ఇదే విధంగా γ + δ = -6, γδ = 8
(γ – δ)² = (γ + δ)² – 4γδ
= (-6)² – 4(8)
= 36 – 32
= 4
γ – δ = 2
γ + δ = -6
2γ = -4
⇒ γ = -2, δ = -4
∴ దత్త సమీకరణానికి = 3, 2, -2, -4

ప్రశ్న 2.
8x⁴ – 2x³ – 27x² + 6x + 9 = 0 సమీకరణ రెండు మూలాలు ఒకే పరమమూల్యాన్నీ, వ్యతిరేక గుర్తులను కలిగి వుంటే, సమీకరణాన్ని సాధించండి.
సాధన:

ప్రశ్న 3.
18x³ + 81x² + 121x + 60 = 0 సమీకరణపు ఒక మూలం తక్కిన రెండు మూలాల మొత్తంలో సగమైతే, సమీకరణాన్ని సాధించండి. [May ’11, Mar. ’05]
సాధన:

ప్రశ్న 4.
ax⁴ + 4bx³ + 6cx² + 4dx + c = 0 సమీకరణపు మూలాల్లో రెండు జతలు సమానంగా ఉండటానికి నియమాలను రాబట్టండి.
సాధన:
దత్త సమీకరణం ax⁴ + 4bx³ + 6cx² + 4dx + e = 0
⇒ \(x^4+4 \frac{b}{a} x^3+6 \frac{c}{a} x^2+4 \frac{d}{a} x+\frac{e}{a}=0\)
మూలాలు α, α, β, β లు అనుకుందాం
అపుడు మూలాల మొత్తం 2(α + β) = -4\(\frac{b}{a}\)
⇒ α + β = -2\(\frac{b}{a}\)
αβ = k అనుకుంటే α, β లు మూలాలుగా గల వర్గ సమీకరణం
x² – (α + β)x + αβ = 0

⇒ ad² = eb² ఇది మరొక నియమము
∴ కావలసిన నియమాలు 3abc = 2b³ + a²d, ad² = eb²

ప్రశ్న 5.
(i) x⁵ – 5x³ + 5x² – 1 = 0 సమీకరణానికి 3 సమాన మూలాలు ఉంటాయని చూపండి. ఆ మూలాన్ని కనుక్కోండి.
సాధన:
f(x) = x⁵ – 5x³ + 5x² – 1
f'(x) = 5x⁴ – 15x² + 10x = 5x(x³ – 3x + 2)
f'(1) = 5(1) (1 – 3 + 2) = 0
f(1) = 1 – 5 + 5 – 1 = 0
కనుక f(x), f'(x) లకు (x – 1) కారణాంకం
⇒ f(x) = 0 కు 1 ఆవృత మూలం

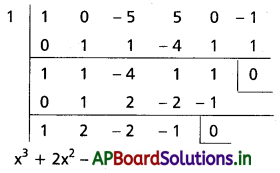
∴ x³ + 2x² – 2x – 1 = 0
x = 1 పై సమీకరణాన్ని తృప్తిపరుస్తుంది.
కనుక f(x) = 0 కు 1 అనేది 3 సార్లు ఆవృత మూలము అవుతుంది.

(ii) x⁵ – 3x⁴ – 5x³ + 27x² – 32x + 12 = 0 సమీకరణం యొక్క పునరావృత మూలాలను కనుక్కోండి
సాధన:
f(x) = x⁵ – 3x⁴ – 5x³ + 27x² – 32x + 12 అనుకోండి.
f'(x) = 5x⁴ – 12x³ – 15x² + 54x – 32
f'(2) = 5(2)⁴ – 12(2)³ – 15(2)² + 54(2) – 32
= 80 – 96 – 60 + 108 – 32
= 188 – 188
= 0
f(2) = 25 – 3(2⁴) – 5(2³) + 27(2²) – 32(2) + 12
= 32 – 48 – 40 + 108 – 64 + 12
= 152 – 152
= 0
కనుక f(x), f'(x) లకు x – 2 కారణాంకం
∴ f(x) = 0 కు 2 ఆవృత మూలం

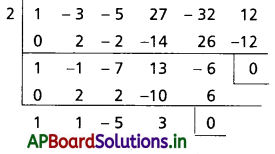
g(x) = x³ + x² – 5x + 3 అనుకుందాం
g'(x) = 3x² + 2x – 5
g'(1) = 3(1)² + 2 – 5 = 0
g(1) = 1 + 1 – 5 + 3 = 0
కనుక g(x), g'(x) లకు x – 1 కారణాంకం
∴ g(x) = 0 కు 1 ఆవృత మూలం

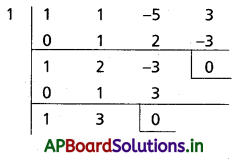
x + 3 = 0 ⇒ x = -3
∴ మూలాలు = 1, 1, 2, 2, -3

ప్రశ్న 6.
8x³ – 20x² + 6x + 9 = 0 సమీకరణం యొక్క పునరావృత మూలాలు కనుక్కోండి.
సాధన:
f(x) = 8x³ – 20x² + 6x + 9 అనుకోండి
f'(x) = 24x² – 40x + 6
= 2(12x² – 20x + 3)
= 2[12x² – 18x – 2x + 3]
= 2[6x(2x – 3) – 1(2x – 3)]
= 2(2x – 3) (6x – 1)
f'(x) = 0
⇒ x = \(\frac{3}{2}\), x = \(\frac{1}{6}\)
\(f\left(\frac{3}{2}\right)=8\left(\frac{3}{2}\right)^3-20\left(\frac{3}{2}\right)^2+6\left(\frac{3}{2}\right)+9\)
= 27 – 45 + 9 + 9
= 0
కనుక x – \(\frac{3}{2}\), f(x), f'(x) లకు కారణాంకం
∴ f(x) = 0 కు \(\frac{3}{2}\) పునరావృత మూలం

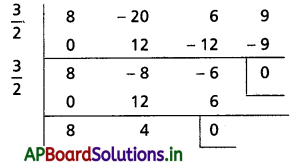
8x + 4 = 0 ⇒ x = \(-\frac{4}{8}=-\frac{1}{2}\)
∴ f(x) = 0 యొక్క మూలాలు \(\frac{3}{2}, \frac{3}{2},-\frac{1}{2}\)