Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 5 ప్రస్తారాలు-సంయోగాలు Exercise 5(b) will help students to clear their doubts quickly.
AP Inter 2nd Year Maths 2A Solutions Chapter 5 ప్రస్తారాలు-సంయోగాలు Exercise 5(b)
అభ్యాసం – 5(బి)
I.
ప్రశ్న 1.
పునరావృతాన్ని అనుమతించినపుడు 1, 2, 4, 5, 7, 8 అంకెలనుపయోగించి ఎన్ని 4 అంకెల సంఖ్యలు ఏర్పరచవచ్చు?
సాధన:
పునరావృతాన్ని అనుమతించినపుడు 1, 2, 4, 5, 7, 8 అంకెలను ఉపయోగించి ఏర్పడే 4 అంకెల సంఖ్యల సంఖ్య = 6 × 6 × 6 × 6
= 64
= 1,296
ప్రశ్న 2.
ప్రతి అక్షరాన్ని ఎన్నిసార్లైనా వాడుకొనే పద్ధతిలో RHYME పదంలోని అక్షరాలతో 5 అక్షరాల పదాలు ఎన్ని ఏర్పరచవచ్చు?
సాధన:
RHYME పదంలో 5 అక్షరాలున్నవి.
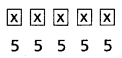
5 అక్షరాలలో పునరావృతాన్ని అనుమతించినపుడు ఏర్పడే 5 అక్షరాల పదాల సంఖ్య = 5 × 5 × 5 × 5 × 5
= 55
= 3,125
ప్రశ్న 3.
5 మూలకాలున్న సమితి A నుంచి 4 మూలకాలున్న సమితి B కి నిర్వచించగల ప్రమేయాలెన్ని?
సాధన:
A లో వున్న మూలకాల సంఖ్య n(A) = 5
B లో వున్న మూలకాల సంఖ్య n (B) = 4
A నుండి B కు గల ప్రమేయాల సంఖ్య = (n(B))n(A)
= 45
= 1024
II.
ప్రశ్న 1.
(i) 0, 2, 4, 6, 8 (iii) 1, 3, 5, 7, 9 అంకెలతో ఏర్పడే 6 అంకెల అనులోమ విలోమాల సంఖ్య ఎంత?
సాధన:
అనులోమ విలోమాల సంఖ్య అనగా మొదటి అంకె, ఆరవ అంకె మరియు రెండవ అంకె, అయిదవ అంకె మరియు మూడవ అంకె, నాలుగవ అంకి ఒకే అంకెలు కలిగి ఉండాలి.
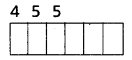
(i) ఇచ్చిన అంకెలు 0, 2, 4, 6, 8
6 అంకెల అనులోమ విలోమాల సంఖ్య కొరకు మొదట స్థానాన్ని నింపగల విధానాల సంఖ్య 4 (సున్న కాకుండా) రెండవ స్థానాన్ని నింపగల విధానాల సంఖ్య 5 మరియు మూడవ స్థానాన్ని నింపగల విధానాల సంఖ్య 5.
0, 2, 4, 6, 8 అంకెలతో ఏర్పడే 6 అంకెల అనులోమా, విలోమాల సంఖ్య = 4 × 52 = 100
(ii) ఇచ్చిన అంకెలు 1, 3, 5, 7, 9
6 అంకెల అనులోమ విలోమాల సంఖ్య కొరకు మొదటి స్థానాన్ని నింపగల విధానాల సంఖ్య 5.
రెండువ మరియు మూడవ స్థానాలను కూడా నింపగల విధానాల సంఖ్య 5.
∴ 1, 3, 5, 7, 9 అంకెలతో ఏర్పడే 6 అంకెల అనులోమ విలోమాల సంఖ్యలు 53 = 125
ప్రశ్న 2.
1, 2, 3, 4, 5, 6 అంకెలనుపయోగించి, కనీసం ఒక అంకె అయినా పునరావృతం అయ్యేలా ఎన్ని 4 అంకెల టెలిఫోన్ నెంబర్లు ఏర్పరచవచ్చు?
సాధన:
6 అంకెలనుపయోగించి పునరావృతాన్ని అనుమతించినపుడు ఏర్పడే 4 అంకెల సంఖ్యలు = 64
పునరావృతం లేనపుడు ఏర్పడే 4 అంకెల సంఖ్యలు 6P4
కనీసం ఒక అంకె అయినా పునరావృతం అయ్యేలా ఏర్పడే 4 అంకెలున్న టెలిఫోన్ నెంబర్లు = 64 – 6P4
= 1296 – 360
= 936
ప్రశ్న 3.
7 మూలకాలున్న సమితి A నుంచి అదే సమితికి ఎన్ని ద్విగుణ ప్రమేయాలు నిర్వచించవచ్చు.
సాధన:
A లోని మూలకాల సంఖ్య n(A) = 7
A నుంచి A కి ద్విగుణ ప్రమేయాల సంఖ్య = n(A)!
= 7!
= 5040
ప్రశ్న 4.
ఇచ్చిన ‘n’ అసరూప వస్తువుల నుంచి ‘r’ వస్తువులతో ఏర్పరచగల ప్రస్తారాలలో ఎన్నింటిలో కనీసం ఒక వస్తువు పునరావృతం అవుతుంది?
సాధన:
‘n’ అసరూప వస్తువుల నుంచి ‘r’ వస్తువులతో ఏర్పరచగల ప్రస్తారాల సంఖ్య.
(i) పునరావృతాన్ని అనుమతించినప్పుడు = nr
(ii) పునరావృతం అనుమతించనప్పుడు = nPr
∴ కనీసం ఒక వస్తువు పునరావృతం అయ్యే ప్రస్తారాల సంఖ్య = nr – nPr
ప్రశ్న 5.
పునరావృతాన్ని అనుమతించినపుడు NATURE పదంలోని అక్షరాలనుపయోగించి ఏర్పరిచే 5 అక్షరాల పదాలలో ఎన్ని పదాలు N తో మొదలవుతాయి?
సాధన:
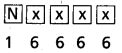
మొదటి స్థానాన్ని N తో నింపాలి. ఈ పనిని ఒకే ఒకవిధంగా చేయవచ్చును.
ఆ తరువాత మిగిలిన నాలుగు స్థానాలను పునరావృతాన్ని అనుమతిస్తున్నాం.
కనుక 6 × 6 × 6 × 6 విధాలుగా నింపవచ్చును = 64
∴ N తో మొదలయ్యే 5 అక్షరాల పదాల సంఖ్య = 1 × 64 = 1296
ప్రశ్న 6.
పునరావృతాన్ని అనుమతించినప్పుడు 0, 1, 2, 3, 4, 5 అంకెలతో ఏర్పరచగల 5 అంకెల సంఖ్యలలో 5తో భాగింపబడిన ఎన్ని?
సాధన:
ఒక సంఖ్య 5తో భాగించబడాలంటే చివరి (ఒకట్ల) స్థానంలో 0 లేదా 5 ఉండాలి. అంటే ఆ స్థానాన్ని 2 విధాలుగా నింపవచ్చు.
ఇక మొదటిస్థానంలో సున్నా ఉండకూడదు. కనుక ఆ స్థానాన్ని 1, లేదా 2, లేదా 3, లేదా 4, లేదా 5తో నింపాలి. ఈ పనిని 5 విధాలుగా చేయవచ్చు.
ఇక మిగిలిన స్థానాలను 6 × 6 × 6 విధాలుగా నింపవచ్చు.
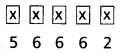
కనుక పునరావృతాన్ని అనుమతించినప్పుడు 0, 1, 2, 3, 4, 5, అంకెలలో ఏర్పరచగల 5 అంకెలున్న సంఖ్యలలో 5తో భాగింపబడే సంఖ్యలు = 5 × 6 × 6 × 6 × 2 = 2160
ప్రశ్న 7.
పునరావృతాన్ని అనుమతించినప్పుడు 1, 2, 3, 4 అంకెలను ఉపయోగించి 2000 కన్నా తక్కువగా ఉన్న 4 అంకెల సంఖ్య లెన్ని ఎర్పరచవచ్చు?
సాధన:
అన్ని ఒక అంకె ఉన్న సంఖ్యలు, రెండు అంకెలున్న సంఖ్యలు, మూడు అంకెలున్న సంఖ్యలు మరియు ఒకటితో మొదలైన నాలుగు అంకెలున్న సంఖ్యలు 2000 కన్నా తక్కువగా ఉన్న 4 అంకెల సంఖ్యలు ఏర్పడతాయి.
ఇచ్చిన అంకెలు {1, 2, 3, 4}
ఒక అంకె ఉన్న సంఖ్యలు 4
పునరావృతాన్ని అనుమతించినప్పుడు
రెండు అంకెలున్న సంఖ్యలు = 4 × 4 = 16
మూడు అంకెల సంఖ్యలు 4 × 4 × 4 = 64
ఒకటితో మొదలయ్యే, నాలుగు అంకెల అంకెలున్న సంఖ్యలు
= (1) (4) (4) (4)
= 64
∴ పునరావృతాన్ని అనుమతించినప్పుడు దత్త అంకెలను ఉపయోగించి 2000 కన్న తక్కువగా ఉన్న 4 అంకెల సంఖ్యలు = 4 + 16 + 64 + 64 = 148
III.
ప్రశ్న 1.
ఒక అక్షరమాలలోని 9 విభిన్న అక్షరాలనుపయోగించి 4 అక్షరాల పదాలు ఏర్పరిస్తే వాటిలో ఎన్ని పదాలలో
(i) అక్షరాలు పునరావృతం కాకుండా ఉంటాయి?
(ii) కనీసం ఒక అక్షరం పునరావృతం అవుతుంది.
సాధన:
(i) పునరావృతం కాకుండా 9 విభిన్న అక్షరాల నుండి 4 అక్షరాలతో ఏర్పడే పదాల సంఖ్య = 9P4
= 9 × 8 × 7 × 6
= 3,024
(ii) పునరావృతాన్ని అనుమతిస్తే 9 విభిన్న అక్షరాల నుండి 4 అక్షరాలలో ఏర్పడే పదాల సంఖ్య = 94 = 6561
∴ కనీసం ఒక అక్షరం పునరావృతం అయ్యే విధంగా 9 విభిన్న అక్షరాల నుండి 4 అక్షరాలలో ఏర్పడే పదాల సంఖ్య = 94 – 9P4
= 6561 – 3024
= 3537
ప్రశ్న 2.
పునరావృతాన్ని అనుమతించినప్పుడు 0, 2, 5, 7, 8 అంకెలనుపయోగించి (i) 2 (ii) 4 తో భాగించబడే 4 అంకెల సంఖ్యలు ఎన్ని ఏర్పరచవచ్చు?
సాధన:
(i) మొదటి స్థానాన్ని (వేల స్థానాన్ని) 2 లేదా 5 లేదా 7 లేదా 8తో నింపాలి.
దీనిని 4 విధాలుగా నింపవచ్చు. ఆ తరువాత వందల స్థానాన్ని 5 విధాలుగా, పదుల స్థానాన్ని 5 విదాలుగా నింపవచ్చు.
ఆ తరువాత ఒకట్ల స్థానంలో 0 లేదా 2 లేదా 8 మాత్రమే ఉండాలి. కనుక ఆ స్థానాన్ని 3 విధాలుగా నింపవచ్చు.
కనుక పునరావృతాన్ని అనుమతించినపుడు 4 అంకెలున్న సరిసంఖ్యలు సంఖ్య = 4 × 5 × 5 × 3 = 300
(ii) ఒక సంఖ్య 4తో భాగించబడాలంటే చివరి రెండు స్థానాలలో ఉండే రెండు అంకెల సంఖ్య 4తో భాగించబడాలి.
కనుక ఈ రెండు స్థానాలను 00, 08, 20, 28, 52, 72, 80, 88 చే 8 విధాలుగా నింపవచ్చును.
మొదటి స్థానాన్ని 0 కాకుండా 4 విధులుగా నింపవచ్చు. రెండవ స్థానాన్ని 5 విధులుగా నింపవచ్చును.
∴ 4తో భాగించబడిన 4 అంకెల సంఖ్యలు = 8 × 4 × 5 = 160
ప్రశ్న 3.
0, 1, 2, 3, 4, 5 అంకెలనుపయోగించి, వాడిన అంకెను ఎన్నిసార్లైనా వాడుతూ 6తో భాగింపబడే 4 అంకెల సంఖ్యలను ఎన్నింటిని ఏర్పరచవచ్చు?
సాధన:
ఇచ్చిన అంకెలు 0, 1, 2, 3, 4, 5 
కావలసిన 4 అంకెల సంఖ్య కొరకు మొదట స్థానాన్ని సున్నాకా కుండ మిగిలిన అంకెలతో నింపగల విధానాల సంఖ్య 5. (పునరావృతాన్ని అనుమతించినపుడు)
రెండవ స్థానాన్ని నింపగల విధానాల సంఖ్య 6. ఇదేవిధంగా మూడవ స్థానాన్ని నింపగల విధానాల సంఖ్య 6.
ఈ విధంగా నింపిన తరువాత చివర స్థానాన్ని ఒక్కొక్క అంకెలతో నింపగా 6 వరుస సంఖ్యలు వచ్చును.
ఈ ఆరు వరుస సంఖ్యలలో ఖచ్చితంగా ఒక సంఖ్య 6 చే భాగించబడును.
∴ 0, 1, 2, 3, 4, 5 అంకెలనుపయోగించి, వాడిన అంకెను ఎన్ని సార్లైనా వాడుతూ 6 తో భాగింపబడే 4 అంకెల సంఖ్యలు = 5 × 6 × 6 × 1 = 1800