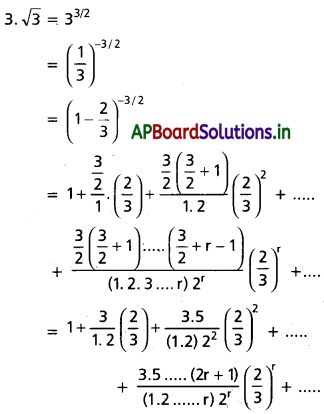Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 6 ద్విపద సిద్ధాంతం Exercise 6(c) will help students to clear their doubts quickly.
AP Inter 2nd Year Maths 2A Solutions Chapter 6 ద్విపద సిద్ధాంతం Exercise 6(c)
అభ్యాసం – 6(సి)
ప్రశ్న 1.
క్రింది సమాసాల విలువలను 4 దశాంశాలకు సవరించి కనుక్కోండి.
(i) \(\sqrt[5]{242}\)
సాధన:

(ii) \(\sqrt[7]{127}\)
సాధన:

(iii) \(\sqrt[5]{32.16}\)
సాధన:

(iv) √199
సాధన:

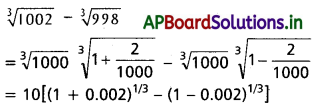
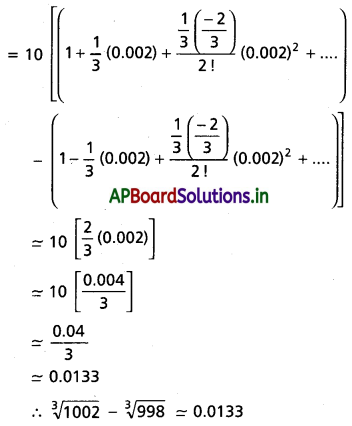
(v) \(\sqrt[3]{1002}-\sqrt[3]{998}\)
సాధన:
(vi) \((1.02)^{3 / 2}-(0.98)^{3 / 2}\)
సాధన:

= 2[0.0299995]
= 0.0599990
≈ 0.059999
∴ \((1.02)^{3 / 2}-(0.98)^{3 / 2}\) = 0.059999
![]()
ప్రశ్న 2.
x2 ఆపై x ఘాతాలు ఉపేక్షించేంతగా |x| స్వల్పమైతే క్రింది సమాసాల ఉజ్జాయింపు విలువలను కనుక్కోండి.
(i) \(\frac{(4+3 x)^{1 / 2}}{(3-2 x)^2}\)
సాధన:

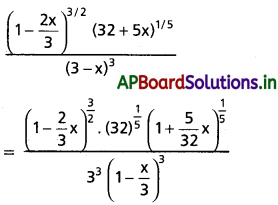
(ii) \(\frac{\left(1-\frac{2 x}{3}\right)^{3 / 2}(32+5 x)^{1 / 5}}{(3-x)^3}\)
సాధన:

(iii) \(\sqrt{4-x}\left(3-\frac{x}{2}\right)^{-1}\)
సాధన:
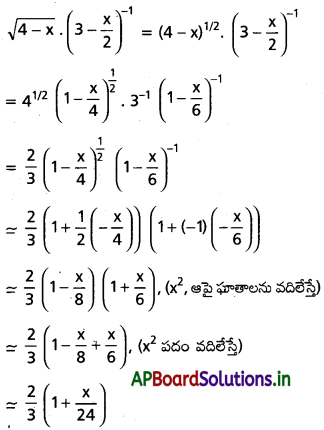
(iv) \(\frac{\sqrt{4+x}+\sqrt[3]{8+x}}{(1+2 x)+(1-2 x)^{-1 / 3}}\)
సాధన:


(v) \(\frac{(8+3 x)^{2 / 3}}{(2+3 x) \sqrt{4-5 x}}\)
సాధన:
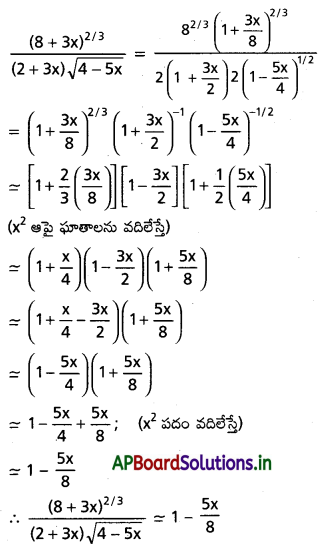
![]()
ప్రశ్న 3.
s, t లు ధన వాస్తవసంఖ్యలు, s తో పోల్చినపుడు t విలువ చాలా తక్కువ అయితే \(\left(\frac{s}{s+t}\right)^{1 / 3}-\left(\frac{s}{s-t}\right)^{1 / 3}\) యొక్క ఉజ్జాయింపు విలువ కనుక్కోండి.
సాధన:
s తో పోల్చినపుడు విలువ చాలా తక్కువ కనుక \(\frac{t}{s}\) అత్యల్పం
∴ |\(\frac{t}{s}\)| < 1

ప్రశ్న 4.
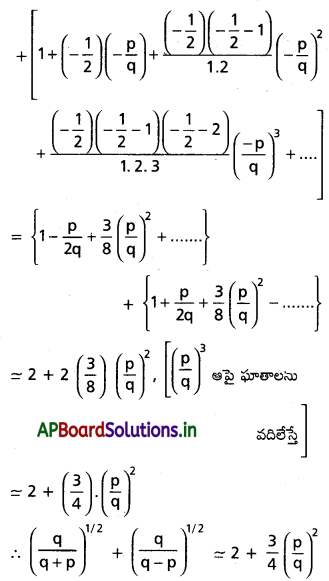
p, q లు ధన వాస్తవ సంఖ్యలు, q తో సరి పోలిస్తే p విలువ చాలా తక్కువ అయితే \(\left(\frac{q}{q+p}\right)^{1 / 2}+\left(\frac{q}{q-p}\right)^{1 / 2}\) యొక్క ఉజ్జాయింపు విలువ కనుక్కోండి.
సాధన:
q తో సరిపోలిస్తే p విలువ చాలా తక్కువ కనుక \(\frac{p}{q}\) అత్యల్పం

ప్రశ్న 5.
x4, ఆపై x ఘాతాలు ఉపేక్షిస్తే \(\sqrt[3]{x^2+64}-\sqrt[3]{x^2+27}\) యొక్క ఉజ్జాయింపు విలువ కనుక్కోండి.
సాధన:

![]()
ప్రశ్న 6.
3√3 విలువను \(\frac{2}{3}\) యొక్క ఆరోహణ ఘాతాలలో వ్రాయండి.
సాధన: