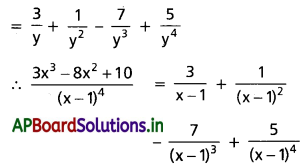AP Inter 2nd Year Maths 2A Solutions Chapter 7 పాక్షిక భిన్నాలు Ex 7(a)

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 7 పాక్షిక భిన్నాలు Exercise 7(a) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2A Solutions Chapter 7 పాక్షిక భిన్నాలు Exercise 7(a)

అభ్యాసం – 7(ఎ)

I. క్రింది భిన్నాలను పాక్షిక భిన్నాలుగా విడగొట్టండి.

ప్రశ్న 1.
\(\frac{2 x+3}{(x+1)(x-3)}\)
సాధన.
\(\frac{2 x+3}{(x+1)(x-3)}=\frac{A}{x+1}+\frac{B}{x-3}\) అనుకుందాం.
∴ 2x + 3 = A(x – 3) + B(x + 1) …..(1)
(1) లో x = -1 వ్రాస్తే, 1 = A(-4) ⇒ A = \(-\frac{1}{4}\)
(1) లో x = 3 వ్రాస్తే, 9 = B(4) ⇒ B = \(\frac{9}{4}\)
\(\frac{2 x+3}{(x+1)(x-3)}=\frac{-1}{4(x+1)}+\frac{9}{4(x-3)}\)

ప్రశ్న 2.
\(\frac{5 x+6}{(2+x)(1-x)}\)
సాధన:
\(\frac{5 x+6}{(2+x)(1-x)}=\frac{A}{2+x}+\frac{B}{1-x}\) అనుకుందాం.
5x + 6 = A(1 – x) + B(2 + x) …..(1)
(1) లో x = -2 వ్రాస్తే, -10 + 6 = A(1 + 2) ⇒ A = \(-\frac{4}{3}\)
(1) లో x = 1 వ్రాస్తే, 5 + 6 = B(2 + 1) ⇒ B = \(\frac{11}{3}\)
∴ \(\frac{5 x+6}{(2+x)(1-x)}=-\frac{4}{3(2+x)}+\frac{11}{3(1-x)}\)

II.

ప్రశ్న 1.
\(\frac{3 x+7}{x^2-3 x+2}\)
సాధన:
\(\frac{3 x+7}{x^2-3 x+2}=\frac{3 x+7}{(x-1)(x-2)}=\frac{A}{x-1}+\frac{B}{x-2}\) అనుకుందాం.
3x + 7 = A(x – 2) + B(x – 1) ……(1)
(1) లో x = 1 వ్రాస్తే, 10 = -A ⇒ A = -10
(1) లో x = 2 వ్రాస్తే, 13 = B
∴ \(\frac{3 x+7}{x^2-3 x+2}=\frac{-10}{x-1}+\frac{13}{x-2}\)

ప్రశ్న 2.
\(\frac{x+4}{\left(x^2-4\right)(x+1)}\) [Mar. ’14]
సాధన:
\(\frac{x+4}{\left(x^2-4\right)(x+1)}=\frac{A}{x+1}+\frac{B}{x+2}+\frac{C}{x-2}\)
x + 4 = A(x2 – 4) + B(x + 1)(x – 2) + C(x + 1)(x + 2) …….(1)
(1) లో x = -1 వ్రాస్తే, 3 = A(1 – 4)
⇒ 3 = -3A
⇒ A = -1
(1) లో x = -2 వ్రాస్తే,
2 = B(-2 + 1) (-2 – 2)
⇒ 2 = 4B
⇒ B = \(\frac{1}{2}\)
(1) లో x = 2 వ్రాస్తే,
6 = C(2 + 1) (2 + 2)
⇒ 6 = 12C
⇒ C = \(\frac{1}{2}\)
∴ \(\frac{x+4}{\left(x^2-4\right)(x+1)}=-\frac{1}{x+1}+\frac{1}{2(x+2)}+\frac{1}{2(x-2)}\)

ప్రశ్న 3.
\(\frac{2 x^2+2 x+1}{x^3+x^2}\)
సాధన:
\(\frac{2 x^2+2 x+1}{x^3+x^2}=\frac{2 x^2+2 x+1}{x^2(x+1)}=\frac{A}{x}+\frac{B}{x^2}+\frac{C}{x+1}\)
2x² + 2x + 1 = Ax(x + 1) + B(x + 1) + Cx² ……(1)
(1) లో x = 0 వ్రాస్తే, 1 = B
(1) లో x = -1 వ్రాస్తే, 2 – 2 + 1 = C(1) ⇒ C = 1
ఇరువైపులా x² గుణకాలు పోల్చగా
2 = A + C
⇒ A = 2 – C
= 2 – 1
= 1
∴ \(\frac{2 x^2+2 x+1}{x^3+x^2}=\frac{1}{x}+\frac{1}{x^2}+\frac{1}{x+1}\)

ప్రశ్న 4.
\(\frac{2 x+3}{(x-1)^3}\)
సాధన:
\(\frac{2 x+3}{(x-1)^3}\)
x – 1 = y అనుకుంటే x = y + 1
⇒ \(\frac{2 x+3}{(x-1)^3}=\frac{2(y+1)+3}{y^3}=\frac{2 y+5}{y^3}\)

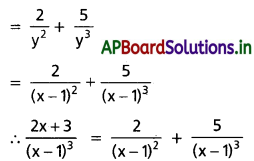
ప్రశ్న 5.
\(\frac{x^2-2 x-6}{(x-2)^3}\)
సాధన:
x – 2 = y అనుకొనుము
⇒ x = y + 2

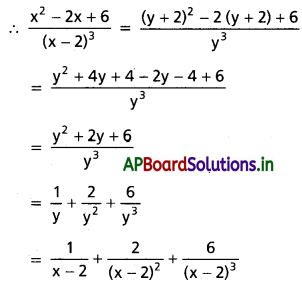
III.

ప్రశ్న 1.
\(\frac{x^2-x+1}{(x+1)(x-1)^2}\)
సాధన:
\(\frac{x^2-x+1}{(x+1)(x-1)^2}=\frac{A}{x+1}+\frac{B}{x-1}+\frac{C}{(x-1)^2}\) అనుకుందాం.
x² – x + 1 = A(x – 1)² + B(x + 1)(x – 1) + C(x + 1) …….(1)
x = -1 వ్రాస్తే, 1 + 1 + 1 = A(4) ⇒ A = \(\frac{3}{4}\)
x = 1 వ్రాస్తే, 1 – 1 + 1 = C(2) ⇒ C = +\(\frac{1}{2}\)
1 లో x² గుణకాలను పోల్చగా
A + B = 1
⇒ B = 1 – A
⇒ B = 1 – \(\frac{3}{4}\)
⇒ B = \(\frac{1}{4}\)
∴ \(\frac{x^2-x+1}{(x+1)(x-1)^2}=\frac{3}{4(x+1)}+\frac{1}{4(x-1)}+\frac{1}{2(x-1)^2}\)

ప్రశ్న 2.
\(\frac{9}{(x-1)(x+2)^2}\)
సాధన:
\(\frac{9}{(x-1)(x+2)^2}=\frac{A}{x-1}+\frac{B}{x+2}+\frac{C}{(x+2)^2}\) అనుకొందాం.
9 = A(x + 2)² + B(x – 1) (x + 2) + C(x – 1) ……(1)
x = 1 వ్రాస్తే, 9 = 9A ⇒ A = 1
x = -2 వ్రాస్తే, 9 = -3C ⇒ C = -3
(1) లో x² గుణకాలను పోల్చగా
A + B = 0
⇒ B = -A = -1
∴ \(\frac{9}{(x-1)(x+2)^2}=\frac{1}{x-1}-\frac{1}{x+2}-\frac{3}{(x+2)^2}\)

ప్రశ్న 3.
\(\frac{1}{(1-2 x)^2(1-3 x)}\)
సాధన:
\(\frac{1}{(1-2 x)^2(1-3 x)}=\frac{A}{1-3 x}+\frac{B}{1-2 x}+\frac{C}{(1-2 x)^2}\) అనుకుందాం.
1 = A(1 – 2x)² + B(1 – 3x) (1 – 2x) + C(1 – 3x) ……..(1)
x = \(\frac{1}{3}\) వ్రాస్తే, 1 = A\(\left(1-\frac{2}{3}\right)^2\)
⇒ 1 = \(\frac{A}{9}\)
⇒ A = 9
x = \(\frac{1}{2}\) వ్రాస్తే, 1 = C(1 – \(\frac{3}{2}\))
⇒ 1 = \(-\frac{C}{2}\)
⇒ C = -2
(1) లో x² గుణకాలను పోల్చగా
0 = 4A + 6B
6B = -4A – 36
B = -6
∴ \(\frac{1}{(1-2 x)^2(1-3 x)}=\frac{9}{1-3 x}-\frac{6}{1-2 x}-\frac{2}{(1-2 x)^2}\)

ప్రశ్న 4.
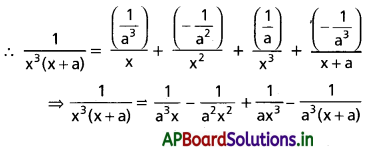
\(\frac{1}{x^3(x+a)}\)
సాధన:
\(\frac{1}{x^3(x+a)}=\frac{A}{x}+\frac{B}{x^2}+\frac{C}{x^3}+\frac{D}{x+a}\) అనుకుందాం.
= \(\frac{A \cdot x^2(x+a)+B(x)(x+a)+C(x+a)+D x^3}{x^3(x+a)}\)
∴ 1 = A(x²) (x + a) + Bx(x + a) + C(x + a) + Dx³ ……..(1)
x = 0 ను (1) లో వ్రాస్తే, 1 = A(0) + B(0) + C(0 + a) + D(0)
⇒ 1 = C (a)
⇒ C = \(\frac{1}{a}\)
x = -a ను (1) లో వ్రాస్తే, 1 = A(0) + B(0) + C(0) + D(-a)³
⇒ 1 = D(-a³)
⇒ D = \(-\frac{1}{a^3}\)
(1) లో x³ గుణకాలను పోల్చగా
0 = A + D
⇒ A = -D
⇒ A = \(\frac{1}{a^3}\)
(1) లో x² గుణకాలను పోల్చగా
0 = Aa + B
⇒ B = -aA
⇒ B = \(-a\left(\frac{1}{a^3}\right)\)
⇒ B = \(-\frac{1}{a^2}\)

ప్రశ్న 5.
\(\frac{x^2+5 x+7}{(x-3)^3}\)
సాధన:

ప్రశ్న 6.
\(\frac{3 x^3-8 x^2+10}{(x-1)^4}\)
సాధన: