AP Inter 2nd Year Maths 2B Important Questions Chapter 4 దీర్ఘవృత్తం

Students get through AP Inter 2nd Year Maths 2B Important Questions Chapter 4 దీర్ఘవృత్తం which are most likely to be asked in the exam.

AP Inter 2nd Year Maths 2B Important Questions Chapter 4 దీర్ఘవృత్తం

ప్రశ్న 1.
క్రింది దీర్ఘవృత్తాలకు ఉత్కేంద్రత, నాభుల నిరూపకాలు, నాభి లంబం పాడవు, నియత రేఖల సమీకరణాలు కనుక్కోండి.
(i) 9 x²+16 y²-36 x+32 y-92=0
సాధన:
దీర్ఘవృత్తం సమీకరణం
9 x²+16 y²-36 x+32 y-92=0
9(x²-4 x+4)+16(y²+2 y+1)
=92+36+16

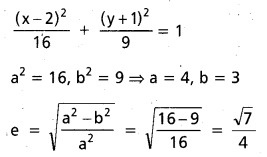
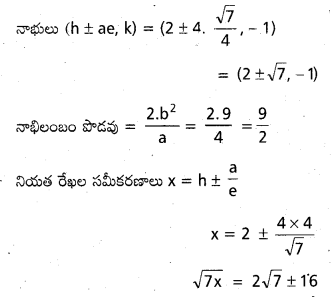
(ii) 3 x²+y²-6 x-2 y-5=0
సాధన:
3(x²-2x)+(y²-2 y)=5
3(x²-2 x+1)+(y²-2 y+1)=9
3(x-1)²+(y-1)²=9

ప్రశ్న 2.
X, Y అక్షాలు వరుసగా దీర్ఘ్కం 1 హ్రస్వాక్షంగా కలిగి, నాభి లంబం పొడవు 4, నాఘుల మధ్య దూరం \(4 \sqrt{2}\) గా గల దీర్ఘవృత్త సమీకరణం కనుక్కోండి.
సాధన:

ప్రశ్న 3.
నాభిలంబం పొడవు, హస్వాక్షం పొడవులో సగం ఉండే దీర్ఘవృత్తం (ప్రామాణిక రూపంలో) ఉత్కేంద్రత కనుక్కోండి.
సాధన:

ప్రశ్న 4.
దీర్ఘవృత్తం \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\)=1 నాఖి జ్యా అగ్రాల (శీర్షాలు కాని) (a > b) ఉత్కేంద్రతా కోణాల θ¹, θ²e ల
ఉత్కేంద్రత అయితే
(i) \(e \cos \frac{\left(\theta_1+\theta_2\right)}{2}=\cos \frac{\theta_1-\theta_2}{2}\)
(ii) \(\frac{\mathbf{e}+\mathbf{1}}{\mathbf{e}-1}=\cot \left(\frac{\theta_1}{2}\right) \cot \left(\frac{\theta_2}{2}\right)\) అని చూపండి.
సాధన:

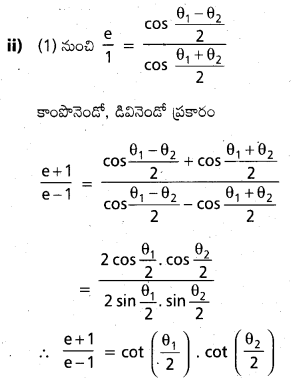
ప్రశ్న 5.
దీర్ఘవృత్తం \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) కేంద్రం C, AA’, BB’ వరుసగా దీర్ఘ, (హస్వాక్షాలు, దీర్ఘవృత్తంపై ఏదైనా బిందువు P యొక్క బిందు y నిరూపకం (PN) అయితే \(\frac{(\mathrm{PN})^2}{(\mathrm{~A} N (\mathrm{AN})}=\frac{(\mathrm{BC})^2}{(\mathrm{CA})^2}\)
సాధన:

ప్రశ్న 6.
ఒక దీర్ఘ వృత్తం నాభులు S, T లు, హ్రస్వాక్కపు ఒక కొన STB ఒక సమబాహం త్రిభుజం అయితే, దీర్ఘవృత్తం ఉత్కేంద్రత కనుక్కోండి.
సాధన:

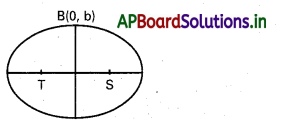
దీర్ఘవృత్తం సమీకరణం \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
(ae, 0), T(-ae, 0) లు నాభులు
B(0, b)(హస్వాక్షం కొన
STB సమబాహు త్రిభుజం
S B=ST ⇒ S B²=S T²
a² e²+b²=4 a² e²
b²=3 a²e²
a²e² =3a²e²
1-e²=3e²
e²=1
e²= \(\frac{1}{4}\)
∴ దీర్ఘవృత్తం ఉత్కేంద్రత = \(\mathrm{e}=\frac{1}{2}\)

ప్రశ్న 7.
దీర్ఘ వృత్తం \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) (a>b) మీది బిందువులలో (-a, 0),(a, 0) బిందువులు, నాభి (a e, 0) నుంచి వరసగా అత్యధిక, అత్యల్ప దూరాలలో ఉంటాయని మూపండి.
సాధన:
P=(x, y) దీర్ఘ్ వృత్తం మీద ఏదైనా బిందువనుకొంటే, -a≤x≤a  అవుతుంది. నాభి S=ae, 0)
(x,y) దీర్ఘవృత్తం మీది బిందువు కాబట్టి
\(y^2=\frac{b^2}{a^2}\left(a^2-x^2\right)\)
= (1-e²) (a²-x²)[∵ b²=a² (1-e²)] ……………… (1)
SP²=(x-ae)²+y²
=(x-ae)²+ (1-e²) (a²-x²)
=-2 xae+a²+e² x²
=[a-ex]²
∴ SP=|a-ex|
-a ≤ x ≤ a
⇒ -ae ≤ xe ≤ ae
⇒ -ae – a ≤ xe – a ≤ ae-a ……………… (2)
∴ ex -a<0
∴ SP=a-ex ……………… (3)
(2) నుంచి (3)
ae +a ≥ SP ≥ a – ae అవుతుంది
⇒ a-ae ≤ S P ≤ ae+a
P=(-a, 0) అయినప్పుడు SP గరిష్ఠ విలువ ae + a
P=(a, 0) అయినప్పుడు SP కరిష్ఠ విలువ a-a e అవుతుంది.
∴ అత్యల్ప దూరంలో ఉండే బిందువు (a, 0)
∴  అత్యధిక దూరంలో ఉండే బిందువు (-a, 0)

ప్రశ్న 8.
వ్యుత్రేంద్రత \(\frac{1}{60}\) కలిగిన దీర్ఘవృత్తాకార కక్ష్మలో భూమి తిరుగుతుంది. ఆ కక్ష్య దరర్ఘాక్షం పొడవు సుమారుగా
186 x 10⁶ మైళ్ల. సూర్యుడు ఆ కక్ష్య యొక్క ఒక నాభి వద్ద ఉన్నప్పుడు, సూర్యుడి నుండి భూమి అత్యల్ప, అత్యధిక దూరాలను కనుక్కోండి.
సాధన:
భూమి కక్ష్య మొక్క సమీకరణం \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\)=1.
(a > b) అనుకొందాం.
దీర్ఘాక్షం పొడవు 186 x 10⁶ మైళ్లు కనుక
2 a =186 x 10⁶ మైళ్ల.
∴ a =93 x 10⁶  మైళ్ల.
కక్ష్య వ్యుక్కేంద్రత e= \(\frac{1}{60}\)
సూర్యుడి నుండి భూమికి గల అత్యల్ప, అత్యధిక దూరాలు వరసగా a+ ae, a – ae అని తెలుసు.
ఇక్కడ, అత్యధిక దూరం =93 \(\times 10^6 \times\left(1+\frac{1}{60}\right)\) మైళ్ల
=9455 x  10⁴ మైళ్ల.
మైళ్లు అత్లల్ప దూరం =93 x 10⁶ x \(\left(1-\frac{1}{60}\right)\)
= 9145 x 10⁴ మైళ్ల.

ప్రశ్న 9.
ఒకటో పాదంలో నాఖి లంబాగ్రం వద్ద 9 x²+16 y² = 144 దీర్ఘవృత్టానికి స్పర్శరేఖ, అభిలంబ రేఖల సమీకరణాలి కనుక్కోండి.
సాధన:
దీర్ఘవృత్తం 9x²+16 y²=144

ప్రశ్న 10.
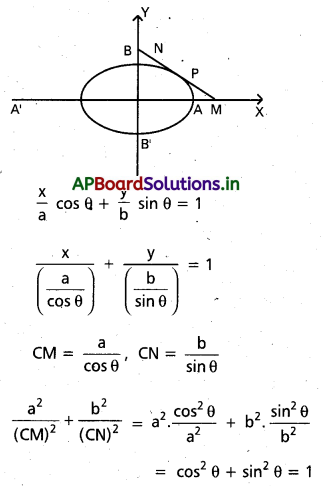
దీర్ఘవృత్తం \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1(a>b) కేంద్రం C. దీర్ఘ వృత్తఫ స్పర్యరేఖ దీర్ఘ ప్రసస్వాక్షాలను వరంసగా M, N ల వద్ద ఖండిస్తే \(\frac{a^2}{(C M)^2}+\frac{b^2}{(C N)^2}\)= 1 అని చూపడి.
సాధన.
P(a cosθ, b sinθ) దీర్ఘవృత్తం మీద ఏదేని ఐిందువు.
P(θ) వద్ద స్పర్శరేఖ సమీకరణము

ప్రశ్న 11.
(i) \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\)=1 దీర్ఘవృత్తానికి 1 x+m y+n=0 స్పర్శరేఖ కావడానికి.
(ii) \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\)=1 దీశ్ఘృత్తాలి 1 x+m y+n=0 అభిలంబ రేఖ కావడానికి నియమాలు కనుక్రోండి. సాధన:
(i) దీర్ఘవృత్తము సమీకరణము \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\)=1.
P(θ) వద్ద స్వర్శరేఖ సమీకరణము
\(\frac{x}{a} \cos \theta+\frac{y}{b} \sin \theta\)=1 ——-(1)
దత్తరేఖ సమీకరణము lx + my =-n ——-(2)
(1), (2) ఒకే రేఖను సూచిస్తున్నాయి.
గుణకాలను పోల్చగా

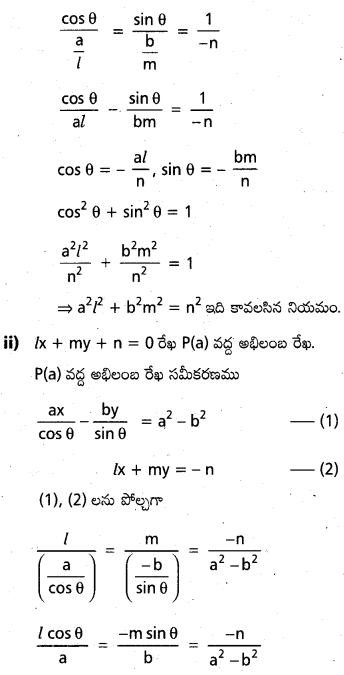
ప్రశ్న  12.
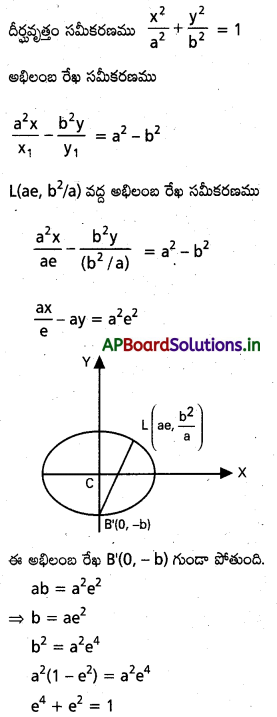
దీర్ఘవృత్తం \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\)=1 నాఖిలంబం ఒక కొన వద్ద అథిలంణ రేఖ హ్రస్వాక్గం ఒక కొన ద్వారా పోతే e⁴+e² = 1 అని చూపండి. [దీర్ఘవృత్తం ఉత్కేంద్రత e]
సాధన:

ప్రశ్న 13.
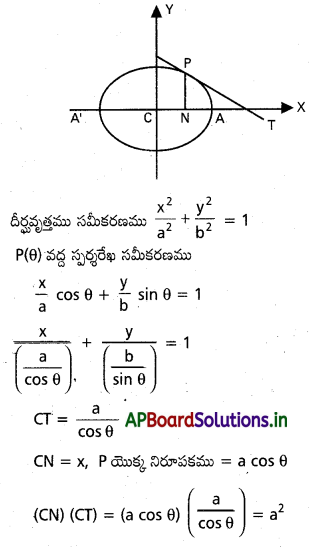
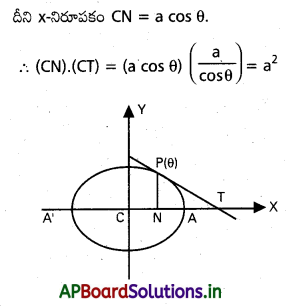
దీర్ఘవృత్తం \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) పై బిందువు P, y- నిరూపకం (P. N), P వద్ద స్పర్శరేఖ – అక్షాస్ని; T = వద్ద ఖండిస్తే (CN) (CT) =a² అని చూపండి. (దీర్ఘ వృత్తం కేంధ్రం C ).
సాధన:

ప్రశ్న 14.
దీర్ఖవృత్తం \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) పై విందువు P, y- నిరాపకం (PN). P వద్ద స్రరశగేీఖ X – అక్షాన్ని T వద్ద ఖండిస్తే (CN) (CT)=a² అని చూఫండి (దీర్ఘ వృత్త కేంద్రం C).
సాధన:

ఒక దీర్ఘ్య వృత్తం లంబ స్పర్శరేఖల ఖండన బిందువులు ఒక వృత్తంపై ఉంటాయని చూపండి.
దీర్ఘ వృత్త సమీకరణం \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 (a > b)\) అనుకొందాం. దీనికి వాలు- అంతరఖండ రూపంలో ఏదైనా స్పర్శరేఖ y=m x \(\pm \sqrt{a^2 m^2+b^2}\)
లంబ స్పర్శరేఖల ఖండన బిందువు P (x₁, y₁) అనుకొందాం. ఏదో ఒక వాస్తవ విలువ m కు P మిందువ పై (1) ఉంటుంది.

[స్పర్శ రేఖలు పరస్పర లంబ రేఖలు కాబట్టి m₁ m₂=-1]
y₁² -b²=-x₁²+a²
x₁²+y₁² =a²+b²
P (x₁, y₁) బిందుపథము x²+y²=a²+b²
అంటే x₁²+y₁²=a²+b²
అంతేగాక, లందస్పర్శరేఖలలో ఒకటి ఉర్థ్వ రేఖ అయితే అవి ( ±a, ±b) లలో ఒక బిందువు వద్ద ఖండించుకొంటాయి.
బిందువులన్నీ x²+y²=a²+b² ని తృప్తి పరుస్తాయి.
∴ S =0 దీర్ఘ వృత్తం లంబస్పర్శరేఖల ఖండన బిందవులు
x²+y² = a²+b² అనే వృత్తం పై ఉంటాయి.

ప్రశ్న 15.
ఒక వృత్తం ఒక దీర్ఘ వృత్తంతో సకేంద్రీయంగా ఉంటే వాటి ఉమ్మడి స్రాశరేఖ దీర్ఘవృత్తం దీర్ఘాక్షంతో చేసే నిమ్నతను కనుక్కోండి.
సాధన:
వృత్తం, దీర్ఘ వృత్తం సమీకరణాలను వరసగా x²+y²= r², \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\),(a>b) అనుకొందాం.
అప్పుడు దీర్ఘవృత్త దీర్ఖాక్షం X-అక్షం అవుతుంది.
r<b<a అయితే వృత్తం హూర్తిగా దీర్ఘ వృత్తం లోపల ఉంటుంది. కాబట్టి, ఉమ్మడి స్పర్యరేఖ ఉండదు.
b <a<r అయితే, దీర్ఘవృత్తం హూర్తిగా వృత్తం లోపల ఉంటుంది.
కాబట్టి, వాటికి ఉమ్మడి స్పర్శరేఖ ఉండదు.
కాబట్టి, b<r<a కావాలి.
సందర్భం (i) : b<r<a
ఏదైనా ఒక ఉమ్మడి స్పర్శరేఖ, X-అక్షం ఝొక్క ధనదిశతో ‘θ’ కోణం చేస్తుందనుకొందాం.

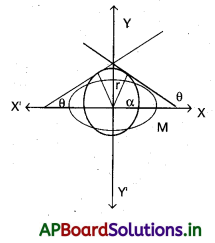
ఉమ్మడి స్పర్శర్ఖే, వృత్తాన్ని స్పృశించే బిందువుగుండా పోమే వ్యాసార్థం X-క్షం యొక్క ధనదిశతో α కోణం చేస్తుందను కొంటే, ఉమ్మడి స్పర్శరేఖా సమీకరణం x cos α+y sin α =r అవుతుంది.

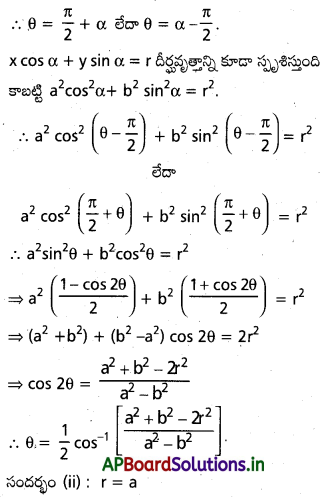
ఈ సందర్భంలోవృత్తం, దీర్ఘ వృత్తం మొక్క దీర్హాక్షపు అంత్య బిందువుల వద్ద, దీర్ఘవృత్తాన్ని స్పృశిస్తుంది. అప్పుడు ఉమ్మడి స్పర్శరేఖలు x=±a అవుతాయి. θ=\(\frac{\pi}{2}\) అవుతుంది. సందర్భం (iii) : r=b
ఈ సందర్భంలో వృత్తం, దీర్ఘవృత్తం యొక్క (హస్వాక్షపు) అంత్యబిందువుల వద్ద దీర్ఘవృత్తాన్ని స్పృశిస్తుంది. అప్పుడు ఉమ్మడి స్రర్శరేఖలు y=± b అవుతాయి. θ=0 అవుతుంది.