AP Inter 2nd Year Maths 2B Important Questions Chapter 6 సమాకలనం

Students get through AP Inter 2nd Year Maths 2B Important Questions Chapter 6 సమాకలనం which are most likely to be asked in the exam.

AP Inter 2nd Year Maths 2B Important Questions Chapter 6 సమాకలనం

ప్రశ్న 1.
R మీద ∫ 2x⁷ dx ను కనుక్కోండి
సాధన:

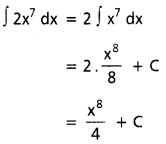
ప్రశ్న 2.
I ⊂ R {nπ: n ∈ Z} మీద ∫ cot ² x dx, ను గణించండి.
సాధన:
∫cot ² x d x ∫ =(cosec² x-1) dx
=cosec² x dx-∫d x
= – cot x – x+C

ప్రశ్న 3.
x∈R \(\int\left(\frac{x^6-1}{1+x^2}\right) d x\) ను గణించండి.
సాధన:

ప్రశ్న 4.
∫(1-x)(4-3 x)(3+2 x) dx, x ∈ R న కనుక్కోండి.
సాధన:

ప్రశ్న 5.
\(\int\left(x+\frac{1}{x}\right)^3\) గణించండి
సాధన:

ప్రశ్న 6.
R మీద \(\int \sqrt{1+\sin 2 x} \) dx విలువ కనుక్కోండి.
సాధన:

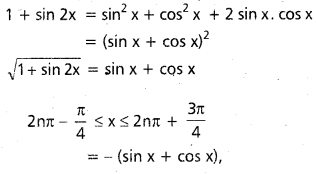
ప్రశ్న 7.
x>0 అయితే \(int \frac{2 x^3-3 x+5}{2 x^2} dx\) ను గణించండి. ఫలితాన్ని అవకిలనం చేసి సరిచూడండి.
సాధన:

ప్రశ్న 8.
R మీద \(\int \frac{x^5}{1+x^{12}} d x\) ను గణించండి.
సాధన:

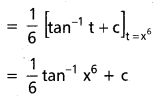
ప్రశ్న 9.
R మీద cos³x  sin xdx ను గణించండి.
సాధన:

ప్రశ్న 10.
I=(0,∞) మీద \(\int\left(1-\frac{1}{x^2}\right) e^{\left(x+\frac{1}{x}\right)} d x\) ను కనుక్కోండి.
సాధన:

ప్రశ్న 11.
I = (0,1) మీద \(\int \frac{1}{\sqrt{\sin ^{-1} x} \sqrt{1-x^2}} d x\) ను గణించండి.
సాధన:

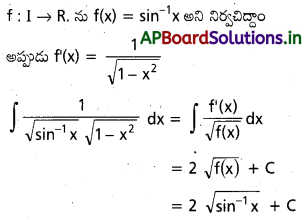
ప్రశ్న 12.
\(\mathbf{x} \in \mathbf{I} \subset \mathbf{R} \backslash\left\{\frac{(\mathbf{2 n}+\mathbf{1}) \pi}{2}: \mathbf{n} \in \mathbf{z}\right\}\) అయితే \(\int \frac{\sin ^4 x}{\cos ^6 x}\)
సాధన:

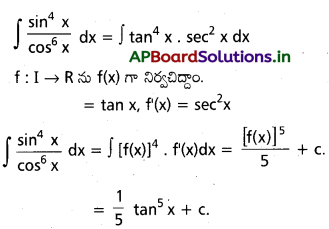
ప్రశ్న 13.
R మీద sin² xdx ను గణించండి.
సాధన:

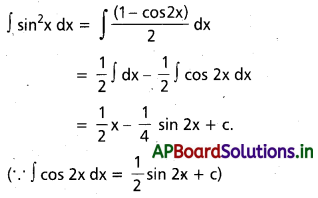
ప్రశ్న 14.
a,b∈R,a²+b² ≠0 అయితే ∫ \(\frac{1}{a \sin x+b \cos x} dx\) ను గణించండి.
సాధన:
a=r cos θ, b=r sin θ అయ్యేటట్లు రండు వాస్తవ సంఖ్యలు r, θ లను కనుక్కోండి

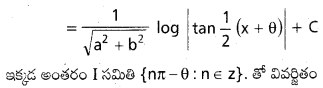
ప్రశ్న 15.
(-5,∞) మీద ∫ \(\frac{x^2}{\sqrt{x+5}} dx\)
సాధన:

ప్రశ్న 16.
∫ \(\frac{x}{\sqrt{1-x}} dx\) x∈I (o,1) విలువ కనుక్కోండి.
సాధన:

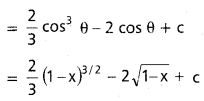
ప్రశ్న 17.
(-4, ∞) మీద  ∫ \(\frac{d x}{(x+5) \sqrt{x+4}}\) ను గణించండి.
సాధన:

ప్రశ్న 18.
\(I=\left(-\frac{2}{3}, \frac{2}{3}\right)\) మీద ∫ \(\frac{d x}{\sqrt{4-9 x^2}}\) విలువ కనుక్కోండి.
సాధన:

ప్రశ్న 19.
x ∈ I = (-a,a)  ∫ \(\frac{1}{a^2-x^2}\) dx ను గణించండి.
సాధన:

ప్రశ్న 20.
R మీద \(\int \frac{1}{1+4 x^2} dx\) ను గణించండి.
సాధన:

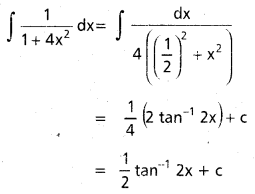
ప్రశ్న 21.
(-2,2) మీద ∫ \(\frac{1}{\sqrt{4-x^2}} dx\) ను గణించండి.
సాధన:

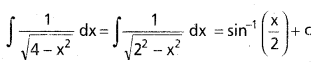
ప్రశ్న 22.
R మీద \(\sqrt{4 x^2+9} dx \) ను గణించండి.
సాధన:

ప్రశ్న 23.
\(\left[\frac{5}{3}, \infty\right) \text { మీద } \int \sqrt{9 x^2-25} \mathrm{dx}\) ను గణించండి.
సాధన:

ప్రశ్న 24.
\(\frac{-4}{5}, \frac{4}{5}\) మీద ∫ \(\sqrt{16-25 x^2}\) dx ను గణించండి.
సాధన:

ప్రశ్న 25.
(-1,1) మీద ∫ x sin^-1 x dx ను గణించండి.
సాధన:

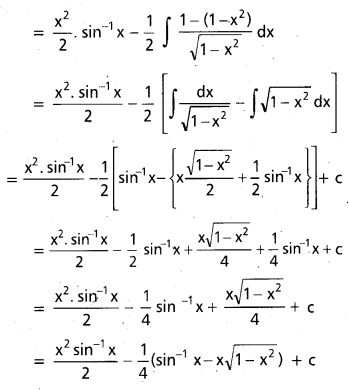
ప్రశ్న 26.
∫ x² cosx dx ను గణణించండ.
సాధన:
u(x)=x², v(x)=\sin x అనుకొండి.
v’(x)=cos x
u(x) v’(x)=x² cos x
విభాగ సమాకలన సూరతం నుంచ
∫ x².cos x d x=x² sin x-∫ sin x(x²)’ d x
= x² sin x-2 ∫ x sin x d x+c₁
ఇంకోసారి విభాగ సమాకలన సూత్రాన్ని
∫ x sin x dx, కు అనువర్తనం చేస్తే
∫ x. sin x dx =  – x cos x  – ∫ (-cos x) dx
= – x cos x + sin x+ c₂
x²cos  = x² sinx – 2(sinx – x cosx)+c
= x² sin x -2 sin x+2x cos x+c
= (x²– 2) sinx+ 2x cos x+c
విభాగ సమాకలన సూత్రాన్ని ఉపయోగించి, కొన్ని సమాకల నులను గణించేటప్పుడు, రెండు లేదా మూడుసార్లు సూత్రాన్ని ఉపయోగించిన తరువాత దత్తసమాకలనగుర్తు తేడాతో రావచ్చు, ఇచ్చిన సమాకలనాన్ని గణించడానికి ఇదిఎంతగానో ఉపసంఖ్య.

ప్రశ్న 27.
R మీద ∫ e^x sin x dx ను గణించండి.
సాధన:

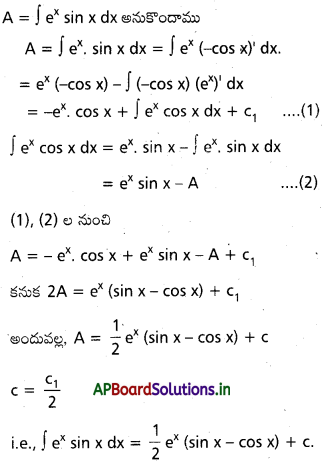
ప్రశ్న 28.
a,b,c  లు వాస్తవ సంఖ్లు b ≠ 0 అయితే R మీద ∫ e^ax cos (b x+c) dx ను గణించండి.
సాధన:
A=∫ e^ax cos (b x+c) d x అనుకొందాం
విభాగ సమాకలన సూత్రం నుండి

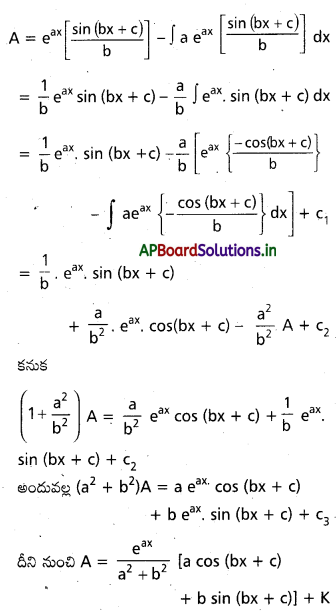
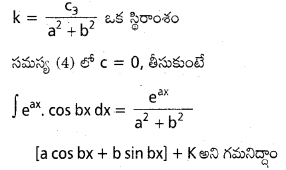
ప్రశ్న 29.
(-1,1) మీద ∫tan^-1 \(\sqrt{\frac{1-x}{1+x}} dx\) ను గణించండి.
సాధన:

ప్రశ్న 30.
x ∈ I ⊂ R\{2nπ : n∈ Z} మీద \(\int e^x\left(\frac{1-\sin x}{1-\cos x}\right)\) dx ను గణించండి.
సాధన:

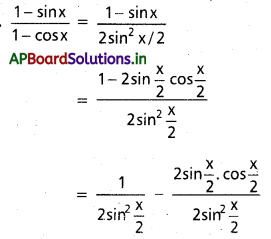
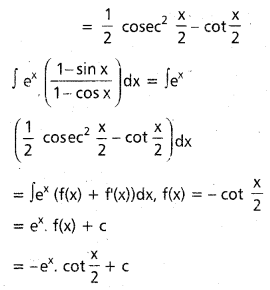
ప్రశ్న 31.
I ⊂ R\(-1,1) మీద
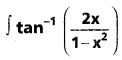dx ను గణించండి.

సాధన:

ప్రశ్న 32.
m వాస్తవ సంఖ్య అయితే (-1,1) మీద \(\int x^2 \frac{\exp \left(m \sin ^{-1} x\right)}{\sqrt{1-x^2}}\) dx ను కనుక్కోండి.
ఇక్కడ, {y}=e², Y ∈ R
సాధన:

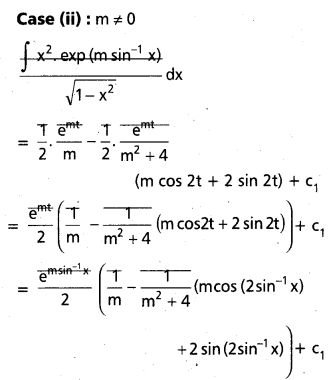
ప్రశ్న 33.
ను గణించండి.
సాధన:

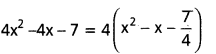
ప్రశ్న 34.
∫ \(\frac{d x}{5-2 x^2+4 x}\) ను కనుక్కోండి
సాధన:

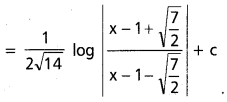
ప్రశ్న 35.
∫ \(\frac{d x}{x^2+x+1}\) ను గణించండి.
సాధన:

ప్రశ్న 36.
∫ \(\frac{d x}{\sqrt{x^2+2 x+10}}\) ను గణించండి.
సాధన:

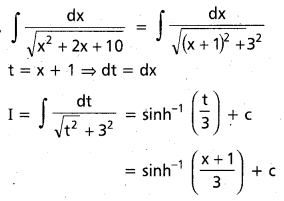
ప్రశ్న 37.
∫ \(\frac{d x}{\sqrt{1+x-x^2}}\) ను గణించండి.
సాధన:

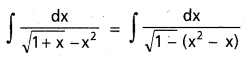
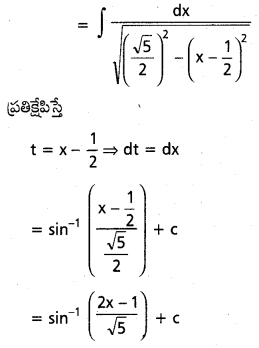
ప్రశ్న 38.
∫ \(\sqrt{3+8 x-3 x^2}\) dx ను గణించండి.
సాధన:

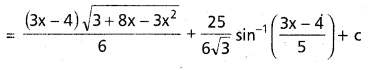
ప్రశ్న 39.
∫ \(\frac{x+1}{x^2+3 x+12}\) dx ను గణించండి.
సాధన:

ప్రశ్న 40.
∫ (3x -2) \(\sqrt{2 x^2-x+1}\) ను గణించండి.
సాధన:
(3 x-2)=A(4 x-1)+B అనుకుందాము
గుణకాలను సమానం చేయగా 3=4A
A=\(\frac{3}{4}\)
స్థిరపదాలు సమానం చేయగా – 2 = – A + B
B=-2+A=-2+\(\frac{3}{4}\)

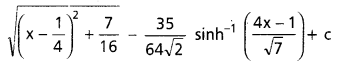
ప్రశ్న 41.
∫ \(\frac{2 x+5}{\sqrt{x^2-2 x+10}}\) dx ను గణించండి.
సాధన:

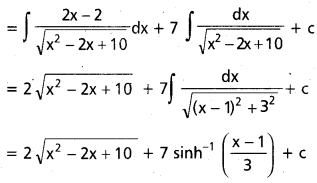
ప్రశ్న 42.
∫ \(\frac{d x}{5+4 \cos x}\) ను గణించండి.
సాధన:

ప్రశ్న 43.
∫ \(\frac{d x}{3 \cos x+4 \sin x+6}\) ను గణించండి.
సాధన:

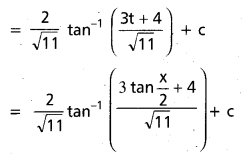
ప్రశ్న 44.
∫ \(\frac{d x}{d+e \tan x}\) ను కనుక్కోండి.
సాధన:

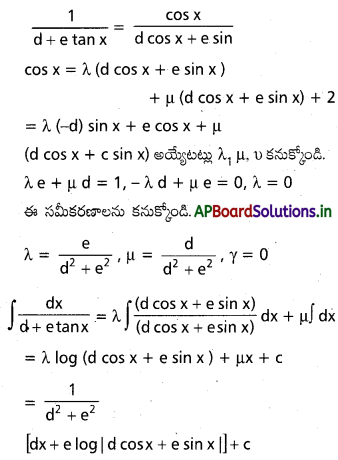
ప్రశ్న 45.
∫ \(\frac{\sin x}{d \cos x e \sin x}\) dx ∫ \(\frac{\cos x}{d \cos x+e \sin x}\)dx ను గణించండి.
సాధన:

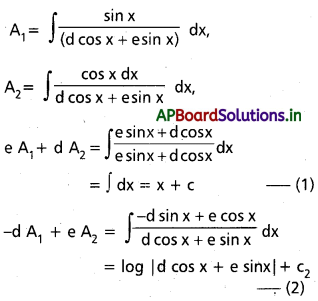
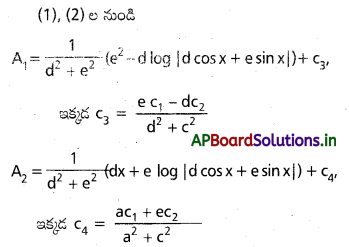
ప్రశ్న 46.
∫ \(\frac{\cos x+3 \sin x+7}{\cos x+\sin x+1}\) dx ను గణించండి.
సాధన:

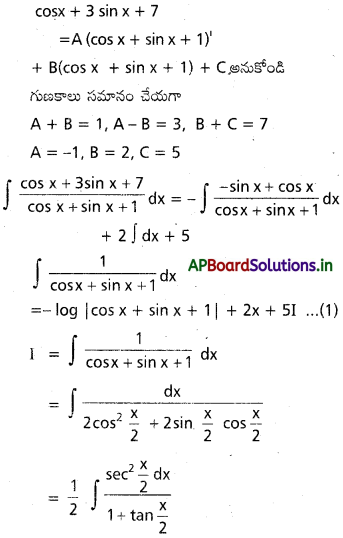
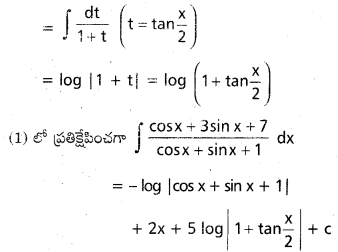
ప్రశ్న 47.
∫ \(\frac{x^3-2 x+3}{x^2+x-2}\) dx ను గణించండి.
సాధన:

ప్రశ్న 48.
∫ \(\frac{d x}{x^2-81}\) ను కనుక్కోండి.
సాధన:

ప్రశ్న 49.
∫ \(\frac{2 x^2-5 x+1}{x^2\left(x^2-1\right)}\) dx ను కనుక్కోండి.
సాధన:

ప్రశ్న 50.
∫ \(\frac{3 x-5}{x\left(x^2+2 x+4\right)}\) dx ను కనుక్కోండి.
సాధన:

ప్రశ్న 51.
∫ \(\frac{2 x+1}{x\left(x^2+4\right)^2}\) dx ను కనుక్కోండి.
సాధన:

ప్రశ్న 52.
∫ x³ e^5x dx ను గణించండి.
సాధన:

ప్రశ్న 53.
∫ sin⁴ x dx ను గణించండి.
సాధన:

ప్రశ్న 54.
∫ tan⁶ x dx ను గణించండి.
సాధన:

ప్రశ్న 55.
∫ sec ⁶ x dx ను గణించండి.
సాధన: