AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు

Students get through AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు which are most likely to be asked in the exam.

AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు

ప్రశ్న 1.
\(\int_1^2 x^5\) dx ను గణించండి.
సాధన:
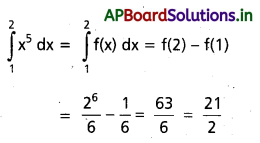
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 1

ప్రశ్న 2.
\(\int_0^a \sin\) x dx ను గణించండి.
సాధన:
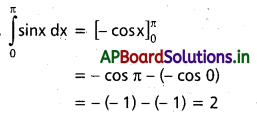
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 2

ప్రశ్న 3.
\(\int_0^a \frac{d x}{x^2+a^2}\) ను గణించండి.
సాధన:
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 3

ప్రశ్న 4.
\(\int_1^4 x \sqrt{x^2-1}\) ను గణించండి.
సాధన:
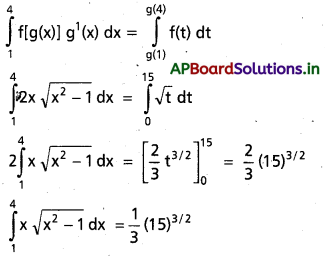
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 4

ప్రశ్న 5.
\(\int_0^2 \sqrt{4-x^2}\) dx విలువను గణించండి.
సాధన:
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 5

ప్రశ్న 6.
\(\int_0^{16} \frac{x^{1 / 4}}{1+x^{1 / 2}}\) dx ను గణించండి.
సాధన:
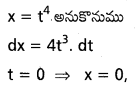
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 6

ప్రశ్న 7.
\(\int_{-\pi / 2}^{\pi / 2} \sin |x|\)ను గణించండి.
సాధన:
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 8

ప్రశ్న8.
\(\int_0^{\pi / 2} \sin ^n x d x=\int_0^{\pi / 2} \cos ^n x\)dx అని చూపండి.
సాధన:
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 9

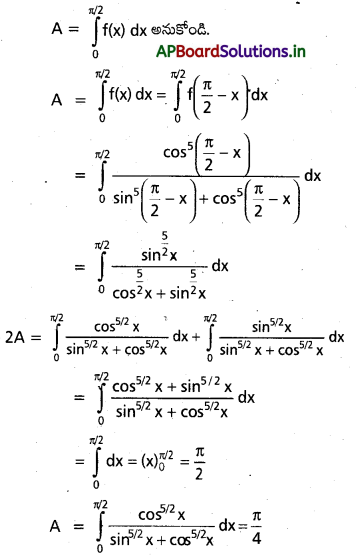
ప్రశ్న 9.
\(\int_0^{\pi / 2} \frac{\cos ^{5 / 2} x}{\sin ^{5 / 2} x+\cos ^{5 / 2} x}\) ను గణించండి.
సాధన:
\(f(x)=\frac{\cos ^{5 / 2} x}{\sin ^{5 / 2} x+\cos ^{5 / 2} x}\) dx అనుకోండి.
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 13

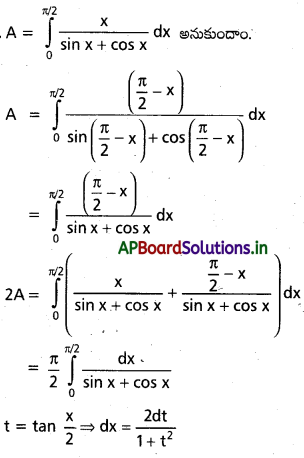
ప్రశ్న 10.
\(\int_0^{\pi / 2} \frac{x}{\sin x+\cos x} d x=\frac{\pi}{2 \sqrt{2}} \log (\sqrt{2}+1)\) అని చూపండి.
సాధన:
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 12

ప్రశ్న 11.
\(\int_{\pi / 6}^{\pi / 3} \frac{\sqrt{\sin x}}{\sqrt{\sin x}+\sqrt{\cos x}}\) dx ను గణించండి.
సాధన:

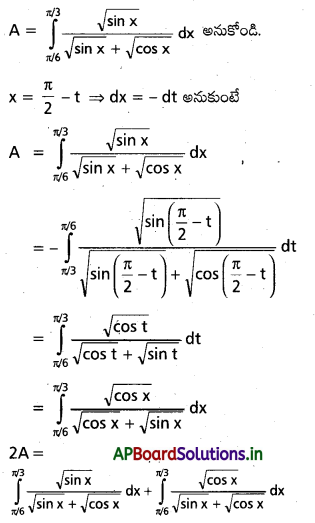
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 15

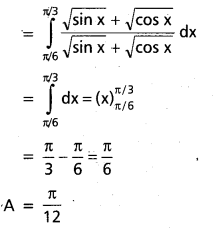
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 16

ప్రశ్న 12.
\(\int_{-a}^a\left(x^2+\sqrt{a^2-x^2}\right)\) ను కనుక్కోండి.
సాధన:
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 18

ప్రశ్న 13.
\(\int_0^\pi \frac{x \sin x}{1+\sin x}\) dx కనుక్కోండి.
సాధన:
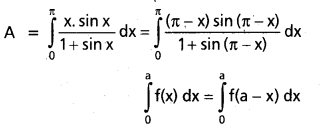
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 19

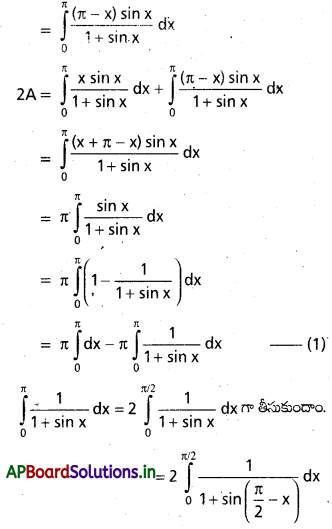
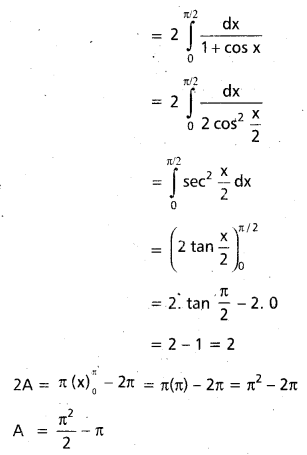
ప్రశ్న 14.
\(\int_0^{\pi / 2} x \sin x\) dx ను గణించండి.
సాధన:
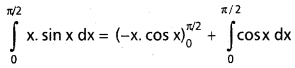
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 22

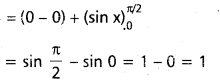
ప్రశ్న 15.
అవది వెుత్తం నిశ్చిత నమాకలనిని కనుక్కొనే పద్ధతినుపయోగించి \(\lim _{n \rightarrow \infty} \sum_{i=1}^n \frac{1}{n}\left[\frac{n-i}{n+i}\right]\) కనుక్కోండి.
సాధన:
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 24

ప్రశ్న 16.
అవధి మొత్తంగా నిశిళిత సమాకలనిని కనుక్కొనే పద్ధతి నుపయోగించి
\(\lim _{n \rightarrow \infty} \frac{2^k+4^k+6^k+\ldots \ldots+(2 n)^k}{n^{k+1}}\)
సాధన:
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 25

ప్రశ్న 17.
\(\lim _{n \rightarrow \infty}\left[\left(1+\frac{1}{n}\right)\left(1+\frac{2}{n}\right) \ldots\left(1+\frac{n}{n}\right)\right]^{\frac{1}{n}}\) కనుక్కోండి.
సాధన:
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 26

ప్రశ్న 18.
f: R → R అవిచ్ఛిన్న ఆవర్తన ప్రమేయం. దీనికి T ఒక ఆవర్తనం అయితే ప్రతి ధన హృా్ణాంకం n కి \(\int_0^{n T} f(x) d x=n \int_0^T f(x)\) dx అని చూపండి.
సాధన:
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 27

∴ x =m + 1 కు ఫలితము నిజము.
గణితాను గమన సిద్ధాంతం ప్రకారం ధన పూర్ణాంక విలువలన్నింటికి ఫలితము నిజము.

ప్రశ్న 19.
(i) \( \int_0^{\pi / 2} \sin ^4 x \)dx
(ii) \(\int_0^{\pi / 2} \sin ^7 x \)dx
(iii) \(\int_0^{\pi / 2} \cos ^8 x \) dx ను కనుక్కోండి.
సాధన:
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 29

ప్రశ్న 20.
\(\int_0^a \sqrt{a^2-x^2}\)
సాధన:
x= a sinθ dx= acosθ . dθ అనుకుంటే
θ = 0=,x = 0,x= a=θ = π/2
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 30

ప్రశ్న 21.
కింది నిశ్చిత సమాకలనులను గణించండి.
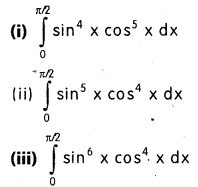
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 31
సాధన:

ప్రశ్న 22.
\(\int_0^{2 \pi} \sin ^4 x \cos ^6 x\) ను కనుక్కోండి.
సాధన:
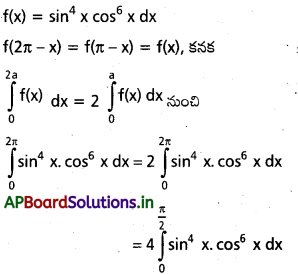
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 33

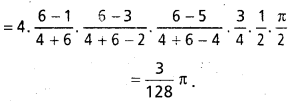
ప్రశ్న 23.
\(\int_{-\pi / 2}^{\pi / 2} \sin ^2 x \cos ^4\)xdx కనుక్కోండి.
సాధన:
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 35

ప్రశ్న 24.
\(\int_0^\pi x \sin ^7 x \cos ^6\)x dx కనుక్కోండి.
సాధన:
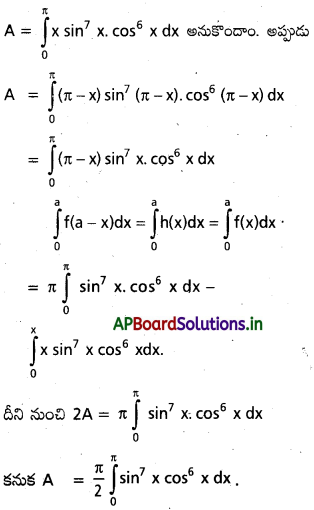
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 36

ప్రశ్న 25.
\(\int_{-a}^a x^2\left(a^2-x^2\right)^{3/2}\) dx కనుక్కోండి.
సాధన:
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 38

ప్రశ్న 26.
\(\int_0^1 x^{3 / 2} \sqrt{1-x}\) dx కనుక్కోండి.
సాధన:
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 39

ప్రశ్న 27.
[0,2 π] ల f(x)=sin x వక్రం క్రింది వైశాల్యాన్ని కనుక్కోండి.
సాధన:
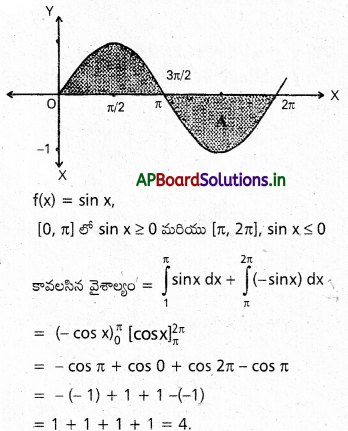
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 40

ప్రశ్న 28.
[0,2 π] అంతరంలో f(x)=cos x వక్రం క్రింది వైశాల్యాన్ని కనుక్కోండి.
సాధన:
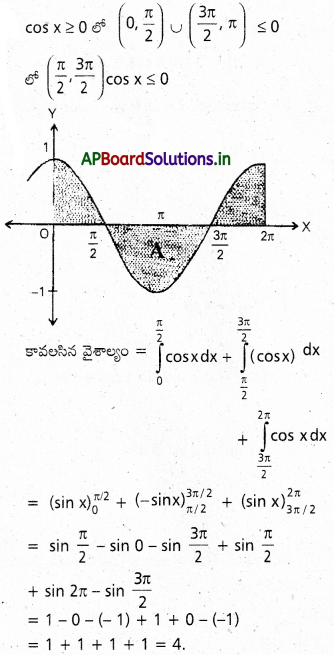
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 41

ప్రశ్న 29.
y=x² పరావలయంతోను, x- అక్షం, x=-1, x = 2 రేఖలతో పరిబద్ధపైన ప్రదేశం వైలాల్యం కనుక్సోండి.
సాధన:
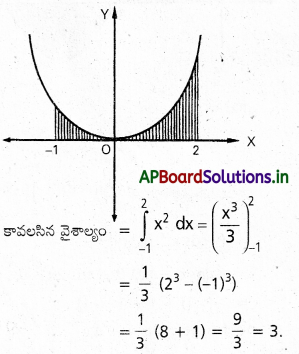
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 42

ప్రశ్న 30.
y=0 రేఖ, y=x²-4 x+3 పరావలయాల మధ్య అంతర్లిఖితమైన ప్రదేశ వైశాలృం కనుక్కోండి.
సాధన:
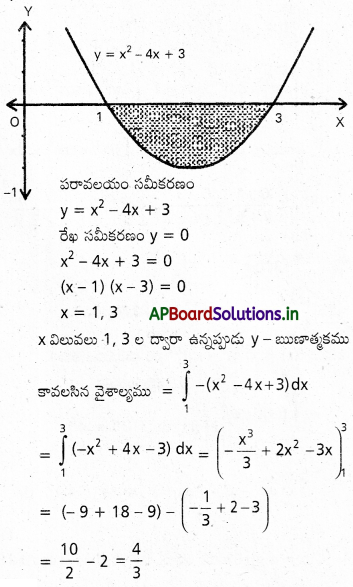
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 43

ప్రశ్న 31.
y = sin x, y=cos x వక్రాల రెండు వరుస ఖండన బిందువుల మధ్య పరిబద్ధమైన ప్రదేశం వైశాల్లం కనుక్కోండి.
సాధన:
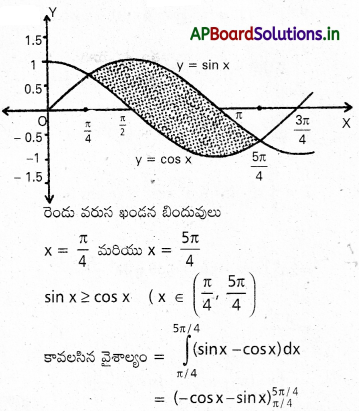
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 44

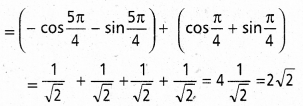
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 45

ప్రశ్న 32.
y=sin x, y=cos x, x – అక్షంతో పరిబద్ధమైన ఒక వక్రీయరేఖీయ త్రిభజం వైశాల్యం కనుక్కోండి.
సాధన:
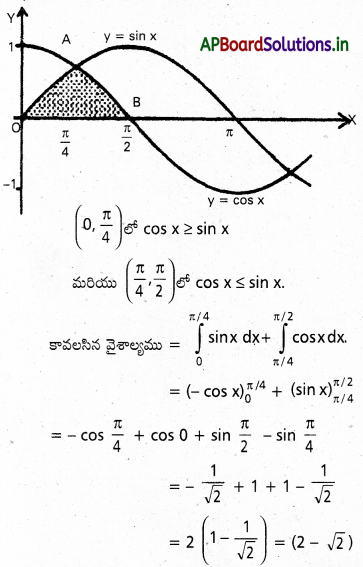
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 46

ప్రశ్న 33.
సమాకలన ప్రాథమిక సిద్ధాంతం ఉపయోగించి ఆధారం b, ఉన్నతి a గల లంబకోణ త్రిభాజం వైశాల్యం గణించండి.
సాధన:
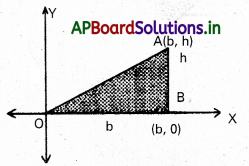
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 47
O A B లంబకోణ (తిభుజములు ∠B=90°
‘O’ ను మూల బిందువుగాను, OB ని X – అక్షంగా తీసు కుందాం.
O B=b మరియ A B=h, అయితే A నిరూపకాలు (b, h)
OA సథీకరణం y=\(\frac{h}{b}\) x
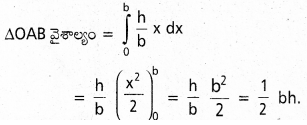
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 48
ప్రశ్న 34.
y²-1=2 x, x=0 వక్రాల మధ్య వైశాల్యం కనుక్కోండి.
సాధన:

ప్రశ్న 35.
y=3 x, y=6x – x² వక్రాలతో ఆవృతమైన వైశాల్యం కనుక్కోండి.
సాధన:
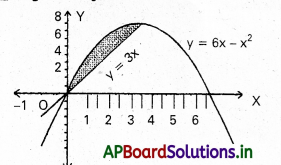
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 50
y=3 x రేఖ పరావలయాన్ని ఖండిస్తుంది.
y=6 x-x²
3 x=6 x-x²
x²-3 x=0
x(x-3)=0
x=0 text లేదా 3
కావలసిన వైశాల్యము= \(\int_0^3\left(6 x-x^2-3 x\right)\) dx
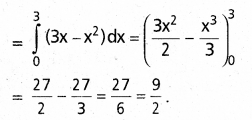
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 51

ప్రశ్న 36.
y=x²-5 x, y=4-2 x లతో ఆవృతమైన వైశాల్లం కనుక్కోండి.
సాధన:
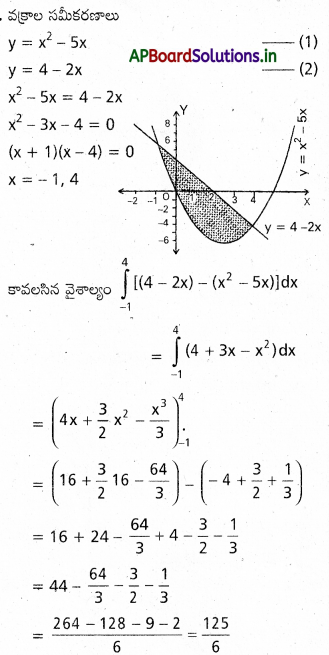
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 52
ప్రశ్న 37.
y=x², y=\(\sqrt{x}\), x ≥ 0 వక్రాలతో పరిబద్ధమైన వైశాల్యం కనుక్కోండి.
సాధన:

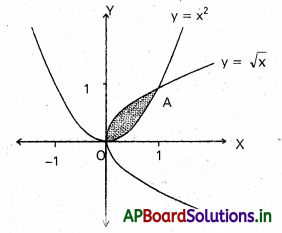
ప్రశ్న 38.
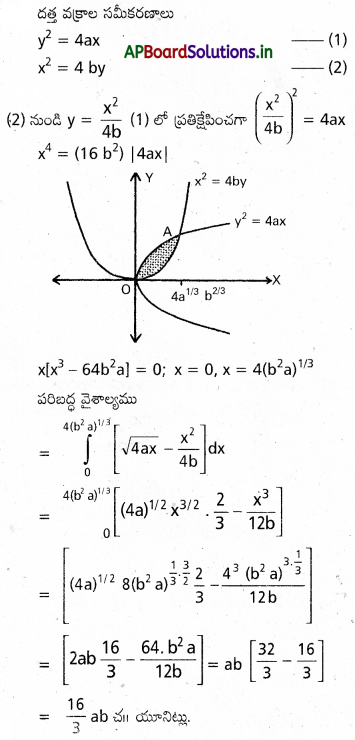
y²=4 a x, x²=4 b y(a>0, b>0) వక్రాల మధ్య పరిబద్ధమైన వైశాల్యం కనుక్కోండి.
సాధన:
AP Inter 2nd Year Maths 2B Important Questions Chapter 7 నిశ్చిత సమాకలనులు 55