AP Inter 2nd Year Maths 2B Important Questions Chapter 5 అతిపరావలయం

Students get through AP Inter 2nd Year Maths 2B Important Questions Chapter 5 అతిపరావలయం which are most likely to be asked in the exam.

AP Inter 2nd Year Maths 2B Important Questions Chapter 5 అతిపరావలయం

ప్రశ్న 1.
క్రింది అతిపరావలయాలకు కేంద్రం, ఉత్కేంద్రత, నాభులు, నియతరేఖలు నాఖిలంబం పొడవు కనుక్కోండి.
(i) 4 x²-9 y²-8 x-32=0
(ii) 4(y+3)² -9(x-2)²=1
సాధన:
(i) 4 x²-9 y²-8 x-32=0 అతిపరావలయం సమీకరణ

ప్రశ్న 2.
ఒక అతిపరావలయం, సంయుగ్మ అతిపరావలయాల ఉత్రేంద్రతలు వరుసగా e, e₁ అయతే \(\frac{1}{e^2}+\frac{1}{e_1^2}\)=1 అనిజాపండి.
సాధన:

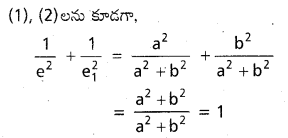
ప్రశ్న 3
(i) అతిపరావలయం \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) , lx+my+n=0 స్పర్శశేఖ అయితే, a²l²-b² m²=n² అని చూపండి.
(ii) అతిపరావలయం \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\)=15 lx+my=1 అఖిలంబరేఖ అయితే \(\frac{a^2}{l^2}-\frac{b^2}{m^2}=\left(a^2+b^2\right)^2\) అని చూపండి.
సాధన:
(i) స్పర్శ రేఖ సమీకరణం
l x+m y+n=0 ———– (1)
P(θ) వద్ద స్పర్శరేఖ సమీకరణము

ప్రశ్న 4.
x²– 4y²=12 అతిపరావలయానికి y=x-7 రేఖకు (i) సమాంతరంగాను (ii) లంబంగాను టంటే స్పర్శరేఖల సమీకరణాలను కనుక్కోండి.
సాధన:
అతిపరావలయ సమీకరణము 3x² -4y²=12
a² =4, b² =3

(i) y=x-7 కు సమాంతర స్పర్శరేఖ
m= స్పర్యరేఖ వాలు = 1
సమాంతర స్పర్శరేఖల సమీకరణము
y=m x ± \(\sqrt{a^2 m^2-b^2}\)
y=x ± \(\sqrt{4-3}\)=x±1

(ii) స్పర్యరేఖ y-x=7 కు లంబంగా ఉంటే
m = స్పర్ళరేఖ వాలు = -1
లంబ స్పర్యరేఖ సమీకరణము
y=(-1) x ± \(\sqrt{4(-1)^2-3}=-x \pm 1\)
x+y=± 1

ప్రశ్న 5.
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}\)=1 అతిపరావలయానికి రెండు లంబ స్పర్శరేఖల ఖండన బిందువు x²+y²=a²-b² పై ఉంటుందని చూపండి.
సాధన:
పరస్పర లంబంగా ఉన్న అతిపరావలయాల స్పర్శరేఖల ఖండన బిందువు P(x₁, y₁)
అతిపరాపలయ సమీకరణము \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
స్శర్శరేఖ సమీకరణాన్ని
\(y=m x \pm \sqrt{a^2 m^2-b^2} \) తీసుకొనవచ్చు.
ఈ స్పర్శరేఖ P(x₁, y₁) గుండా పోతుంది.

ప్రశ్న 6.
ఒక వృత్తం xy = 1 అనే లంబ అతిపరావలయాన్ని (x_r, y_r), r=1,2,3,4 అనే బిందువులలో ఖండిస్తుంది. x₁ x₂ x₃ x₄=y₁ y₂ y₃ y₄=1 అని చూపండి.
సాధన:
వృత్త సమీకరణాన్ని x²+y²=a² అనుకొందాం.
t ≠ 0 అయినప్పుడు \(\left(t, \frac{1}{t}\right)\), xy=1 మీద ఉంటుంది.
వృత్త, అతిపరావలయాల ఖండన బిందువుల నిరూపకాలు t^2+\frac{1}{t^2}=a^2 ను సంతృప్తిపరుస్తాయి.
అప్పుడు \(\mathrm{t}^4-\mathrm{a}^2 \mathrm{t}^2+1=0\)
⇒ t⁴+0 . t³-a² t²+0 . t+1=0
ఈ సమీకరణానికి మాలాలను t₁, t₂, t₃, t₄ అనుకొంటే t₁ t₂ t₃ t₄=1 అవుతుంది.

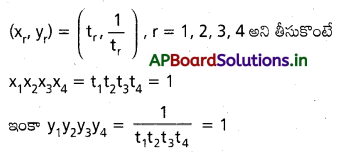
ప్రశ్న 7.
ఒక లంబ అతిపరావలయం మీద ఉండే నాలుగు బిందువులలో ఏ రెండింటినైనా కలుపగా వచ్చిన జ్యా, మిగిలిన రెండింటిని కలుపగా వచ్చిన జ్యాకు లంబంగా ఉంటూ, ఈ బిందువులను, అతిపరావలయ కేంద్రానికి కలుపగా వచ్చిన సరళరీఖలు, అ అతిపరావలయ అనంత స్రర్శరేఖలలో ఏదైనా ఒకదానితో α,β, γ, δ నిమ్నతలు కలిగి ఉంటే tan α, tan β, tan γ, tan δ =1 అని చూపండి.
సాధన:
లంబ అతిపరావలయం సవీకరణ x²-y²=a² అనుకొందాం. మూలబిందువు దృష్ట్ర X, Y అక్షాలను సవ్య దిశలో \(\frac{\pi}{4}\) కోణంతో జ్రమణం చేయగా x²-y²=a² క వచ్చే రూపాంతరం సమీకరణ రూపం x y=c² \(\left(t_r \neq 0\right),\left(c t_r, \frac{c}{t_r}\right)\), r=1,2,3,4 వక్రం మీద నాలుగు బిందువులు అనుకుందాం.

\(\stackrel{\leftrightarrow}{\mathrm{OA}}, \stackrel{\leftrightarrow}{\mathrm{OB}}, \stackrel{\leftrightarrow}{\mathrm{OC}}, \stackrel{\leftrightarrow}{\mathrm{OA}}{ }\) లు రెండవ అనంత స్పర్శరేఖ అయిన
y-అక్షం ధనదిశతో చేసే కోణాలను α,β, γ, δ అనుకొంటే, వాటి వాలులు వరుసగా cot α, cot β, cot γ, cot δ లవుతాయి. అప్వాడు కూడా tan α, tan β, tan γ, tan δ=(cot α cot β cot γ cot δ)^-1=1 అవుతుంది.