AP Inter 2nd Year Maths 2B Solutions Chapter 1 వృత్తం Ex 1(a)

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Chapter 1 వృత్తం Exercise 1(a) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2B Solutions Chapter 1 వృత్తం Exercise 1(a)

అభ్యాసం – 1(ఎ)

I.

ప్రశ్న 1.
వృత్త కేంద్రం C, వ్యాసార్థాలు r లు క్రింద ఇచ్చాం. C కేంద్రంగా, r వ్యాసార్ధంగా ఉంటే వృత్తాల సమీకరణాలను కనుక్కోండి.
i) C (2, 3), r = 4
సాధన:
వృత్త సమీకరణము
⇒ (x – h)² + (y – k)² = r²
⇒ (x – 2)² + (y + 3)² = 4²
x² – 4x + 4 + y² + 6y + 9 = 16
x² + y² – 4x + 6y – 3 = 0

ii) C = (-1, 2), r = 5
సాధన:
వృత్త సమీకరణము
(x + 1)² + (y – 2)² = 52
⇒ x² + 2x + 1 + y² – 4y + 4 = 25
⇒ x² + y² + 2x – 4y – 20 = 0

iii) C = (a, b); r = a + b
సాధన:
వృత్త సమీకరణము
(x − a)² + (y + b)² = r²
⇒ x² – 2xa + a² + y² + 2by + b² = (a + b)²
⇒ x² + y² – 2xa + 2by – 2ab

iv) C = (- a, – b); r = \(\sqrt{a^2-b^2}\) ([a] > [b])
సాధన:
వృత్త సమీకరణము
(x + a)² + (y + b)² = \(\left[\sqrt{a^2-b^2}\right]^2\)
⇒x² + y² + 2xa + 2yb + a² + b² = a² – b²
⇒ x² + y² + 2xa + 2yb + 2b² = 0

v) C = (cos α, sin α); r = 1.
సాధన:
వృత్త సమీకరణము
(x – cos α)² + (y – sin α)² = 1
x² + y² – 2x cos α – 2y sin α + sin²α + cos² α = 1
x² + y² – 2x cos α – 2y sin α = 0

vi) C = (-7, – 3); r = 4
సాధన:
వృత్త సమీకరణము
(x + 7)² + (y + 3)² = 42 = 16
x² + y² + 14x + 6y +49 + 9 = 16
⇒ x² + y² + 14x + 6y + 42 = 0

vii) C = \(\left(-\frac{1}{2},-9\right)\), r= 5
సాధన:
వృత్త సమీకరణము
\(\left(x+\frac{1}{2}\right)^2\) + (y + 9)² = 52
x² + x + \(\frac{1}{4}\) + y² + 18y + 81 = 25
x² + y² + x + 18y + 56 + \(\frac{1}{4}\) = 0
4x² + 4y² + 4x + 72y + 225 = 0

viii) C = \(\left(\frac{5}{2},-\frac{4}{3}\right)\), r = 6
సాధన:
వృత్త సమీకరణము
\(\left(x-\frac{5}{2}\right)^2\) + \(\left(y+\frac{4}{3}\right)^2\) = 6²
⇒ x² – 5x + \(\frac{25}{4}\) + y² + \(\frac{8}{3}\) y + \(\frac{16}{9}\) = 36
⇒ x² + y² – 5x + \(\frac{8}{3}\)y + \(\frac{25}{4}\) + \(\frac{16}{9}\) – 36 = 0
36 తో గుణించగా
36x² + 36y² – 180x + 96y + 225 + 64 – 1296 = 0
⇒ 36x² + 36у² – 180x + 96y – 1007 = 0

ix) C = (1, 7), r = \(\frac{5}{2}\)
సాధన:
వృత్త సమీకరణము
(x – 1)² + (y – 7)² = \(\left(\frac{5}{2}\right)^2\)
⇒ x² – 2x + 1+ y² – 14y + 49 = \(\frac{25}{4}\)
⇒ x² + y² – 2x – 14y + \(\frac{175}{4}\) = 0
4x² + 4y² – 8x – 56y + 175 = 0

x) C = (0, 0); r = 9.
సాధన:
వృత్త సమీకరణము
(x – 0)² + (y – 0)² = (9)²
x² + y² = 81

ప్రశ్న 2.
( – 4, – 3) కేంద్రంగా ఉంటూ మూలబిందువు గుండా పోయే వృత్త సమీకరణాన్ని కనుక్కోండి.
సాధన:
వృత్త సమీకరణం
(x – h)² + (y – k)² = r²; (h, k) = (- 4, – 3)
(x + 4)² + (y + 3)² = r²
వృత్తము మూలబిందువు గుండా పోతుంది.
∴ (0 + 4)² + (0 + 3)² = r² ⇒ 25 = r²
వృత్త సమీకరణము
(x + 4)² + (y + 3)² = 25
x² + y² + 8x + 6y = 0

ప్రశ్న 3.
(2, 3) కేంద్రంగా ఉంటూ (2, – 1) గుండా పోయే వృత్త సమీకరణాన్ని కనుక్కోండి.
సాధన:
C = (2, 3), P = (2, -1)
వ్యాసార్ధము CP = \(\sqrt{(2-2)^2+(3+1)^2}\) = 4
వృత్త సమీకరణము
(x – 2)² + (y – 3)² = 4²
x² + y² – 4x – 6y – 3 = 0

ప్రశ్న 4.
(0, 0) కేంద్రంగా ఉంటూ (-2, 3) గుండా పోయే వృత్త సమీకరణాన్ని కనుక్కోండి.
సాధన:
C = (0, 0), P = (-2, 3)
వ్యాసార్ధము = \(\sqrt{(0+2)^2+(0-3)^2}\)
= \(\sqrt{13}\)
వృత్త సమీకరణము
(x – 0)² + (y – 0)² = (\(\sqrt{13}\))²
x² + y² = 13

ప్రశ్న 5.
(- 3, 4) కేంద్రంగా ఉంటూ (3, 4) గుండా పోయే వృత్త సమీకరణాన్ని కనుక్కోండి.
సాధన:
వృత్త సమీకరణము
(x – h)² + (y – k)² = r²
కేంద్రం (h, k) = (-3, 4)
(x + 3)² + (y – 4)² = 12
వృత్తము (3, 4) గుండా పోతుంది.
(3 + 3)² + (4 – 4)² = r²
r² = 36
వృత్త సమీకరణము
(x + 3)² +(y – 4)² = 36
x² + 6x + 9 + y² – 8y + 18 – 36 = 0
x² + y² + 6x – 8y – 11 = 0

ప్రశ్న 6.
2x² + ay² – 3x + 2y – 1 = 0 25 సూచిస్తే a విలువను, వృత్త వ్యాసార్ధాన్ని కనుక్కోండి. (Mar. ’13)
సాధన:
ax² + 2hxy + by² + 2gx + 2fy + c = 0
వృత్త ‘సమీకరణాన్ని సూచిస్తే,
a = b, h = 0, g² + f² – c ≥0
2x² + ay² – 3x + 2y – 1 = 0.
a = 2, అయితే పై సమీకరణము వృత్తాన్ని సూచిస్తుంది.
x² + y² – \(\frac{3}{2}\) x + y – \(\frac{1}{2}\) = 0
2g = –\(\frac{3}{2}\) ; 2f = 1; C = –\(\frac{1}{2}\)
c = (g, – f) = \(\left(\frac{+3}{4}, \frac{-1}{2}\right)\)
వ్యాసార్ధం = \(\sqrt{g^2+f^2-c}=\sqrt{\frac{9}{16}+\frac{1}{4}+\frac{1}{2}}\)
= \(\frac{\sqrt{21}}{4}\) యూనిట్లు.

ప్రశ్న 7.
ax² + bxy + 3y² – 5x + 2y – 3 = 0 సూచిస్తే a, b ల విలువలు కనుక్కోండి. ఇంకా దీని వ్యాసార్థం, కేంద్రాన్ని కనుక్కోండి.
సాధన:
ax² + 2hxy + by² + 2gx + 2fy + c = 0
వృత్తాన్ని సూచిస్తే a = 3, h = 0
∴ ax² + bxy + 3y² – 5x + 2y – 30 = 0 వృత్తాన్ని సూచిస్తుంది.
∴b = 0, a = 3
3x² + 3y² – 5x + 2y – 3 = 0
x² + y² – \(\frac{5}{3}\)x + \(\frac{2}{3}\)y – 1 = 0
g = –\(\frac{5}{6}\) ; f = \(\frac{2}{6}\) ; c = -1
C = (-g, -f) = \(\left(\frac{5}{6},-\frac{1}{3}\right)\)
వ్యాసార్ధము = \(\sqrt{g^2+f^2-c}=\sqrt{\frac{25}{36}+\frac{1}{9}+1}\)
= \(\frac{\sqrt{65}}{6}\) యూనిట్లు.

ప్రశ్న 8.
x² + y² + 2gx + 2fy – 12 = 0 సమీకరణం (2, 3) కేంద్రంగా ఉండే వృత్తాన్ని సూచిస్తే, 9. f లను, వృత్త వ్యాసార్థాన్ని కనుక్కోండి. [May ’11]
సాధన:
వృత్త సమీకరణం
x² + y² + 2gx + 2fy – 12 = 0
కేంద్రం C (g, – f) = (2, 3)
కనుక g = 2, f = -3, c = -12
∴ వృత్త వ్యాసార్ధం (r) = \(\sqrt{g^2+f^2-c}\)
= \(\sqrt{(-2)^2+(-3)^2+12}\)
= \(\sqrt{4+9+12}=\sqrt{25}\) = 5 యూనిట్లు.

ప్రశ్న 9.
x² + y² + 2gx + 2fy = 0 సమీకరణం (-4,-3) కేంద్రంగా ఉండే వృత్తాన్ని సూచిస్తే g, f వృత్త వ్యాసార్థాలను కనుక్కోండి.
సాధన:
వృత్త సమీకరణం
x² + y² + 2gx + 2fy = 0
కేంద్రం C (g, f) = (-4, -3)
∴ g = 4, f = 3, c = 0
వ్యాసార్ధం = \(\sqrt{g^2+f^2-c}\)
= \(\sqrt{4^2+3^2-0}\)
= \(\sqrt{25}\) = 5 యూనిట్లు.

ప్రశ్న 10.
x² + y² – 4x + 6y + c = 0 సూచించే వృత్త వ్యాసార్ధం “6” అయితే “C” విలువ కనుక్కోండి.
సాధన:
వృత్త సమీకరణం
x² + y² – 4x + 6y + c = 0
ఇచ్చట 2g = – 4, 2f = 6, c = c
⇒ g = -2, f = 3, c = c
∴ వృత్త వ్యాసార్ధం (r) = 6
⇒ \(\sqrt{g^2+f^2-c}\) = 6
⇒ \(\sqrt{(-2)^2+(3)^2-c}\) = 6
⇒ 13 – c = 6²
⇒ c = 13 – 36 = -23

ప్రశ్న 11.
కింద ఇచ్చిన ప్రతి వృత్తపు కేంద్రం, వ్యాసార్థం కనుక్కోండి.
i) x² + y² – 4x – 8y – 41 = 0
సాధన:
దత్త సమీకరణాన్ని x² + y² + 2gx + 2fy + c = 0 తో పోల్చగా
2g = – 4, 2f = -8, c = -41,
g = – 2, f = – 4, c = -41
వ్యాసార్ధము = \(\sqrt{g^2+f^2-c}\)
= \(\sqrt{4+16+41}=\sqrt{61}\) యూనిట్లు
కేంద్రం = (-g, -f) = (2, 4)

ii) 3x² + 3y² – 5x – 6y + 4 = 0
సాధన:
వృత్త సమీకరణం 3x² + 3y³ – 5x – 6y + 4 = 0
⇒ x² + y² – \(\frac{5}{3}\)x – 2y + \(\frac{4}{3}\) = 0
ఈ సమీకరణాన్ని x² + y² + 2gx + 2fy + c = 0 తో పోల్చగా
2g = –\(\frac{5}{3}\) ; 2f = -2 ; C = \(\frac{4}{3}\)
⇒ g = –\(\frac{5}{6}\) ; f = -1 ; C = \(\frac{4}{3}\)
∴ వృత్త కేంద్రం C = (-g, -f) = \(\left(\frac{5}{6}, 1\right)\)

iii) 3x² + 3y² + 6x – 12y – 1 = 0
సాధన:
దత్త వృత్త సమీకరణం
3x² + 3y² + 6x – 12y – 1 = 0
⇒ x² + y² + 2x – 4y – \(\frac{1}{3}\)
సాధారణ సమీకరణం x² + y² + 2gx + 2fy + c = 0
తో పోల్చగా
2g = 2, 2f = -4, c = –\(\frac{1}{3}\)
⇒ g = 1, f = -2, c = –\(\frac{1}{3}\)
కేంద్రం C = (-g, -f) = (-1, 2)

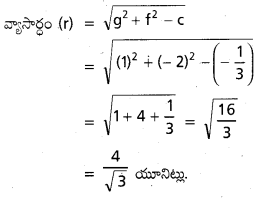
iv) x² + y² + 6x + 8y – 96 = 0
సాధన:
దత్త వృత్తన్నీ x² + y² + 2gx + 2fy + c = 0 తో పోల్చగా
2g = 6, 2f = 8, c = -96
g = 3, f = 4, c = -96
కేంద్రం C = (g, f) = (-3, -4)
వ్యాసార్ధం (r) = \(\sqrt{g^2+f^2-c}\)
= \(\sqrt{3^2+4^2-(-96)}\)
= \(\sqrt{9+16+96}=\sqrt{121}\)
= 11 యూనిట్లు.

v) 2x² + 2y² – 4x + 6y -3 = 0
సాధన:
వృత్త సమీకరణము
x² + y² – 2x + 3y – \(\frac{3}{2}\) = 0 ………….. (i)
x² + ² + 2gx + 2fy + c = 0 ……………. (ii)
(i) మరియు (ii) లను పోల్చగా C = \(\left(1,-\frac{3}{2}\right)\)
వ్యాసార్ధము = \(\sqrt{g^2+f^2-c}\)
= \(\sqrt{1+\frac{9}{4}+\frac{3}{2}}=\frac{\sqrt{19}}{2}\) యూనిట్లు.

vi) 2x² + 2y² – 3x + 2y – 1 = 0
సాధన:
వృత్త సమీకరణము
x² + y² – \(\frac{3}{2}\)x + y – \(\frac{1}{2}\) = 0
x\(\frac{1}{2}\) + y\(\frac{1}{2}\) + 2gx + 2fy + c = 0 పోల్చగా
C(g, f) = \(\left(\frac{3}{4},-\frac{1}{2}\right)\)
వ్యాసార్ధము = \(\sqrt{g^2+f^2-c}\)
= \(\sqrt{\frac{9}{16}+\frac{1}{4}+\frac{1}{2}}=\frac{\sqrt{21}}{4}\) యూనిట్లు.

vii) \(\sqrt{1+m^2}\) (x² + y²) – 2cx – 2mcy = 0
సాధన:
వృత్త సమీకరణము

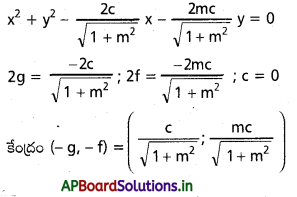
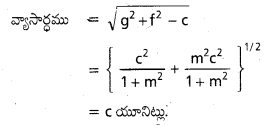
viii) x² + y² + 2ax – 2by + b² = 0
సాధన:
వృత్త సమీకరణము
x² + y² + 2gx + 2fy + c = 0
C = (-g, -f) (-a, b)
వ్యాసార్ధము = \(\sqrt{g^2+f^2-c}\)
= \(\sqrt{a^2+b^2-b^2}\) = a యూనిట్లు

ప్రశ్న 12.
కింది బిందువుల జతలు వ్యాసాగ్రాలుగా ఉన్న వృత్తాల -సమీకరణాలను కనుక్కోండి.
i) (1, 2), (4, 6)
సాధన:
(x₁, y₁), (x₂, y₂) లు వ్యాసాగ్రాలుగా గల వృత్త సమీకరణము
(x – x₁)(x – x₂) + (y – y₁) (y – y₂) = 0
⇒ (x – 1) (x – 4) + (y – 2) (y – 6) = 0
⇒ x² – 5x + 4 + y² – 8y + 12 = 0
⇒ x² + y² – 5x – 8y + 16 = 0

ii) (-4, 3); (3,-4)
సాధన:
(x₁, y₁), (x₂, y₂) లు వ్యాసాగ్రాలుగా గల వృత్త సమీకరణము
(x – x₁)(x – x₂) + (y – y₁) (y – y₂) = 0
కావలసిన వృత్త సమీకరణము
(x + 4) (x – 3) + (y – 3) (y + 4) = 0
x² + y² + x + y – 24 = 0

iii) (1, 2); (8, 6)
సాధన:
వృత్త సమీకరణము
(x – x₁)(x – x₂) + (y – y₁) (y – y₂) = 0
⇒ (x – 1) (x – 8) + (y – 2) (y – 6) = 0
x² + y² – 9x – 8y + 20 = 0

iv) (4, 2); (1, 5)
సాధన:
వృత్త సమీకరణము
(x – x₁)(x – x₂) + (y – y₁) (y – y₂) = 0
⇒ (x – 4) (x – 1) + (y – 2) (y – 5) = 0
x² + y² – 5x – 7y + 14 = 0

v) (7, -3); (3, 5)
సాధన:
వృత్త సమీకరణము
(x – x₁)(x – x₂) + (y – y₁) (y – y₂) = 0
⇒ (x – 7) (x – 3) + (y + 3) (y – 5) = 0
x² + y² – 10x – 2y + 6 = 0

vi) (1, 1); (2,-1)
సాధన:
వృత్త సమీకరణము
(x – x₁)(x – x₂) + (y – y₁) (y – y₂) = 0
⇒ (x – 1) (x – 2) + (y – 1) (y + 1) = 0
x² + y² – 3x + 1 = 0

vii) (0, 0); (8,5)
సాధన:
వృత్త సమీకరణము
(x – x₁)(x – x₂) + (y – y₁) (y – y₂) = 0
⇒(x – 0) (x – 8) + (y – 0) (y – 5) = 0
⇒ x² – 8x + y² – 5y = 0
⇒ x² + y² – 8x – 5y = 0

viii) (3, 1); (2,7)
సాధన:
వృత్త సమీకరణము
(x – x₁)(x – x₂) + (y – y₁) (y – y₂) = 0
(x – 3) (x – 2) + (y – 1) (y – 7) = 0
x² + y² – 5x – 8y + 13 = 0

ప్రశ్న 13.
కింద ఇచ్చిన వృత్తాలలోని ప్రతి వృత్తానికి పరామితీయ సమీకరణాలను రాయండి.
i) x² + y² = 4
సాధన:
C (0, 0), r = 2
పరామితీయ సమీకరణాలు
x = gr cos θ = 2 cos θ
y = – b + r sin θ = 2 sin θ, 0 ≤ θ < 2π

ii) 4(x² + y²) = 9
సాధన:
x² + y² = \(\frac{9}{4}\)
C (0, 0), r = \(\frac{3}{2}\)
పరామితీయ సమీకరణాలు
x = \(\frac{3}{2}\) cos θ, y = \(\frac{3}{2}\) sin θ, 0 ≤ θ < 2π

iii) 2x² + 2y² = 7
సాధన:
x² + y² = \(\frac{7}{2}\)
C (0, 0), r = \(\sqrt{\frac{7}{2}}\)
పరామితీయ సమీకరణాలు
x = \(\sqrt{\frac{7}{2}}\) cos θ, y = \(\sqrt{\frac{7}{2}}\) sin θ, 0 ≤ θ < 2π

iv) (x – 3)² + (y – 4) ² = 82 [A.P. Mar’ 16, Mar ’11]
సాధన:
కేంద్రం (3, 4), r = 8
పరామితీయ సమీకరణాలు
x = 3 + 8 cos θ, y = 4 + 8 sin θ, 0 ≤ θ < 2π

v) x² + y² – 4x – 6y – 12 = 0
సాధన:
కేంద్రం (2,3), r = \(\sqrt{4+9+12}\) = 5
పరామితీయ సమీకరణాలు
x = 2 + 5 cos θ, y = 3 + 5 sin θ, 0 ≤ θ < 2π.

vi) x² + y² – 6x + 4y – 12 = 0
సాధన:
కేంద్రం (3, – 2), r = \(\sqrt{9+4+12}\) = 5
పరామితీయ సమీకరణాలు
x = 3 + 5 cos θ, y = -2 + 5 sin θ, 0 ≤ θ < 2π

II.

ప్రశ్న 1.
A, B బిందువుల x నిరూపకాలు x² + 2ax – b² = 0 కు మూలాలు, y నిరూపకాలు y ² + 2py – q²= 0 కు మూలాలు అయితే A, B లు వ్యాసాగ్రాలుగా ఉండే వృత్త సమీకరణాన్ని కనుక్కోండి..
సాధన:
వృత్త సమీకరణము
(x – x₁) (x – x₁) + (y – y₁) (y – y₁) = 0
x² – x(x₁ + x₂) + x₁x₂ + y² – y (y₁ + y₂) + y₁y₂ = 0
x₁, x₂ లు x² + 2ax = b² = 0, కు మూలాలు
y₁, y₂ లు y² + 2py – q² = 0, కు మూలాలు
x₁ + x₂ = – 2a
x₁x₂ = – b²

y₁ + y₂ = – 2p
y₁y₂ = – q²

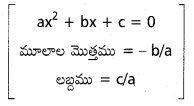
వృత్త సమీకరణము
x² – x (-2a) – b² + y² – y ( – 2p) – q² = 0
x² + 2xa + y² + 2py – b² – q² = 0

ప్రశ్న 2.
i) A (3, -1) బిందువు x² + y² – 2x + 4y = 0 వృత్తం పై బిందువని చూపి, A ద్వారా పోయే వ్యాసం రెండో చివరి బిందువును కనుక్కోండి.
సాధన:
వృత్త సమీకరణము
x² + y² – 2x + 4y = 0 ……………… (i)
A(3, – 1); B(x₁, y₁)
(i) లో A ప్రతిక్షేపించగా
(3)² + (-1)² – 2(3) + 4 (-1) = 0
∴ A వృత్తం మీద ఉన్నది.
C (- g, – f)
C = (1, -2)

C వృత్త కేంద్రం
AB మధ్య బిందువు.
\(\frac{x_1+3}{2}\) = 1
x₁ = -1

\(\frac{y_1-1}{2}\) = -2
y₁ = -3
B(x₁, y₁) = (-1, -3)

ii) A (-3, 0) బిందువు x² + y² + 8x + 12y + 15 = 0 వృత్తంపై బిందువుని చూపి, A ద్వారా పోయే వ్యాసం రెండోచివరి బిందువును కనుక్కోండి.
సాధన:
A ( 3, 0) ను ప్రతిక్షేపించగా
x² + y² + 8x + 12y + 15 = 0
(-3)² + (0)² – 8 × 3 + 12 × 0 + 15
9 – 24+ 15 = 0
∴ (- 3, 0) ఒక వ్యాసాగ్రము
A (- 3, 0)
C (-4, -6)
B (x₁, y₁)
\(\frac{x_1+(-3)}{2}\) = -4
x₁ = -5

\(\frac{y_1+0}{2}\) = -6
y₁ = -12
∴ రెండవ కొన (-5, – 12)

ప్రశ్న 3.
(2, -3), (−4, 5) బిందువుల గుండా పోయే వృత్త కేంద్రం 4x + 3y + 1 = 0 రేఖపై ఉంటే ఆ వృత్త సమీకరణాన్ని కనుక్కోండి.
సాధన:
x² + y² + 2gx + 2fy + c = 0 …………….. (i)
సమీ. (i) (2, – 3), (-4, 5) ల గుండా వృత్తం పోతుంది.
∴ 4 + 9 + 4g – 6f + c = 0 ……………. (ii)
16 + 25 – 8g + 10f + c = 0 …………….. (iii)
(iii) – (ii) చేయగా
28 – 12g + 16f = 0
(లేదా) 3g – 4f = 7
కేంద్రం (- g, – f) రేఖ 4x + 3y + 1 = 0 మీద ఉంది.
∴ 4(g) + 3(f) + 1 = 0
3g – 4f – 7 = 0
సాధించగా f = – 1
g = 1
(ii) లో f, g విలువలు ప్రతిక్షేపించగా
4 + 9 + 4(1) – 6 (- 1) + c = 0, C = – 23
x² + y² + 2x – 2y – 23 = 0 ఇది కావలసిన వృత్త సమీకరణము.

ప్రశ్న 4.
(4, 1), (6, 5) బిందువుల గుండా పోయే వృత్త కేంద్రం 4x + 3y – 24 = 0 రేఖపై ఉంటే ఆ వృత్త సమీకరణాన్ని కనుక్కోండి. [A.P. Mar. ’16]
సాధన:
x² + y² + 2gx + 2fy + c = 0 వృత్తం (4, 1)
మరియు (6,5) ల గుండా పోతుంది.
4² + 1² + 2g(4) + 2f(1) + c = 0 ………….. (i)
6² + 5² + 2g(6) + 2f(5) + c = 0 …………….. (ii)
కేంద్రం 4x + 3y – 24 = 0 మీద ఉంది
∴ 4(g) + 3(-f) – 24 = 0 …………… (iii)
(ii) – (i) లు సాధించగా
44 + 4g + 8f = 0 ………………… (iv)
(iii) మరియు (iv) లు సాధించగా
f = – 4, g = -3, c = 15
∴ కావలసిన వృత్త సమీకరణము.
x² + y² – 6x – 8y + 15 = 0

ప్రశ్న 5.
x² + y² – 6x – 4y – 12 = 0 వృత్తంలో సకేంద్రీయమై ( – 2, 14) బిందువు గుండా పోయే వృత్త సమీకరణాన్ని కనుక్కోండి.
సాధన:
x² + y² – 6x – 4y – 12 = 0 …………………. (i)
C = (-g, – f) = (3, 2)
(i) లోని సకేంద్రీయ వృత్త సమీకరణము
(x – 3)² + (y – 2)² = r²
(-2, 14) గుండా పోతుంది.
(-2, -3)² + (14 – 2)² = r²
∴ 169 = r²
కావలసిన వృత్త సమీకరణము
(x – 3)² + (y – 2)² = 169
x² + y² – 6x – 4y – 156 = 0

ప్రశ్న 6.
వృత్త కేంద్రం X – అక్షంపై ఉంటూ (-2, 3), (4, 5) బిందువుల గుండా పోయే వృత్త సమీకరణాన్ని కనుక్కోండి.
సాధన:
వృత్త సమీకరణం
x² + y² + 2gx + 2fy + c = 0 …………… (i) అనుకుందాం.
దాని కేంద్రం C(-g, -f), x – అక్షంపై వున్నది కనుక
f = 0 ………………… (1)
∴ వృత్త సమీకరణము x² + y² + 29x + 2fy + c = 0
ఇది (-2, 3), (4, 5) ల గుండా పోతుంది కనుక
(-2)² + (3)² + 2g(-2) + c = 0
⇒ -4g + c = -13 …………… (2)
(4)² + (5)² + 2g(4) + c = 0

ప్రశ్న 7.
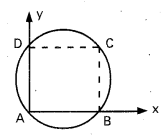
ABCD ఒక చతురస్రం అయితే దీని శీర్షాలు A, B, C, D లు చక్రీయాలు అని చూపండి.
సాధన:
AB = a, AD = a
A (0, 0), B(0, a), D (a, 0)
వృత్త సమీకరణము
x² + y² + 2gx + 2fy + c = 0
వృత్తం A, B, D ల గుండా పోతుంది.
A: 0+0+2g(0) + 2f(0) + c = 0
C = 0
B: 0 + a² + 2g(0) + 2fa + 0 = 0
f = –\(\frac{a}{2}\)
ఇదే విధంగా g = – \(\frac{a}{2}\)
కావలసిన వృత్త సమీకరణము
x² + y² – ax – ay = 0
C నిరూపకాలు (a, a)
a² + a² – a² – a²= 0
⇒ A, B, D ల గుండా పోయే వృత్తం మీద C ఉంది.
∴ A, B, C, D లు చక్రీయాలు.

III.

ప్రశ్న 1.
కింద ఇచ్చిన బిందువుల గుండా పోయే ప్రతి వృత్త సమీకరణాన్ని కనుక్కోండి.
i) (3, 4); (3, 2); (1, 4)
సాధన:
వృత్త సమీకరణము
x² + y² + 2gx + 2fy + c = 0
దత్త బిందువులు వృత్తం మీద ఉన్నాయి కనుక
9 + 16 + 6g + 8f + c = 0. …………………. (i)
9 + 4 + 6g + 4f + c = 0 …………………… (ii)
1 + 16 + 2g + 8f + c = 0 …………………. (iii)
(ii) నుండి (i) తీసివేయగా
– 12 – 4f = 0 (లేదా) f = -3
(ii) నుండి (iii) తీసివేయగా
-4 + 4g – 4f = 0
g – f = 1 ⇒ g = – 2
(i) లో g, f ల విలువలు ప్రతిక్షేపించగా
25 + 6 (-2) + 8 (-3) + c = 0
c = 11
కావలసిన వృత్త సమీకరణము
x² + y² – 4x – 6y + 11 = 0

ii) (1, 2); (3,-4); (5, 6) [T.S. Mar. ’16]
సాధన:
వృత్త సమీకరణము
x² + y² + 2gx + 2fy + c = 0
1 + 4 + 2gx + 4fy + c = 0 …………….. (i)
9 + 16 + 6g – 8f + c = 0 ………………… (ii)
25 + 36 + 10g – 12f + c = 0 …………….. (iii)
(ii) – (i) చేయగా
20 + 4g – 12f=0
(లేదా) 5 + g – 3f = 0 ……………. (iv)
(iii) – (ii) చేయగా
36 + 4g – 4f = 0
(లేదా) 9 + g – f = 0 ……………… (v)
(v) మరియు (iv) ను సాధించగా
f = – 2, g = – 11, c = 25
కావలసిన వృత్త సమీకరణము
x² + y² – 22x – 4y + 25 = 0

iii) (2, 1); (5, 5); (- 6, 7)
సాధన:
వృత్త సమీకరణము
x² + y ² + 2gx + 2fy + c = 0
4 + 1 + 4g + 2 + c = 0 ……………. (i)
25 + 25 + 10g + 10f + c = 0 ……………… (ii)
36 + 49 – 12g + 14f + c = 0 …………………. (iii)
(ii) – (i) చేయగా
45 + 6g + 8f = 0 ………………….. (iv)
(iii) – (ii) చేయగా
35 – 22g + 4f = 0 …………………… (v)
(iv) మరియు (v) సాధించగా
g = \(\frac{1}{2}\) ; f = – 6; c = 5
కావలసిన వృత్త సమీకరణము
x² + y² + x – 12y + 5 = 0

iv) (5, 7); (8, 1); (1, 3)
సాధన:
వృత్త సమీకరణము
x² + y² + 2gx + 2fy + c = 0
25 +49 + 10g + 14f + c = 0 …………………. (i)
64 + 1 + 16g + 2f + c = 0 ………………… (ii)
1 + 9 + 2g + 6f + c = 0 ……………….. (iii)
(ii) – (i) చేయగా
9 + 6g – 12f = 0 ………………….. (iv)
(లేదా) 2g – 4f – 3 = 0
(iii) – (ii) చేయగా
-55 – 14g + 4f = 0 ………………… (v)
(v) మరియు (iv) సాధించగా
g = \(\frac{-29}{6}\), f = \(\frac{-19}{6}\), c = \(\frac{56}{3}\)
∴ కావలసిన వృత్త సమీకరణము
x² + y² – \(\frac{29}{3}\)x – \(\frac{19}{3}\)y + \(\frac{56}{3}\) = 0
3(x² + y²) – 29x – 19y + 56 = 0

ప్రశ్న 2.
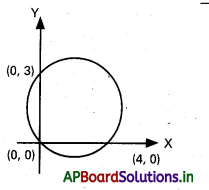
i) (0, 0) గుండా పోతూX, Y అక్షాలపై వరసగా 4, 3 అంతర ఖండాలు చేసే వృత్త సమీకరణాన్ని కనుక్కోండి.
సాధన:
x² + y² + 2gx + 2fy + c = 0
(0,0), (4, 0) మరియు (0, 3) ల గుండా వృత్తం పోతుంది.
0 + 0 + 2g(0) + 2f(0) + c = 0
c = 0 …………………………… (i)

16 + 0 + 8g + 2f. 0 + c = 0
c = 0 కనుక g = -2
ఇదే విధంగా 0 + 9 + 2g. 0 + 6f + c = 0
f = – \(\frac{3}{2}\) అయిన c = 0
కావలసిన వృత్త సమీకరణము
x² + y² – 4x – 3y = 0
(2), (1) అంతర ఖండాలు రుణాత్మకంగా తీసుకొంటే వృత్తం (0, 0) (−4, 0), (0, -3) బిందువు ల గుండా పోతుంది. ఇదే విధంగా ఈ వృత్త సమీకరణం
x² + y² + 4x + 3y = 0 అని చూపవచ్చును.

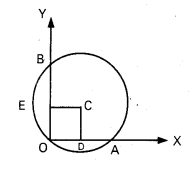
ii) (0, 0) గుండా పోతూX, Y అక్షాలపై వరసగా 6,4 అంతర ఖండాలు చేసే వృత్త సమీకరణం కనుక్కోండి.
సాధన:
OA = 6 యూనిట్లు
OB = 4 యూనిట్లు
OD = 3 యూనిట్లు. OE = 2 యూనిట్లు
∴ కేంద్రం నిరూపకాలు (3, 2)
వ్యాసార్ధము OC = \(\sqrt{(0+3)^2+(0-2)^2}\)
= \(\sqrt{13}\)
(h, k) కేంద్రం, r వ్యాసార్ధం గల వృత్త సమీకరణము
(x – h)² + (y – k)² = r²
∴ కావలసిన వృత్త సమీకరణము
(x – 3)² + (y – 2)² = 13
x² + y² – 6x – 4y = 0
అంతర ఖండాలు రుణాత్మకంగా తీసుకొంటే వృత్తం (0, 0) (-6, 0), (0, -4) బిందువు ల గుండా పోతుంది.
ఇదే విధంగా ఈ వృత్త సమీకరణము
x² + y² + 6x + 4y = 0 అని చూపవచ్చును

ప్రశ్న 3.
కింది బిందువులు చక్రీయాలు అని చూపి వాటి గుండా పోయే వృత్త సమీకరణాలను కనుక్కోండి.
i) (1, 1), (6, 0), (-2, 2), (-2, -8)
సాధన:
కావలసిన వృత్త సమీకరణము
x² + y² + 2gx + 2fy + c = 0 ……………… (i)
ఈ వృత్తము A (1, 1) గుండా పోతూ
1 + 1 + 2g + 2f + c = 0
⇒ 2g + 2f + c = 2 ……………… (ii)
ఈ వృత్తము B (- 6, 0) గుండా పోతూ
36 + 0 – 12g + 0 + c = 0
– 12g + c = -36 ……………………. (iii)
ఈ వృత్తము C (-2, 2) గుండా పోతూ
4 + 4 – 4g + 4f + c = 0
– 4g + 4f + c = -8 ………………….. (iv)
(iii) – (iv) చేయగా -8g – 4f = 0
⇒ 2g + f = 7
(i) – (ii) చేయగా 14g + 2f = 34
7g + f = 17 ……………….. (v)
(iv) నుండి (v) సాధించగా g = 2, f=3
g = 2, f = 3 అని (i) లో ప్రతిక్షేపించగా
4 + 6 + c =-2
c = 12
వృత్త సమీకరణము x² + y² + 4x + 6y – 12 = 0
(- 2, – 8) ను సమీకరణములో ప్రతిక్షేపించగా
4 + 64 – 8 – 48 – 12 = 68 – 68 = 0
(− 2, – 8) బిందువుపై సమీకరణాన్ని తృప్తిపరుస్తాయి.
∴ A, B, C, D లు చక్రీయాలు.
వృత్త సమీకరణము
x² + y² + 4x + 6y – 12 = 0

ii) (1, 2); (3,4); (5, 6); (19, 8)
సాధన:
వృత్త సమీకరణము x² + y² + 2gx + 2fy + c = 0
1 + 4 + 2g + 4 + c = 0 ………………. (i)
9 + 16 + 6g – 8f + c = 0 ………………. (ii)
25 + 36 + 10g – 12f + c = 0 …………………. (iii)
(ii) – (i) చేయగా
20 + 4g – 12f = 0
5 + g – 3f = 0 ……………….. (iv)
(iii) – (ii) చేయగా
36 + 4g – 4f = 0
(లేదా)
9 + g – f = 0 …………………. (v)
(iv) మరియు (v) సాధించగా.
f = -2, g = -11, c = 25
వృత్త సమీకరణము
x² + y² – 22x – 4y + 25 = 0 …………………… (vi)
(19, 8) ను (vi) లో ప్రతిక్షేపించగా
(19)² + 8² – 22 × 19 – 4 × 8 + 25 = 0
(19, 8) బిందువు వృత్తం మీద ఉంది కనుక దత్త బిందువులు చక్రీయాలు.

iii) (1,6); (5, 2); (7, 0); (-1,-4)
సాధన:
వృత్త సమీకరణము x² + y² + 2gx + 2fy + c = 0
1 + 36 + 2g – 12f + c = 0 …………………… (i)
25 + 4 + 10g + 4f + c = 0 …………………….. (ii)
49 + 14g + c = 0 ………………. (iii)
(ii) – (i) చేయగా
-8 + 8g + 16f = 0
(లేదా)
2f + g – 1 = 0 ………………. (iv)
(iii) – (ii) చేయగా
20 + 4g – 4f = 0 ……………….. (v)
(లేదా)
5 + g – f = 0
(iv) నుండి (v) సాధించగా
f = 2, g = -3, c = -7
వృత్త సమీకరణము
x² + y² – 6x + 4y – 7 = 0 ………….. (vi)
(- 1, – 4) బిందువు (vi) ను తృప్తి పరుస్తుంది.
∴ దత్త బిందువులు చక్రీయాలు

iv) (9, 1), (7, 9), (-2, 12), (6, 10)
సాధన:
వృత్త సమీకరణము
x² + y² + 2gx + 2fy + c = 0
ఈ వృత్తం A(9, 1), B(7, 9), C(- 2,2) ల గుండా పోతుంది.
81 + 1 + 18g + 2f + c = 0 …………………. (i)
49 + 81 + 14g + 18f + c = 0 …………………. (ii)
4 + 144 – 4g + 24f + c = 0 …………………. (iii)
(ii) – (i) చేయగా – 4g + 16f + 48 = 0
4g – 16f = 48
g – 4f = 12 ……………. (iv)
(ii) – (iii) 18g – 6f – 18 = 0
+ 18g – 6f = 18 ………………. (v)
+ 36g – 12f = 36 …………….. (v) × 2
3g – 12f = 36 ……………. (iv) × 3
తీసివేయగా 33g = 0 ⇒ g = 0
(iv) లో ప్రతిక్షేపించగా – 4f = 12
f = \(\frac{12}{-4}\) = -3
g, f ల విలువలు (i) లో ప్రతిక్షేపించగా
18 – 0 + 2(-3) + c + 82 = 0
c = 6 – 82 = -76
కావలసిన వృత్త సమీకరణము
x² + y² – 6y – 76 = 0
x² + y² – 6y – 76 = 6² + 10² – 6(10) – 76
= 36 + 199 – 60 – 76
= 136 – 136 = 0
D(6, 10) A, B, C ల గుండా పోయే వృత్తం మీద ఉండి.
∴ A, B, C మరియు D లు చక్రీయాలు.
వృత్త సమీకరణము x² + y² – 6y – 76 = 0

ప్రశ్న 4.
(2, 0), (0, 1), (4, 5) (0, c) బిందువులు చక్రీయాలు అయితే C విలువ ఎంత ?
సాధన:
x² + y² + 2gx + 2fy + c₁ = 0
(2, 0), (0, 1) (4, 5) బిందువులను తృప్తిపరుస్తుంది కనుక
4 + 0 + 4g + c₁ = 0 …………….. (i)
0 + 1 + 2g. 0 + 2f + c₁= 0 ……………. (ii)
16 + 25 + 8g + 10f + c₁ = 0 ………………. (iii)
(ii) – (i) చేయగా
-3 – 4g + 2f = 0
4g – 2f = -3 …………….. (iv)
(ii) – (iii) చేయగా
-40 – 8g – 8f = 0 (or)
g + f = -5 ……………… (v)
(iv), (v) లు సాధించగా
g = –\(\frac{13}{6}\), f = –\(\frac{17}{6}\)
(i) లో g, f ల విలువలు ప్రతిక్షేపించగా
4 + 4 \(\left(-\frac{13}{6}\right)\) + c₁ = 0
c₁ = \(\frac{14}{3}\)
వృత్త సమీకరణము x² + y² – \(\frac{13}{3}\)x – \(\frac{17}{3}\)y + \(\frac{14}{3}\) = 0
వృత్తం (0, c) గుండా పోతుంది.
c² – \(\frac{17}{c}\)c + \(\frac{14}{3}\) = 0
3c² – 17c + 14 = 0
⇒ (3c – 14) (c – 1) = 0
(లేదా)
c = 1 లేదా \(\frac{14}{3}\)

ప్రశ్న 5.
క్రింద ఇచ్చిన రేఖలతో ఏర్పడే త్రిభుజాల పరివృత్త సమీకరణాలను కనుక్కోండి.
i) 2x + y = 4; x + y = 6; x + 2y = 5
సాధన:
AB: 2x + y = 4
AB : 2x + y = 4
BC : x + y = 6
AC : x + 2y = 5
B : (-2, 8)
A : (1,2)
AC : x + 2y = 5
BC : x + y = 6
C : (7, -1)

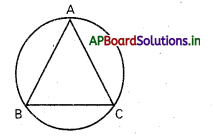
వృత్త సమీకరణము x² + y² + 2gx + 2fy + c = 0
A, B, C ల గుండా పోతూ
∴ 4 + 64 – 4g + 16f + c = 0 …………… (i)
1 + 4 + 2g + 4f + c = 0 ………………… (ii)
49 + 1 + 14g – 2f + c = 0 …………………. (iii)
(i) – (ii) చేయగా
(iii) – (ii) చేయగా
21 – 2g + 4f = 0 ……………. (iv)
15 + 4g – 2f = 0 …………………. (v)
(iv), (v) లు సాధించగా f = –\(\frac{19}{2}\)
g = – \(\frac{17}{2}\) ; c = 50
g. f ల విలువలు (i) లో ప్రతిక్షేపించగా
∴ కావలసిన వృత్త సమీకరణము
x² + y² – 17x – 19y + 50 = 0

ii) x + 3y – 1 = 0; x + y + 1 = 0; 2x + 3y + 4 = 0
సాధన:
AB : x + 3y – 1 = 0
AB : x + 3y – 1 = 0
AC : x + y + 1 = 0
AC : x + y + 1 = 0.
A : (1, -2)
B : (-5, 2)
BC : 2x + 3y + 4 = 0
BC : 2x + 3y + 4 = 0
C (-2, 1)

వృత్త సమీకరణము x² + y² + 2gx + 2fy + c = 0
A, B, C లు వృత్తం మీది బిందువులు.
∴ 1 + 4 + 2g – 4f + c = 0 …………… (i)
25 + 4 – 10g + 4f + c = 0 ……………….. (ii)
4 + 1 – 4g + 2f + c = 0 ………………. (iii)
(i) – (iii) చేయగా
6g – 6f = 0 (or) g = f ……………… (iv)
(i) – (ii) చేయగా
24 – 12g + 8f = 0 ……………. (v)
(iv), (v) లు సాధించగా
g = 6, f = 6, c =7
కావలసిన వృత్త సమీకరణము
x² + y² + 12x + 12y + 7 = 0

iii) 5x – 3y + 4 = 0; 2x + 3y – 5 = 0; x + y = 0.
సాధన:
AB : 5x – 3y + 4 = 0.
AC : 2x + 3y – 5 = 0
BC : x + y = 0
A : \(\left(\frac{1}{7}, \frac{11}{7}\right)\)
B : \(\left(-\frac{1}{2}, \frac{1}{2}\right)\)
C : (-5, 5)
AB : 5x – 3y + 4 = 0
BC : x + y = 0
వృత్త సమీకరణము
x² + y² + 2gx + 2fy + c = 0
A, B, C లు వృత్తం మీది బిందువులు


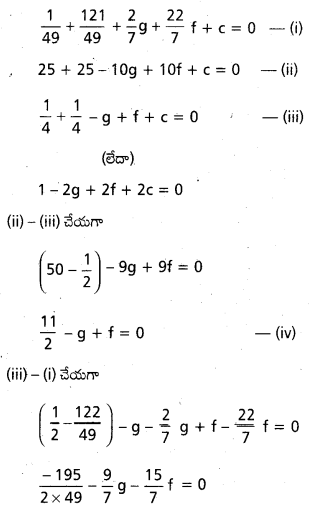
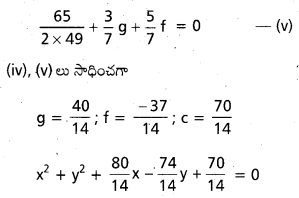
వృత్త సమీకరణము
7(x² + y²) + 40x – 37y + 35 = 0

iv) x – y – 2 = 0;
2x – 3y + 4 = 0;
3x – y + 6 = 0
సాధన:
AB: x – y – 2 =0
B: (10, 8)
A : (-4, -6)
BC : 2x – 3y + 4 = 0
AC : 3x – y + 6 = 0
C : (-2, 0)
వృత్త సమీకరణము
x² + y² + 2gx + 2fy + c = 0
A, B, C లు వృత్తం మీది బిందువులు
100 + 64 + 20g + 16f + c = 0 …………….. (i)
16 + 36 – 8g – 12f + c = 0 …………….. (ii)
4 – 4g + c = 0 …………….. (iii)
పై సమీకరణాలను సాధించగా
g = – 12, f = 8, c = 52
కావలసిన వృత్త సమీకరణము.
x² + y² – 24x + 16y – 52 = 0

ప్రశ్న 6.
x cos α + y sin α = a, x sin α – y cos α = b (α పరామితి) సరళరేఖల ఖండన బిందువు పథం ఒక వృత్తమని చూపండి.
సాధన:
దత్త రేఖల సమీకరణాలు
x cos α + y sin α= a
x sin α – y cos α = b
p (x, y) ఖండన బిందువు
x₁ cos α + y₁ sin α = a ……………… (1).
x₁ sin α – y₁ cos α = b ………………… (2)
(1), (2) లను వర్గీకరించి కూడగా
(x₁ cos α + y₁ sin α)² + (x₁ sin α – y₁ cos α)² = a² + b²
x₁² cos² α + y₁² sin² α + 2x₁y₁ cos α sin α + x₁² sin² α + y₁² cost α – 2x₁y₁ cos α sin α = a² + b²
x₁² (cos² a + sin² α) + y₁²(sin² α + cos² α) = a² + b²
x₁² + y₁² = a² + b²
p(x₁, y₁) బిందుపథం ఒక వృత్తం. దాని సమీకరణము
x² + y² = a² + b²

ప్రశ్న 7.
ఇచ్చిన రెండు బిందువుల నుండి చర బిందువుకి ఉన్న దూరాల నిష్పత్తి స్థిర సంఖ్య (1) అయితే దీని బిందుపథం ఒక వృత్తమని చూపండి.
సాధన:
P(x, y,) బిందు పథం మీది బిందువు
A (a, 0), B (-a, 0) లు దత్త బిందువులు
దత్తాంశం \(\frac{\mathrm{PA}}{\mathrm{PB}}\) = k,(≠ ± 1)