Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Chapter 4 దీర్ఘవృత్తం Exercise 4(b) will help students to clear their doubts quickly.
AP Inter 2nd Year Maths 2B Solutions Chapter 4 దీర్ఘవృత్తం Exercise 4(b)
అభ్యాసం – 4(బి)
I.
ప్రశ్న 1.
x2 + 8y2 = 33 దీర్ఘవృత్తంపై (-1, 2) బిందువు వద్ద స్పర్శరేఖ, అభిలంబ రేఖల సమీకరణాలు కనుక్కోండి.
సాధన:
స్పర్శరేఖ సమీకరణము
\(\frac{xx_1}{a^2}+\frac{y y_1}{b^2}\) = 1
x(-1) + 8y(2) = 33
⇒ – x + 16y = 33
⇒ x – 16y + 33 = 0
అభిలంబరేఖ సమీకరణము
16x + y + k = 0
ఇది P(-1, 2) గుండా పోతుంది.
-16 + 2 + k = 0 ⇒ k = 14
అభిలంబరేఖ సమీకరణము
16x + y + 14 = 0
ప్రశ్న 2.
x2 + 2y2 – 4x + 12y + 14 = 0 దీర్ఘవృత్తంపై (2, – 1) బిందువు వద్ద స్పర్శరేఖ, అభిలంబ రేఖల సమీకరణాలు కనుక్కోండి.
సాధన:
స్పర్శరేఖ సమీకరణం
xx1 + 2yy1 – 2(x + x1) + 6(y + y1) + 14 = 0
⇒ 2x – 2y – 2(x + 2) + 6(y – 1) + 14 = 0
⇒ 4y + 4 = 0
దీర్ఘవృత్త స్పర్శరేఖ సమీకరణము y = – 1
స్పర్శరేఖ వాలు ‘0’
అభిలంబ రేఖా సమీకరణము
y + 1 = \(\frac{-1}{0}\)(x – 2)
x = 2
![]()
ప్రశ్న 3.
9x2 + 16y2 = 144 దీర్ఘవృత్తానికి, నిరూపక అక్షాలపై సమాన అంతరఖండాలు చేసే స్పర్శరేఖ సమీకరణం కనుక్కోండి.
సాధన:
దీర్ఘవృత్తం సమీకరణము
9x2 + 16y2 = 144
⇒ \(\frac{x^2}{16}+\frac{y^2}{9}\) = 1
స్పర్శరేఖా సమీకరణము
\(\frac{x}{a}\) cos θ + \(\frac{y}{b}\) sin θ = 1
స్పర్శరేఖ వాలు = –\(\frac{b \cos \theta}{a \sin \theta}\) = -1
cot θ = \(\frac{a}{b}=\frac{4}{3}\)
cos θ = ± \(\frac{4}{5}\), sin θ = ± \(\frac{3}{5}\)

ప్రశ్న 4.
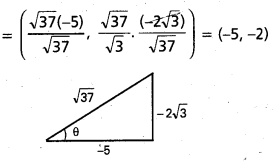
దీర్ఘవృత్తం x2 + 3y2 = 37 పై ఏ బిందువుల వద్ద గీసిన అభిలంబ రేఖలు 6x – 5y = 2 కు సమాంతరంగా ఉంటాయో. ఆ బిందువు నిరూపకాలు కనుక్కోండి.
సౌధన:
దీర్ఘవృత్తం సమీకరణము x2 + 3y2 = 37

సందర్భం (i) : P నిరూపకాలు, θ మొదటి పాదంలో కోణం
(a cos θ, b sin θ)
\(\left(\sqrt{37}, \frac{5}{\sqrt{37}}, \frac{\sqrt{37}}{\sqrt{3}}, \frac{2 \sqrt{3}}{\sqrt{37}}\right)\) = (5, 2)
సందర్భం (ii) : P నిరూపకాలు, θ మూడవ పాదంలో కోణం (a cos θ, b sin θ)
![]()
ప్రశ్న 5.
x2 + 3y2 = 3 దీర్ఘవృత్తానికి 4x + y + k = 0 స్పర్శరేఖ అయితే k విలువ కనుక్కోండి. [A.P. Mar. ’16]
సాధన:
దీర్ఘవృత్తం సమీకరణము x2 + 3y2 = 3
⇒ \(\frac{x^2}{3}+\frac{y^2}{1}\) = 1
a2 = 3, b2 = 1, రేఖా సమీకరణము 4x + y + k = 0
y = -4x – k
m = -4, c = -k
స్పర్శరేఖ నియమము c2 = a2m2 + b2
(-k)2 = 3(-4)2 + 1
k2 = 48 + 1 = 49
k = ± 7
ప్రశ్న 6.
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 దీర్ఘవృత్తానికి x cos α + y sin α = p స్పర్శరేఖ కావడానికి నియమం కనుక్కోండి.
సాధన:
దీర్ఘవృత్తం సమీకరణం
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 ………….. (1)
సరళరేఖ సమీకరణము x cos α + y sin α = p
y sin α = x cos α + p
y = -x. \(\frac{\cos \alpha}{\sin \alpha}+\frac{p}{\sin \alpha}\)
∴ m = –\(\frac{\cos \alpha}{\sin \alpha}\), c = \(\frac{\mathrm{p}}{\sin \alpha}\)
స్పర్శరేఖా నియమము c2 = a2m2 + b2
\(\frac{\mathrm{p}^2}{\sin ^2 \alpha}=a^2 \cdot \frac{\cos ^2 \alpha}{\sin ^2 \alpha}+b^2\)
లేదా p2 = a2 cos2 α + b2 sin2 α
![]()
II.
ప్రశ్న 1.
2x2 + 3y2 = 11 దీర్ఘవృత్తానికి y నిరూపకం 1 గా గల బిందువుల వద్ద స్పర్శరేఖ, అఖిలంబ రేఖల సమీకరణాలు కనుక్కోండి. [T.S. Mar. ’16]
సాధన:
దీర్ఘవృత్తం సమీకరణం 2x2 + 3y2 = 11
y = 1 అని ఇవ్వబడింది.
2x2 + 3 = 11 ⇒ 2x2 = 8
x2 = 4
x = ± 2
స్పర్శ బిందువులు P(2, 1) మరియు Q(-2, 1)
సందర్భం (i) : P(2, 1)
స్పర్శరేఖా సమీకరణము 2x . 2 + 3y. 1 = 11
4x + 3y = 11
అభిలంబ రేఖ, స్పర్శరేఖకు లంబంగా ఉంది.
అభిలంబ రేఖా సమీకరణము
3x – 4y = k
అభిలంబ రేఖ P(2, 1) గుండా పోతుంది
6 – 4 = k ⇒ k = 2
P వద్ద అభిలంబ రేఖా సమీకరణము 3x – 4y = 2
సందర్భం (ii) : Q(-2, 1)
Q వద్ద స్పర్శరేఖా సమీకరణము
2x(-2) + 3y.1 = 11
– 4x + 3y = 11
4x – 3y + 11 = 0
అభిలంబ రేఖా సమీకరణము
3x + 4y = k గా తీసుకొనవచ్చును
అభిలంబ రేఖ (-2, 1) గుండా పోతుంది.
– 6 + 4 = k ⇒ k = – 2
Q వద్ద అభిలంబ రేఖా సమీకరణము 3x + 4y = -2
లేదా 3x + 4y + 2 = 0
![]()
ప్రశ్న 2.
x2 + 2y2 = 3 దీర్ఘవృత్తానికి బిందువు (1, 2) నుంచి గీసిన స్పర్శరేఖల సమీకరణాలు, వాటి మధ్య కోణం కనుక్కోండి.
సాధన:
దీర్ఘవృత్తం సమీకరణము x2 + 2y2 = 3
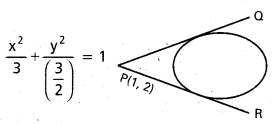
a2 = 3, b2 = \(\frac{3}{2}\)
స్పర్శరేఖ వాలు m. ఇది P(1, 2) గుండా పోతుంది.
స్పర్శరేఖా సమీకరణము y – 2 = m (x – 1)
y = mx + (2-m)
= mx – m
స్పర్శరేఖా నియమము c2 = a2m2 + b2
(2 – m)2 = 3(m2) + \(\frac{3}{2}\)
4 + m2 – 4m = 3m2 + \(\frac{3}{2}\)
2m2 + 4m – \(\frac{5}{2}\) = 0
4m2 + 8m – 5 = 0
(2m – 1) (2m + 5) = 0
m = \(\frac{1}{2}\) లేదా – \(\frac{5}{2}\)
సందర్భం (i) : m = \(\frac{1}{2}\)
స్పర్శరేఖా సమీకరణము y = \(\frac{1}{2}\)x + 2 – \(\frac{1}{2}\)
= \(\frac{x}{2}\) + \(\frac{3}{2}\)
2y = x + 3
x – 2y + 3 = 0
సందర్భం (ii) : m = – \(\frac{5}{2}\)
స్పర్శరేఖా సమీకరణము y = – \(\frac{5}{2}\)x + (2 + \(\frac{5}{2}\))
= –\(\frac{5}{2}\)x + \(\frac{9}{2}\)
2y = -5x + 9
లేదా 5x + 2y – 9 = 0
స్పర్శరేఖల మధ్య కోణము θ అయితే
tan θ = \(\left|\frac{m_1-m_2}{1+m_1 m_2}\right|\)
= \(\left|\frac{\frac{1}{2}+\frac{5}{2}}{1+\left(\frac{1}{2}\right)\left(-\frac{5}{2}\right)}\right|=\left|\frac{3}{1-\frac{5}{4}}\right|\)
= |- 12 | = 12
θ = tan-1 (12)
![]()
ప్రశ్న 3.
2x2 + y2 = 8 దీరప్పత్తానికి కింది నియమాలు పాటించే స్పర్శరేఖల సమీకరణాలు కనుక్కోండి.
i) x – 2y – 4 = 0 సరళరేఖకు సమాంతరంగా [Mar. ’06; May ’05]
సాధన:
స్పర్శరేఖ వాలు = \(\frac{1}{2}\)

స్పర్శరేఖల సమీకరణము 2y – x ± 6 = 0
లేదా x – 2 y ± 6 = 0
ii) x+y+ 2 = 0 సరళరేఖకు లంబంగా
సాధన:
స్పర్శరేఖ దత్తరేఖకు లంబంగా ఉంది కనుక దాని వాలు ‘1’
స్పర్శరేఖా సమీకరణము y = mx ± \(\sqrt{a^2 m^2+b^2}\)
y = x ± \(\sqrt{4+8}\) స్పర్శరేఖా సమీకరణము
y = x ± 2\(\sqrt{3}\)
x – y ± 2\(\sqrt{3}\)
iii) X – అక్షంతో \(\frac{\pi}{4}\) కోణం చేసే
సాధన:
స్పర్శరేఖా సమీకరణము y = x ± 2\(\sqrt{3}\)
![]()
ప్రశ్న 4.
దీర్ఘవృత్తం 3x2 + 13y2 = 78 తో ఏక కేంద్రీయ వృత్త వ్యాసార్ధం 4 అయితే ఉమ్మడి స్పర్శరేఖ దీర్ఘాక్షంతో \(\frac{\pi}{4}\) కోణం చేస్తుందని చూపండి.
సాధన:
దీర్ఘవృత్తం సమీకరణం 3x2 + 13y2 = 78
\(\frac{x^2}{26}+\frac{y^2}{6}\) = 1 …………… (1)
దీర్ఘవృత్త కేంద్రం (0, 0)
∴ వృత్త సమీకరణము x2 + y2 = 16 ……………… (2)
P(θ) వద్ద వృత్తానికి స్పర్శరేఖా సమీకరణము
x cos θ + y sin θ = 16 ………………. (3)
y = \(\frac{-\cos \theta}{\sin \theta} \cdot x+\frac{16}{\sin \theta}\)
(3) రేఖ దీర్ఘవృత్తానికి స్పర్శరేఖ.
∴ c2 = a2m2 + b2
\(\frac{256}{\sin ^2 \theta}\) = 26. \(\frac{\cos ^2 \theta}{\sin ^2 \theta}\) + 6
16 = 26 cos2θ + 6 sin2θ
= 26 cos2θ + 6(1 – cos2θ)
= 26 cos2θ + 6 – 6 cos2 θ
20 cos2 θ = 10
cos2 θ = \(\frac{10}{20}\) = \(\frac{1}{2}\)
cos θ = ± \(\frac{1}{\sqrt{2}}\)
θ = \(\frac{\pi}{4}\)
![]()
III.
ప్రశ్న 1.
దీర్ఘవృత్త కేంద్రం నుంచి ఏదైనా స్పర్శరేఖపైకి గీసిన లంబ పాదాలు వక్రం (x2 + y2)2 = a2x2 + b2y2 పై ఉంటాయని చూపండి.
సాధన:
దీర్ఘవృత్త సమీకరణము \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1
P(θ) వద్ద స్పర్శరేఖా సమీకరణము
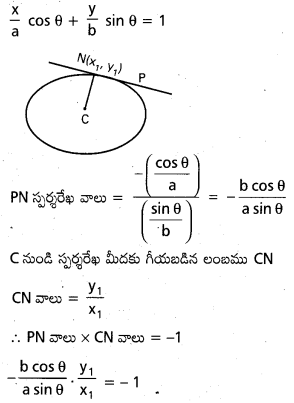
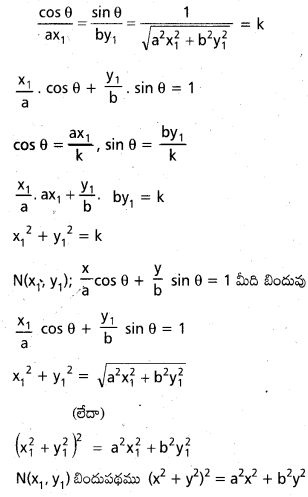
![]()
ప్రశ్న 2.
దీర్ఘవృత్తపు ఏదైనా స్పర్శరేఖ పైకి నాభుల నుంచి గీసిన లంబపాదాల బిందు పథం అనుబంధ (సహాయక) వృత్తం అని చూపండి.
సాధన.
(± ae, 0) నుండి స్పర్శరేఖ మీద గీయబడిన లంబం సమీకరణము
y = – \(\frac{1}{m}\) (x ± ae)
my = -(x ± ae)
my + x = ± ae ……………… (1)
(1), (2) లను వర్గీకరించి కలుపగా
(y – mx)2 + (my + x)2 = a2m2 + b2 + a2e2
y2 + m2x2 – 2mxy + m2y2 + x2 + 2mxy
= a2m2 + a2 – a2e2 + a2e2
(x2 + y2) (1 + m2) = a2(1 + m2).
⇒ x2 + y2 = a2
బిందుపథము సహాయక వృత్తం.
ఇది దీర్ఘవృత్తానికి ఏక కేంద్రీయము.
![]()
ప్రశ్న 3.
x2 + 4y2 = 4 దీర్ఘవృత్తంపై P(θ) వద్ద స్పర్శరేఖ, అభిలంబ రేఖలు వరుసగా దీర్ఘాక్షాన్ని Q, R ల మధ్య ఖండిస్తున్నాయి. 0 < 0 < \(\frac{\pi}{2}\), QR = 2 అయితే θ = cos-1\(\left(\frac{2}{3}\right)\) అని చూపండి.
సాధన:
దీర్ఘవృత్తం సమీకరణం x2 + 4y2 = 4
\(\frac{x^2}{4}+\frac{y^2}{1}\) = 1
P(θ) వద్ద స్పర్శరేఖ సమీకరణము
\(\frac{x}{2}\) cos θ + \(\frac{y}{1}\) sin θ = 1
X – అక్షం సమీకరణం y = 0
\(\frac{x}{2}\) cos θ = 1 ⇒ x = \(\frac{2}{\cos \theta}\)
Q నిరూపకాలు \(\left(\frac{2}{\cos \theta}, \theta\right)\)
P(θ) వద్ద అభిలంబ రేఖా సమీకరణం
\(\frac{a x}{\cos \theta}-\frac{\text { by }}{\sin \theta}\) = a2 – b2
\(\frac{2 x}{\cos \theta}-\frac{y}{\sin \theta}\) = 3
y = 0 ప్రతిక్షేపిస్తే

– 3 cos2 θ + 4 = 4 cos θ
3 cos2 θ + 4 cos θ – 4 = 0
(3 cos θ – 2) (cos θ + 2) = 0
3 cos θ – 2 = 0 లేదా cos θ + 2 = 0
cos θ = \(\frac{2}{3}\) లేదా cos θ = -2
cos θ విలువ ఎల్లప్పుడూ -1, 1 ల మధ్య ఉంటుంది.
∴ cos θ = \(\frac{2}{3}\)
i.e., θ = cos -1\(\left(\frac{2}{3}\right)\)