AP Inter 2nd Year Physics Important Questions Chapter 11 Electromagnetic Waves

Students get through AP Inter 2nd Year Physics Important Questions 11th Lesson Electromagnetic Waves which are most likely to be asked in the exam.

AP Inter 2nd Year Physics Important Questions 11th Lesson Electromagnetic Waves

Very Short Answer Questions

Question 1.
Give anyone use of infrared rays. [T.S. Mar. 17; A.P. Mar. 16]
Answer:

1. Infrared radiation plays an important role in maintaining the Earth warm.
2. Infrared lamps are used in physical therapy.
3. Infrared detectors are used on Earth Satellites.
4. These are used in taking photographs during conditions of fog, smoke, etc.

Question 2.
How are infrared rays produced? How they can be detected?
Answer:
Vibrations of atoms and molecules can produce infrared rays. These waves can be detected by Thermopile, Bolometer, and IR photographic film.

Question 3.
How are radio waves produced? How can they detect it?
Answer:
Radio waves can be produced by rapid acceleration and deceleration of electrons in aerials (conductors). These can be detected by receivers of aerials.

Question 4.
If the wave length of E.M radiation is doubled, what happens to the energy of photon ? [IPE 2016 (TS)]
Answer:
If the wave length of electromagnetic radiation is doubled, then energy will be halved because energy is inversely proportional to.wavelength of electromagnetic waves.
E = hυ = hc/λ ⇒ E ∝ 1/λ (∵ hc is a constant)

Question 5.
What is the principle of production of electromagnetic waves ?
Answer:
If the charge is accelerated both the magnetic field and electric field will change with Space and time, then electromagnetic waves are produced.

Question 6.
What is the ratio of speed of infrared rays and ultraviolet rays in vaccum ?
Answer:
The ratio of speed of infrared rays and ultraviolet rays in vacuum is 1 : 1.
All electromagnetic waves travel with same speed 3 × 10⁸ m /s in vaccum.

Question 7.
What is the relation between the amplitudes of the electric and magnetic fields in free space for an electromagnetic wave ?
Answer:
E₀ = CB₀
Where E₀ = Amplitude of electric field.
B₀ = Amplitude of magnetic field.
C = velocity of light.

Question 8.
What are the applications of microwaves ? [A.P. Mar. 17; T.S. Mar. 15]
Answer:

1. Microwaves are used in Radars.
2. Microwaves are used for cooking purposes.
3. A radar using microwave can help in detecting the speed of automobile while in motion.

Question 9.
Microwaves are used in Radars, why ? [Mar. 14]
Answer:
As microwaves are of smaller wavelengths, hence they can be transmitted as a beam signal in a particular direction. Microwaves do not bend around the comers of any obstacle coming in their path.

Question 10.
Give two uses of infrared rays.
Answer:

1. Infrared rays are used for producing dehydrated fruits.
2. They are used in the secret writings on the ancient walls.
3. They are used in green houses to keep the plants warm.

Question 11.
How are microwaves produced ? How can they detected ? [A.P. Mar. 16; IPE 15]
Answer:
Microwaves can be produced using Klystron valve or Magnetrons.
Microwaves can be detected using point contact diodes.

Question 12.
The charging current for a capacitor is 0.6 A. What is the displacement current across its plates ?
Answer:
i = charging current for a capacitor = 0.6 A
i = i_d = ε₀ = \(\frac{\mathrm{d} \phi_{\mathrm{B}}}{\mathrm{dt}}\)
∴ i = i_d = 0.6 A
∴ Displacement current (i_d) = 0.6 A.

Question 13.
What physical quantity is the same for X-rays of wavelength 10^-10m, red light of wavelength 6800 Å and radiowaves of wavelength 500in ?
Answer:
The speed in vaccum is same for all the given wavelengths, which is 3 × 10⁸ m/s.

Question 14.
A radio can tune into any station in the 7.5 MHz to 12MHz band. What is the corresponding wavelength band ?
Answer:
λ₁ = \(\frac{3 \times 10^8}{7.5 \times 10^6}\) = 40 m
λ₂ = \(\frac{3 \times 10^8}{12 \times 10^6}\) = 25 m
Thus wavelength band is 40m to 25m.

Question 15.
The amplitude of the magnetic field part of a harmonic electromagnetic wave in vaccum is B₀ = 510 nT. What is the amplitude of the electric field part of the wave ?
Answer:
Here, B₀ = 510nT = 510 × 10^-9T
E₀ = CB₀ = 3 × 10⁸ × 510 × 10^-9 = 153 NC^-1.

Question 16.
Define displacement current
Answer:
Displacement current (I_d) is equal to ε₀ times to the rate of change of electric flux. Displacement current is not the current produced due to charge carried. But it is due to varying electric flux. It is the current in the sense that it produces a magnetic field.
I_d = ε₀ \(\frac{\mathrm{d} \phi_{\varepsilon}}{\mathrm{dt}}\)

Short Answer Questions

Question 1.
State six characteristics of electromagnetic waves.
Answer:
Characteristics of electromagnetic waves :

1. Electromagnetic waves are produced by accelerated charges.
2. Electromagnetic waves are transverse in nature.
3. Electromagnetic waves donot require material medium for their propagation.
4. Electromagnetic waves obey principle of superposition of waves.
5. Velocity of E.M waves in vaccum depends on permittivity and permeability of free space.
6. Electromagnetic waves carry energy and momentum.
7. Electromagnetic waves exert pressure when they strike a surface.

Question 2.
What is Greenhouse effect and its contribution towards the surface temperature of earth ?
Answer:
Green house effect: Temperature of the earth increases due to the radiation emitted by
the earth is trapped by atmospheric gases like CO₂, CH₄, N₂, chlorofluoro carbons etc., is called green house effect.

1. Radiation from the sun enters the atmosphere and heat the objects on the earth. These heated objects emit infrared rays.
2. These rays are reflected back to Earth’s surface and trapped in the Earth’s atmosphere. Due to this temperature of the earth increases.
3. The layers of carbon dioxide (CO₂) and low lying clouds prevent infrared rays to escape Earth’s atmosphere.
4. Since day-by-day the amount of carbondioxide in the atmosphere increases, more • infrared rays are entrapped in the atmosphere.
5. Hence the temperature of the Earth’s surface increases day by day.

Problems

Question 1.
A plane electromagnetic wave travels in vaccum along z-direction. What can you say about the directions of its electric and magnetic field vectors ? If the frequency of the wave is 30 MHz. What is its wavelength ?
Answer:
Electric and magnetic fields \(\overline{\mathrm{E}}\) and \(\overline{\mathrm{B}}\) of an electromagnetic wave must be perpendicular to the propagation of electromagnetic wave. Hence they lie in X – Y plane mutually perpendicular to each other.
Frequency of wave, v = 30MHz = 30 × 10⁶Hz.; Velocity of light, C = 3 × 10⁸m/s
Wavelength of the wave, λ = \(\frac{C}{V}=\frac{3 \times 10^8}{30 \times 10^6}\) = 10m

Question 2.
A charged particle oscillates about its mean equilibrium position with a frequency of 109 Hz. What is the frequency of the electromagnetic waves produced by the oscillator ?
Answer:
According to Maxwell, a charged particle oscillating with a frequency produces electro-magnetic waves of same frequency. Hence frequency of EM waves produced is, 10⁹Hz.

Textual Examples

Question 1.
A parallel plate capacitor with circular plates of radius 1 m has a capacitance of 1 nF. At t = 0, It is connected for charging in series with a resistor R = 1 M Q across a 2V battery (fig)- Calculate the magnetic field at a point P halfway between the centre and the periphery of the plates, after t = 10^-3 s. (The charge on the capacitor at time τ is q (t) = CV [1 – exp (-t/τ)], where the time constant τ is equal to CR.).
Solution:
The time constant of the CR circuit is τ = CR = 10^-3s. Then, we have
q(t) = CV [1 – exp (-t/τ) ]
= 2 × 10^-9 [1 – exp (-t /10^-3)
The electric field in between the plates at time t is
E = \(\frac{q(t)}{\varepsilon_0 A}=\frac{q}{\pi \varepsilon_0}\); A = π (1)² m² = area of the plates.

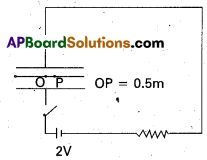
Consider now a circular loop of radius (1/2)m parallel to the plates passing through R The magnetic field B at all points on the loop is along the loop arid of the same value.
The flux Φ_E through this loop is
The flux Φ_E = E × area of the loop
= E × π × (\(\frac{1}{2}\))² = \(\frac{\pi \mathrm{E}}{4}=\frac{\mathrm{q}}{4 \varepsilon_0}\)
The displacement current
i_d = e₀ \(\frac{\mathrm{d} \phi_{\mathrm{E}}}{\mathrm{dt}}\) = \(\frac{1}{4} \frac{\mathrm{dq}}{\mathrm{dt}}\) = 0.5 × 10^-6 exp (-1)
at t = 10^-3s. Now, applying Ampere-Maxwell law to the loop, we get
B × 2π × (\(\frac{1}{2}\)) = m₀.(i_c + i_d) = m₀(0 + i_d) = 0.5 × 10^-6 m₀ exp(-1)
or, B = 0.74 × 10^-13 T.

Question 2.
A plane electromagnetic wave of frequency 25 MHz travels in free space along the x – direction. At a particular point in space and time, E = \(6.3 \hat{\mathbf{j}}\) V/m. What is B at the point ?
Solution:
Using Eq. B₀ = [E₀/c] the magnitude of B is
B = \(\frac{\mathrm{E}}{\mathrm{c}}\)
= \(\frac{6.3 \mathrm{~V} / \mathrm{m}}{3 \times 10^8 \mathrm{~m} / \mathrm{s}}\) = 2.1 × 10^-8 T
To find the direction, we note that E is along y-direction and the wave propagates along x- axis. Therefore, B should be in a direction perpendicular to both x- and y-axes. Using vector algebra, E × B should be along x-direction. Since, \((+\hat{\mathrm{j}})\) × \((+\hat{\mathrm{k}})\) = i, B is along the z-direction. Thus. B = 2.1 × 10^-8 \(\hat{\mathrm{k}}\) T

Question 3.
The magnetic field in a plane electromagnetic wave is given by
B_y = 2 × 10^-7 sin (0.5 × 10³ × + 1.5 × 10¹¹ t)T.
a) What is the wavelength and frequency of the wave ?
b) Write an expression for the electric field.
Solution:
a) Comparing the given equation with
B_y = B₀ sin \(\left[2 \pi\left(\frac{\mathrm{x}}{\lambda}+\frac{\mathrm{t}}{\mathrm{T}}\right)\right]\)
We get, λ = \(\frac{2 \pi}{0.5 \times 10^3}\) m = 1.26 cm,
and \(\frac{1}{\mathrm{~T}}\) = v = (1.5 × 10¹¹)/2π = 23.9 GHz

b) E₀ = B₀C = 2 × 10^-7 T × 3 × 10⁸ m/s = 6 × 10¹ V/m
The electric field component is perpendicular to the direction of propagation and the di-rection of magnetic field. Therefore, the electric field component along the z-axis is obtained as E_z = 60 sin (0.5 × 10³x + 1.5 × 10¹¹t) V/m.

Question 4.
Light with an energy flux of 18 W/cm² falls on a non reflecting surface at normal incidence. If the surface has an area of 20 cm² find the average force exerted on the surface during a 30 minute time span.
Solution:
The total energy falling on the surface is
U = (18 W/cm²) × (20 cm²) × (30 × 60)
= 6.48 × 10⁵ J
Therefore, the total momentum delivered (for complete absorption) is
P = \(\frac{\mathrm{U}}{\mathrm{C}}=\frac{6.48 \times 10^5 \mathrm{I}}{3 \times 10^8 \mathrm{m} / \mathrm{s}}\) = 2.16 × 10^-3 kg m/s
The average force exerted on the surface is
F = \(\frac{\mathrm{p}}{\mathrm{t}}=\frac{2.16 \times 10^{-3}}{0.18 \times 10^4}\) = 1.2 × 10^-6 N

Question 5.
Calculate the electric and magnetic fields produced by the radiation coming from a 100 W bulb at a distance of 3m. Assume that the efficiency of the bulb is 2.5% and it is a point source.
Solution:
The bulb, as a point source, radiates light in all directions uniformly. At a distance of 3m, the surface area of the surrounding sphere is A = 4 πr² = 4π (3)² = 113m²
The intensity at this distance is
I = \(\frac{\text { Power }}{\text { Area }}=\frac{100 \mathrm{~W} \times 2.5 \%}{113 \mathrm{~m}^2}\) = 0.022 W.m²
Half of this intensity is provided by the electric field and half by the magnetic field.
\(\frac{1}{2} I=\frac{1}{2}\left(\varepsilon_0 \mathrm{E}_{\mathrm{rms}}^2 \mathrm{C}\right)\)
= \(\frac{1}{2}\) (0.022 W/m²)
E_rms = \(\sqrt{\frac{0.022}{\left(8.85 \times 10^{-12}\right)\left(3 \times 10^8\right)}}\) V/m = 2.9 V/m
The value of E found above is the root mean square value of the electric field. Since the electric field in a light beam is sinusoidal, the peak electric field, E₀ is
E₀ = \(\sqrt{2}\)E_rms = \(\sqrt{2}\) × 2.9 V/m
= 4.07 V/m
Thus, you see that the electric field strength of the light that you use for reading is fairly large. Compare it with electric field strength of TV or FM waves, which is of the order of a few microvolts per metre.
Now, let us calculate the strength of the magnetic field. It is
B_rms = \(\frac{E_{\mathrm{rms}}}{\mathrm{C}}=\frac{2.9 \mathrm{Vm}^{-1}}{3 \times 10^8 \mathrm{~ms}^{-1}}\) = 9.6 × 10^-9 T.
Again, since tbs field in the light beam is sinusoidal, the peak magnetic field is B₀ = \(\sqrt{2}\) B_rms = 1.4 × 10^-8 T. Note that although the energy in the magnetic field is equal to the energy in the electric field, the magnetic field strength is evidently very weak.