Students get through AP Inter 2nd Year Physics Important Questions 4th Lesson Electric Charges and Fields which are most likely to be asked in the exam.
AP Inter 2nd Year Physics Important Questions 4th Lesson Electric Charges and Fields
Very Short Answer Questions
Question 1.
What is meant by the statement ‘charge is quantized’? [IPE 2015 (TS)]
Answer:
The minimum charge that can be transferred from one body to the other is equal to the charge of the electron (e = 1.602 × 10-19C). A charge always exists an integral multiple of charge of electron (q = ne). Therefore charge is said to be quantized.
Question 2.
Repulsion is the sure test of charging than attraction. Why ?
Answer:
A charged body may attract a neutral body and also an opposite charged body. But it always repels like a charged body. Hence repulsion is the sure test of electrification.
![]()
Question 3.
How many electrons constitute 1 C of charge ?
Answer:
n = \(\frac{\mathrm{q}}{\mathrm{e}}=\frac{1}{1.6 \times 10^{-19}}\) = 6.25 × 1018 electrons
Question 4.
What happens to the weight of a body when it is charged positively ?
Answer:
When a body is positively charged it must loose some electrons. Hence, weight of the body will decrease.
Question 5.
What happens to the force between two charges if the distance between them is [Board Model Paper]
a) halved
b) doubled ?
Answer:
From Coulombs law, F ∝ \(\frac{1}{\mathrm{~d}^2}\). So
a) When distance is reduced to half, force increases by four times.
[∵ F2 = \(\frac{F_1 d_1^2}{\left(\frac{d_1}{2}\right)^2}\) = 4 F1]
b) When distance is doubled to half, force increases by four times.
[∵ F2 = \(\frac{F_1 d^2}{\left|2 d_1\right|^2}\) = \(\frac{1}{4}\) F1]
Question 6.
The electric lines of force do not intersect. Why ?
Answer:
They do not intersect because if they intersect, at the point of intersection, intensity of electric field must act in two different directions, which is impossible.
![]()
Question 7.
Consider two charges + q and -q placed at B and C of an equilateral triangle ABC. For this system, the total charge is zero. But the electric field (intensity) at A which is equidistant from B and C is not zero. Why ?
Answer:
Charges are scalars, but the electrical intensities are vectors and add vectorially.
Question 8.
Electrostatic field lines of force do not form closed loops. If they form closed loops then the work done in moving a charge along a closed path will not be zero. From the above two statements can you guess the nature of electrostatic force ?
Answer:
It is conservative force.
Question 9.
State Gauss’s law in electrostatics. [IPE 2015 (TS)]
Answer:
Gauss’s law: It states that “the total electric flux through any closed surface is equal to \(\frac{1}{\varepsilon_0}\) times net charge enclosed by the surface”.
\(\oint \overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{ds}}=\frac{\mathrm{q}}{\varepsilon_0}\)
Question 10.
When is the electric flux negative and when is it positive ?
Answer:
Electric flux Φ = \(\overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{A}}\). If angle between \(\overrightarrow{\mathrm{E}}\) and \(\overrightarrow{\mathrm{A}}\) is 180°, then flux will have a -ve’ sign. We consider the flux flowing out of the surface as positive and flux entering into the surface as negative.
Question 11.
Write the expression for electric intensity due to an infinite long charged wire at a distance radial distance r from the wire.
Answer:
The electric intensity due to an infinitely long charged wire E = \(\frac{\lambda}{2 \pi \varepsilon_0 r}\) perpendicular to the conductor.
Where λ = Uniform linear charge density
r = Distance of the point from the conductor.
![]()
Question 12.
Write the expression for electric intensity due to an infinite plane sheet of charge.
Answer:
The electric intensity due to an infinite plane sheet of charge is E = \(\frac{\sigma}{2 \varepsilon_0}\).
Question 13.
Write the expression for electric intensity due to a charged conducting spherical shell at points outside and inside the shell.
Answer:
a) Intensity of electric field at any point inside a spherical shell is zero.
b) Intensity of electric field at any point- outside a uniformly charged spherical shell is
E = \(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{q}{r^2}\)
Question 14.
A proton and an α-particle are released in a uniform electric field. Find the ratio of (a) forces experienced by them (b) accelerations gained by each.
Answer:
a) As F = Eq, F ∝ q, ⇒ \(\frac{F_p}{F_\alpha}=\frac{Q_p}{Q_\alpha}=\frac{1}{2}\)
∴ \(\frac{F_p}{F_\alpha}=\frac{1}{2}\)
b) As a = \(\frac{E Q}{m}\) ⇒ a ∝ \(\frac{Q}{m}\) ⇒ \(\frac{a_p}{a_\alpha}=\frac{e_p}{Q_\alpha} \times \frac{m_\alpha}{m_p}=\frac{1}{2} \times \frac{4}{1}=\frac{2}{1}\)
∴ \(\frac{a_p}{a_\alpha}=\frac{2}{1}\)
Question 15.
The electric field in a region is given by \(\bar{E}=a \bar{i}+b \bar{j}\). Here a and b are constants. Find the net flux passing through a square area of side L parallel to y-z plane.
Answer:
Electric field, \(\bar{E}=a \bar{i}+b \bar{j}\)
Flux passing through square area, Φ = \(\overline{\mathrm{E}} \cdot \overline{\mathrm{A}}=(\mathrm{a} \overline{\mathrm{i}}+\mathrm{b} \overline{\mathrm{i}}) \cdot\left(\mathrm{L}^2 \overline{\mathrm{i}}\right)\) = aL2 Wb
![]()
Question 16.
A hollow sphere of radius ‘r’ has a unifrom charge density ‘σ’. It is kept in a cube of edge 3r such that the center of the cube coincides with the center of the shell. Calculate the electric flux that comes out of a face of the cube.
Answer:
Charge on the hallow sphere, q = σ × 4πr2.
The flux through a single face of the cube, Φ1 = \(\frac{f}{6}=\frac{1}{6} \cdot \frac{Q}{\varepsilon_0}=\frac{\sigma \times 4 \pi \mathrm{r}^2}{6 \varepsilon_0}=\frac{2 \pi \mathrm{r}^2 \sigma}{3 \varepsilon_0}\)
Question 17.
Consider a uniform electric field ![]() . What is the flux of this field through a square of 10 cm on a side whose plane is parallel to the YZ plane ?
. What is the flux of this field through a square of 10 cm on a side whose plane is parallel to the YZ plane ?
Answer:
Given, ![]() (field is along positive x-axis)
(field is along positive x-axis)
Surface area of square, S = (10 × 10-2)(10 × 10-2) = 10-2m2.
When plane of the square is parallel to yz-plane its area vector points towards 4-ve x-axis.
So θ = 0°.
∴ Flux through square, Φ = EScosθ = 3 × 103 × 10-2 × cos0° => <(> = 30 NC-1m2.
Short Answer Questions
Question 1.
State and explain Coulomb’s inverse square law in electricity. [T.S. Mar. 17; Mar. 14]
Answer:
Coulomb’s law – Statement: Force between two charges is proportional to the product of the charges and inversely proportional to the square of the distance between them. The force acts along the straight line joining the two charges.
Explanation : Let us consider two charges q1 and q2 be separated by a distance r.

Then F ∝ q1q2 and F ∝ \(\frac{1}{\mathrm{r}^2}\) or F ∝ \(\frac{\mathrm{q}_1 \mathrm{q}_2}{\mathrm{r}^2}\)
∴ F = \(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{\mathrm{q}_1 \mathrm{q}_2}{\mathrm{r}^2}\) where \(\frac{1}{4 \pi \varepsilon_0}\) = 9 × 109 Nm2C-2.
In vector form, in free space \(\overrightarrow{\mathrm{F}}=\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}_1 \mathrm{q}_2}{\mathrm{r}^2} \hat{\mathrm{r}}\). Here \(\hat{\mathrm{r}}\) is a unit vector.
ε0 is called permittivity of free space.
ε0 = 8.85 × 10-12 C2/N-m2 or Farad/meter.
In a medium, Fm = \(\frac{1}{4 \pi \varepsilon} \frac{\mathrm{q}_1 \mathrm{q}_2}{\mathrm{r}^2}=\frac{1}{4 \pi \varepsilon_0 \varepsilon_{\mathrm{r}}} \times \frac{\mathrm{q}_1 \mathrm{q}_2}{\mathrm{r}^2}\) [∵ ε = ε0εr]
Where ε is called permittivity of the medium.
![]()
Question 2.
Define intensity of electric field at a point. Derive an expression for the intensity due to a point charge. [A.P. Mar. 16]
Answer:
Intensity of electric field (E) : Intensity of electric field at any point in an electric field is defined as the force experienced by a unit positive charge placed at that point.
Expression :
- Intensity of electric field is a vector. It’s direction is along the direction of motion of positive charge.
- Consider point charge q. Electric field will exist around that charge. Consider any point P in that electric field at a distance r from the given charge. A test charge q0 is placed at P.
- Force acting on q0 due to q is F = \(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{\mathrm{qq}_0}{\mathrm{r}^2}\)
- Intensity of electric field at that point is equal to the force experienced by a test charge q0.
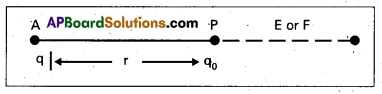
Intensity of electric field, E = \(\frac{\mathrm{F}}{\mathrm{q}_0}\)
E = \(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{\mathrm{q}}{\mathrm{r}^2}\)N/C or V/m
Question 3.
Derive the equation for the couple acting on a electric dipole in a uniform electric field.
Answer:
- A pair of opposite charges separated by a small distance is called dipole.
- Consider the charge of dipole are -q and +q coulomb and the distance between them is 2a.
- Then the electric dipole moment P is given by P = q × 2a = 2aq. It is a vector. It’s direction is from -q to +q along the axis of dipole.
- It is placed in a uniform electric field E, making an angle θ with, field direction as shown in fig.
- Due to electric field force on +q is F = +.qE and force on -q is F = -qE.
- These two equal and opposite charges constitute torque or moment of couple.
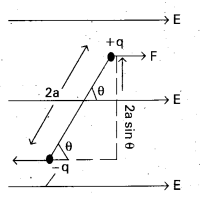
i.e., torque, τ = ⊥r distance × magnitude of one of force
∴ τ = (2a sin θ)qE = 2aqE sin θ = PE sin θ - In vector form, \(\vec{\tau}=\overrightarrow{\mathrm{P}} \times \overrightarrow{\mathrm{E}}\)
![]()
Question 4.
Derive an expression for the intensity of the electric field at a point on the axial line of an electric dipole. [A.P. Mar. 17; T.S. Mar. 16]
Answer:
Electric field at a point on the axis of a dipole :
- Consider an electric dipole consisting of two charges -q and + q separated by a distance ‘2a’ with centre ‘O’.
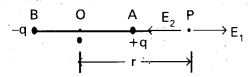
- We shall calculate electric field E at point P on the axial line of dipole, and at a distance OP = r.
- Let E1 and E2 be the intensities of electric field at P due to charges + q and -q respectively.

Question 5.
Derive an expression for the intensity of the electric field at a point on the equatorial plane of an electric dipole. [A.P. Mar. 15]
Answer:
Electric field intensity on equatorial line of electric dipole :
- Consider an electric dipole consisting of two charges-q and +q separated by a distance ‘2a’ with centre at ’O’.
- We shall calculate electric field E at P on equatorial line of dipole and at a distance OP = r.
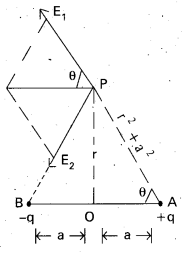
- Let E1 and E2 be the electric fields at P due to charges +q and -q respectively.
- The ⊥r components (E1 sin θ and E2 sin θ) cancel each other because they are equal and opposite. The I lel components (E1 cos θ and E2 cos θ) are in the same direction and hence add up.
- The resultant field intensity at point P is given by E = E1 cos θ + E2 cos θ
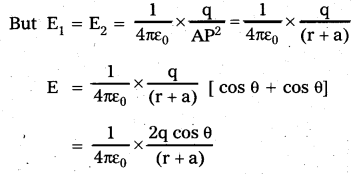
- From figure, cos θ = \(\frac{a}{\left(r^2+a^2\right)^{1 / 2}}\)
∴ E = \(\frac{1}{4 \pi \varepsilon_0} \times \frac{2 \mathrm{aq}}{\left(\mathrm{r}^2+\mathrm{a}^2\right)^{3 / 2}}\) - If r >> a, then a2 can be neglected in comparison to r2. Then E
E = \(\frac{\mathrm{P}}{4 \pi \varepsilon_0} \times \frac{1}{\mathrm{r}^3}\)
In vector form E = \(\overrightarrow{\mathrm{E}}=\frac{\overrightarrow{\mathrm{P}}}{4 \pi \varepsilon_0 \mathrm{r}^3}\)
![]()
Question 6.
State Gauss’s law in electrostatics and explain its importance. [T.S. Mar. 15]
Answer:
Gauss’s law : The total electric flux through any closed surface is equal to \(\frac{1}{\varepsilon_0}\) times the net charge enclosed by the surface.
Total electric flux, Φ = \(\oint_{\mathrm{s}} \overrightarrow{\mathrm{E}} \cdot \mathrm{d} \overrightarrow{\mathrm{s}}=\frac{\mathrm{q}}{\varepsilon_0}\)
Here q is the total charge enclosed by the surface ‘S’, \(\oint\) represents surface integral of the closed surface.
Importance :
- Gauss’s law is very useful in calculating the electric field in case of problems where it is possible to construct a closed surface. Such surface is called Gaussian surface.
- Gauss’s law is true for any closed surface, no matter what its shape or size.
- Symmetric considerations in many problems make the application of Gauss’s law much easier.
Long Answer Questions
Question 1.
State Gauss’s law in electrostatics. Applying Gauss’s law derive the expression for electric intensity due to an infinite plane sheet of charge.
Answer:
Gauss’s law : The total electric flux through any closed surface is equal to \(\frac{1}{\varepsilon_0}\) times the net charge enclosed by the surface. i.e., Φ = \(\oint_{\mathrm{s}} \overrightarrow{\mathrm{E}} \cdot \mathrm{d} \overrightarrow{\mathrm{s}}=\frac{\mathrm{q}}{\varepsilon_0}\)
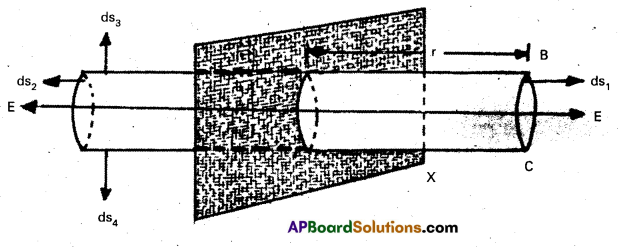
Expression for E due to an infinite plane sheet of charge:
- Consider an infinite plane sheet of charge Let the charge distribution is uniform on this plane.
- Uniform charge density on this surface σ = \(\frac{\mathrm{dq}}{\mathrm{dS}}\) where dq is the charge over an infinite small area ds.
- Construct a horizontal cylindrical Gaussian surface ABÇD perpendicular to the plane with length 2r.
- The flat surfaces BC and AD are parallel to the plane sheet and are at equal distance from the plane.
- Let area of these surfaces are dS1 and dS2. They are parallel to \(\overrightarrow{\mathrm{E}}\). So flux through
these two surfaces is \(\oint_{\mathrm{S}} \overrightarrow{\mathrm{E}} \cdot \mathrm{d} \overrightarrow{\mathrm{S}}=\int\) Eds = E(S + S) = 2ES ……………….. (1) - Consider cylindrical surface of AB and CD. Let their areas are say dS3 and dS4. These surfaces are ⊥r to electric intensity \(\overrightarrow{\mathrm{E}}\).
- So angle between \(\overrightarrow{\mathrm{E}}\) and d\(\overrightarrow{S_3}\) or dS4 is 90°. Total flux through these surfaces is zero.
Since \(\oint_S\) E.dS = 0. - From Gauss’s law total flux, Φ = \(\oint \overrightarrow{\mathrm{E}} \cdot \mathrm{d} \overrightarrow{\mathrm{S}}\) = 2ES = \(\frac{\mathrm{q}}{\varepsilon_0}\)
∴ 2ES = \(\frac{\sigma S}{\varepsilon_0}\) [∵Q = σ × S] - Therefore intensity of electric field due to an infinite plane sheet of charge E = \(\frac{\sigma}{2 \varepsilon_0}\).
Textual Examples
Question 1.
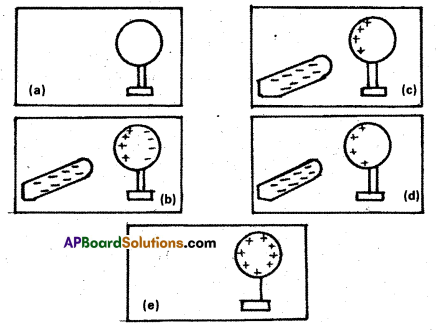
How can you charge a metal sphere positively without touching it ?
Solution:
Figure (a) shows an uncharged metallic sphere on an insulating metal stand. Bring a negatively charged rod close to the metallic sphere, as shown in Fig. (b). As the rod is brought close to the sphere, the free electrons in the sphere move away due to repulsion and start piling up at the farther end. The near end becomes positively charged due to deficit of electrons. This process of charge distribution stops when the net force on the free electrons inside the metal is zero. Connect the sphere to the ground by a conducting wire. The electrons will flow to the ground while the positive charges at the near end will remain held there due to the attractive force of the negative charges on the rod, as shown in Fig. (c). Disconnect the sphere from the ground. The positive charge continues to be held at the near end [Fig. 4.5 (d)]. Remove the electrified rod. The positive charge will spread uniformly over the sphere as shown in Fig. (e).
![]()
Question 2.
If 109 electrons move out of a body to another body every second, how much time is required to get a total charge of 1 C on the other body? .
Solution:
In one second electrons move out of the body. Therefore the charge given out in one second is 1.6 × 10-19 × 109C = 1.6 × 10-10 C. The time required o accumulate a charge of 1 C can then be estimated to be 1 C ÷ (1.6 × 10-10 C/s) = 6.25 × 109 s = 6.25 × 109 ÷ (365 × 24 × 3600) years = 198 years. Thus to collect a charge of one coulomb, from a body from which 109 electrons move, out every second, we will need approximately 200 years. One coulomb is, therefore, a very large unit for many practical purposes.
It is, however, also important to know what is roughly the number of electrons contained in a piece of one cubic centimetre of a material. A cubic piece of copper of side 1 cm contains about 2.5 × 1024 electrons.
Question 3.
How much positive and negative charge is there in a cup of.water ?
Solution:
Let us assume that the mass of one cup of water is 250 g. The molecular mass of. water is 18g. Thus, one mole (= 6.02 × 1023 molecules) of water is 18 g. Therefore the number of molecules in one cup of water is (250/18) × 6.02 × 1023.
Each molecule of water contains two hydrogen atoms and one oxygen atom, i.e., 10 electrons and 10 protons. Hence the total positive and total negative charge has the same magnitude. It is equal to (250/18) × 6.02 × 1023 × 10 × 1.6 × 10-19 C = 1.34 × 107C.
![]()
Question 4.
Coulomb’s law for electrostatic force between two point charges and Newton’s law for gravitational force between two stationary point masses, both have inverse-square depen-dence on the distance between the charges/masses, (a) Compare the strength of these forces by determining the ratio of their magnitudes (i) for an electron and a protron and (ii) for two protons (b) Estimate the accelerations of electron and proton due to the electrical force of their mutual attraction when they are 1 Å (= 10-10 m) apart ?
(mp = 1.67 × 10-27 kg, m3 = 9.11 × 10-31 kg).
Solution:
a) i) The electric force between an electron and a proton at a distance r apart is :
Fe = –\(\frac{\mathrm{m}_{\mathrm{p}} \mathrm{m}_{\mathrm{e}}}{\mathrm{r}^2}\)
Where the negative sign indicates that the force is attractive. The corresponding gravitational force (always attractive) is :
FG = -G\(\frac{\mathrm{m}_{\mathrm{p}} \mathrm{m}_{\mathrm{e}}}{\mathrm{r}^2}\)
Where mp and me are the masses of a proton and an electron respectively.
\(\left|\frac{\mathrm{F}_{\mathrm{e}}}{\mathrm{F}_{\mathrm{G}}}\right|=\frac{\mathrm{e}^2}{4 \pi \varepsilon_0 \mathrm{Gm}_{\mathrm{p}} \mathrm{m}_{\mathrm{e}}}\) = 2.4 × 1039
ii) On similar lines, the ratio of the magnitudes of electric force to the gravitational force between two protons at a distance r apart is :
\(\left|\frac{\mathrm{F}_{\mathrm{e}}}{\mathrm{F}_{\mathrm{G}}}\right|=\frac{\mathrm{e}^2}{4 \pi \varepsilon_0 \mathrm{G} \mathrm{m}_{\mathrm{p}} \mathrm{m}_{\mathrm{e}}}\) = 1.3 × 1036
However, it may be mentioned here that the signs of the two forces are different. For two protons, the gravitational force is attractive in nature and the Coulomb force is repulsive. The actual values of these forces between two protons inside a nucleus (distance between two protons
is ~ 10-15m inside a nucleus) are Fe ~ 230 N whereas FG ~ 1.9 × 10-34 N.
The (dimensionless) ratio of the two forces shows that electrical forces are enormously stronger than the gravitational forces.
b) The electric force F exerted by a proton on an electron is same in magnitude to the force exerted by an electron on a proton; however the masses of an electron and a proton are different. Thus, the magnitude of force is
|F| = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{e}^2}{\mathrm{r}^2}\) = 8.987 × 109 Nm2/C2 × (1.6 × 10-19C)2 / (10-10 m)2
= 2.3 × 10-8N
Using Newton’s second law of motion, F = ma, the acceleration that an electron will undergo is a = 2.3 × 10-8 N/9.11 × 10-31 kg = 2.5 × 1022 m/s2
Comparing this with the value of acceleration due to gravity, we can conclude that the effect of gravitational field is negligible on the motion of electron and it undergoes very large accelerations under the action of Coulomb force due to a proton.
The value for acceleration of the proton is
a = 2.3 × 10-8 N/1.67 × 10-27 kg = 1.4 × 109 m/s2.
Question 5.
A charged metallic sphere A is suspended by a nylon thread. Another charged metallic sphere B held by an insulating handle is brought close to A such that the distance between their centres is 10 cm, as shown in Fig. (a). The resulting repulsion of A is noted (for example, by shining a beam of light and measuring the deflection of its shadow on a screen). Spheres A and B are touched by uncharged spheres C and D respectively, as shown in Fig. (b). C and D are then removed and B is brought closer to A to a distance of 5.0 cm between their centres, as shown in Fig. (c). What is the expected repulsion of A on the basis of Coulomb’s law ? Spheres A and C and spheres B and D have identical sizes. Ignore the size of A and B in comparison to the separation between their centres.
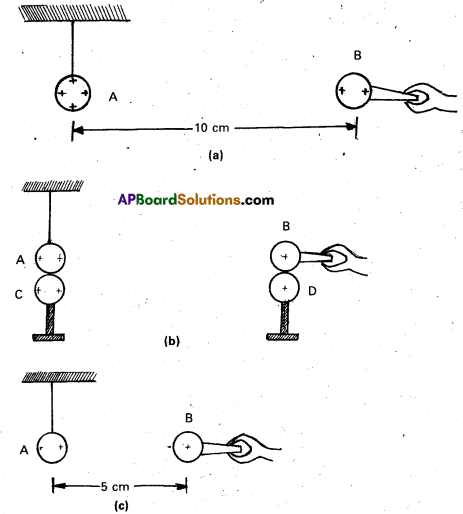
Solution:
Let the original charge on sphere A be q and that on B be q’. At a distance r between their centres, the magnitude of the electrostatic force on each is given by
F = \(\frac{1}{4 \pi \varepsilon_0} \frac{\left(\mathrm{qq}^{\prime}\right)}{\mathrm{r}^2}\)
Neglecting the sizes of spheres A and B in comparison to r. When an identical but uncharged sphere C touches A, the charges redistribute on A and C and by symmetry, each sphere carries a charge q/2. Similarly, after D touches B, the redistributed charge on each is q’/2. Now, if the separation between A and B is halved, the magnitude of the electrostatic force on each is
F’ = \(\frac{1}{4 \pi \varepsilon_0} \frac{(\mathrm{q} / 2)\left(\mathrm{q}^{\prime} / 2\right)}{(\mathrm{r} / 2)^2}=\frac{1}{4 \pi \varepsilon_0} \frac{\left(\mathrm{qq}^{\prime}\right)}{\mathrm{r}^2}\) = F
Thus the electrostatic force on A, due to B, remains unaltered.
![]()
Question 6.
Consider three charges q1, q2, q3 each equal to q at the vertices of an equilateral triangle of side l. What is the force on a charge Q (with the same sign as q) placed at the centroid of the triangle, as shown in Fig. ?
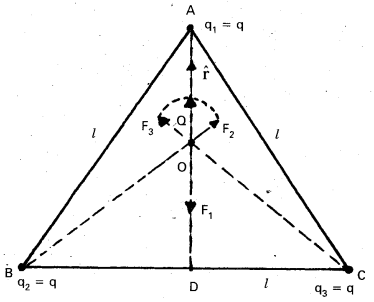
Solution:
In the given equilateral triangle ABC of sides of length l, if we draw a perpendicular AD to the side BC,
AD = AC cos 30° = \(\left(\frac{\sqrt{3}}{2}\right) l\) and the distance AO of the centroid O from A is
(2/3) AD = \(\left(\frac{1}{\sqrt{3}}\right) l\).
By symmetry AO = BO = CO.
Thus,
Force F1 on Q due to charge q at A = \(\frac{3}{4 \pi \varepsilon_0} \frac{\mathrm{Qq}}{l^2}\) along AO
Force F2 on Q due to charge q at B = \(\frac{3}{4 \pi \varepsilon_0} \frac{\mathrm{Qq}}{l^2}\) along BO
Force F3 on Q due to charge q at C = \(\frac{3}{4 \pi \varepsilon_0} \frac{\mathrm{Qq}}{l^2}\) along CO
The resultant of forces F2 and F3 is \(\frac{3}{4 \pi \varepsilon_0} \frac{\mathrm{Qq}}{l^2}\) along OA, by the parallelogram law. Therefore, the total force on Q = \(\frac{3}{4 \pi \varepsilon_0} \frac{\mathrm{Qq}}{l^2}(\hat{\mathrm{r}}-\hat{\mathrm{r}})\) = 0, where \(\hat{\mathrm{r}}\) is the unit vector along OA.
It is clear also by symmetry that the three forces will sum to zero. Suppose that the resultant force was non-zero but in some direction. Consider what would happen if the system was rotated through 60° about O.
Question 7.
Consider the charges q, q and -q placed at the vertices of an equilateral triangle, as shown in Fig. What is the force on each charge ?
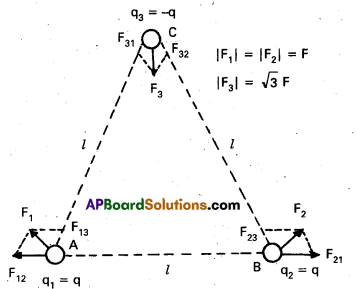
Solution:
The forces acting on charge q at A due to charges q at B and -q at C are F12 along BA and F13 along AC respectively, as shown in Fig. By the parallelogram law, the total force F1 on the charge q at A is given by
F1 = F \(\hat{\mathrm{r}}_1\) where \(\hat{\mathrm{r}}_1\) is a unit vector along BC.
The force of attraction or repulsion for each pair of charges has the same magnitude
F = \(\frac{\mathrm{q}^2}{4 \pi \varepsilon_0 l^2}\)
The total force F2 on charge q at B is thus F2 = F \(\hat{\mathrm{r}}_2\), where \(\hat{\mathrm{r}}_2\) is a unit vector along AC.
Similarly the total force on charge -q at C is F3 = \(\sqrt{3} \mathrm{~F} \hat{\mathrm{n}}\), where \(\hat{\mathrm{n}}\) is the unit vector along the direction bisecting the ∠BCA.
It is interesting to see that the sum of the forces on the three charges is zero, i.e.,
F1 + F2 + F3 = 0
The result is not at all surprising. It follows straight from the fact that Coulomb’s law is consistent with Newton’s third law. The proof is left to you as an exercise.
![]()
Question 8.
An electron falls through a distance of 1.5 cm in a uniform electric field of magnitude 2.0 × 104 N C-1 (Fig. a). The direction of the field is reversed keeping its magnitude unchanged and a proton falls through the same distance (Fig. b) Compute the time of fall in each case. Contrast the situation with that of ‘free fall under gravity’.
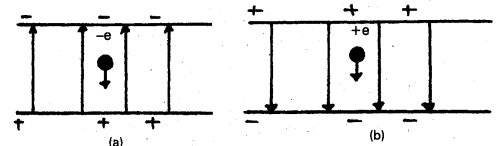
Solution:
In Fig. (a) the field is upward, so the negatively charged electron experiences a downward force of magnitude eE where E is the magnitude f the electric field. The acceleration of the electron is ae = eE/me.
Where me is the mass of the electron.
Starting from rest, the time required by the electron to fall through a distance h is given by
te = \(\sqrt{\frac{2 \mathrm{~h}}{\mathrm{a}_{\mathrm{e}}}}=\sqrt{\frac{2 \mathrm{hm_{ \textrm {e } }}}{\mathrm{eE}}}\)
For e = 1.6 × 10-19C, me = 9.11 × 10-31 kg.
E = 2.0 × 104 NC-1, h 1.5 × 10-2 m.
te = 2.9 × 10-9 s
In Fig. (b), the field is downward and the positively charged proton experiences a downward force of magnitude eE. The acceleration of the proton is
ap = eE/mp
Where mp is the mass of the proton ; mp = 1.67 × 10-27 kg. The time of fall for the proton is
tp = \(\sqrt{\frac{2 \mathrm{~h}}{\mathrm{a}_{\mathrm{p}}}}=\sqrt{\frac{2 h \mathrm{~m}_{\mathrm{p}}}{\mathrm{eE}}}\) = 1.3 × 10-7 s
Thus, the heavier particle (proton) takes a greater time to fall through the same distance. This is in basic contrast to the situation of, free fall under gravity’ where the time of fall is independent of the mass of the body. Note that in this example we have ignored the acceleration due to gravity in calculating the time of fall. To see if this is justified, let us calculate the acceleration of the proton in the given electric field
ap = \(\frac{\mathrm{eE}}{\mathrm{m}_{\mathrm{p}}}=\frac{\left(1.6 \times 10^{-19} \mathrm{C}\right) \times\left(2.0 \times 10^4 \mathrm{NC}^{-1}\right)}{1.67 \times 10^{-27} \mathrm{~kg}}\)
= 1.9 × 1012 ms-2
Which is enormous compared to the value of g (9.8 ms-2), the acceleration due to gravity. The acceleration of the electron is even greater. Thus, the effect of acceleration due to gravity can be ignored in this example.
Question 9.
Two point charges q1 and q2, of magnitude +10-8 C and -10-8 C, respectively, are placed 0.1 m apart. Calculate the electric fields at points A, B and C shown in Fig.
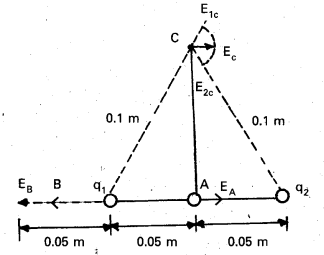
Solution:
The electric field vector E1A at A due to the positive charge qx points towards the right and has a magnitude
E1A = \(\frac{\left(9 \times 10^9 \mathrm{Nm}^2 \mathrm{C}^{-2}\right) \times\left(10^{-8} \mathrm{C}\right)}{(0.05 \mathrm{~m})^2}\) = 3.6 × 104 NC-1
The electric field vector E2A at A due to the negative charge q2 points towards the right and has the same magnitude. Hence the magnitude of the total electric field EA at A is
EA = E1A + E2A = 7.2 × 104 NC-1
EA is directed toward the right.
The electric field vector E1B at B due to the positive charge q1 points towards the left and has a magnitude.
E1B = \(\frac{\left(9 \times 10^9 \mathrm{Nm}^2 \mathrm{C}^{-2}\right) \times\left(10^{-8} \mathrm{C}\right)}{(0.05 \mathrm{~m})^2}\) = 3.6 × 104 NC-1
The electric field vector E2B at B due to the negative charge q2 points towards the right and has a magnitude.
E2B = \(\frac{\left(9 \times 10^9 \mathrm{Nm}^2 \mathrm{C}^{-2}\right) \times\left(10^{-8} \mathrm{C}\right)}{(0.15 \mathrm{~m})^2}\) = 4 × 104 NC-1
The magnitude of the total electric field at B is EB = E1B – E2B = 3.2 × 104 NC-1
EB is directed towards the left.
The magnitude of each electric field vector at point C, due to charge q1 and q2 is
E1C = E2C = \(\frac{\left(9 \times 10^9 \mathrm{Nm}^2 \mathrm{C}^{-2}\right) \times\left(10^{-8} \mathrm{C}\right)}{(0.10 \mathrm{~m})^2}\) = 9 × 103 NC-1
The directions in which these two vectors point are indicated in Fig. The resultant of these two vectors is
EC = E1 cos \(\frac{\pi}{3}\) + E2 cos \(\frac{\pi}{3}\) = 9 × 103 NC-1
EC points towards the right.
![]()
Question 10.
Two charges 10 μC are placed 5.0 mm apart. Determine the electric field at (a) a point P on the axis of the dipole 15 cm away from its centre O on the side of the positive charge, as shown in Fig. (a) and (b) a point Q, 15 cm away from O on a line passing through O and normal to the axis of the dipole, as shown in Fig. (b).
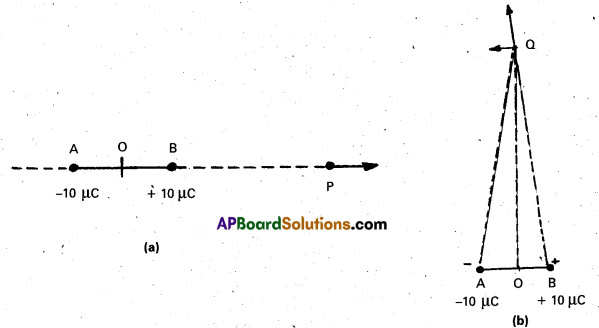
Solution:
a) Field at P due to charge +10 μC
= \(\frac{10^{-5} \mathrm{C}}{4 \pi\left(8.854 \times 10^{-12} \mathrm{C}^2 \mathrm{~N}^{-1} \mathrm{~m}^{-2}\right)} \times \frac{1}{(15-0.25)^2 \times 10^{-4} \mathrm{~m}^2}\)
= 4.13 × 106 NC-1 along BP
Field at P due to charge -10 μC
= \(\frac{10^{-5} \mathrm{C}}{4 \pi\left(8.854 \times 10^{-12} \mathrm{C}^2 \mathrm{~N}^{-1} \mathrm{~m}^{-2}\right)} \times \frac{1}{(15+0.25)^2 \times 10^{-4} \mathrm{~m}^2}\)
= 3.86 × 106 NC-1 along PA
The resultant electric field at P due to the two charges at A and B is 2.7 × 105 NC-1 along BP.
In this example, the ratio OP/OB is quite large (= 60). Thus, we can’expect to get approximately the same result as above by directly using the formula for electric field at a far-away point on the axis of a dipole. For a dipole consisting of charges ±q,.2a distance apart, the electric field at a distance r from the centre on the axis of the dipole has a magnitude.
E = \(\frac{2 \mathrm{p}}{4 \pi \varepsilon_0 \mathrm{r}^3}\) (r/a > > 1)
Where p = 2aq is the magnitude of the dipole moment.
The direction of electric field on the dipole axis is always along the direction of the dipole moment vector (i.e., from -q to q). Here, p = 10-5 × C ; 5 × 10-3 m = 5 × 10-8 C m
Therefore,
E = \(\frac{2 \times 5 \times 10^{-8} \mathrm{Cm}}{4 \pi\left(8.854 \times 10^{-12} \mathrm{C}^2 \mathrm{~N}^{-1} \mathrm{~m}^{-2}\right)} \times \frac{1}{(15)^3 \times 10^{-6} \mathrm{~m}^3}\)
= 2.6 × 105 N C-1
Along the dipolemoment direction AB, which is close to the result obtained earlier.
b) Field at Q due to charge +10 μC at B
= \(\frac{10^{-5} \mathrm{C}}{4 \pi\left(8.854 \times 10^{-12} \mathrm{C}^2 \mathrm{~N}^{-1} \mathrm{~m}^{-2}\right)} \times \frac{1}{\left(15^2+(0.25)^2\right] \times 10^{-4} \mathrm{~m}^2} \mathrm{x}\)
= 3.99 × 106 N C-1 along BQ
Field at Q due to charge – 10 μC at A
= \(\frac{10^{-5} \mathrm{C}}{4 \pi\left(8.854 \times 10^{-12} \mathrm{C}^2 \mathrm{~N}^{-1} \mathrm{~m}^{-2}\right)} \times \frac{1}{\left[15^2+(0.25)^2\right] \times 10^{-4} \mathrm{~m}^2}\)
= 3.99 × 106 × N C-1 along QA ‘
Clearly, the components of these two forces with equal magnitudes cancel along the direction OQ but add up along the direction parallel to BA. Therefore, the resultant electric field at Q due to the two charges at A and B is
= 2 × \(\frac{0.25}{\sqrt{15^2+(0.25)^2}}\) × 3.99 × 106NC-1 along BA
= 1.33 × 105 N C-1 along BA.
As in (a), we can expect to get approximately the same result by directly using the formula for dipole field at a point on the normal to the axis of the dipole :
E = \(\frac{\mathrm{p}}{4 \pi \varepsilon_0 \mathrm{r}^3}\) (r/a > > 1)
= \(\frac{5 \times 10^{-8} \mathrm{Cm}}{4 \pi\left(8.854 \times 10^{-12} \mathrm{C}^2 \mathrm{~N}^{-1} \mathrm{~m}^{-2}\right)} \times \frac{1}{(15)^3 \times 10^{-6} \mathrm{~m}^3}\)
= 1.33 × 105 N C-1
The direction of electric field in this case is opposite to the direction of the dipole moment vector. Again the result agrees with that obtained before.
![]()
Question 11.
The electric field components in Fig. are Ex = ax1/2, Ey = Ez = 0, in which a = 800 N/C m1/2. Calculate (a) the flux through the cube and (b) the charge within the cube. Assume that a = 0.1 m.
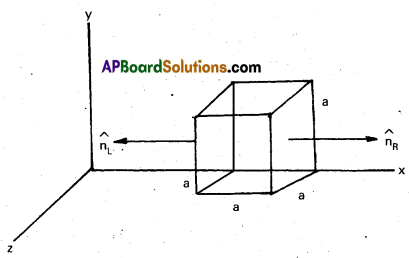
Solution:
a) Since the electric field has only an x component, for faces perpendicular to x direction, the angle between E and ∆S is ± π/2. Therefore, the flux Φ = E. ∆S is separately zero for each face of the cube except the two shaded ones. Now the magnitude of the electric field at the left face is EL = x1/2 = αa1/2
(x = a at the left face).
The magnitude of electric field at the right face is ER = αx1/2 = α(2a)1/2
(x = 2a at the right face).
The corresponding fluxes are
ΦL = EL . ∆S = ∆SEL . \(\hat{n}_L\) = EL ∆S cos θ = -EL ∆S, since θ = 180°
= -ELa2
ΦR = ER . ∆S = ER ∆S cos θ = ER ∆S, since θ = 0°
= ERa2
Net flux through the cube.
= ΦR + ΦL = ERa2 – ELa2 = a2 (ER – EL) = αa2 [(2a)1/2 – a1/2]
= αa5/2 (\(\sqrt{2}\) – 1)
= 800 (0.1)5/2 (\(\sqrt{2}\) – 1)
= 1.05 N m2 C-1
b) We can use Gauss’s law to find the total charge q inside the cube.
We have f = \(\frac{\mathrm{q}}{\varepsilon_0}\) or q = Φε0. Therefore,
q = 1.05 × 8.854 × 10-12 C = 9.27 × 10-27 C.
![]()
Question 12.
An electric field is uniform and in the positive x direction for positive x and uniform with the same magnitude but in the negative x direction for negative x. It is given that E = 200 \(\hat{\mathrm{i}}\) N/C for x > 0 and E = -200 \(\hat{\mathrm{i}}\) N/C for x < 0. A right circular cylinder of length 20 cm and radius 5 cm has its centre at the origin and its axis along the x-axis so that one face is at x = +10 cm and the other is at x = – 10 cm (Fig.),
(a) What is the net outward flux through each flat face ?
(b) What is the flux through the side of the cylinder ?
(c) What is the net outward flux through the cylinder ?
(d) What is the net charge inside the cylinder ?
Solution:
a) We can see from the figure that on the left face E and ∆S are parallel. Therefore, the outward flux is
ΦL = E. ∆S = -200 \(\hat{\mathrm{i}}\) . ∆S
= +200 ∆S, since \(\hat{\mathrm{i}}\) . ∆S = – ∆S
= +200 × π(0.05)2 = + 1.57 Nm2C-1
On the right face, E and AS are parallel and therefore
ΦR = E. ∆S = +1.57 Nm2C-1.
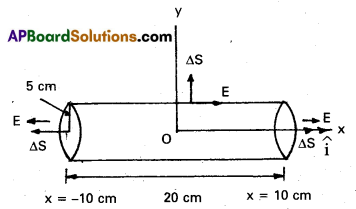
b) For any point on the side of the cylinder E is perpendicular to ∆S and hence E. ∆S = 0. Therefore, the flux out of the side of the cylinder is zero.
c) Net outward flux through the cylinder Φ = 1.57 + 1.57 + 0 = 3.14 Nm2C-1.
d) The net charge within the cylinder can be found by using Gauss’s law which gives
q = ε0Φ
= 3.14 × 8.854 × 10-12 C
= 2.78 × 10-11 C
Question 13.
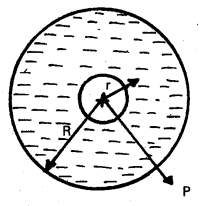
An early model for an atom considered it to have a positively charged point nucleus of charge Ze, surrounded by a uniform density of negative charge up to a radius R. The atom as a whole is neutral. For this model, what is the electric field at a distance r from the nucleus ?
Solution:
The charge distribution for this model of the atom is as shown in Fig. The total negative charge in the uniform spherical charge distribution of radius R must be -Ze, since the atom (nucleus of charge Z e + negative charge) is neutral.
This immediately gives us the negative charge density p, since we must have
\(\frac{4 \pi \mathrm{R}^3}{3}\) ρ = 0 – Ze or ρ = – \(\frac{3 \mathrm{Ze}}{4 \pi \mathrm{R}^3}\)
To find the electric field E(r) at a point P which is a distance r away from the nucleus, we use Gauss’s law. Because of the spherical symmetry of the charge distribution, the magnitude of the electric field E(r) depends only on the radial distance, no matter what the direction of r. Its direction is along (or opposite to) the radius vector r from the origin to the point P. The obviouis Gaussian surface is a spherical surface centred at the nucleus. We consider two situations, namely r < R and r > R.
![]()
i) r < R : The electric flux Φ enclosed by the spherical surface is Φ = E(r) × 4πr2
Where E(r) is the magnitude of the electric field at r. This is because the field at any point on the spherical Gaussian surface has the same direction as the normal to the surface there, and has the same magnitude at all points on the surface.
The charge q enclosed by the Gaussian surface is the positive nuclear charge and the negative charge within the sphere of radius r,
i.e., q = Ze + \(\frac{4 \pi \mathrm{r}^3}{3}\) ρ
Substituting for the charge density p obtained earlier, we have
q = Ze – Ze\(\frac{\mathrm{r}^3}{\mathrm{R}^3}\)
Gauss’s law then gives,
The electric field is directed radially outward.
ii) r > R: In this case, the total charge enclosed by the Gaussian spherical surface is zero since the atom is neutral. Thus, from Gauss’s law,
E(r) × 4 π r2 = 0 or E(r) = 0 ; r > R
At r = R, both cases give the same result: E = 0.