AP Inter 2nd Year Physics Important Questions Chapter 5 Electrostatic Potential and Capacitance

Students get through AP Inter 2nd Year Physics Important Questions 5th Lesson Electrostatic Potential and Capacitance which are most likely to be asked in the exam.

AP Inter 2nd Year Physics Important Questions 5th Lesson Electrostatic Potential and Capacitance

Short Answer Questions

Question 1.
Derive an expression for the electric potential due to a point charge. [T.S. Mar. 16]
Answer:
Expression for the electric potential due to a point charge:

1. Electric potential at a point is defined as the amount of workdone in moving a unit + ve charge from infinity to that point.
   
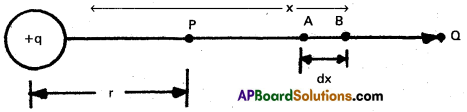
2. Consider a point P at a distance r from the point charge having charge + q. The electric field at P = E = \(\frac{q}{4 \pi \varepsilon_0 x^2}\)
3. Workdone in taking a unit +ve charge from B to A = dV = -E.dx (-ve sign shows that the workdone is +ve in the direction B to A, whereas the potential difference is +ve in the direction A to B.
4. Therefore, potential at P = The amount of workdone in taking a unit +ve charge from infinity to P
   

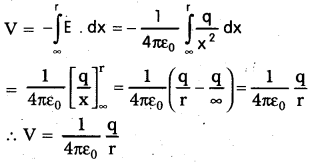
Question 2.
Derive an expression for the electrostatic potential energy of a system of two point charges and find its relation with electric potential of a charge.
Answer:
Expression for the electrostatic potential energy of a system of two point charges :

1. Let two point charges q₁ and q₂ are separated by distance ‘r’ in space.
2. An electric field will develop around the charge q₁.
3. To bring a charge q₂ from infinity to the point B some work must be done.
   
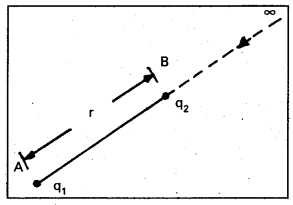
   Workdone = q₂ v_B
   But v_B = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1}{r}\)
   W = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}_1 \mathrm{q}_2}{\mathrm{r}}\)
4. This amount of workdone is stored as electrostatic potential energy (U) of a system of two charged particles. Its unit is joule.
   ∴ U = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}_1 \mathrm{q}_2}{\mathrm{r}}\)
5. If the two charges are similar then ‘U’ is positive. This is in accordance with the fact that two similar charges repel one another and positive work has to be done on the system to bring the charges nearer.
6. Conversely if the two charges are of opposite sign, they attract one another and potential energy is negative.

Question 3.
Derive an expression for the potential energy of an electric dipole placed in a uniform electric field.
Answer:
Expression for potential energy of an electric dipole placed in a uniform electric field :

1. Consider a electric dipole of length 2a having charges + q and -q.
2. The electric dipole is placed in uniform electric field E and it’s axis makes an angle θ with E.
3. Force on charges are equal but opposite sign. They constitute torque on the dipole.
   
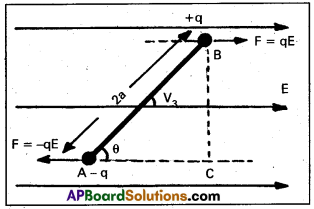
   Torque τ = one of its force (F) × ⊥^r distance (BC)
   F = qE and sinθ = \(\frac{\mathrm{BC}}{2 \mathrm{a}} \) ⇒ BC = 2a sinθ
   ∴ Torque τ = qE × 2a sinθ = PE sin θ [∴ p = 2aq]
4. Suppose the dipole is rotated through an angle dθ, the workdone dw is given by
   dw = τdθ = PE sinθ dθ
5. For rotating the dipole from angle θ₁ to θ₂
   workdone W = \(\int_{\theta_1}^{\theta_2}\) PE sinθdθ = PE(cosθ₁ – cosθ₂)
6. This workdone (W) is then stored as potential energy(U) in the dipole.
   ∴ U = PE(cosθ₁ – cosθ₂)
7. If θ₁ = 90° and θ₂ = 0°, U = – PE cos₁.
   In vector form U = –\(\overrightarrow{\mathrm{P}} \cdot \overrightarrow{\mathrm{E}}\)

Question 4.
Derive an expression for the capacitance of a parallel plate capacitor. [A.P. Mar. 16; T.S. Mar. 14]
Answer:
Expression for the capacitance of a parallel plate capacitor:

1. P and Q are two parallel plates of a capacitor separated by a distance of d.
2. The area of each plate is A. The plate P is charged and Q is earth connected.
3. The charge on P is + q and surface charge density of charge = σ
   ∴ q = Aσ
   
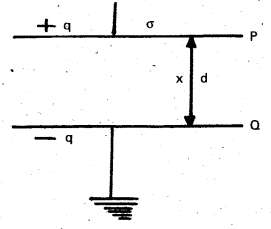
4. The electric intensity at point x , E = \(\frac{|\sigma|}{\varepsilon_0}\)
5. Potential difference between the plates P and Q,
   \(\int {\mathrm{dV}}=\int_{\mathrm{d}}^0-\mathrm{Edx}=\int_{\mathrm{d}}^0 \frac{-\sigma}{\varepsilon_0} \mathrm{dx}=\frac{\sigma \mathrm{d}}{\varepsilon_0}\)
6. Capacitance of the capacitor C = \(\frac{\mathrm{Q}}{\mathrm{V}}=\frac{\mathrm{A} \sigma}{\frac{\sigma \mathrm{d}}{\varepsilon_0}}=\frac{\varepsilon_0 \mathrm{~A}}{\mathrm{~d}}\) Farads (In air)
   Note : Capacity of a capacitor with dielectric medium is C = \(\frac{\varepsilon_0 \mathrm{~A}}{\left[\mathrm{~d}-\mathrm{t}+\frac{\mathrm{t}}{\mathrm{k}}\right]}\) Farads.

Question 5.
Explain the behaviour of dielectrics in an external field.
Answer:

1. When an external field is applied across dielectrics, the centre of positive charge distribution shifts in the direction of electric field and that of the negative charge distribution shifts
   
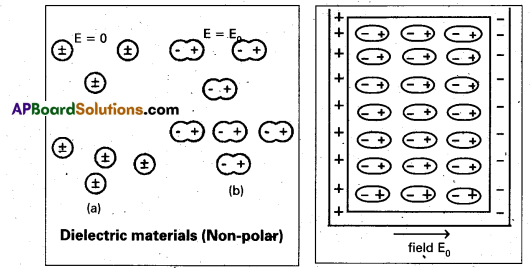
   opposite to the electric field and induce a net electric field within the medium opposite to the external field. In such situation the molecules are said to be polarised.
2. Now consider a capacitor with a dielectric between the plates. The net field in the dielectric becomes less.
3. If E₀ is the external field strength and E_i is the electric field strength induced, then the net field, \(\overrightarrow{\mathrm{E}}_{\text {net }}=\overrightarrow{\mathrm{E}}_0+\overrightarrow{\mathrm{E}}_{\mathrm{i}}\)
   (E_net) = E₀ – E_i = \(\frac{E}{K}\) where K is the dielectric constant of the medium.

Question 6.
Define electric potential. Derive an expression for the electric potential due to an electric dipole and hence the electric potential at a point (a) the axial line of electric dipole (b) on the equatorial line of electric dipole.
Answer:
Electric potential (V) : The workdone by a unit positive charge from infinite to a point in an electric field is called electric potential.

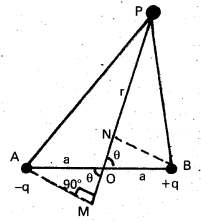
Expression for the potential at a point due to a dipole:

1. Consider A and B having -q and + q charges separated by a distance 2a.
2. The electric dipole moment P = q × 2a along AB
3. The electric potential at the point’P’is to be calculated.
4. P is at a distance ‘r’ from the point ‘O’. θ is the angle between the line OP and AB.
5. BN and AM are perpendicular to OP.
6. Potential at ‘P’ due to charge +q at B,
   V₁ = \(\frac{1}{4 \pi \varepsilon_0}\left[\frac{\mathrm{q}}{\mathrm{BP}}\right]\)
   ∴ V₁ = \(\frac{1}{4 \pi \varepsilon_0}\left[\frac{\mathrm{q}}{\mathrm{NP}}\right]\) [∵ BP = NP]
7. Potential at P due to charge -q at A, V₂ = \(\frac{1}{4 \pi \varepsilon_0}\left[\frac{\mathrm{-q}}{\mathrm{AP}}\right]\)
   ∴ V₂ = \(\frac{1}{4 \pi \varepsilon_0}\left[\frac{\mathrm{q}}{\mathrm{MP}}\right]\) [∵ AP = MP]
8. Therefore, Resultant potential at P is V = V₁ + V₂
   V = \(\frac{1}{4 \pi \varepsilon_0}\left[\frac{\mathrm{q}}{\mathrm{NP}}-\frac{\mathrm{q}}{\mathrm{MP}}\right]\) ………… (1)
9. In △le ONB, ON = OB cos0 = a cosθ; ∴NP = OP – ON = r – a cosθ ………………… (2)
10. In △le AMO, OM = AO cos0 = a cosθ; ∴ MP = MO + OP = r + a cosθ ………………. (3)
11. Substituting (2) and (3) in (1), we get
    
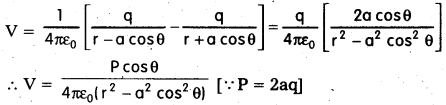
12. As r > >a, a² cos²θ can be neglected with comparision of r².
    ∴ V = \(\frac{\mathrm{P} \cos \theta}{4 \pi \varepsilon_0 \mathrm{r}^2}\)
13. (a) Electric potential on the axial line of dipole:
    
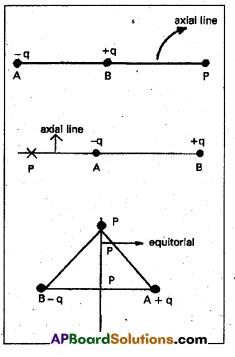
    • When θ = 0°, point p lies on the side of + q. ____
      ∴ V = \(\frac{\mathrm{P}}{4 \pi \varepsilon_0 \mathrm{r}^2}\) [∵ cos 0° = 1]
    • When θ = 180°, point p lies on the side of — q.
      ∴ V = \(\frac{\mathrm{-P}}{4 \pi \varepsilon_0 \mathrm{r}^2}\) [∵ cos 180° = -1]

Qeustion 7.
What is series combination of capacitors. Derive the formula for equivalent capacitance in series combination. [A.P.& T.S. Mar.15]
Answer:
Series combination : If a number of condensers are connected end to end between the fixed points then such combination is called series.
In this combination

1. Charge on each capacitor is equal.
2. P.D’s across the capacitors is not equal.

Consider three capacitors of capacitances C₁, C₂ and C₃ are connected in series across a battery of P.D V as shown in figure.

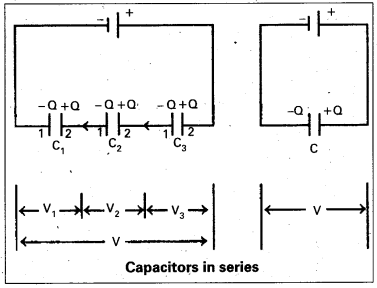
Let ‘Q’ be the charge on each capacitor.
Let V₁, V₂ and V₃ be the P.D’s of three
V = V₁ + V₂ + V₃ ……………… (1)
RD across I^st condenser V₁ = \(\frac{\mathrm{Q}}{\mathrm{C}_1}\)
RD across III^nd condenser V₂ = \(\frac{\mathrm{Q}}{\mathrm{C}_2}\)
RD across IIII^rd condenser V₃ = \(\frac{\mathrm{Q}}{\mathrm{C}_3}\)
∴ From the equation (1),V = V₁ + V₂ + V₃
= \(\frac{\mathrm{Q}}{\mathrm{C}_1}+\frac{\mathrm{Q}}{\mathrm{C}_2}+\frac{\mathrm{Q}}{\mathrm{C}_3}=\mathrm{Q}\left[\frac{1}{\mathrm{C}_1}+\frac{1}{\mathrm{C}_2}+\frac{1}{\mathrm{C}_3}\right]\)
\(\frac{\mathrm{V}}{\mathrm{Q}}=\frac{1}{\mathrm{C}_1}+\frac{1}{\mathrm{C}_2}+\frac{1}{\mathrm{C}_3}\)
\(\frac{1}{\mathrm{C}}=\frac{1}{\mathrm{C}_1}+\frac{1}{\mathrm{C}_2}+\frac{1}{\mathrm{C}_3}\) [∵ \(\frac{1}{C}=\frac{V}{Q}\)
For ‘n’ number of capacitors, the effective capacitance
\(\frac{1}{\mathrm{C}}=\frac{1}{\mathrm{C}_1}+\frac{1}{\mathrm{C}_2}+\frac{1}{\mathrm{C}_3}+\ldots+\frac{1}{\mathrm{C}_{\mathrm{n}}}\)

Question 8.
What is parallel combination of capacitors. Derive the formula for equivalent capacitance in parallel combination. [T.S. Mar. 17; A.P.& T.S. Mar. 15]
Answer:
Parallel Combination: The first plates of different capacitors are connected at one terminal and all the second plates of the capacitors are connected at another terminal then the two terminals are connected to the two terminals of battery is called parallel combination.

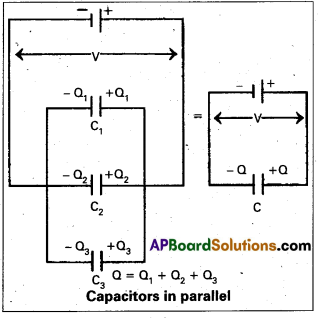
In this combination,
1. The P.D’s between each capacitor is equal (or) same.
2. Charge on each capacitor is not equal.
Consider three capacitors of capacitance C₁, C₂ and C₃ are connected in parallel across a P.D V as shown in fig.
The charge on Ist capacitor Q₁ = C₁ V
The charge on IInd capacitor Q₂ = C₂ V
The charge on IIIrd capacitor Q₃ = C₃ V
∴ The total charge Q = Q₁ + Q₂ + Q₃
= C₁ V + C₂ V + C₃ V
Q = V(C₁ + C₂ + C₃) ⇒ \(\frac{\mathrm{Q}}{\mathrm{V}}\) = C₁ + C₂ + C₃
C = C₁ + C₂ + C₃ [∵ C = \(\frac{\mathrm{Q}}{\mathrm{V}}\)]
for ‘n’ number of capacitors connected in parallel, the equivalent capacitance can be written as
C = C₁ + C₂ + C₃ + ……………. + C_n

Question 9.
Derive an expression for the energy stored in a capacitor.
Answer:
Expression for the energy stored in a capacitor : Consider an uncharged capacitor of capacitance ‘c’ and its initial will be zero. Now it is connected across a battery for charging then the final potential difference across the capacitor be V and final charge on the capacitor be ‘Q’
∴ Average potential difference V_A = \(\frac{\mathrm{O}+\mathrm{V}}{2}=\frac{\mathrm{V}}{2}\)
Hence workdone to move the charge Q = W = V_A × Q = \(\frac{\mathrm{VQ}}{2}\)
This is stored as electrostatic potential energy ‘U’
∴ U = \(\frac{\mathrm{QV}}{2}\)
We know Q = CV then ‘U’ can be written as given below.
U = \(\frac{\mathrm{QV}}{2}=\frac{1}{2}\) CV² = \(\frac{Q^2}{2 C}\)
∴ Energy stored in a capacitor
U = \(\frac{\mathrm{QV}}{2}=\frac{1}{2}\) CV² = \(\frac{1}{2} \frac{\mathrm{Q}^2}{\mathrm{C}}\)

Qeustion 10.
What is the energy stored when the space between the plates is filled with dielectric.
a) With charging battery disconnected ?
b) With charging battery connected in the circuit ?
Answer:
Effect of Dielectric on energy stored :
Case (a) : When the charging battery is disconnected from the circuit:
Let the capacitor is charged by a battery and disconnected from the circuit. Now the space between the plates is filled with a dielectric of dielectric constant ‘K’ then potential decreases by \(\frac{1}{\mathrm{~K}}\) times and charge remains constant.
Capacity increases by’K’ times.
New capacity C’ = \(\frac{Q}{V}\) = \(\frac{\frac{Q}{V}}{K}\) = K\(\frac{Q}{V}\) = KC [V’ = \(\frac{V}{K}\); C = \(\frac{Q}{V}\)]
∴ C’ = KC
Energy stored U’ = \(\frac{1}{2}\) QV = \(\frac{1}{2}\) Q \(\frac{V}{K}\) = \(\frac{U}{K}\)
U’ = \(\frac{U}{K}\)
∴ Energy stored decreases by \(\frac{1}{\mathrm{~K}}\) times.

Case (b) : When the charging battery is connected in the circuit:
Let the charging battery is continue the supply of charge. When the dielectric is introduced then potential decreases by \(\frac{1}{\mathrm{~K}}\) times and charge on the plates increases until the potential difference attains the original value = V
New charge on the plates Q’= KQ
Hence new capacity C’ = \(\frac{Q^{\prime}}{V}=\frac{K Q}{V}\) = KC
Energy stored in the capacitor U’ = \(\frac{1}{2}\) QV; = \(\frac{1}{2}\) (KQ) V = KU
U = KU
∴ Energy stored in the capacitor increases by ‘K times.

Problems

Question 1.
(a) Calculate the potential at a point P due to a charge of 4 × 10^-7 C located 9 cm away,
(b) Hence obtain the work done in bringing a charge of 2 × 10^-9 C from infinity to the point P. Does the answer depend on the path along which the charge is brought ?
Solution:
(a) V = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{Q}}{\mathrm{r}}\)
= 9 × 10⁹ Nm² C^-2 \(\frac{4 \times 10^{-7} \mathrm{C}}{0.09 \mathrm{~m}}\)
= 4 × 10⁴ V

(b) W = qV = 2 × 10^-9 C × 4 × 10⁴V
= 8 × 10^-5 J
No, work done will be path independent. Any arbitrary infinitesimal path can be resolved into two perpendicular displacements. One along r and another perpendicular to r. The work done corresponding to the later will be zero.

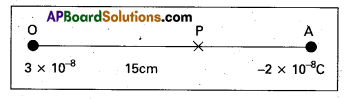
Qeustion 2.
Two charges 3 × 10^-8 C and -2 × 10^-8 C are located 15 cm apart. At what point on the line joining the two charges is the electric potential zero ? Thke the potential at infinity to be zero.
Solution:
Let us take the origin O at the location of the positive charge. The line joining the two charges is taken to be x-axis; the negative charge is taken to be on the right side of the origin fig.

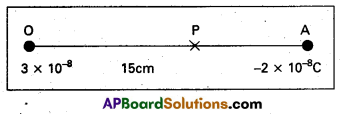
Let P be the required point on the x-axis where the potential is zero. If x is the x – coordinate of P, obviously x must be positive. (There is no possibility of potentials due to the two charges adding up to zero for x < 0.) If x lies between O and A, we have
\(\frac{1}{4 \pi \varepsilon_0}\left[\frac{3 \times 10^{-8}}{x \times 10^{-2}}-\frac{2 \times 10^{-8}}{(15-x) \times 10^{-2}}\right]\) = 0
where x is in cm. That is \(\frac{3}{x}-\frac{2}{15-x}\) = 0
which gives x = 9 cm
If x lies on the extended line OA, the required condition is \(\frac{3}{x}-\frac{2}{x-15}\) = 0
Which gives x = 45 cm
Thus, electric potential is zero at 9 cm and 45 cm away from the positive charge on the side of the negative charge. Note that the formula for potential used in the calculation required choosing potential to be zero at infinity.

Question 3.
A slab of material of dielectric constant K has the same area as the plates of a parallel plate capacitor but has a thickness (3/4)d, where d is the separation of the plates. How is the capacitance changed when die slab is inserted between the plates ?
Solution:
Let E₀ = V_g/d be the electric field between the plates when there is no dielectric and the potential difference is V₀. If the dielectric is now inserted, the electric field in the dielectric will be E = E₀/K. The potential difference will then be
V = \(E_0\left(\frac{1}{4} d\right)+\frac{E_0}{K}\left(\frac{3}{4} d\right)\)
= \(\mathrm{E}_0 \mathrm{~d}\left(\frac{1}{4}+\frac{3}{4 \mathrm{~K}}\right)=\mathrm{V}_0 \frac{\mathrm{K}+3}{4 \mathrm{~K}}\)
The potential difference decreases by the factor (K + 3)/K while the free charge Q₀ on the plates remains unchanged. The capacitance thus increases,
C = \(\frac{\mathrm{Q}_0}{\mathrm{~V}}=\frac{4 \mathrm{~K}}{\mathrm{~K}+3} \frac{\mathrm{Q}_0}{\mathrm{~V}_0}=\frac{4 \mathrm{~K}}{\mathrm{~K}+3} \mathrm{C}_0\)

Question 4.
Four charges are arranged at the corners of a square ABCD of side d. as shown in fig. Find the work required to put together this arrangement, (b) A charge q₀ is brought to the centre of the square, the four charges being held fixed at its comers. How much extra work is needed to do this ?

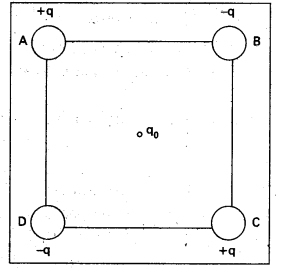
Solution:
(a) Since the work done depends on the final arrangement of the charges, and not on how they are put together, we calculate work needed for one way of putting the charges at A, B, C and D. Suppose, first the charge +q is brought to A and then the charges -q, +q, and -q are brought to B, C and D, respectively. The total work needed can be calculated in steps.

1. Work needed to bring charge +q to A when no charge is present elsewhere: this is zero.
2. Work needed to bring -q to B when + q is at A. This is given by (charge at B) × (electrostatic potential at B due to change +q at A) = -q × \(\left(\frac{q}{4 \pi \varepsilon_0 d}\right)\)
3. Work needed to bring charge +q to C when +q is at A and -q is at B. This is given by – (charge at Q × (potential at C due to charges at A and B) .
   
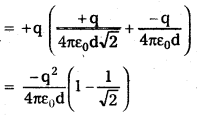
4. Work needed to bring -q to D when +q at A, -q at B, and +q at C.
   This is given by (charge at D) × (potential at D due to charges at A, B and C)
   
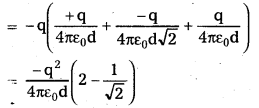
   Add the work done is steps (i), (ii), (iii) and (iv). The total work required is
   
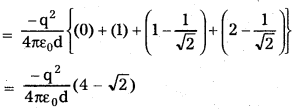
   The work done depends only on the arrangement of the charges, and not how they are assembled. By definition, this is the total electrostatic energy of the charges.
   (Students may try calculating same work/energy by taking charges in any other order they desire and convince themselves that the energy will remain the same.)

b) The extra work necessary to bring a charge q₀ to the point E when the four charges are at A, B, C and D is q₀ × (electrostatic potential at E due to the charges at A, B, C and D). The electrostatic potential at E is clearly zero since potential due to A and C is cancelled by that due to B and D.Hence no work is required to bring any charge to point E.

Question 5.
a) Determine the electrostatic potential energy of a system consisting of two charges 7μC and -2μC (and with no external field) placed at (-9 cm, 0,0) and (9cm, 0, 0) respectively.
b) How much work is required to separate the two charges infinitely away from each ‘ other?
Solution:
(a) U = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}_1 \mathrm{q}_2}{\mathrm{r}}\)
= 9 × 10⁹ × \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r}\) = -0.7 J.

(b)W = U₂ – U₁ = 0 – U = 0 – (-0.7)
= 0.7J.

Question 6.
There is a uniform electric field in the XOY plane represented by (\(40 \hat{\mathrm{i}}+30 \hat{\mathrm{j}}\)) Vm^-1. If the electric potential at the origin is 200 V, the electric potential at the point with coordinates (2m, 1m) is
Answer:
Given, uniform Electric field intensity,
\(\overrightarrow{\mathrm{E}}\) = (\(40 \hat{\mathrm{i}}+30 \hat{\mathrm{j}}\)) Vm^-1
Electric potential at the origin = 200V
Position vector \(\mathrm{d} \overrightarrow{\mathrm{r}}=(2 \hat{\mathrm{i}}+1 \hat{\mathrm{j}})\) m
We know that,

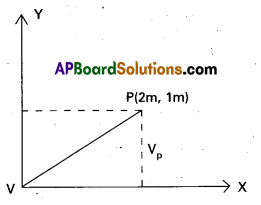
dV = \(-\vec{E} \cdot d \vec{r}=-(40 \hat{i}+30 \hat{j}) \cdot(2 \hat{i}+\hat{j})\)
V_p – V₀ = -(80 + 30) = -110Volt. ’
V_p = V₀ – 110 = (200 – 110) Volt = 90 Volt
∴ Potential at point P, V_p = 90Volt.

Question 7.
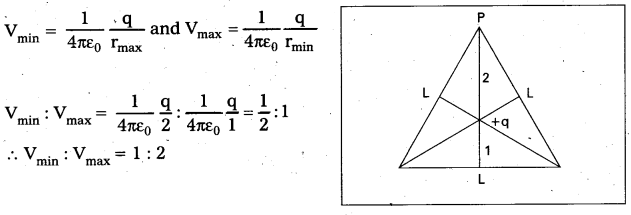
An equilateral triangle has a side length L. A charge +q is kept at the centroid of the triangle. P is a point on the perimeter of the triangle. The ratio of the minimum and maximum possible electric potentials for the point P is
Answer:
Charge at the centroid of an equilateral triangle = +q
The charge + q divides the line segment in ratio 2 : 1.
That means r_max = 2 and r_min = 1

Question 8.
A condenser of certain capacity is charged to a potential V and stores some energy. A second condenser of twice the capacity is to store half the energy of the first, find to what potential one must be charged ?
Solution:
(For first capacitor, C₁ = C; V₁ = V
And U₁ = \(\frac{1}{2}\) C₁V₁² = \(\frac{1}{2}\) CV² …………………. (1)
For second capacitor, C₂ = 2C₁ = 2C;
U₂ = \(\frac{\mathrm{U}_1}{2}=\frac{1}{4}\)CV²; Let potential difference across the capacitor = V₂

Then, U₂ = \(\frac{1}{2}\) C₂V₂²
⇒ \(\frac{1}{4}\) CV² = \(\frac{1}{2}\) × 2C × V₂²
⇒ V₂² = \(\frac{\mathrm{V}^2}{4}\)
∴ V₂ = \(\frac{V}{2}\)

Question 9.
Three Capacitors each of capaitance 9 pF are connected in series.
a) What is the total capacitance of the combination ?
b) What is the potential difference across each capacitor if the combination is connected to a 120 V supply ?
Solution:
a) Resultant capacitance in series combination \(\frac{1}{C_s}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3} \Rightarrow \frac{1}{C_S}=\frac{1}{9}+\frac{1}{9}+\frac{1}{9}=\frac{3}{9}=\frac{1}{3}\)
C_S = 3pF

b) Rd across each capacitor = \(\frac{\mathrm{V}}{3}=\frac{120}{3}\) = 40V

Question 10.
Three capacitors of capacitances 2 pF, 3 pF and 4 pF are connected in parallel. [A.P. Mar. 17]
a) What is the total capacitance of the combination ?
b) Determine the charge on each capacitor if the combination is connected to a 100 V supply.
Solution:
a) C_p = C₁ + C₂ + C₃ = 2 + 3 + 4 = 9pF
b) For each capacitor, V is same = 100 Volt
q₁ = C₁V = 2 × 100 = 200pC
q₂ = C₂V = 3 × 100 = 300pC
q₂ = C₃V = 4 × 100 = 400pC

Textual Examples

Question 1.
(a) Calculate the potential at a point P due to a charge of 4 × 10^-7C located 9 cm away.
(b) Hence obtain the work done in bringing a charge of 2 × 10^-9C from infinity to the point P. Does the answer depend on the path along which the charge is brought ?
Solution:
(a) V = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{Q}}{\mathrm{r}}\)
= 9 × 10⁹ Nm² C^-2 \(\frac{4 \times 10^{-7} \mathrm{C}}{0.09 \mathrm{~m}}\)
= 4 × 10⁴ V

(b) W = qV = 2 × 10^-9 C × 4 × 10⁴V
= 8 × 10^-5 J
No, work done will be path independent. Any arbitrary infinitesimal path can be resolved into two perpendicular displacements. One along r and another perpendicular to r. The work done corresponding to the later will be zero.

Question 2.
Two charges 3 × 10^-8 C and -2 × 10^-8C are located 15 cm apart. At what point on the line joining the two charges is the electric potential zero ? Take the potential at infinity to be zero.
Solution:
Let us take the origin O at the location of the positive charge. The line joining the two charges is taken to be x-axis; the negative charge is taken to be on the right side of the origin fig.

Let P be the required point on the x-axis where the potential is zero. If x is the x – coordinate of P, obviously x must be positive. (There is no possibility of potentials due to the two charges adding up to zero for x < 0.) If x lies between O and A, we have
\(\frac{1}{4 \pi \varepsilon_0}\left[\frac{3 \times 10^{-8}}{x \times 10^{-2}}-\frac{2 \times 10^{-8}}{(15-\mathrm{x}) \times 10^{-2}}\right]\) = 0
where x is in cm. That is \(\frac{3}{x}-\frac{2}{15-x}\) = 0
which gives x = 9 cm.
If x lies on the extended line OA, the required condition is \(\frac{3}{x}-\frac{2}{x-15}\) = 0
Which gives x. = 45 cm
Thus, electric potential is zero at 9 cm and 45 cm away from the positive charge on the side of the negative charge. Note that the formula for potential used in the claculation required choosing potential to be zero at infinity.

Question 3.
Figure (a) and (b) shows the field lines of a positive and negative point charge respectively.

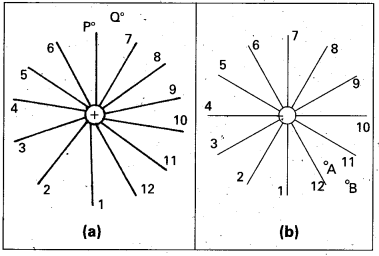
(a) Give the signs of the potential difference V_p – V_Q; V_B – V_A.
(b) Give the sign of the potential energy difference of a small negative charge between the points Q and P; A and B.
(c) Give the sign of the work done by the field in moving a small positive charge from Q to P.
(d) Give the sign of the work done by the external agency in moving a small negative charge from B And A.
(e) Does the kinetic energy of a small negative charge increase or decrease in going from B to A ?
Solution:
(a) As V ∝ \(\frac{1}{\mathrm{r}}\), V_p > V_Q. Thus, (V_p – V_Q) is positive. Also VB is less negative than V_A. Thus, V_B > V_A or (V_B – V_A) is positive.

(b) A small negative charge will be attracted towards positive charge. The negative charge moves from higher potential energy to lower potential energy. Therefore the sign of potential energy difference of a small negative charge between Q and P is positive. Similarly. (PE.)_A > (P.E.)_B and hence sign of potential energy differences is positive.

(c) In moving a small positive charge from Q to P, work has to be done by an external agency against the eletric field. Therefore, work done by the field is negative.

(d) In moving a small negative charge from B to A work has to be done by the external agency. It is positive.

(e) Due to force of repulsion on the negative charge, velocity decreases and hence the kinetic energy decreases in going form B to A.

Question 4.
Four charges are arranged at the comets of a square ABCD of side d. as shown in fig. 5.15.(a) Find the work required to put together this arrangement, (b) A charge q0 is brought to the centre of the square, the four charges being held fixed at its comers. How much extra work is needed to do this ?

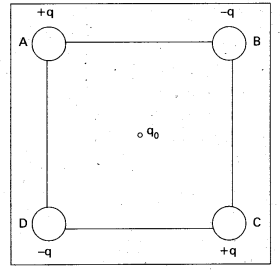
Solution:
(a) Since the work done depends on the final arrangement of the charges, and not on how they are put together, we calculate work needed for one way of putting the charges at A, B, C and D. Suppose, first the charge +q is brought to A, and then the charges -q, +q, and -q are brought to B, C and D, respectively The total work needed can be calculated in steps.

1. Work needed to bring charge +q to A when no charge is present elesewhere: this is zero.
2. Work needed to bring -q to B when +q is at A. This is given by (charge at B) x (electrostatic .potential at B due to charge +q at A) = -q × \(\left(\frac{\mathrm{q}}{4 \pi \varepsilon_0 \mathrm{~d}}\right)\)
3. Work needed to bring charge +q to C when +q is at A and -q is at B. This is given by – (charge at Q × (potential at C due to charges at A and B) .
   
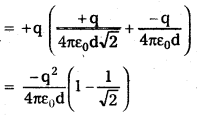
4. Work needed to bring -q to D when +q at A, -q at B, and +q at C.
   This is given by (charge at D) × (potential at D due to charges at A, B and C)
   
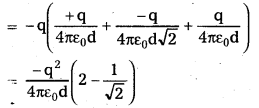
   Add the work done is steps (i), (ii), (iii) and (iv). The total work required is
   
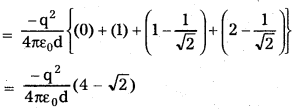
   The work done depends only on the arrangement of the charges, and not how they are assembled. By definition, this is the total electrostatic energy of the charges.
   (Students may try calculating same work/energy by taking charges in any other order they desire and convince themselves that the energy will remain the same.)

b) The extra work necessary to bring a charge q0 to the point E when the four charges are at A, B, C and D is q₀ × (electrostatic potential at E due to the charges at A, B, C and D). The electrostatic potential at E is clearly zero since potential due to A and C is cancelled by that due to B and D.Hence no work is required to bring any charge to point E.

Question 5.
a) Determine the electrostatic potential energy of a system consisting of two charges 7µC and -2µC (and with no external field) placed at (-9 cm, 0,0) and (9cm, 0, 0) respectively.
b) How much work is required to separate the two charges infinitely away from each other ?
c) Suppose that the same system of charges is now placed in an external electric field E = A(1/r²); A = 9 × 10⁵ C m^-2. What would the electrostatic energy of the configuration be ?
Solution:
(a) U = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}_1 \mathrm{q}_2}{\mathrm{r}}\)
= 9 × 10⁹ × \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r}\) = -0.7 J.

(b)W = U₂ – U₁ = 0 – U = 0 – (-0.7)
= 0.7J.

c) The mutual interaction energy of the two charges remains unchanged. In addition, there is the energy of interaction of the two charges with the external electric field. We find,
q₁V(r₁) + q₂V(r₂) = A \(\frac{7 \mu \mathrm{C}}{0.09 \mathrm{~m}}\) + A \(\frac{-2 \mu \mathrm{C}}{0.09 \mathrm{~m}}\)
and the net electrostatic energy is
q₁V(r₁) + q₂V(r₂) + \(\frac{q_1 q_2}{4 \pi \varepsilon_0 r_{12}}\)
= A \(\frac{7 \mu \mathrm{C}}{0.09 \mathrm{~m}}\) + A \(\frac{-2 \mu \mathrm{C}}{0.09 \mathrm{~m}}\)
= 70 – 20 – 0.7 = 49.3J

Question 6.
A molecule of a substance has a perma-nent electric dipole moment of magnitude 10^-29C m. A mole of this substance is polarised (at low temperature) by applying a strong electrostatic field of magnitude 10⁶ V m^-1. The direction of the field is suddenly changed by an angle of 60°. Estimate the heat released by the substance in aligning its dipoles along the new direction of the field. For simplicity, assume 100% polarisation of the sample.
Solution:
Here, dipole moment of each molecules = 10^-29C m
As 1 mole of the substance contains 6 × 10²³ molecules,
total dipole moment of all the molecules, p = 6 × 10²³ × 10^-29 Cm
= 6 × 10^-6 C m
Initial potential energy, U_t = -pE cos θ
=-6 × 10^-6 × 10⁶ cos 0° = -6 J
Final potential energy (when θ = 60°),
U_f = -6 × 10^-6 × 10⁶ × cos 60° = – 3J
Change in potential energy
= -3 J – (-6j) = 3 J
So, there is loss in potential energy. This must be the energy released by the substance in the form of heat in aligning its dipoles.

Question 7.
(a) A comb run through one’s dry hair attracts small bits of paper. Why ? What happens if the hair is wet or if it is a rainy day ? (Remember, a paper does not conduct electricity.)
(b) Ordinary rubber is an insulator. But special rubber types of aircraft are made slightly conducting. Why is this necessary ?
(c) Vehicles carrying inflammable materials usually have metallic ropes touching the ground during motion. Why?
(d) A bird perches on a bare high power line, and nothing happens to the bird. A man standing on the ground touches the same line and gets a fatal shock. Why ?
Solution:
(a) This is because the comb gets charged by friction. The molecules in the paper gets polarised by the charged comb, resulting in a net force of attraction, if the hair is wet, or if it is a rainy day. friction between hair and the comb reduces. The comb does not get charged and thus it will not attract small bits of paper.

(b) To enable them to conduct charge (produced by friction) to the ground; as too much of static electricity accumulated may result in spark and result in fire.

(c) Reason similar to (b).

(d) Current passes only when there is difference in potential.

Question 8.
A slab of material of dielectric constant K has the same area as the plates of a parallelplate capacitor but has a thickness (3/4)d, where d is the separation of the plates. How is the capacitance changed when the slab is inserted between the plates ?
Solution:
Let E₀ = V_g/d be the electric field between the plates when there is no dielectric and the potential difference is V₀. If the dielectric is now inserted, the electric field in the dielectric will be E = E₀/K. The potential difference will then be
V = \(E_0\left(\frac{1}{4} d\right)+\frac{E_0}{K}\left(\frac{3}{4} d\right)\)
= \(\mathrm{E}_0 \mathrm{~d}\left(\frac{1}{4}+\frac{3}{4 \mathrm{~K}}\right)=\mathrm{V}_0 \frac{\mathrm{K}+3}{4 \mathrm{~K}}\)
The potential difference decreases by the factor (K + 3)/K while the free charge Q₀ on the plates remains unchanged. The capacitance thus increases,
C = \(\frac{\mathrm{Q}_0}{\mathrm{~V}}=\frac{4 \mathrm{~K}}{\mathrm{~K}+3} \frac{\mathrm{Q}_0}{\mathrm{~V}_0}=\frac{4 \mathrm{~K}}{\mathrm{~K}+3} \mathrm{C}_0\)

Question 9.
A network of four 10μF capacitors is connected to a 500V supply, as shown in Fig. Determine
(a) the equivalent capacitance of the network and
(b) the charge on each capacitor, (Note, the charge on a capacitor is the charge on the plate with higher potential, equal and opposite to the charge on the plate with lower potential.)

Solution:
(a) In the given network, C₁, C₂ and C₃ are connected in series. The effective capacitance C’ of these three capacitors isgivgftby
\(\frac{1}{\mathrm{C}^{\prime}}=\frac{1}{\mathrm{C}_1}+\frac{1}{\mathrm{C}_2}+\frac{1}{\mathrm{C}_3}\)
For C₁ = C₂ = C₃ = 10 μF. C = (10/3) μF. The network has C and C₄ connected in parallel. Thus, the equivalent capacitance C of the network is
C = C’ + C₄ = (\(\frac{10}{3}\) + 10) μF = 13.3 μF

(b) Clearly, from the figure, the charge on each of the capacitors, C₁, C₂ and C₃ is the same, say Q. Let the charge on C₄ be Q. Now, since the potential difference c across AB is Q/C₁ across BC is Q/C₂. across CD is Q/C₃, we have
\(\frac{\mathrm{Q}}{\mathrm{C}_1}+\frac{\mathrm{Q}}{\mathrm{C}_2}+\frac{\mathrm{Q}}{\mathrm{C}_3}\) = 500 V
Also Q’/C₄ = 500V.
This gives for the given value of the capacitances,
Q = 500 V × \(\frac{10}{3}\) μF = 1.7 × 10^-3C and
Q’ = 500 V × 10μF = 5.0 × 10^-3C

Question 10.
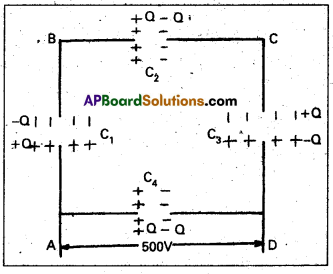
(a) A 900pF capacitor is charged by 100 V battery [Fig.a]. How much electrostatic energy is stored by the capacitor ?
(b) The capacitor is disconnected from the battery and connected to another 900 pF capacitor. What is the electrostatic y energy stored by the system ?

Solution:
The charge on the capacitor is
Q = CV = 900 × 10^-12F × 100 V
= 9 × 10^-8C
The energy stored by the capacitor is
= (1/2) CV² = (1/2) QV
= (1/2) × 9 × 10^-8C × 100 V
= 4.5 × 10^-6 J

(b) In the steady situation, the two capacitors have their positive plates at the same potential, and their negative plates at the same potential. Let the common potential difference be V. The charge on each capacitor is then Q’ = CV’. By charge conservation, Q’ = Q/2. This implies V’ = V/2. The total energy of the system is
= 2 × \(\frac{1}{2}\)Q’V’ = \(\frac{1}{4}\)QV = 2.25 × 10⁶J
Thus in going from (a) to (b), though no charge is lost; the final energy is only half the initial energy. Where has the remaining energy gone ?
There is a transient period before the system settles to the situation (b). During this period, a transient current flows from the first capacitor to the second. Energy is lost during this time in the form of heat and electromagnetic radiation.