AP Inter 2nd Year Physics Study Material Chapter 1 తరంగాలు

Andhra Pradesh BIEAP AP Inter 2nd Year Physics Study Material 1st Lesson తరంగాలు Textbook Questions and Answers.

AP Inter 2nd Year Physics Study Material 1st Lesson తరంగాలు

అతిస్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
తరంగం ఏమి సూచిస్తుంది?
జవాబు:
యానకం స్థానాంతరణ లేకుండా, ఒక బిందువు నుండి మరియొక బిందువుకు శక్తి ప్రసారంను యానకం సూచిస్తుంది.

ప్రశ్న 2.
తిర్యక్, అనుదైర్ఘ్య తరంగాల మధ్య భేదాన్ని గుర్తించండి.
జవాబు:

తిర్యక్ తరంగాలు	అనుదైర్ఘ్య తరంగాలు
1. యానకంలోని కణాలు, తరంగ ప్రసారదిశకు లంబంగా కంపిస్తాయి.	1. యానకంలోని కణాలు, తరంగ ప్రసారదిశకు సమాంతరంగా కంపిస్తాయి.
2. శృంగాలు మరియు ద్రోణులు ఏర్పడతాయి.	2. సంపీడనాలు మరియు విరళీకరణాలు ఏర్పడతాయి.

ప్రశ్న 3.
ఒక పురోగామి హరాత్మక తరంగాన్ని వర్ణించడానికి ఉపయోగించే పరామితులు ఏమిటి?
జవాబు:
పురోగామి తరంగ సమీకరణం y = a sin (ωt – kx), ఇక్కడ ω = 2πν = \(\frac{2 \pi}{T}\); k = \(\frac{2 \pi}{\lambda}\)

పరామితులు :
1) a = కంపన పరిమతి 2) λ = తరంగదైర్ఘ్యం 3) T = ఆవర్తన కాలం 4) ν = పౌనఃపున్యం 5) k = ప్రసార స్థిరాంకం 6) ω = కోణీయ పౌనఃపున్యం.

ప్రశ్న 4.
ఈ పరామితుల పదాలలో తరంగవేగానికి ఒక సమాసాన్ని పొందండి.
జవాబు:
తరంగవేగము ” పౌనఃపున్యం ‘ν’ మరియు తరంగదైర్ఘ్యం ‘λ’. డోలనావర్తన కాలం ‘T’ అయితే,
అప్పుడు ν = \(\frac{1}{T}\)
కాలం ‘T’ లో తరంగం ప్రయాణించిన దూరం = λ.
1 సెకనులో ప్రయాణించిన దూరం = \(\frac{\lambda}{T}\)
ఇది తరంగ వేగంనకు సమీకరణం ∴ υ = νλ

ప్రశ్న 5.
మితీయ విశ్లేషణను ఉపయోగించి ఒక సాగదీసిన తంత్రిలో తిర్యక్ తరంగాల వడికి ఒక సమాసాన్ని పొందండి.
జవాబు:
తరంగ వేగం v α T^a µ^b ⇒ v =K T^a µ^b → (1)
v మితులు = M°L¹T^-1, తన్యత T = M¹L¹T^-2
రేఖీయ ద్రవ్యరాశి µ = M¹L^-1, స్థిరాంకం K = M°L°T°
ఇప్పుడు (1)వ సమీకరణం M°L¹L^-1 = [M¹L¹T^-2]^a [M¹L^-1]^b
M°L¹T¹ = M^a+b L^a-b T^-2a
ఒకే భౌతికరాశి ఘాతాలను పోల్చగా,

ప్రశ్న 6.
మితీయ విశ్లేషణను ఉపయోగించి ఒక యానకంలో ధ్వని తరంగాల వడికి ఒక సమాసాన్ని పొందండి.
జవాబు:
ధ్వని వేగం v α B^aρ^b = v =KB^aρ^b → (1)
v మితులు = M°L¹T^-1, యానకం స్థితిస్థాపకత

ప్రశ్న 7.
తరంగాల అధ్యారోపణ సూత్రం అంటే ఏమిటి?
జవాబు:
ఒక యానకంలోని రెండు లేక మూడు తరంగాలు వరుసగా ఒక కణంపై పనిచేస్తే, ఫలిత స్థానభ్రంశం వైయక్తిక తరంగాల స్థానభ్రంశాల మొత్తంనకు సమానము.

y₁, y₂, y₃, ……….. లు కణం వైయక్తిక స్థానభ్రంశాలు అయితే, ఫలిత స్థానభ్రంశము y = y₁ + y₂ + …………….. + y_n.

ప్రశ్న 8.
ఏ నిబంధనలకు లోబడి ఒక తరంగం పరావర్తనం చెందుతుంది?
జవాబు:

1. ఏదైనా బిందువు వద్ద యానకం చివర మారితే
2. ఏదైనా బిందువు వద్ద యానకం సాంద్రత మరియు దృఢతా గుణకం మారిన తరంగాలు పరావర్తనం చెందుతాయి.

ప్రశ్న 9.
తరంగం దృఢ సరిహద్దు వద్ద పరావర్తనం చెందితే, పతన, పరావర్తిత తరంగాల మధ్య దశా భేదం ఎంత ?
జవాబు:
π రేడియన్ లేక 180°.

ప్రశ్న 10.
స్థావర లేదా స్థిర తరంగం అంటే ఏమిటి?
జవాబు:
రెండు ఒకే రకమైన పురోగామి (తిర్యక్ లేక అనుదైర్ఘ్య తరంగాలు, యానకంలో సరళరేఖలో వ్యతిరేక దిశలలో ప్రయాణిస్తూ అధ్యారోపణం చెందితే, స్థిర తరంగాలు ఏర్పడతాయి.

ప్రశ్న 11.
అస్పందన, ప్రస్పందన పదాల వల్ల మీరు ఏమి అర్థం చేసుకొన్నారు?
జవాబు:
అస్పందన స్థానం :
కణం శూన్య కంపన పరిమితి స్థానంను అస్పందన స్థానం అంటారు.

ప్రస్పందన స్థానం :
కణం గరిష్ఠ కంపన పరిమితి స్థానంను ప్రస్పందన స్థానం అంటారు.

ప్రశ్న 12.
ఒక స్థిర తరంగంలో ఒక అస్పందన, ఒక ప్రస్పందనల మధ్య దూరం ఎంత?
జవాబు:
అస్పందన మరియు ప్రస్పందన స్థానాల మధ్య దూరం = \(\frac{\lambda}{4}\)

ప్రశ్న 13.
సహజ పౌనఃపున్యం లేదా సామాన్య కంపనరీతితో మీరు ఏమి అర్థం చేసుకొన్నారు?
జవాబు:
ఒక వస్తువును స్వేచ్ఛగా కంపించేటట్లు చేసి వదిలితే, ఆ వస్తు కంపనాలను స్వేచ్ఛా లేక సహజ కంపనాలు అంటారు. ఆ వస్తు పౌనఃపున్యంను సహజ పౌనఃపున్యం లేక సాధారణరీతి కంపనం అంటారు.

ప్రశ్న 14.
అనుస్వరాలు అంటే ఏమిటి?
జవాబు:
స్థిర తరంగాలు ఏర్పడే పౌనఃపున్యాలను అనుస్వరాలు అంటారు. (లేక) ప్రాథమిక పౌనఃపున్యాల సహజ గుణిజాలను అనుస్వరాలు అంటారు.

ప్రశ్న 15.
రెండు దృఢ ఆధారాల మధ్య ఒక తంత్రి సాగదీయడమైంది. అటువంటి తంత్రిలో సాధ్యమయ్యే కంపన పౌనఃపున్యాలు ఏవి?
జవాబు:
రెండు దృఢ ఆధారాల మధ్య సాగదీసిన తంత్రి (తీగ)లో సాధ్యమగు కంపనాల పౌనఃపున్యాలను యిచ్చు సమీకరణము

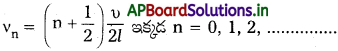
ప్రశ్న 16.
ఒక చివర మూసిన పొడవైన గొట్టంలో గాలి స్తంభాన్ని కంపింపచేస్తే సాధ్యమయ్యే అనుస్వరాలు ఏమిటి?
జవాబు:
ఒక పొడవాటి మూసిన గొట్టంలో గాలిస్థంభ కంపనంలో సాధ్యమగు అనుస్వరాలను యిచ్చు సమీకరణము
v_n = [2n +1] \(\frac{υ}{4l}\) ఇక్కడ n = 0, 1, 2, 3, ………….

ప్రశ్న 17.
రెండువైపుల తెరచిన ఒక గొట్టంలోని గాలి స్తంభాన్ని కంపింపచేస్తే సాధ్యమయ్యే అనుస్వరాలు ఏమిటి?
జవాబు:
ఒక తెరిచిన గొట్టంలో గాలి స్తంబ కంపనంలో సాధ్యమగు అనుస్వరాలను యిచ్చు సమీకరణము
v_n = \(\frac{nυ}{2l}\) ఇక్కడ n = 1, 2, 3, ………………

ప్రశ్న 18.
విస్పందనాలు అంటే ఏమిటి?
జవాబు:
విస్పందనాలు :
సమీప పౌనఃపున్యం ఉన్న రెండు ధ్వని తరంగాలు ఒకే దిశలో చలిస్తూ, వ్యతికరణం చెందితే, క్రమ కాల వ్యవధులలో ధ్వని వృద్ధి మరియు క్షీణత ఉండును. ఈ దృగ్విషయంను “విస్పందనాలు” అంటారు.

ప్రశ్న 19.
విస్పందన పౌనఃపున్యం కోసం ఒక సమాసాన్ని వ్రాయండి. దానిలో ఉండే పదాలను వివరించండి.
జవాబు:
విస్పందన పౌనఃపున్య సమీకరణం, ∆ν = ν₁ ~ ν₂
ఇక్కడ v₁ మరియు v₂ లు రెండు తరంగాల పౌనఃపున్యాలు.

ప్రశ్న 20.
డాప్లర్ ప్రభావం అంటే ఏమిటి? ఒక ఉదాహరణ ఇవ్వండి.
జవాబు:
డాప్లర్ ప్రభావం :
ధ్వని జనకం మరియు పరిశీలకుని మధ్య సాపేక్ష చలనం ఉన్నప్పుడు, పరిశీలకుడు వినే దృశ్య పౌనః పున్యంలోని మార్పును, డాప్లర్ ప్రభావం అంటారు.
ఉదా : ఈల వేస్తున్న రైలు, ఫ్లాట్ఫాంపై నిల్చున్న పరిశీలకుని సమీపిస్తూ ఉంటే, దృశ్య పౌనఃపున్యం పెరుగును. దూరంగా చలిస్తే, దృశ్య పౌనఃపున్యం తగ్గును.

ప్రశ్న 21.
జనకం, పరిశీలకుడు ఒకదానితో మరొకటి సాపేక్షంగా ఒకే దిశలో చలిస్తున్నప్పుడు పరిశీలించిన పౌనఃపున్యానికి ఒక సమాసాన్ని వ్రాయండి.
జవాబు:
పరిశీలకుడు వినే దృశ్య పౌనఃపున్యం,

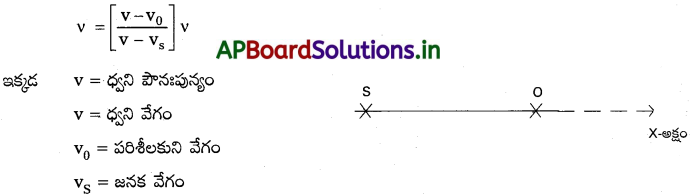
స్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
తిర్యక్ తరంగాలు అంటే ఏమిటి? అటువంటి తరంగాలకు వివరణాత్మకమయిన ఉదాహరణలు ఇవ్వండి.
జవాబు:
తిర్యక్ తరంగాలు :
కణాల కంపనము మరియు తరంగ ప్రసార దిశ ఒకదానికొకటి లంబంగా ఉంటే, ఆ తరంగాలను తిర్యక్ తరంగాలు అంటారు.

1. సాగదీసిన తంత్రి (తీగ)లో ఏర్పడు తరంగాలు తిర్యక్ తరంగాలు.
2. సాగదీసిన తంత్రిని తాకితే, దాని వెంట తిర్యక్ తరంగాలు ఏర్పడతాయి.
3. తంత్రిలో కణాలు తరంగ ప్రసార దిశకు లంబంగా కంపిస్తాయి.
4. తిర్యక్ తరంగాలు ఘన పదార్థంలో మరియు ద్రవం ఉపరితలంపై ప్రసారమవుతాయి.
   ఉదా : కాంతి తరంగాలు, ఉపరితల జల తరంగాలు.

ప్రశ్న 2.
అనుదైర్ఘ్య తరంగాలు అంటే ఏమిటి? అటువంటి తరంగాలకు వివరణాత్మక ఉదాహరణలు ఇవ్వండి.
జవాబు:
అనుదైర్ఘ్య తరంగాలు:
తరంగ ప్రసార దిశ మరియు కణాల కంపన దిశలు, ఒకే దిశలో ఉంటే, ఆ తరంగాలను అనుదైర్ఘ్య తరంగాలు అంటారు.

1. ఒక సంపీడన స్ప్రింగ్న, వదిలితే అనుదైర్ఘ్య తరంగాలు ఏర్పడతాయి.
2. స్ప్రింగ్ వెంట సంపీడన మరియు విరళీకరణాలు ప్రసారమవుతాయి.
   
   C = సంపీడనం; R = విరళీకరణం.
3. అవి ఘన, ద్రవ మరియు వాయువుల గుండా ప్రయాణిస్తాయి.
   ఉదా : ధ్వని తరంగాలు.

ప్రశ్న 3.
పురోగామి హరాత్మక తరంగానికి సమాసాన్ని వ్రాయండి. ఆ సమాసంలో ఉపయోగించిన విభిన్న పరామితులను వివరించండి.
జవాబు:
పురోగామి అనుస్వర తరంగ సమీకరణం

పరామితులు:
1) కంపన పరిమితి (a) :
మాధ్యమిక స్థానం నుండి కంపన కణం గరిష్ట స్థానభ్రంశంను కంపన పరిమితి అంటారు.

2) పౌనఃపున్యం (V) :
కంపిస్తున్న వస్తువు ఒక సెకనులో చేయు పూర్తి కంపనాల సంఖ్యను పౌనఃపున్యం అంటారు.

3) తరంగదైర్ఘ్యం (λ) :
ఒక తరంగము ఒక పూర్తి కంపనంలో ప్రయాణించు దూరంను తరంగదైర్ఘ్యం అంటారు. (లేక) రెండు వరుస బిందువులు ఒకే దశలో ఉన్నప్పుడు వాని మధ్య దూరంను తరంగదైర్ఘ్యం అంటారు.

4) కంపన దశ (Φ) :
ఏదైనా క్షణాన కంపిస్తున్న కణం యొక్క స్థానభ్రంశ స్థితిని, ఆ కణం యొక్క కంపన దశ అంటారు. ఇది దశా కోణంను ఇస్తుంది.

ప్రశ్న 4.
ఒక సాగదీసిన తంత్రి కంపన రీతులను ఉదాహరణలతో వివరించండి.
జవాబు:

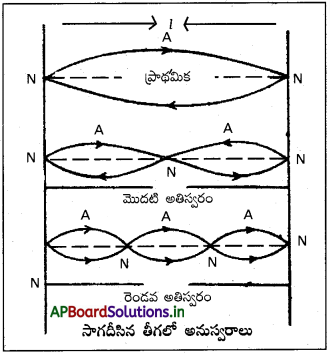
సాగదీసిన తీగలో కంపన రీతులు:
1) ఒక సాగదీసిన తంత్రి వేర్వేరు పౌనఃపున్యాల వద్ద కంపిస్తే, స్థిర తరంగాలు ఏర్పడతాయి. ఈ కంపన రీతులను అనుస్వరాలు అంటారు.

2) తంత్రి ఒక భాగంగా కంపిస్తే, దానిని ప్రాథమిక అనుస్వరం అంటారు. ఎక్కువ అనుస్వరాలను అతిస్వరాలు అంటారు.

3) తంత్రి రెండు భాగాలుగా కంపిస్తే, రెండవ అనుస్వరంను శ్రీ మొదటి అతి స్వరం అంటారు. ఇదేవిధంగా కంపనాల వరుస పటంలో చూపబడినవి.

4) సాగదీసిన తంత్రి P భాగాలుగా (ఉచ్చులుగా) కంపిస్తే,


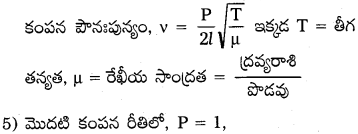
అనుస్వరాల పౌనఃపున్యాల నిష్పత్తి ν : ν₁ : ν₂ = ν : 2ν : 3ν = 1 : 2 : 3

ప్రశ్న 5.
ఒక తెరిచిన గొట్టంలోని గాలిస్తంభపు కంపనాల రీతులను వివరించండి. [A.P (Mar.’17)]
జవాబు:
తెరిచిన గొట్టంలో గాలిస్తంభ కంపన రీతులు :

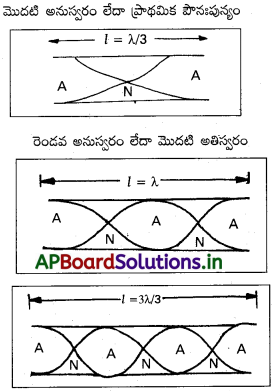
1. తెరిచిన గొట్టం రెండువైపులా తెరిచి ఉండును. తెరిచిన చివరల వద్ద ప్రస్పందన స్థానాలు ఏర్పడును. వాని మధ్య అస్పందన స్థానం ఏర్పడును.
2. తెరిచిన గొట్టంలో కంపిస్తున్న గాలిస్తంభంలో సాధ్యమగు అనుస్వరాలు, ν = \(\frac{nυ}{2l}\)
   ఇక్కడ n = 1, 2, 3
3. మొదటి కంపన రీతిలో, n = 1 అప్పుడు v₁ = \(\frac{υ}{2l}\)
   (మొదటి అనుస్వరం లేక ప్రాథమిక పౌనఃపున్యం).
4. రెండవ కంపన రీతిలో, n = 2 అప్పుడు v₂ = \(\frac{2υ}{2l}\)
   (రెండవ అనుస్వరం లేక మొదటి అతిస్వరం).
5. మూడవ కంపన రీతిలో, n = 3 అప్పుడు v₃ = \(\frac{3υ}{2l}\)
   (మూడవ అనుస్వరం లేక రెండవ అతిస్వరం).
6. తెరిచిన గొట్టంలో అనుస్వరాల’ పౌనఃపున్యాల నిష్పత్తి
   v₁ : v₂ : v₃ = v : 2v : 3v = 1 : 2 : 3

ప్రశ్న 6.
అనునాదం అంటే మీరు ఏమి అర్థం చేసుకొన్నారు? గాలిలో ధ్వని వేగాన్ని కనుక్కోవడానికి అనునాదాన్ని మీరెలా ఉపయోగిస్తారు?
జవాబు:
అనునాదం :
కంపిస్తున్న వస్తు సహజ పౌనఃపున్యము, బాహ్య ఆవర్తన బలం పౌనఃపున్యంనకు సమానం అయితే, ఆ రెండు వస్తువులు అనునాదంలో ఉన్నాయంటారు. అనునాదం వద్ద వస్తువులు పెరుగుతున్న కంపన పరిమితితో కంపిస్తాయి.

అనునాదంను ఉపయోగించి గాలిలో ధ్వనివేగంను నిర్ణయించుట:

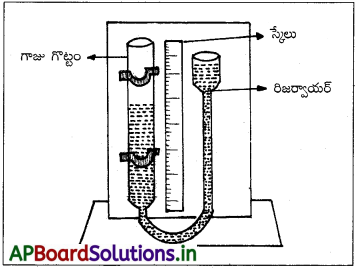
1) అనునాద గొట్టంలో, గాలిస్తంభం కంపిస్తున్న శృతిదండాంలో కంపిస్తుంది. నిర్ధిష్ట గాలిస్తంభం పొడవు వద్ద, పౌనఃపున్యంనకు సమానమైన పౌనఃపున్యం వద్ద గాలి స్తంభం కంపిస్తుంది. అప్పుడు గాలిస్తంభం, గరిష్ఠ కంపన పరిమితి మరియు తీవ్రతతో ధ్వని ఏర్పడును.
2) తెరిచిన గొట్టం పైన తెలిసిన పౌనఃపున్యం (ν) ఉన్న కంపిస్తున్న శృతిదండాన్ని ఉంచుదాము.
3) గాలిస్తంభం పొడవును క్రమంగా పెంచితే, రెండు వేర్వేరు గాలిస్తంభ పొడవుల వద్ద ఎక్కువ శబ్దం (booming sound) వినిపిస్తుంది.
4) మొదటి అనునాదంలో, గాలిస్తంభ పొడవు l, అయితే, అప్పుడు
\(\frac{\lambda}{4}\) = l₁ + C ………….. (1)

ఇక్కడ λ ఉరించు ధ్వని తరంగదైర్ఘ్యం మరియు c గొట్టం తుది సవరణ.

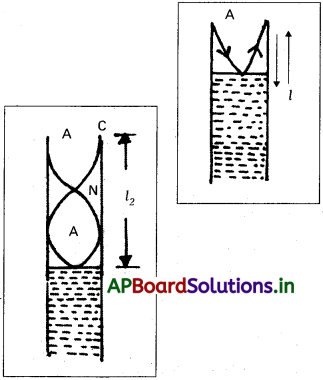
5) రెండవ అనునాదంలో, గాలి స్తంభం పొడవు l₁ అయితే,
అప్పుడు \(\frac{3 \lambda}{4}\) = l₂ + C ………….(2)
(2) – (1) ⇒ \(\frac{\lambda}{2}\) = l₂ – l₁
λ = 2 (l₂ – l₁)

ధ్వని వేగం, v = v2(l₁ – l₁)
∴ v = 2v (l₂ – l₁)

6) v₁, l₁, l₂ లు తెలిసిన ధ్వని వేగంను గణిస్తారు.

ప్రశ్న 7.
స్థిర తరంగాలు అంటే ఏమిటి? ఒక సాగదీసిన తంత్రిలో స్థిర తరంగాలు ఏవిధంగా ఏర్పడతాయో వివరించండి.
జవాబు:
స్థిర తరంగాలు లేక స్థావర తరంగాలు:
రెండు సర్వ సమ పురోగామి (తిర్యక్ లేక అనుదైర్ఘ్య తరంగాలు, యానకంలో ఒకే రేఖలో వ్యతిరేక దిశలలో అధ్యారోపణం చెందితే, ఏర్పడు ఫలిత తరంగంను, స్థావర తరంగం అంటారు.

సాగదీసిన తీగలో స్థావర తరంగం ఏర్పడుట :

1. రెండు ‘స్థిర బిందువుల మధ్య ‘l’ పొడవు ఉన్న తండ్రిని దృఢంగా బిగించి, కంపింపచేస్తే, తంత్రి వెంట తిర్యక్ పురోగామి తరంగం ప్రయాణిస్తుంది.
2. తరంగం, దృఢంగా బిగించిన రెండవ చివర నుండి పరావర్తనం చెందును.
3. పతన మరియు పరావర్తన తరంగాలు వ్యతికరణం పల్ల, స్థావర తరంగాలు ఏర్పడతాయి.
4. అస్పందన మరియు ప్రస్పందన స్థానాలతో ఏర్పడిన స్థావర తరంగం పటంలో చూపబడింది.

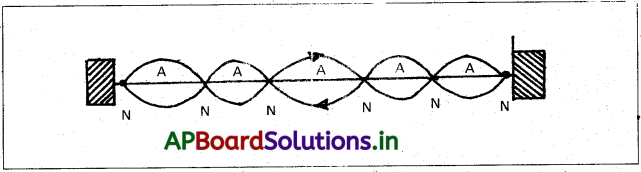
ప్రశ్న 8.
ఒక సాగదీసిన తంత్రిలో ధ్వని వేగాన్ని కొలవడానికి ఒక పద్ధతిని వర్ణించండి.
జవాబు:
ప్రాథమిక రీతిలో సాగదీసిన తంత్రి వెంట, ప్రయాణించు తిర్యక్ తరంగం వేగం v = 2vl, ఇక్కడ υ = పౌనఃపున్యం, l = అనునాదం పొడవు.

సోనోమీటర్ ఉపయోగించి సాగదీసిన తండ్రి (తీగ) వెంట ధ్వని వేగంను నిర్ణయించుట :

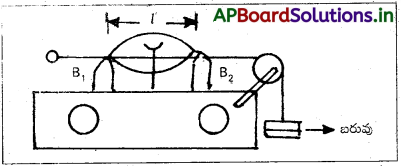
1. సరైన భారంతో తంత్రిని స్థిర తన్యతకు గురి చేస్తారు.
2. పౌనఃపున్యం (v) ఉన్న కంపిస్తున్న శృతి దండం కాడను, సోనోమీటర్ పెట్టె పై ఉంచుతారు
3. రెండు బ్రిడ్జిల మధ్య స్థిర దూరంలో అనునాదం వద్ద B₁ B₂ ల మధ్య పేపర్ రైడర్ పడిపోతుంది.
4. రెండు బ్రిడ్జిల మధ్య అనునాదం పొడవు ‘l’ ను, స్కేలుతో కొలుస్తారు.
5. v మరియు l లు తెల్సుకొని, తరంగవేగం v = 2vl నుపయోగించి కనుగొంటారు.

ప్రశ్న 9.
మూసిన గొట్టంలో స్థిర తరంగాలు ఏర్పడటాన్ని పటం సహాయంతో వివరించండి. ధ్వని జనకం పౌనఃపున్యాన్ని కనుక్కోవడానికి దీన్ని ఏవిధంగా ఉపయోగించవచ్చు?
జవాబు:
మూసిన గొట్టంలో స్థిర తరంగాలు ఏర్పడుట :

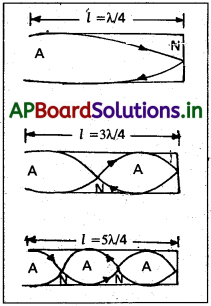
1) మూసిన గొట్టంలో ఒక చివర మూసి, రెండవ చివర తెరిచి ఉండును. తెరిచిన చివర ప్రస్పంద స్థానం, మూసిన చివర అస్పందన స్థానం ఏర్పడును.

2) మూసిన గొట్టంలో, కంపిస్తున్న గాలిస్తంభంలో సాధ్యమగు అనుస్వరాలను యిచ్చే సమీకరణం v_n = \(\frac{(2n + 1)v}{4l}\)
ఇక్కడ n = 0, 1, 2, 3,

3) మొదట కంపన రీతిలో, మూసిన గొట్టంలో గాలిస్తంభ పౌనఃపున్యం ν₁
= \(\frac{υ}{4l}\)(మొదటి అనుస్వరం లేక ప్రాథమిక పౌనఃపున్యం)

4) రెండవ కంపనరీతిలో, మూసిన గొట్టంలో గాలిస్తంభ పౌనః
పున్యము, ν₃ = \(\frac{3υ}{4l}\) (మూడవ అనుస్వరం లేక మొదటి అతిస్వరం)

5) మూడవ కంపనరీతిలో, మూసిన గొట్టంలో గాలిస్తంభ పౌనః
పున్యం, ν₅ = \(\frac{5υ}{4l}\) (ఐదవ అనుస్వరం లేక రెండవ అతిస్వరం)

ధ్వని జనకం పౌనఃపున్యంను నిర్ణయించుట :
1) తెరిచిన గొట్టంపైన, తెలియని పౌనఃపున్య శృతి దండం (v) ను ఉంచుదాము.

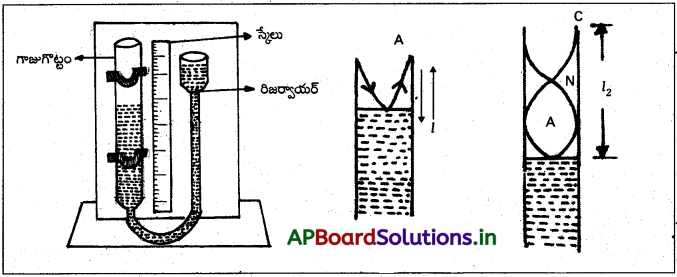
2) రిజర్వాయర్ను నెమ్మదిగా క్రిందికి జరుపుతూ, బిగ్గరగా శబ్దం వినబడే వరకు జరపాలి. మొదటి అనునాదం గాలి స్తంభం పొడవు l₁ ను కొలుద్దాం.

3) రిజర్వాయరు, రెండవ అనునాదం బిగ్గరగా శబ్దం వినబడేటట్లు క్రిందికి జరపాలి. రెండవ అనునాద గాలిస్తంభ పొడవు l₂ ను కొలుద్దాం.

4) 0°C వద్ద తరంగవేగము υ = 331m/s.

5) ν = \(\frac{υ}{2(l_2-l_1)}\) సమీకరణంలో ν, l₁ మరియు l₂ లను ప్రతిక్షేపించి, శృతిదండం తెలియని పౌనఃపున్యం కనుక్కోవచ్చును.

ప్రశ్న 10.
విస్పందనాలు అంటే ఏమిటి? అవి ఎప్పుడు సంభవిస్తాయి? వాటి ఉపయోగాలు ఏమైనా ఉంటే వివరించండి.
జవాబు:
దాదాపు సమాన పౌనఃపున్యం ఉన్న రెండు ధ్వని తరంగాలు, ఒకే దిశలో ప్రయాణిస్తూ, వ్యతికరణం చెందితే, ఫలితంగా ధ్వని తరంగాల తీవ్రత, క్రమకాలవ్యవధులవద్ద గరిష్ఠ ధ్వని మరియు కనిష్ఠ ధ్వని ఏర్పడటాన్ని విస్పందనాలు అంటారు. కంపిస్తున్న వస్తువుల పౌనఃపున్యాలలో స్వల్ప తేడా ఉంటే, విస్పందనాలు ఏర్పడతాయి. విస్పందనాల సంఖ్య.
∆ν = ν₁ ~ ν₂

ప్రాముఖ్యత :

1. మ్యూజికల్ పరికరాలను ట్యూన్ చేయుటకు విస్పందనాలు ఉపయోగిస్తారు.
2. విషవాయువులను గుర్తించుటకు విస్పందనాలు ఉపయోగిస్తారు.

విస్పందనాలతో మ్యూసికల్ పరికరాలను ట్యూన్ చేయుట-వివరణ :
మ్యుజీషియన్స్, మ్యూజిక్ పరికరములను ట్యూన్ చేయుటకు విస్పందనాలను ఉపయోగిస్తారు. ఒక పరికరంను ధ్వనింపచేసి, ప్రామాణిక పౌనఃపున్యంనకు దగ్గరగా ఉంచి విస్పందనాలు అదృశ్యమయ్యే వరకు ట్యూన్ చేస్తారు. అప్పుడు పరికరం ప్రామాణిక పౌనఃపున్యంతో ట్యూన్ చేయబడింది అంటారు.

ప్రశ్న 11.
డాప్లర్ ప్రభావం అంటే ఏమిటి? వివరణాత్మకమయిన ఉదాహరణలు ఇవ్వండి.
జవాబు:
డాప్లర్ ప్రభావం :
ధ్వని జనకం మరియు పరిశీలకులు సాపేక్ష చలనంలో ఉన్నప్పుడు, పరిశీలకుడు వినే దృశ్య పౌనః పున్యంలో మార్పును డాప్లర్ ప్రభావం అంటారు.

ఉదాహరణలు :

1. ఈల వేస్తున్న రైలు ఫ్లాట్ఫాంపై ఉన్న పరిశీలకుని సమీపిస్తూ ఉంటే, పరిశీలకుడు వినే ధ్వని దృశ్య పౌనఃపున్యం పెరుగును. రైలు ఇంజన్ పరిశీలకుని దాటి వెళ్తూ ఉన్నప్పుడు, అతడు వినే ధ్వని దృశ్య పౌనఃపున్యం తగ్గును.
2. ఈల వేస్తున్న అంబులెన్స్ పరిశీలకుని సమీపిస్తూ ఉంటే, అతడు వినే దృశ్య పౌనఃపున్యం పెరుగును. అంబులెన్స్ పరిశీలకుని దాటి వెళ్తూ ఉన్నప్పుడు, అతడు వినే దృశ్య పౌనఃపున్యం తగ్గును.

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 1.
సాగదీసిన తంత్రుల్లో స్థిర తరంగాలు ఏర్పడటాన్ని వివరించండి. దాని నుంచి సాగదీసిన తంత్రుల్లో తిర్యక్ తరంగాల నియమాలను ఉత్పాదించండి.
జవాబు:
ఒక పొడవాటి లోహపు తంత్రి రెండు చివలను దృఢ ఆధారాల మధ్య బిగించి, మధ్య బిందువు వద్ద మీటితే, ఒకే పౌనః పున్యం, ఒకే కంపన పరిమితిగల రెండు పరావర్తన తరంగాల తీగవెంట వ్యతిరేక దిశలలో ప్రయాణిస్తూ కలుస్తాయి. అప్పుడు ఏర్పడు ఫలిత తరంగాలను స్థావర లేక స్థిర తరంగాలు అంటారు.

ఒకే కంపన పరిమితి ‘a’, ఒకే తరంగదైర్ఘ్యం ‘λ’ మరియు ఒకే పౌనఃపున్యం ‘ν’ ఉండి, వ్యతిరేక దిశలలో ప్రయాణించు రెండు పురోగామి తరంగాలు వరుసగా,
y₁ = a sin (kx – ωt) మరియు y₂ = + a sin (kx + ωt)
ఇక్కడ ₁ = 2πν మరియు k = \(\frac{2 \pi}{\lambda}\)
ఫలిత తరంగం, y = y₁ + y₂
y = a sin (kx – ωt) + a sin (kx + ωt)
y = (2a sin kx) cos ωt
2a sin kx = ఫలిత తరంగం కంపన పరిమితి

ఇది ‘kx’ పై ఆధారపడును

ఈ స్థానాలను అస్పందన స్థానాలు అంటారు.

ఈ స్థానాలను ప్రస్పందన స్థానాలు అంటారు.
తంత్రి రెండు భాగాలలో కలిస్తే, దాని రెండవ అనుస్వరం లేక మొదటి అతిస్వరం అంటారు. ఇదేవిధంగా కంపనాలు వరుసలు పటంలో చూపబడినవి.

‘l’ పొడవు ఉన్న ఒక తంత్రి p (ఉచ్చులలో) భాగాలలో కంపిస్తే ప్రతి భాగం పొడవు = \(\frac{l}{p}\)

p = 1 అయితే, దానిని ప్రాధమిక పౌనఃపున్యం (లేక) మొదటి హరాత్మక పౌనఃపున్యం అంటారు.

సాగదీసిన తంత్రి (తీగ) వెంట తిర్యక్ తరంగాల నియమాలు :
కంపన తీగ (తంత్రి) ప్రాథమిక పౌనఃపున్యం v = \(\frac{1}{2 l} \sqrt{\frac{\mathrm{T}}{\mu}}\)

మొదటి నియమము :
తంత్రి తన్యత (1) మరియు రేఖీయ సాంద్రత (u) లు స్థిరంగా ఉన్నప్పుడు, కంపిస్తున్న తంత్రి పౌనఃపున్యం (V), దాని పొడవు (1) కు విలోమానుపాతంలో ఉండును.
∴ v ∝ \(\frac{1}{l}\) ⇒ vl = స్థిరాంకం

రెండవ నియమము :
తంత్రి పొడవు (I) మరియు రేఖీయ సాంద్రత (m) లు స్థిరంగా ఉన్నప్పుడు, కంపిస్తున్న తంత్రి | ప్రాథమిక పౌనఃపున్యం (v), రేఖీయ సాంద్రత వర్గమూలంనకు అనులోమానుపాతంలో ఉండును.
∴ v ∝ √T ⇒ \(\frac{v}{\sqrt{T}}\) = స్థిరాంకం

మూడవ నియమము :
తంత్రి పొడవు (l) మరియు తన్యత (T) లు స్థిరంగా ఉన్నప్పుడు, కంపిస్తున్న తంత్రి ప్రాథమిక పౌనఃపున్యం (υ) తంత్రి రేఖీయ సాంద్రత (m) వర్గమూలమునకు విలోమానుపాతంలో ఉండును.
v ∝ + ⇒ V VI = స్థిరాంకం

ప్రశ్న 2.
తెరచిన గొట్టంలో ఆవృతమైన గాలి స్తంభంలో స్థిర తరంగాలు ఏర్పడటాన్ని వివరించండి. ఉత్పత్తి అయ్యే అనుస్వరాల పౌనఃపున్యాలకు సమీకరణాలు ఉత్పాదించండి.
జవాబు:

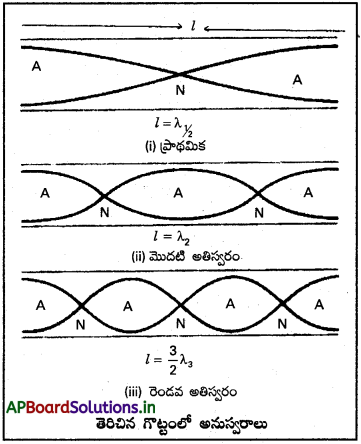
రెండువైపులా తెరిచి ఉన్న గొట్టాలను తెరిచిన గొట్టం అంటారు. తెరిచిన గొట్టంలోనికి, ధ్వని తరంగంను పంపితే, భూమి వల్ల పరావర్తనం చెందును. ఒకే పౌనఃపున్యం ఉన్న పతన మరియు పరావర్తన తరంగాలు వ్యతిరేక దిశలో అధ్యారోపణం చెంది గొట్టంలో స్థిరతరంగాలు ఏర్పడును.

తెరిచిన గొట్టంలో అనుస్వరాలు :
i) తెరిచిన గొట్టంలో స్థిర తరంగం ఏర్పడుటకు, గొట్టం చివరల రెండు ప్రస్పందన స్థానాలు మరియు మధ్యలో ఒక అస్పందన స్థానం ఉండాలి.
అప్పుడు కంపన పొడవు (l)

(ii) రెండవ అనుస్వరం (మొదటి అతిస్వరం) లో మూడు అనుస్వరాలు మరియు రెండు అతిస్వరాలు ఏర్పడును.

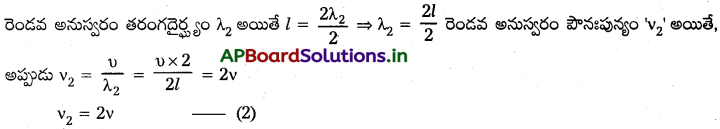
ఇదే విధంగా మూడవ అనుస్వరంలో (రెండవ అతిస్వరంలో) నాల్గు ప్రస్పందన స్థానాలు మరియు మూడు అస్పందన స్థానాలు ఏర్పడును.

తెరిచిన గొట్టంలో అనుస్వరాల పౌనఃపున్యాల నిష్పత్తి ν : ν₁ : ν₂ = 1 : 2 : 3 ………

ప్రశ్న 3.
మూసిన గొట్టాలలో స్థిర తరంగాలు ఏవిధంగా ఏర్పడతాయి ? విభిన్న కంపనరీతులను వివరించండి. వాటి పౌనఃపున్యాలకు సంబంధాలను పొందండి. [AP & TS (Mar. ’15)]
జవాబు:

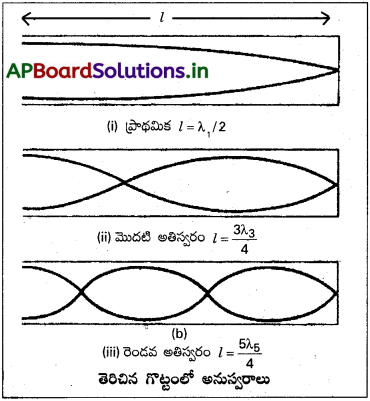
గొట్టం ఒకవైపు మూసి ఉండి, రెండవ వైపు తెరిచి ఉన్న గొట్టంను మూసిన గొట్టం అంటారు. మూసిన గొట్టం తెరిచిన చివర ధ్వని తరంగంను పంపితే, తరంగము మూసిన చివర నుండి పరావర్తనము చెందును. పతన మరియు పరావర్తన తరంగాలు ఒకే పౌనఃపున్యంతో, వ్యతిరేక దిశలలో అధ్యారోపణం చెందుటవల్ల మూసిన గొట్టంలో స్థిర తరంగాలు ఏర్పడును.

మూసిన గొట్టంలో స్థిర తరంగము ఏర్పడుటకు కనీసం మూసిన చివర అస్పందన స్థానం మరియు తెరిచిన చివర ప్రస్పందన స్థానం ఏర్పడాలి. అప్పుడు గొట్టం ప్రాథమిక పౌనః పున్యంతో కంపిస్తుంది. అప్పుడు గొట్టం పొడవు (l) తరంగదైర్ఘ్యంలో నాల్గవ వంతుకు సమానం.
∴ l = \(\frac{\lambda_1}{4}\) ⇒ λ₁ = 4l
‘ν₁‘ ప్రాథమిక పౌనఃపున్యం అయితే,
ν₁ = \(\frac{υ}{\lambda_1}\) ఇక్కడ ‘υ’ గాలిలో ధ్వని వేగం.
ν₁ = \(\frac{υ}{4l}\) = ν ………….. (1)

మూసిన గొట్టంలో తరువాత అనుస్వరంను ఏర్పరుచుటకు గొట్టంలో రెండు అస్పందన మరియు రెండు ప్రస్పందన స్థాయి ఏర్పడాలి. అప్పుడు మూసిన గొట్టము మూడవ అనుస్వరంతో కంపిస్తుంది. అప్పుడు మూసిన గొట్టం పొడవు తరంగదైర్ఘ్యంనకు

ఇదే విధంగా రెండవ అతిస్వరం లేక ఐదవ అనుస్వరం మూడు అస్పందన మరియు మూడు. ప్రస్పందన స్థానాలలో ఏర్పడును. అప్పుడు గొట్టం పొడవు, తరంగదైర్ఘ్యం λ₅ కు \(\frac{5}{4}\) రేట్లు

(1), (2) మరియు (3) సమీకరణాలనుండి అనుస్వర పౌనఃపున్యాల నిష్పత్తి
ν₁ : ν₃ : ν₅ = ν : 3ν : 5ν
ν₁ : ν₃ : ν₅ = 1 : 3 : 5

ప్రశ్న 4.
విస్పందనాలు అంటే ఏమిటి? విస్పందన పౌనఃపున్యానికి ఒక సమాసాన్ని పొందండి. విస్పందనాలు ఎక్కడ, ఎలా ఉపయోగపడతాయి?
జవాబు:
విస్పందనాలు :
సమీప పౌనఃపున్యంగల రెండు ధ్వని తరంగాలు ఒకే దిశలో ప్రయాణిస్తూ, వ్యతికరణం చెందితే, క్రమ కాలవ్యవధుల వద్ద, ఫలిత ధ్వని తీవ్రత వృద్ధి మరియు క్షీణత ఉండు దృగ్విషయంను విస్పందనాలు అంటారు.

ఒకే దిశలో అధ్యారోపణం చెందు ధ్వని తరంగాల పౌనఃపున్యాలు ν₁ మరియు ν₂ అయితే, ఒక సెకనులో వినే విస్పందనాల సంఖ్య ∆ν = ν₁ – ν₂.

స్పష్టంగా వినటానికి సెకనుకు వినే గరిష్ఠ విస్పందనాల సంఖ్య 10.

విస్పందన పౌనఃపున్యంనకు సమానము:

1. దాదాపు సమాన పౌనఃపున్యాలు, ఒకే కంపన పరిమితిగల రెండు ధ్వని తరంగాలను భావిద్దాం.
2. రెండు తరంగాల పౌనఃపున్యాలు ν₁ మరియు ν₂. ν₁ > ν₂ అనుకుందాము.
3. విస్పందన ఆవర్తన కాలం T సెకనులు
4. మొదటి తరంగం T సెకనులలో చేయు కంపనాల సంఖ్య = ν₁T
   [∵ 1 సెకనులో కంపనాల సంఖ్య = ν]
   [T సెకనులో కంపనాల సంఖ్య = νt]
5. రెండవ తరంగం T సెకనులలో చేయు కంపనాల సంఖ్య = ν₂ T
6. T కాలవ్యవధిలో రెండవ తరంగంకన్నా మొదటి తరంగం ఒక పూర్తి భ్రమణంను అధికంగా కలిగి ఉండును.
7. కావున, ν₁T – ν₂T = 1 లేక ν₁ – ν₂ = \(\frac{1}{T}\)
8. ఒక సెకనులో ఏర్పడే విస్పందనాల సంఖ్య = \(\frac{1}{T}\) ఇక్కడ T విస్పందన ఆవర్తన కాలం.
9. ∵ విస్పందన పౌనఃపున్యం = \(\frac{1}{T}\) = ν₁ – ν₂ = ∆ν
10. విస్పందన పౌనఃపున్యం, రెండు తరంగాల పౌనఃపున్యాల భేదంనకు సమానము.

విస్పందనాల ప్రాయోగిక అనువర్తనాలు:

1. శృతిదండం తెలియని పౌనఃపున్యంను కనుగొనవచ్చును.
2. సంగీత పరికరములను ట్యూన్ చేయుటకు ఉపయోగిస్తారు.
3. సినిమాటోగ్రఫిలోని ప్రత్యేక ప్రభావం ఉత్పత్తిచేయుటకు ఉపయోగిస్తారు.
4. గనులలో విషవాయువులను గుర్తించుటకు ఉపయోగిస్తారు.

ప్రశ్న 5.
డాప్లర్ ప్రభావం అంటే ఏమిటి? నిశ్చల స్థితిలో ఒక పరిశీలకుని దృష్ట్యా జనకం చలనంలో ఉన్నప్పుడు వినపడే ధ్వని దృశ్య పౌనఃపున్యానికి ఒక సమాసాన్ని పొందండి. [T.S (Mar. ’17) AP (Mar.’16) (Mar. ’14)]
జవాబు:
డాప్లర్ ప్రభావము :
ధ్వని జనకము మరియు పరిశీలకుడు సాపేక్ష చలనంలో ఉన్నప్పుడు, పరిశీలకుడు విని దృశ్య పౌనఃపున్యంలోని మార్పును, డాప్లర్ ప్రభావము అంటారు.

ఈల వేస్తున్న రైలు ఇంజన్, ప్లాట్ఫాంపై ఉన్న పరిశీలకుని సమీపిస్తూ ఉంటే, పరిశీలకుడు వినే దృశ్య పౌనఃపున్యం పెరుగును. రైలు ఇంజన్ పరిశీలకుని దాటితే, పరిశీలకుడు వినే దృశ్య పౌనఃపున్యం తగ్గును.

ధ్వనిజనకం చలనంలో మరియు పరిశీలకుడు నిశ్చలంగా ఉన్నప్పుడు, దృశ్య పౌనఃపున్యంనకు సమాసము :

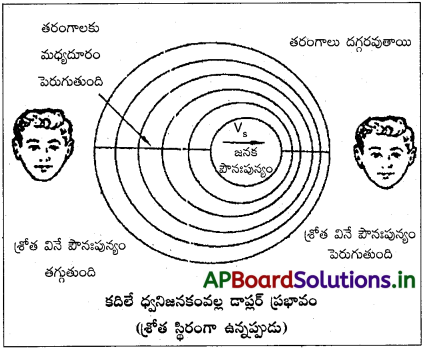
S = ధ్వని జనకం
O = పరిశీలకుడు

ధ్వని జనకం, ‘S’ నిశ్చలంగా ఉన్న పరిశీలకుని వైపు ‘υ_s‘ వేగంతో చలిస్తుందని భావిద్దాం.
ఆవర్తన కాలం T లో జనకం ప్రయాణించు దూరం = υ_s T
వరుస సంపీడనాలు మరియు విరళీకరణాలు పరిశీలకునికి దగ్గరగా గీయబడినవి.
∴ దృశ్య తరంగదైర్ఘ్యం, λ’ = λ – υ_sT.

∴ దృశ్య పౌనఃపున్యం, నిజ పౌనఃపున్యం కన్నా ఎక్కువ.

ఇదేవిధంగా, ధ్వని జనకం, నిశ్చలంగా ఉన్న పరిశీలకుని నుండి దూరం చలిస్తుంటే, పరిశీలకుడు వినే దృశ్య పౌనఃపున్యం . పరిశీలకుడు వినే దృశ్య పౌనఃపున్యం, నిజ పౌనఃపున్యం కన్నా తక్కువ.

ప్రశ్న 6.
డాప్లర్ విస్థాపనం అంటే ఏమిటి? నిశ్చల స్థితిలో ఒక జనకం దృష్ట్యా పరిశీలకుడు చలనంలో ఉన్నప్పుడు వినపడే ధ్వని దృశ్య పౌనఃపున్యానికి ఒక సమాసాన్ని పొందండి.
జవాబు:
డాప్లర్ విస్థాపనం :
సాపేక్ష చలనంలో ధ్వని జనకము, పరిశీలకుని దగ్గరకు వచ్చినపుడు, దృశ్య పౌనఃపున్యం, నిజ పౌనఃపున్యం కన్నా ఎక్కువ. ధ్వని జనకము, పరిశీలకునికి దూరంగా ఉన్నప్పుడు, దృశ్య పౌనఃపున్యం నిజ పౌనఃపున్యంకన్నా తక్కువ. దృశ్య మరియు నిజ పౌనఃపున్యాల భేదంను డాప్లర్ విస్థాపనం అంటారు.

చలన పరిశీలకుడు వినే దృశ్య పౌనఃపున్యంనకు సమానము:

సందర్భం (1) :
పరిశీలకుడు జనకంవైపు చలిస్తూ ఉన్నప్పుడు : పరిశీలకుడు ‘O’, v_o వేగంతో నిశ్చలంగా ఉన్న జనకం ‘S’ వైపు పటములో చూపినట్లు చలిస్తుందని భావిద్దాం. అందువల్ల పరిశీలకుడు ప్రతి సెకనులో గ్రహించే తరంగాల సంఖ్య ఎక్కువ.
ఒక సెకనులో పరిశీలకుడు ప్రయాణించు దూరం = υ₀
పరిశీలకుడు గ్రహించే అదనపు తరంగాల సంఖ్య = \(\frac{υ_0}{\lambda}\)

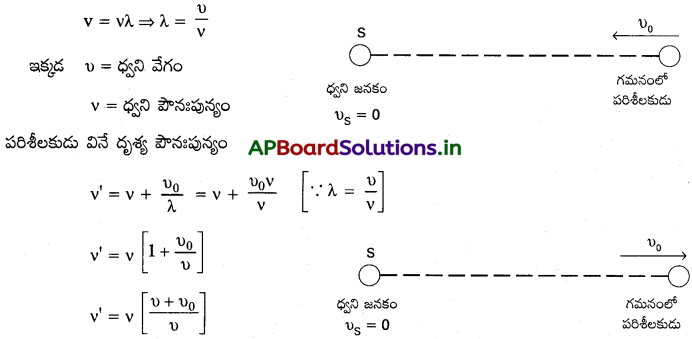
∴ దృశ్య పౌనఃపున్యం, నిజ పౌనఃపున్యం కన్నా ఎక్కువ.

సందర్భం (2) :
పరిశీలకుడు నిశ్చలంగా ఉన్న జనకం నుండి దూరంగా చలిస్తూ ఉన్నప్పుడు
పరిశీలకుడు, నిశ్చలంగా ఉన్న జనకం నుండి దూరంగా చలిస్తూ ఉన్నప్పుడు, పరిశీలకుడు కోల్పోయే తరంగాల సంఖ్య \(\frac{ν_0}{\lambda}\)

లెక్కలు Problems

ప్రశ్న 1.
0.6m పొడవు గల ఒక సాగదీసిన తంత్రి ప్రాథమిక కంపనరీతిలో 30Hzల పౌనఃపున్యంతో కంపిస్తుందని పరిశీలించారు. తంత్రి 0.05 kg/m ల రేఖీయ సాంద్రత కలిగి ఉంటే (a) ఆ తంత్రిలో తిర్యక్ తరంగాల ప్రసార వేగాన్ని (b) తండ్రిలో తర్వతుడు కనుక్కోండి.
సాధన:
v = 30Hz; l = 0.6 m ; µ = 0.05 kg m^-1
υ = ?; T = ?
a) υ = 2vl = 2 × 30 × 0.6 = 36 m/s
b) T = vu = 36 × 36 × 0.05 = 64.8 N

ప్రశ్న 2.
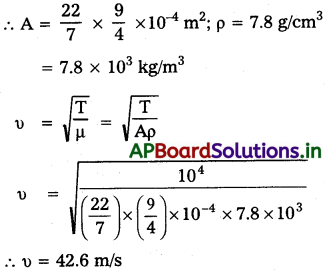
3cm వ్యాసం గల ఒక ఉక్కు కేబుల్ను 10kN తన్యతకు లోబడి ఉంచారు. ఉక్కు సాంద్రత 7.8 g/cm³. ఆ కేబుల్ వెంట ఎంత వడితో తిర్యక్ తరంగాలు ప్రయాణిస్తాయి?
సాధన:
T = 10 kN = 10⁴

ప్రశ్న 3.
ఒక సాగదీసిన తంత్రి వెంబడి ప్రయాణిస్తున్న రెండు పురోగామి తరంగాలు y = 0.07 sinπ (12x- 500t), y₂ = 0.07 sinπ (12x + 500t) అస్పందనాలు, ప్రస్పందనలను ఏర్పరుస్తున్నాయి. (a) అస్పందనలు (b) విస్పందనల వద్ద స్థానభ్రంశం ఎంత ? స్థిర తరంగం తరంగదైర్ఘ్యం ఏమిటి ?
సాధన:
A₁ = 0.07; A₂ = 0.07; K = 12π
a) అస్పందన స్థానాల వద్ద, స్థానభ్రంశము,
y = A₁ – A₂ = 0.07 0.07 = 0.

b) ప్రస్పందన స్థానాల వద్ద, స్థానభ్రంశము,
y = A₁ + A₂ = 0.07 + 0.07 = 0.14 m

c) తరంగదైర్ఘ్యం λ = \(\frac{2 \pi}{K}=\frac{2 \pi}{12 \pi}\) = 0.16m

ప్రశ్న 4.
ఒక తంత్రి 0.4m పొడవు, 0.16g ద్రవ్యరాశి కలిగి ఉంది. తంత్రిలో తన్యత 70N అయితే, దాన్ని మీటినప్పుడు అది ఉత్పత్తిచేసే మూడు అత్యల్ప పౌనః పున్యాలు ఏమిటి?
సాధన:
l = 0.4 m; M = 0.16g = 0.16 × 10^-3 kg;

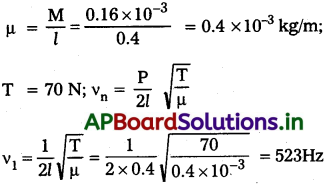
v₂ = 2v₁ = 2 × 523 = 1046 Hz
v₃ = 3v₁ = 3 × 523 = 1569 Hz

ప్రశ్న 5.
ఒక లోహపు కడ్డీని దాని మధ్య బిందువు వద్ద బిగించి నప్పుడు దాని ప్రాథమిక పౌనఃపున్యంలో, 4kHz పౌనః పున్యంగల అనుదైర్ఘ్య తరంగాలతో అనునాదం చేస్తుంది. ఆ బిగింపును ఒక చివరికి జరిపితే దాని ప్రాధమిక అనునాద పౌనఃపున్యం ఎంత అవుతుంది?
సాధన:
l పొడవు ఉన్న ఒక లోహపు కడ్డీ మధ్యలో బిగింపు ఉంచి ప్రాధమిక రీతిలో కంపింపచేస్తే, మధ్యలో ఒక అస్పందన స్థానం, కడ్డీ రెండు స్వేచ్ఛా చివరల ప్రస్పందన స్థానంబు ఏర్పడును.
l = \(\frac{\lambda}{2}\) ⇒ λ = 2l

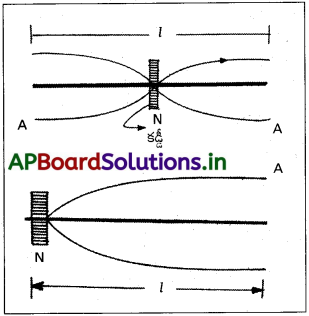
ప్రాథమిక’ రీతిలో కడ్డీ పౌనఃపున్యం = తరంగ పౌనః పున్యం = 4 kHz.

ప్రశ్న 6.
70 cm పొడవు గల ఒక మూసిన ఆర్గాన్ పైపును ధ్వనింపచేశారు. ధ్వనివేగం 331 m/s అయితే గాలి స్తంభపు కంపన ప్రాథమిక పౌనఃపున్యం ఎంత? [A.P (Mar. ’17)]
సాధన:

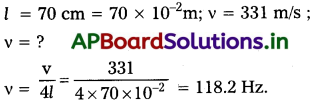
ప్రశ్న 7.
ఒక నిట్టనిలువు గొట్టాన్ని నీటితో నిల్చి ఉండేటట్లు ఉంచారు. దానిలో నీటి మట్టాన్ని సర్దుబాటు చేయవచ్చు. ఆ గొట్టంపై నుంచి 320 Hz పౌనఃపున్యం గల ధ్వని తరంగాలను పంపించారు. రెండు వరుస నీటిమట్టాలు 20cm, 73 cm వద్ద స్థిర తరంగాలు ఏర్పడితే, ఆ గొట్టపు గాలిలో ధ్వని తరంగాల వడి ఎంత?
సాధన:
v = 320 Hz; l₁ = 20cm = 20 × 10^-2 m
l₂ = 73 cm = 73 × 10^-2m; υ = ?
υ = 2v (l₂ – l₁)
= 2 × 320 (73 × 10^-2 – 20 × 10^-2)
∴ υ = 339 m/s

ప్రశ్న 8.
65cm, 70cm పొడవులు గల రెండు ఆర్గాన్ పైపులను ఒకేసారి ధ్వనింపచేస్తే, ఆ రెండు పైపుల ప్రాథమిక పౌనఃపున్యాల మధ్య సెకనుకు ఎన్ని విస్పందనాలు ఉత్పత్తి అవుతాయి? (ధ్వని వేగం = 330 m/s).
సాధన:
l₁ = 65 cm = 0.65 m
l₂ = 70 cm = 0.7 m
υ = 330 m/s
ఒక సెకనులో విస్పందనాల సంఖ్య ∆ν = ν₁ – ν₂

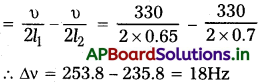
ప్రశ్న 9.
ఒక రైలు ఒక లెవెల్ క్రాసింగ్ను సమీపిస్తున్నప్పుడు, దాటేప్పుడు ఈల వేస్తుంది. ఆ క్రాసింగ్ వద్ద ఉన్న ఒక పరిశీలకుడు ఆ రైలు సమీపిస్తున్నప్పుడు 219 Hz పౌనః పున్యంగా, అది వెళ్ళేటప్పుడు 184 Hz పౌనఃపున్యంగా కొలిచాడు. ధ్వని వడిని 340 m/s గా తీసుకొంటే ఆ రైలు వడిని, దాని ఈల పౌనఃపున్యాన్ని కనుక్కోండి. [T.S (Mar.’17)]
సాధన:
ఈల వేస్తున్న ఒక రైలు క్రాసింగ్ వద్ద ఉన్న పరిశీలకుని సమీపిస్తూ ఉంటే,

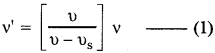
ఈల వేస్తున్న ఒక రైలు క్రాసింగ్ వద్ద ఉన్న పరిశీలకుని నుండి దాటి వెళ్ళేటప్పుడు,

ఇక్కడ v’. = 219 Hz; v” = 184Hz;
υ = 340 m/s

ప్రశ్న 10.
60 kmph, 70 kmph వడులతో రెండు ట్రక్కులు వ్యతిరేకదిశలలో ఎదురవుతూ సమీపిస్తున్నాయి. మొదటి ట్రక్కు చోదకుడు (driver) 400Hz పౌనఃపున్యంతో హారన్ ధ్వని చేస్తున్నాడు. రెండవ ట్రక్కు చోదకుడు ఎంత పౌనఃపున్యాన్ని వింటాడు? (ధ్వని వేగం 330 m/s). ఆ రెండు ట్రక్కులు ఒకదానిని మరొకటి దాటిన తరవాత రెండవ ట్రక్కు చోదకుడు ఎంత పౌనః పున్యాన్ని వింటాడు?
సాధన:

రెండు ట్రక్కులు ఒకదానికొకటి సమీపిస్తూ ఉంటే, రెండవ ట్రక్కు చోదకుడు వినే పౌనఃపున్యం

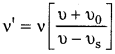
రెండు ట్రక్కులు ఒకదానికొకటి దాటిన తరువాత,
రెండవ ట్రక్కు చోదకుడు పౌనఃపున్యం

అభ్యాసాలు Textual Exercises

ప్రశ్న 1.
2.50 kg ద్రవ్యరాశి గల ఒక తంత్రి 200 N తన్యతకు లోబడి ఉన్నది. సాగదీసిన తంత్రి పొడవు 20.0 m. ఆ తంత్రి ఒక చివర తిర్యక్ కుదుపును కలిగిస్తే, ఆ అలజడి మరొక చివరకు చేరడానికి ఎంత సమయం పడుతుంది?
సాధన:
M = 2.50 kg, T = 200N, T = 20.0M

ప్రశ్న 2.
300m ఎత్తుగల ఒక గోపురం పైభాగం నుంచి ఒక రాయిని జారవిడిస్తే అది దాని పీఠం దగ్గర ఉన్న కొలనులోని నీటిలో పడింది. గాలిలో ధ్వని వడి 340 ms^-1 గా ఇస్తే నీటిలో పడినప్పుడు వచ్చే శబ్దం పైభాగాన ఎప్పుడు వినిపిస్తుంది? (g = 9.8m s^-2)
సాధన:
h = 300m, g= 9.8 m/s²), υ = 340 m/s.
నీటి మడుగు ఉపరితలంపై రాయి తాకుటకు పట్టు కాలం t₁ అయితే,

ధ్వని గోపురం పైకి చేరుటకు పట్టుకాలం
t₂ = \(\frac{h}{ν}=\frac{300}{400}\) = 0.88s
రాయి నీటిని తాకిన తరువాత శబ్దం వినుటకు పట్టు కాలం = t₁ + t₂ = 7.82 + 0.88 = 8.70s.

ప్రశ్న 3.
ఒక ఉక్కు తీగ 12.0 m పొడవు, 2.10 kg ల ద్రవ్యరాశి కలిగి ఉంది. ఆ తీగపై తిర్యక్ తరంగ వడి, 20° C వద్ద గల పొడి గాలిలో ధ్వని వడి 343 m s^-1 కు సమానం అయితే ఆ తీగలో తన్యత ఎంత ఉండాలి?
సాధన:
l = 12.0m, µ = 2.10 kg, T = ?
v = 343 m/s
ప్రమాణ పొడవుకు ద్రవ్యరాశి µ = \(\frac{m}{l}=\frac{2.10}{12.0}\) = 0.175 kg/m
v = \(\sqrt{\frac{\mathrm{T}}{\mu}}\)
T = υ².µ = (343)² × 0.175 2.06 × 10⁴ N.

ప్రశ్న 4.
v = \(\sqrt{\frac{\gamma \mathbf{P}}{\rho}}\) ఫార్ములాను ఉపయోగించి ఈ క్రింది వాటిని వివరించండి.
a) గాలిలో ధ్వని వడి పీడనం మీద ఆధారపడదు.
b) గాలిలో ధ్వని వడి ఉష్ణోగ్రతతో పెరుగుతుంది.
c) గాలిలో ధ్వని వడి తేమతో పెరుగుతుంది.
సాధన:
పీడన ప్రభావము:
వాయువులలో ధ్వని వడి υ = \(\sqrt{\frac{\gamma \mathbf{P}}{\rho}}\)
స్థిర ఉష్ణోగ్రతవద్ద, PV = స్థిరాంకము
P\(\frac{\mathrm{m}}{\rho}\) = స్థిరాంకము ⇒ \(\frac{\mathrm{P}}{\rho}\) = స్థిరాంకము
పీడనం పెరిగిన, P కూడా పెరుగును. కావున గాలిలో ధ్వని వడి, పీడనంపై ఆధారపడదు.

ఉష్ణోగ్రత ప్రభావము :

STP వద్ద నీటిఆవిరి సాంద్రత, పొడిగాలి సాంద్రత కన్నా తక్కువ. గాలిలో తేమ, గాలిసాంద్రత తగ్గించును. ధ్వనివడి సాంద్రత మార్గమూలంనకు విలోమానుపాతంలో ఉండును. ధ్వని పొడిగాలిలో కన్నా తేమ గాలిలో ఎక్కువ వడితో ప్రయాణించును. కావున ధ్వని వడి υ ∝ తేమ.

ప్రశ్న 5.
ఏకమితీయంలో ప్రయాణించే తరంగాన్ని y = f(x, t) అనే ఒక ప్రమేయంతో సూచిస్తారని మీకు తెలుసు. ఇక్కడ x, t లు x – υt లేదా x + υt ల సంయోగంగా కనిపిస్తుంది. అంటే, y = f(x ± υt). దీని విపర్యయం సత్యమా? y యొక్క క్రింది ప్రమేయాలు ప్రయాణ తరంగాలను సూచిస్తాయో లేదో పరీక్షించండి:
a) (x – υt)²
b) log[(x + υt) / x₀]
e) 1/(x + υt)
సాధన:
కాదు, విలోమము సత్యం కాదు. X మరియు t విలువలకు ప్రయాణించు తరంగంను సూచించుటకు తరంగ ప్రమేయం కావాలి. తరంగ ప్రమేయం నిర్ణీత విలువ కలిగి ఉండును.

ఇచ్చిన ప్రమేయంలలో, ప్రమేయంను ఏది కూడా సంతృప్తపరచదు.
∴ ప్రయాణించు తరంగంను ఏది కూడా సూచించదు.

ప్రశ్న 6.
ఒక గబ్బిలం 1000 kHz పౌనఃపున్యం గల అతిధ్వనిని గాలిలో విడుదల చేస్తుంది. ఆ ధ్వని ఒక నీటి ఉపరితలాన్ని తాకితే, (a) పరావర్తిత ధ్వని (b) ప్రసారిత ధ్వనుల తరంగదైర్ఘ్యం ఎంత? గాలిలో ధ్వని వడి 340 m s^-1, నీటిలో ధ్వని వడి 1486 m s^-1.
సాధన:
υ = 100KHz = 10₅ Hz, υ_a = 340 m/s,
υ_w = 1486 ms^-1

ప్రశ్న 7.
ఒక వైద్యశాలలో అతిధ్వని క్రమ వీక్షణాన్ని (ultrasonic scanner) కణజాలకంలోని కణతుల స్థానాన్ని గుర్తించ దానికి ఉపయోగిస్తున్నారు. ఆ కణజాలకంలో ధ్వని వడి 1.7 km s^-1 అయితే దానిలో ధ్వని తరంగదైర్ఘ్యం ఎంత? ఆ క్రమ వీక్షణ లేదా స్కానర్ పనిచేసే (ప్రచాలనమయ్యే) పౌనఃపున్యం 4.2 MHz.
సాధన:
v = 1.7 Kms^-1 = 1700 ms^-1
v = 4.2 MHz = 4.2 × 10⁶Hz

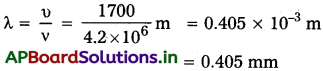
ప్రశ్న 8.
ఒక తంత్రిపై ఒక తిర్యక్ హరాత్మక తరంగాన్ని ఈ విధంగా వర్ణించారు.
y(x, t) = 3.0 sin (36 t + 0.018 x + π/4)
ఇక్కడ x, y cm లో; t సెకను (S) లలో ఉన్నాయి. x ధన దిశ ఎడమ నుంచి కుడివైపుకు ఉంది.
a) ఇది ప్రయాణించే తరంగమా లేదా స్థిర తరంగమా? ఇది ప్రయాణించేది అయితే దాని ప్రసార వడి, ప్రసార దిశ ఏమిటి?
b) దాని కంపనపరిమితి, పౌనఃపున్యం ఎంత?
c) మూల బిందువు వద్ద దాని తొలిదశ ఏమిటి?
d) ఆ తరంగంలో రెండు వరస శృంగాల మధ్య కనిష్ఠ దూరం ఎంత?
సాధన:
ఇచ్చిన సమీకరణంను, కుడి నుండి ఎడమ వైపుకు υ వడితో ప్రయాణించు ‘r’ కంపన పరిమితిగల సమతల పురోగామి తరంగంతో పోలిస్తే,

a) ఇచ్చిన సమీకరణం, కుడి నుండి ఎడమకు ప్రయాణించు తిర్యక్ హరాత్మక తరంగంను సూచిస్తుంది.
b) ఇచ్చిన సమీకరణంను ఇంకొక విధంగా వ్రాస్తే,

తరంగం రెండు వరుస శృంగాల మధ్య
కనిష్ట దూరము = తరంగదైర్ఘ్యం

ప్రశ్న 9.
అభ్యాసం 8 లో వివరించిన తరంగానికి, స్థానభ్రంశం (y), కాలం (t) గ్రాఫ్ను x = 0.2, 4 cm లకు గీయండి. ఈ గ్రాఫ్ ఆకారాలు ఏమిటి? ప్రయాణ తరంగంలోని డోలన చలనం, ఏ రీతిలో ఒక బిందువు నుంచి మరొక బిందువుకు కంపనపరిమితి, పౌనఃపున్యం లేదా దశలు విభేదిస్తాయి?
సాధన:
తిర్యక్ హరాత్మక తరంగము y(x, t) = 3.0

వేర్వేరు t విలువలకు, (i) ను ఉపయోగించి yని గణించి, పట్టికలో పొందుపరచుదాము.

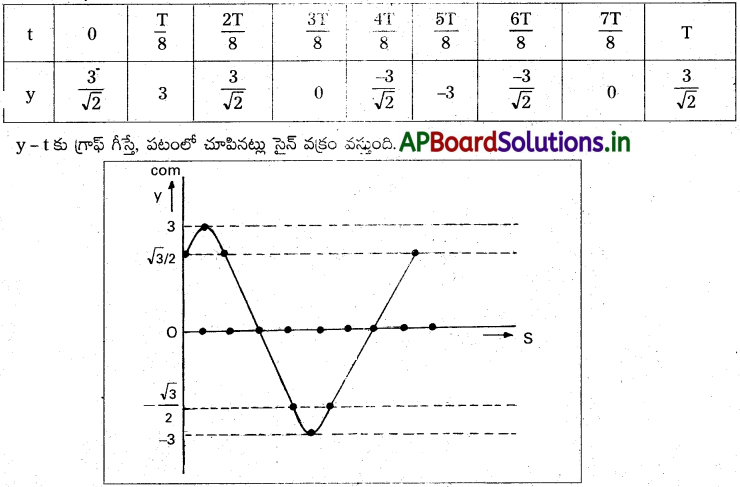
x = 2 cm మరియు x = 4 cm కు ఇదేవిధము అయిన గ్రాఫ్లు వస్తాయి. తరంగ ప్రయాణంలో డోలన చలనం ఒక స్థానం నుండి మరియొక స్థానంనకు దశ పడములలో వేర్వేరుగా ఉండును. కంపన పరిమితి మరియు పౌనఃపున్యాలు మూడు సందర్భాలలో డోలన చలనం స్థిరంగా ఉండును.

ప్రశ్న 10.
ప్రయాణించే హరాత్మక తరంగానికి y(x, t) = 2.0 cos 2 π (10 – 0.0080 x + 0.35) ఇక్కడ x, y cm లో, t సెకను (S) లో ఉన్నాయి. క్రింద ఇచ్చిన దూరంతో వేరుచేసిన డోలన చలనం చేసే రెండు బిందువుల మధ్య దశా భేదాన్ని గణించండి.
a) 4 m
b) 0.5 m
c) λ/2
d) 3λ/4
సాధన:
ఇచ్చిన సమీకరణంను ఇంకొక విధంగా వ్రాస్తే
y = 2.0 cos[2л(10t – 0.0080x) + 2л × 0.35]

ప్రశ్న 11.
ఒక తంత్రి (రెండు చివరలు బిగించి ఉన్న) తిర్యక్ స్దాన భ్రంశాన్ని y(x, t) = 0.06 sin (\(\frac{2 \pi}{3}\) x) cos (120 πt) తో సూచిస్తున్నారు. ఇక్కడ x, y m లో t సెకన్ (s) ఉన్నాయి. ఆ తంత్రి పొడవు 1.5 m, ద్రవ్యరాశి 3.0 × 10^-2 kg.
క్రింది వాటికి జవాబు ఇవ్వండి.
a) ఆ ప్రమేయం ఒక ప్రయాణ తరంగాన్ని లేదా ఒక స్థిర తరంగాన్ని సూచిస్తుందా?
b) ఆ తరంగాన్ని వ్యతిరేక దిశలలో ప్రయాణించే రెండు తరంగాల అధ్యారోపణంగా అర్థం చేసుకోండి. ప్రతీ తరంగపు తరంగదైర్ఘ్యం, పౌనఃపున్యం వడి ఎంత?
c) ఆ తంత్రిలో తన్యతను కనుక్కోండి.
సాధన:
ఇచ్చిన సమీకరణం
y(x, t) = 0.06 sin\(\frac{2 \pi}{3}\) x cos 120 πt ………… (i)

a) సమీకరణం x మరియు tలతో హరాత్మక ప్రమేయం కలిగి, స్థావర తరంగంన తెల్పును.
b) తరంగము
y₁ = r sin \(\frac{2 \pi}{\lambda}\) (υt + x)
ధన X-అక్షం దిశలో ప్రయాణిస్తూ, పరావర్తన తరంగం
y₂ = -r sin \(\frac{2 \pi}{\lambda}\) (υt + x) తో వ్యతిరేక దిశలో అధ్యారోపణం చెందితే, స్థావర తరంగం

రెండు తరంగాలు ఒకే తరంగదైర్ఘ్యం, ఒకే పౌనఃపున్యం మరియు ఒకే వడిని కల్గి ఉండును.
c) తిర్యక్ తరంగ వడి

ప్రశ్న 12.
i) అభ్యాసం 11లో ఇచ్చిన ఒక తంత్రిపై ఉన్న తరంగానికి, ఆ తంత్రిపై ఉన్న అన్ని బిందువులు ఒకే (a) కంపనపరిమితి, (b) దశ, (c) పౌనఃపున్యంతో డోలనాలు చేస్తాయా? మీ జవాబులను వివరించండి. (ii) ఒక చివర నుంచి 0.375 m దూరంలో ఉన్న ఒక బిందువు కంపనపరిమితి ఎంత?
సాధన:
తీగపై అన్ని స్థానాల వద్ద
i) అస్పందన స్థానాల వద్ద (పౌనఃపున్యం సున్న) తప్ప మిగిలిన అన్ని స్థానాల వద్ద ఒకే పౌనఃపున్య విలువను కలిగి ఉండును.
ii) అస్పందన స్థానాల వద్ద తప్పు ఉచ్చులో ఎక్కడైనా ఒకేఒక దశ కలిగి ఉండును. వేర్వేరు స్థానాల వద్ద కంపన పరిమితులు వేర్వేరుగా ఉండును.

ప్రశ్న 13.
ఒక స్థితిస్థాపక తరంగ స్థానభ్రంశాన్ని (తిర్యక్ లేదా అనుదైర్ఘ్య) సూచించడానికి x, tలలో కొన్ని ప్రమేయాలు కింద ఇవ్వడమైంది. వీటిలో ఏవి (i) ఒక ప్రయాణించే తరంగాన్ని, (ii) ఒక స్థిర తరంగాన్ని లేదా (iii) ఏదీ కాని దాన్ని సూచిస్తాయి?
a) y = 2 cos (3x) sin (10t)
b) y = \(2 \sqrt{x-v t}\)
c) y = 3 sin (5x-0.5t) + 4 cos (5x-0.5t)
d) y = cos x sin t + cos 2x sin 2t
సాధన:
a) సమీకరణంలో x మరియు t లు వేరుగా ఉన్న హరాత్మక ప్రమేయంలతో స్థావర తరంగంను సూచించును.

b) ఏ రకమైన తరంగంను సూచించదు.

c) ఇది పురోగామి లేక హరాత్మక తరంగంను సూచిస్తుంది.

d) ఈ సమీకరణం రెండు ప్రమేయాల మొత్తం ఒక్కొక్కటి స్థావర తరంగంను సూచిస్తుంది. ఇది స్థావర తరంగాల అధ్యారోపణంను సూచిస్తుంది.

ప్రశ్న 14.
రెండు దృఢ ఆధారాల మధ్య సాగదీసిన తీగ 45 Hz పౌనఃపున్యంతో దాని ప్రాథమిక రీతిలో కంపిస్తుంది. ఆ తీగ ద్రవ్యరాశి 3.5 × 10^-2 kg రేఖీయ ద్రవ్యరాశి సాంద్రత 4.0 × 10^-2 kg m^-1. (a) ఆ తీగపై తిర్యక్ తరంగ వడి, (b) ఆ తీగలో తన్యత ఎంత?
సాధన:
v = 45Hz, u = 3.5 × 10^-2 kg
ద్రవ్యరాశి/పొడవు = u = 4.0 × 10^-2 kg/m^-1

ప్రశ్న 15.
ఒక మీటరు పొడవు గల ఒక గొట్టం ఒక చివర తెరవబడి, మరొక చివర కదలగలిగే పిస్టన్ (ముషలకం)తో ఒక స్థిరమైన పౌనఃపున్యం గల జనకం (340 Hz పౌనః పున్యం గల శృతిదండం) తో గొట్టం పొడవు 25.5 cm లేదా 79.3 cm ఉన్నప్పుడు అనునాదంలో ఉన్నది. ప్రయోగ ఉష్ణోగ్రత వద్ద గాలిలో ధ్వని వడిని అంచనా వేయండి. అంచు ప్రభావాలను (edge effects) ఉపేక్షించవచ్చు.
సాధన:
గొట్టంలో ముషలకం ఒక చివర ఉంటే, మూసిన గొట్టం వలె ఉండి బేసి అనుస్వరాలను ఉత్పత్తి చేయును.

గొట్టం ప్రాథమిక పౌనఃపున్యంతో అనునాదంలో ఉండి మూడవ అనుస్వరం 79.3 సెం.మీ ఘమారు 25.5 సెం.మీ.కు 3 రెట్లు ఉండును.

ప్రాథమిక అనుస్వరం వద్ద \(\frac{\lambda}{4}\) = l₁ = 25.5
λ = 4 × 25.5 = 102 cm = 1.02 m
గాలిలో ధ్వని వడి
v = vλ = 340 × 1.02
= 346.8 m/s

ప్రశ్న 16.
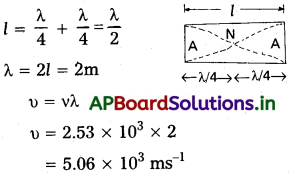
100 cm పొడవు ఉన్న ఒక ఉక్కు కడ్డీని దాని మధ్య భాగంలో బిగించారు. ఆ కడ్డీ అనుదైర్ఘ్య కంపనాల ప్రాథమిక పౌనఃపున్యాన్ని 2.53 kHz లుగా ఇస్తే ఉక్కులో ధ్వని వడి ఎంత?
సాధన:
l = 100 cm = Im, v = 2.53 KHz
= 2.53 × 10³ Hz

కడ్డీని మధ్యలో బిగిస్తే, కడ్డీ ప్రాథమిక కంపన పద్ధతిలో, మధ్యలో అస్పందన మరియు చివరల స్పందన స్థానాలు ఏర్పడును.
పటం నుండి

ప్రశ్న 17.
20 cm పొడవు గల గొట్టం ఒక చివర మూసి ఉన్నది. 430 Hz ల ఒక జనకంతో ఉత్తేజపరిస్తే, ఆ గొట్టపు ఏ అనుస్వరరీతి అనునాదంలో ఉంటుంది? ఆ గొట్టం రెండు చివరలు తెరచి ఉంటే అదే జనకంతో అనునాదంలో ఉండగలదా?
(గాలిలో ధ్వని వడి 340 m s^-1).
సాధన:
l = 20 cm = 0.2m, v_n = 430 Hz
υ = 340m/s
0.2m, vn = 430 Hz,
మూసిన గొట్టం nవ సాధారణ కంపన స్థితిలో పౌనఃపున్యం

n ఇంటిజిర్ను కల్గి ఉంటే, తెరిచిన గొట్టం జనకంతో అనునాదంలో ఉండును.

ప్రశ్న 18.
A, B అనే రెండు సితార్ తంత్రులతో ‘గ’ స్వరాన్ని వాయిస్తున్నప్పుడు కాస్తంత శృతి తప్పి 6 Hz పౌనః పున్యంగల విస్పందనాలను ఉత్పత్తి చేసాయి. A తంత్రిలో కాస్తంత తన్యతను తగ్గిస్తే విస్పందన పౌనఃపున్యం 3 Hz లకు తగ్గిందని కనుక్కొన్నారు. A అసలు పౌనఃపున్యం 324 Hz అయితే, B పౌనఃపున్యం ఎంత?
సాధన:
A సితార్ తంత్రి యదార్థ పౌనఃపున్యం n_a మరియు B సితార్ తంత్రి యదార్ధ పౌనఃపున్యం n_b.
1 సెకన్ ఏర్పడు విస్పందనాల సంఖ్య = 6
n_b = n_a ± 6 = 324 ± 6 = 330 లేక 318Hz.
∴ Aలో తన్యత తగ్గిస్తే పౌనఃపున్యం తగ్గును.
(∴ n ∝ √T).
ఒక సెకనుకు విస్పందనాల సంఖ్య 3 కు తగ్గితే,
B పౌనఃపున్యం = 324 – 6
= 318Hz.

ప్రశ్న 19.
ఎందుకు (లేదా ఎలా) వివరించండి :
a) ధ్వని తరంగంలో స్థానభ్రంశ అస్పందనమే పీడన ప్రస్పందనం, స్థానభ్రంశం ప్రస్పందనమే పీడన అస్పందనం.
b) ఏవిధమైన ‘కళ్ళు’ లేకుండానే గబ్బిలాలు అడ్డంకుల దూరాలను, దిశలను, స్వభావాన్ని, పరిమాణాలను రూఢీపరచుకోగలవు –
c) ఒక వయోలిన్ స్వరం, సితార్ స్వరం ఒకే పౌనః పున్యాన్ని కలిగి ఉండవచ్చు. అయినప్పటికీ మనం ఆ రెండు స్వరాల మధ్య తేడా తెలుసుకోగలం.
d) ఘనపదార్థాలు అనుదైర్ఘ్య, తిర్యక్ తరంగాలు రెండింటిని ప్రసారం చేయగలవు. కాని వాయువులలో అనుదైర్ఘ్య తరంగాలు మాత్రమే ప్రసరిస్తాయి.
e) ఒక విక్షేపక (dispersive) యానకంలో స్పందన ఆకారం ప్రసార సమయంలో విరూపణ చెందుతుంది.
సాధన:
a) అస్పందన (N) స్థానం వద్ద డోలన కంపన పరిమితి శూన్యం (మరియు పీడనం గరిష్ఠం). ప్రస్పందన (A) స్థానంవద్ద డోలన కంపన పరిమితి గరిష్ఠం (పీడనం కనిష్ఠం). ఈ అస్పందన, ప్రస్పందనాలు పీడన అస్పందన మరియు ప్రస్పందనాలతో ఏకీభవించవు. నిర్వచనాల నుండి స్పష్టంగా N, పీడన ప్రస్పందన మరియు A, పీడన అస్పందన స్థానాలతో ఏకీభవించును.

b) గబ్బిలాలు ఎక్కువ పౌనఃపున్యమున్న అతిధ్వనులను ఉద్గారం చేయును. ఈ తరంగాలు అవే మార్గంలో. వస్తువుల నుండి పరావర్తనం చెందును. అవి దూరం, దిశ, పరిమాణం మరియు వస్తువు స్వభావం గూర్చిన ఉపాయంను ఇస్తుంది.

c) వయోలిన్ మరియు సితార్ ల స్వర పౌనఃపున్యం సమానం, అప్పుడు అతిస్వరాలు ఏర్పడును. వాని ప్రతిచర్య బలాలు వేరుగా ఉండుట వలన రెండు స్వరాలను వేరుపరచవచ్చును.

d) ఘనపదార్థాలు, ఘనపరిమాణం స్థితిస్థాపకత మరియు వియోటన స్థితిస్థాపక కలిగి ఉండును. కాని వాయువు ఘనపరిమాణ స్థితిస్థాపకతను మాత్రమే కల్గి ఉండును.

e) ధ్వని సంకేతం, వేర్వేరు తరంగదైర్ఘ్యాలగల తరంగాల సంయోగం వేర్వేరు తరంగదైర్ఘ్యాలగల తరంగాలు యానకంలో వేర్వేరు వడులతో వేర్వేరుగ ప్రయాణించును. కావున ధ్వని తరంగ సంకేతము విరూపణ చెందును.

ప్రశ్న 20.
ఒక రైల్వే స్టేషన్లో బయటి సిగ్నల్ వద్ద నిలబడిన రైలు నిలకడ గాలిలో 100 Hz పౌనఃపున్యంతో ఈల వేసింది. i) ఆ రైలు (a) 10ms^-1 వడితో ప్లాట్ఫామ్న సమీపిస్తున్నప్పుడు, b) 10 m s^-1 వడితో ప్లాట్ఫామ్ నుంచి దూరంగా పోతున్నప్పుడు, ప్లాట్ఫామ్ మీద పరిశీలకుడు వినే ఈల పౌనఃపున్యం ఏమిటి? ii) ప్రతి సందర్భంలో ధ్వని వడి ఎంత?’ నిలకడ గాలిలో ధ్వని వడిని 340 m s^-1 గా తీసుకోవచ్చు?
సాధన:
v = 400Hz, υ = 340m/s^-1

a) ప్లాట్ఫాం దగ్గరకు రైలు సమీపిస్తుండగా ఉంటే,
υ = 10m/s

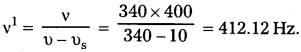
b) రైలు ప్లాట్ఫాంను వదులుతూ ఉన్నప్పుడు,
υ_s = 10m/s

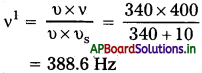
ii) ప్రతి సందర్భంలో ధ్వని సమానం = 340m/s

ప్రశ్న 21.
ఒక రైల్వే స్టేషన్-ప్రాంగణ స్థలం (station-yard)లో నిల్చున్న రైలు నిలకడ గాలిలో 400 Hz ల పౌనః పున్యంతో ఈల వేసింది. 10ms^-1 వడితో స్థలం నుంచి ప్రాంగణం దిశలో పవనం వీయడం మొదలయితే ఆ ప్రాంగణ ప్లాట్ఫామ్ మీద నిల్చొన్న పరిశీలకుడు వినే ధ్వని పౌనఃపున్యం, తరంగదైర్ఘ్యం, వడి ఎంత? ఈ పరిస్థితి గాలి నిలకడగా ఉండి, పరిశీలకుడు స్థలంవైపు 10 m s^-1 వడితో పరిగెత్తే సందర్భంతో కచ్చితంగా సర్వసమంగా ఉంటుందా? నిలకడ గాలిలో ధ్వని వడిని 340 m s^-1 గా తీసుకోవచ్చు.
సాధన:
v = 400 Hz, υ_m = 10ms^-1, υ = 340m/s^-1
గాలి ధ్వని ప్రయాణ దిశలో చలిస్తే, ధ్వని తుల్యవడి
= υ + υ_m = 340 + 10 = 350m/s^-1
జనకం మరియు పరిశీలకుడు విరామ స్థితిలో ఉంటే, పౌనఃపున్యం మారదు.
i.e. v = 400 Hz.

జనకం విరామ స్థితివద్ద ఉంటే, తరంగదైర్ఘ్యం మారదు.
i.e, λ¹ = λ = 0.875M.
ధ్వని వడి = υ + υ_m = 340 + 0 = 340 m/s
పై రెండు సందర్భాలలో పరిస్థితులు పూర్తిగా వేరుగా, ఉండును.

అదనపు అభ్యాసాలు Additional Exercises

ప్రశ్న 22.
ఒక తంత్రిపై ప్రయాణించే ఒక హరాత్మక తరంగాన్ని ఈ విధంగా వర్ణిస్తే,
y(x, t)= 7.5 sin (0.0050x + 12t + π/4)
a) x = 1 cm, t = 1 s వద్ద ఉన్న ఒక బిందువు డోలన స్థానభ్రంశం, వేగం ఎంత? ఈ వేగం తరంగ ప్రసార వేగానికి సమానంగా ఉంటుందా?
b) t = 2s,11s ల వద్ద x = 1 cm బిందువులాగా స్థానభ్రంశాలు, వేగాలు కలిగి ఉన్న బిందువుల స్థానాలను గుర్తించండి.
సాధన:
a) హరాత్మక తరంగము y(x, t)

(1) నుండి, y(1, 1) = 7.5 sin (732.55°)
= 7.5 sin (720 + 12.55°)
7.5 sin12.55° = 7.5 × 0.2173 = 1.63 cm

= 90 cos (732.55°)
= 90 cos(72) + 12.55°)
υ = 90 cos (12.55°)
= 90 × 0.9765
= 87.89 cm/s.
ఇచ్చిన సమీకరణంను ప్రమాణ రూపంతో పోల్చగా

x = 1 cm t = 1 sec వద్ద వేగం, తరంగ ప్రసార వేగంనకు సమానం కాదు.

b) x = 1cm నుండి అన్ని స్థానాల దూరాలు ±λ, ± 2λ, ± 3λ లు ఒకే తిర్యక్ స్థానభ్రంశము మరియు వేగం కలిగియుండును. λ = 12.56 m అయిన t = 2sec, 5 sec మరియు 11 sec ల వద్ద x = 10m నుండి అన్ని స్థానాల దూరాలు ±12.6m, ±25.2m ,±37.8m

ప్రశ్న 23.
ఒక సన్నని ధ్వని స్పందనను (ఉదాహరణకు, ఒక చిన్న పిప్ (pip) ఈల) ఒక యానకం ద్వారా పంపారు. (a) ఆ స్పందనకు ఒక నిర్ణీత (i) పౌనఃపున్యం, (ii) తరంగదైర్ఘ్యం, (iii) ప్రసార వడి ఉంటాయా? (b) స్పందన రేటు ప్రతి 20 s తరవాత 1 ఉంటే (అంటే ఆ ఈలను ప్రతి 20 సెకనుల తరవాత రెండవ స్పందన వెలువడేటట్లు అతిస్వల్ప సెకండు వరకు ఊదితే) ఆ ఈల ఏర్పరచే స్వర పౌనఃపున్యం 1/20 లేదా 0.05 Hz లకు సమానం అవుతుందా?
సాధన:
a) ఒక చిన్న పిప్ ఈలను ఊదితే, నిర్దిష్ట తరంగదైర్ఘ్యంను మరియు నిర్దిష్ట పౌనఃపున్యం కలిగి ఉండవు. ప్రసార వడిని స్థిరంగా ఉంచితే, అది గాలిలో ధ్వని వడినకు సమానము.

b) కాదు. ఈల ఏర్పరచు ధ్వని పౌనఃపున్యం = 1/20 = 0.05 Hz. ఒక చిన్న పిప్ ఈల వల్ల పునరుత్పాదన పౌనఃపున్యం = 0.05 Hz

ప్రశ్న 24.
రేఖీయ ద్రవ్యరాశి సాంద్రత 8.0 × 10^-3 kg m^-1 ఉన్న ఒక పొడవైన తంత్రి ఒక చివర విద్యుత్ నడిచే 256 Hz పౌనఃపున్యం గల ఒక శృతిదండానికి కలిపారు. రెండవ చివరను కప్పి మీదగా పోయేటట్లు చేసి 90 kg ద్రవ్యరాశి గల ఒక పళ్ళానికి కట్టారు. కప్పీ చివర వస్తున్న మొత్తం శక్తిని శోషించుకోవడంవల్ల ఆ చివర పరావర్తనం చెందే తరంగ కంపనపరిమితి ఉపేక్షించే విధంగా ఉంటుంది. t = 0 వద్ద, ఆ తంత్రి ఎడమ చివర (దండం చివర) ×=0, శూన్య తిర్యక్ స్థానభ్రంశం (y = 0) కలిగి ఉండి, ధన y-దిశలో చలిస్తుంది. ఆ తరంగ కంపనపరిమితి 5.0 cm. ఆ తంత్రిపై రంగాన్ని వర్ణించే తిర్యక్ స్థానభ్రంశం y ని x, tల ప్రమేయంగా వ్రాయండి.
సాధన:
m = 8.0 × 10^-3 kgm^-1, v = 256 Hz,
T= 90kg = 90 × 9.8 = 882N.
తరంగ వేగము, = 5.0m = 0.05m.
తీగవెంట ప్రసారించు తిర్యక్ తరంగ వేగము

తరంగము ధన x-అక్ష దిశలో ప్రసారమయితే, తరంగ సమీకరణము
y(x, t) = r sin (ωt – kx) = 0.05 sin (1.61 × 10³t – 4.84x)
ఇక్కడ x, y లు మీటర్లు మరియు t secలలో ఉండును.

ప్రశ్న 25.
ఒక జలాంతర్గామిలో అమర్చిన ఒక సోనార్ (SONAR) వ్యవస్థ 40.0 kHz పౌనఃపున్యం వద్ద పనిచేస్తుంది. ఆ సోనార్ వైపు ఒక శత్రు జలాంతర్గామి 360 km h^-1వడితో చలిస్తుంది. ఆ శత్రు జలాంతర్గామి పరావర్తనం `చేసే ధ్వని పౌనఃపున్యం ఎంత? నీటిలో ధ్వని వడిని 1450 m s^-1 గా తీసుకోండి.
సాధన:
సోనార్ పౌనఃపున్యం,
v = 40kHz = 40 × 10³ Hz.
పరిశీలకుని/శత్రు జలాంతర్గామి వడి
υ_L = 360 km/h 360 ×\(\frac{5}{18}\) ms^-1 = 100ms^-1

నీటిలో ధ్వని తరంగ వడి υ = 1450 ms^-1.

నిశ్చల స్థితిలో ఉన్న జనకంవైపు పరిశీలకుడు చలిస్తున్నప్పుడు, శత్రు జలాంతర్గమి గ్రహించే దృశ్య పౌనఃపున్యము

ఈ పౌనఃపున్యంను శత్రు జలాంతర్గామి (జనకం) పరావర్తనం చేయును. దీనిని సోనార్ పరిశీలించును. ఈ సందర్భంలో

ప్రశ్న 26.
భూకంపాలు భూమిలోపల ధ్వని తరంగాలను ఉత్పత్తి చేస్తాయి. ఒక వాయువు లాగా కాకుండా భూమిలో తిర్యక్ (S), అనుదైర్ఘ్య (P) ధ్వని తరంగాలు రెండూ ప్రసరిస్తాయి. విలక్షణంగా S తరంగ వడి సుమారు 4.0 km s^-1. P తరంగానికి అది 8.0 km s^-1. ఒక భూకంపం నుంచి ఒక భూకంపలేఖిని (seismograph P, S తరంగాలను నమోదు చేస్తుంది. మొదటి P తరంగం మొదటి S తరంగం కంటే 4 నిమిషాలు ముందుగా చేరుతుంది. ఆ తరంగాలు సరళరేఖ మార్గంలో ప్రయాణిస్తాయని ఊహిస్తే, ఆ భూకంపం ఎంత దూరంలో సంభవించినట్లు?
సాధన:
S తరంగాలు మరియు తరంగాల వేగాలు υ₁ మరియు υ₂. సెస్మోగ్రాఫ్ను చేరుటకు వాటికి పట్టుకాలాలు t₁ మరియు t₂. సెస్మోగ్రాఫ్ నుండి భూకంపం ఏర్పడిన దూరం 1.
అప్పుడు l = υ₁t₁ = υ₂t₂ ……… (i)
υ₁ = 4 kms^-1 మరియు υ₂ = 8 kms^-1
∴ 4t₁ = 8t₂ లేక t₁ = 2t₂ ……… (ii)
t₁ – t₂ = = 4min = 240s.

(ii) నుపయోగించి 2t₂ – t₂ = 240s, t₂ = 240s
(i) నుండి l = υ₁t₁ = 4 × 480 1920 km.
కావున భూకంపం, భూకంపలేఖిని నుండి 1920 km వద్ద ఏర్పడును.

ప్రశ్న 27.
ఒక గబ్బిలం తన రెక్కలను రెపరెపలాడిస్తూ అతిధ్వని శబ్దాల ద్వారా మార్గాన్ని నిర్దేశించుకొంటూ ఒక గుహలో అటు ఇటు తిరుగుతుంది. గబ్బిలం వెలువరిచే ధ్వని పౌనఃపున్యాన్ని 40 kHz గా ఊహించండి. ఆ గబ్బిలం గాలిలో ధ్వని వడికి 0.03 రెట్ల వడితో చలిస్తున్నప్పుడు, ఎదురుగా ఉన్న ఒక పెద్ద గోడ ఉపరితలాన్ని దూరం నుంచి అకస్మాత్తుగా ఎదుర్కొన్నది. ఆ గోడ నుంచి పరావర్తనాన్ని ఆ గబ్బిలం ఎంత పౌనఃపున్యంతో వింటుంది?
సాధన:
గబ్బిలం వెలువరించు ధ్వని పౌనఃపున్యం, v = 40kHz.
గబ్బిళం వడి υ_s = 0.03υ, ఇక్కడ υ ధ్వని గోడను తాకు ధ్వని దృశ్య పౌనఃపున్యం,

ఈ పౌనఃపున్యంను గోడ పరావర్తనం చెందించును మరియు గబ్బిలం గోడవైపు చలించేటప్పుడు గ్రహించును. అందువలన υ_s = 0.

సాధించిన సమస్యలు Textual Examples

ప్రశ్న 1.
క్రింద ఇచ్చిన తరంగ చలనానికి కొన్ని ఉదాహరణలు. ప్రతి సందర్భంలో తరంగ చలనం తిర్యక్, అనుదైర్ఘ్య లేదా ఆ రెండింటి కలయికలలో ఏది అవుతుందో తెలపండి.
a) ఒక అనుదైర్ఘ్య స్ప్రింగ్ ఒక చివరను పక్కలకు స్థానభ్రంశం చెందిస్తే, ఆ స్ప్రింగ్లో ఉత్పన్నమయ్యే నొక్కు (kink) చలనం.
b) ద్రవంతో నిండిన స్తూపం ముషలకం (piston) స్థానాన్ని ముందుకు, వెనకకు కదిలిస్తే స్తూపంలో ఉత్పన్నమయ్యే తరంగాలు.
c) మోటారు పడవను నీటిలో నడిపినప్పుడు ఉత్పన్నమయ్యే తరంగాలు
d) కంపించే క్వార్డ్ స్పటికంపల్ల ఉత్పన్నమయ్యే గాలి లోని అతిధ్వని తరంగాలు.
సాధన:
a) తిర్యక్, అనుదైర్ఘ్య
b) అనుదైర్ఘ్య
c) తిర్యక్, అనుదైర్ఘ్య
d) అనుదైర్ఘ్య

ప్రశ్న 2.
ఒక తీగ వెంబడి ప్రయాణించే ఒక తరంగాన్ని ఈ విధంగా వర్ణించారు. y(x, t) = 0.005 sin (80.00 x 3.0t), ఇందులో సంఖ్యా స్థిరాంకాలు SI ప్రమాణాలలో ఉన్నాయి (0.005 m, 80.0 rad m^-1, 3.00 rad s^-1) ఆ తరంగం (a) కంపనపరిమితి, (b) తరంగదైర్ఘ్యం, (c) ఆవర్తన కాలం పౌనఃపున్యాలను గణించండి. x = 30.0 cm దూరం వద్ద, కాలం t = 20 s వద్ద ఉన్నప్పుడు కూడా ఆ తరంగ స్థానభ్రంశం y ని గణించండి.
సాధన:
ఇచ్చిన స్థానభ్రంశ సమీకరణాన్ని y(x, t) = a sin (kx – ωt + Φ) తో పోల్చగా y(x, t) = a sin (kx – ωt) దీని నుంచి,
a) ఆ తరంగ కంపనపరిమితి 0.005m – 5 mm.
b) కోణీయ తరంగ సంఖ్య k, కోణీయ పౌనఃపున్యం ω లు k = 80.0 m^-1, ω = 3.0 s^-1 అని తెలుస్తాయి.
λ = \(\frac{2 \pi}{k}\) లేదా k = k = \(\frac{2 \pi}{\lambda}\)

అప్పుడు మనం సమీకరణం (1.6) ద్వారా తరంగ దైర్ఘ్యం λ ని k కి సంబంధపరుస్తాం.

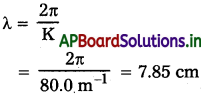
c) ఇప్పుడు T ని ω పరంగా రాస్తే,

x = 30.0 cm, కాలం t= 20s వద్ద స్థానభ్రంశం
y = (0.005 m) sin (80.0 × 0.3 – 3.0 × 20)
= (0.005 m) sin (-36 + 12π)
= (0.005 m) sin (1.699)
= (0.005 m) sin (97°) ≅ 5 mm

ప్రశ్న 3.
0.72 m పొడవు గల ఒక ఉక్కు తీగ 5.0 × 10^-3 kgల ద్రవ్యరాశి కలిగి ఉంది. ఆ తీగ 60 N తన్యతకు లోనయితే తీగపై తిర్యక్ తరంగ వడి ఎంత?
సాధన:
తీగ ఏకాంక పొడవుకు ద్రవ్యరాశి

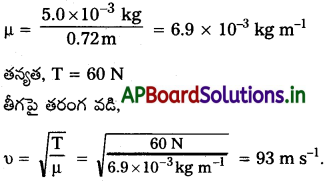
ప్రశ్న 4.
ప్రామాణిక ఉష్ణోగ్రత, పీడనాల వద్ద గాలిలో ధ్వని వడిని అంచనావేయండి. 1 mole గాలి ద్రవ్యరాశి 29.0 × 103 kg.
సాధన:
ప్రామాణిక ఉష్ణోగ్రత, పీడనాలు (STP) వద్ద 1 mole ఏ వాయువైనా 22.4 లీటర్లు ఆక్రమిస్తుంది. అందువల్ల STP వద్ద గాలి సాంద్రత :

ρ₀ (ఒక మోల్ గాలి ద్రవ్యరాశి) / (STP వద్ద ఒక మోల్ గాలి ఘనపరిమాణం).

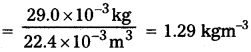
యానకంలో ధ్వని వడికి న్యూటన్ ఫార్ములా ప్రకారం, STP వద్ద గాలిలో పొందగలిగే ధ్వని వడి,

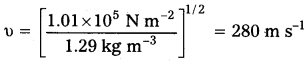
ప్రశ్న 5.
30.0cm పొడవు గల ఒక గొట్టం రెండు చివరలు తెరచి ఉన్నాయి. ఆ గొట్టం ఏ అనుస్వరం 1.1 kHz జనకంతో అనునాదంలో ఉంటుంది ? ఆ గొట్టం ఒక చివరను మూసివేస్తే అదే జనకంతో అనునాదాన్ని గమనించవచ్చా? గాలిలో ధ్వని వడిని 330 ms^-1 గా తీసుకోండి.
సాధన:
మొదటి అనుస్వర పౌనఃపున్యం,
v₁ = \(\frac{υ}{\lambda_1}=\frac{υ}{2L}\) (తెరచిన గొట్టం)

ఇక్కడ L అనేది గొట్టం పొడవు. దాని nవ అనుస్వర పౌనఃపున్యం:
v_n = \(\frac{nυ}{2L}\), n = 1, 2, 3, ……………. (తెరచిన గొట్టం)
తెరచిన గొట్టపు మొదటి కొన్ని కంపనరీతులు పటంలో చూపడమైంది.
L = 30.0 cm. υ = 330 m s^-1

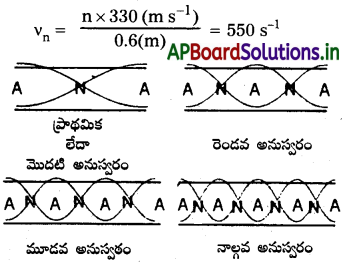
(a) తెరచిన గొట్టంలో స్థావర తరంగాలు, మొదటి నాలుగు అనుస్వరాలు :
స్పష్టంగా 1.1 kHz పౌనః పున్యం గల జనకానికి, గాలి స్తంభం υ₂ వద్ద అనునాదం చెందగలదు. అంటే రెండడ అనుస్వరం వద్ద, ఇప్పుడు ఆ గొట్టం ఒక చివర మూసివేస్తే ప్రాథమిక పౌనఃపున్యం.
ν₁ = \(\frac{υ}{\lambda_1}=\frac{υ}{4L}\) (ఒక చివర మూసిన గొట్టం)
బేసి సంఖ్య అనుస్వరాలు మాత్రమే, కింద చూపినట్లు, ఉంటాయి.

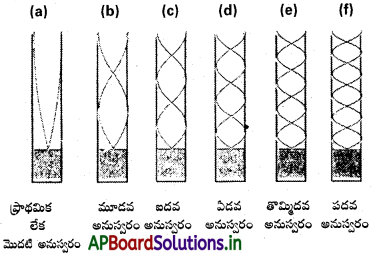
(2) ఒక చివర తెరచిన మరొక చివర మూసిన ఒక గాలి స్థంభపు సామాన్య కంపనరీతులు. కేవలం బేసి అనుస్వరాలు మాత్రమే సాధ్యమవుతున్నట్లు తెలుస్తుంది.
ν₃ = \(\frac{3υ}{4L}\), ν₅ = \(\frac{5υ}{4L}\)

L = 30 cm, υ = 3300 m s^-1కు, చివర మూసిన గొట్టపు ప్రాథమిక పౌనఃపున్యం 275 Hz దాని నాల్గవ అనుస్వరానికి జనక పౌనఃపున్యం అనురూపంగా
ఉంటుంది.

ప్రశ్న 6.
A, B అనే రెండు సితార్ తంత్రులు ‘ద’ స్వరాన్ని వాయించేటప్పుడు వాటి కృతిలో కొద్ది తేడా వల్ల అవి 5 Hz పౌనఃపున్యం గల విస్పందనాలను ఉత్పత్తి చేస్తున్నాయి. B తీగ తన్యతను కొద్దిగా పెంచితే విస్పందనాల పౌనఃపున్యం 3 Hz కు తగ్గినట్లు కనుక్కొన్నారు. A పౌనఃపున్యం 427 Hz అయితే B అసలు పౌనఃపున్యం ఎంత?
సాధన:
తీగ తన్యతలో పెరుగుదల దాని పౌనఃపున్యాన్ని పెంచుతుంది. B అసలు పౌనఃపున్యం (ν_B), A(ν_A), కంటే ఎక్కువగా ఉంటే, ν_B లోని మరింత పెరుగుదల విస్పందన పౌనః పున్యాన్ని పెంచుతుంది. కాని విస్పందన పౌనఃపున్యం తగినట్లు కనుక్కొన్నారు. దీని ద్వారా తెలిసేదేమిటంటే
ν_B < ν_A, ν_A – ν_B = 5 Hz, ν_A = 427 Hz కాబట్టి
ν_B = 422 Hz.

ప్రశ్న 7.
ఒక రాకెట్ 200 m s^-1 వడితో ఒక స్థిర లక్ష్యం వైపు చలిస్తున్నది. చలిస్తున్నప్పుడు అది 1000 Hz పౌనఃపున్యం గల ఒక తరంగాన్ని ఉద్గారిస్తుంది. లక్ష్యాన్ని చేరే ధ్వనిలోని కొంత భాగం ఒక ప్రతిధ్వనిలాగా రాకెట్ వైపుకు వెనుకకు పరావర్తనం చెందుతుంది. 1) లక్ష్యం గుర్తించిన ధ్వని పౌనఃపున్యాన్ని, 2) రాకెట్ గుర్తించిన ప్రతిధ్వని పౌనః పున్యాన్ని లెక్కించండి. [AP (Mar.’16)]
సాధన:
1) పరిశీలకుడు నిశ్చల స్థితిలో ఉన్నాడు. జనకం 200 msā వడితో చలిస్తుంది. ఇది ధ్వని వేగం 330 ms^-1 తో పోల్చదగినదిగా ఉన్నందువల్ల
(\(\frac{1+υ_s}{υ}\))^-1 సమీకరణం υ = υ₀ ని ఉపయోగించాలి. కాని ఉజ్జాయింపు ని కాదు. జనకం స్థిరంగా
సమీకరణం ν₀ (1 – \(\frac{υ_s}{υ}\))ఉన్న లక్ష్యాన్ని సమీపిస్తున్నందువల్ల υ₀ = 0, ν_sని బదులు -υ_s ని తీసుకోవాలి. అందువల్ల,
υ₀ = 0 (\(\frac{1+υ_s}{υ}\))^-1
(దీనిలో ν₀ జనకం ఉద్గారించే పౌనఃపున్యం).
ν = 1000 Hz × [1 – 200 m s^-1/330 m s^-1]^-1 ≅ 2540 Hz

2) ఇప్పుడు లక్ష్యం జనకం (ఎందుకంటే ఇది ప్రతిధ్వని జనకం), రాకెట్ శోధకం ఇప్పుడు పరిశీలకుడు (ఎందుకంటే అది ప్రతిధ్వనిని గుర్తిస్తుంది). అందువల్ల, υ₀ = 0, υ₀ ఒక ధనాత్మక విలువను కలిగి ఉంటుంది. జనకం (లక్ష్యం) ఉద్గారించే ధ్వని పౌనః పున్యం ν లక్ష్యం అడ్డగించే ధ్వని పౌనఃపున్యం అవుతుంది. అది ν₀ మాత్రం కాదు. అందువల్ల, రాకెట్ నమోదు చేసే పౌనఃపున్యం