AP Inter 2nd Year Physics Study Material Chapter 11 విద్యుదయస్కాంత తరంగాలు

Andhra Pradesh BIEAP AP Inter 2nd Year Physics Study Material 11th Lesson విద్యుదయస్కాంత తరంగాలు Textbook Questions and Answers.

AP Inter 2nd Year Physics Study Material 11th Lesson విద్యుదయస్కాంత తరంగాలు

అతిస్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
X – కిరణాల సగటు తరంగదైర్ఘ్యం ఎంత?
జవాబు:
X – కిరణాల తరంగదైర్ఘ్య వ్యాప్తి 10^-8 m (10nm) నుండి 10^-13 m (10^-4 nm)
X – కిరణాల సగటు తరంగదైర్ఘ్యము = \(\frac{10+0.0001}{2}\) = 5.00005 nm

ప్రశ్న 2.
పరారుణ కిరణాల ఒక ఉపయోగాన్ని తెలపండి. [AP. Mar. 16]
జవాబు:

1. భూమిని వేడిగా ఉంచడంలో పరారుణ కిరణాలు ప్రముఖ పాత్ర వహిస్తాయి.
2. ఫిజియోథెరపీలో పరారుణ దీపాలను ఉపయోగిస్తారు.
3. భూ ఉపగ్రహాల ఉనికిని గుర్తించడానికి పరారుణ శోధకాలను వాడతారు.
4. మంచు, పొగ మొదలగు పరిస్థితులలో ఫొటోలు తీయడానికి వీటిని ఉపయోగిస్తారు.

ప్రశ్న 3.
విద్యుదయస్కాంత వికిరణ తరంగదైర్ఘ్యాన్ని రెట్టింపు చేస్తే ఫోటాన్ శక్తి ఎలా మారుతుంది?
జవాబు:

ప్రశ్న 4.
విద్యుదయస్కాంత తరంగాల ఉత్పత్తి సూత్రం ఏమిటి?
జవాబు:
అంతరాళం మరియు కాలంలో అయస్కాంత క్షేత్రం మరియు విద్యుత్ క్షేత్రం మారి ఆవేశము త్వరణము చెందితే, విద్యుదయస్కాంత తరంగాలు జనిస్తాయి.

ప్రశ్న 5.
శూన్యంలో పరారుణ కిరణాల, అతినీలలోహిత కిరణాల వడుల నిష్పత్తి ఎంత?
జవాబు:
శూన్యంలో పరారుణ కిరణాలు మరియు అతినీలలోహిత కిరణాల వేగాల నిష్పత్తి 1 : 1 శూన్యంలో విద్యుదయస్కాంత తరంగాలు అన్నీ ఒకే వేగం 3 × 10⁸ మి/సె కలిగి ఉంటాయి.

ప్రశ్న 6.
స్వేచ్ఛాంతరాళంలో ఒక విద్యుదయస్కాంత తరంగానికి, విద్యుత్, అయస్కాంత క్షేత్రాల గోలన పరిమితుల మధ్య సంబంధం ఏమిటి?
జవాబు:
E₀ = CB₀
ఇక్కడ E₀ = విద్యుత్ క్షేత్రం యొక్క కంపన పరిమితి
B₀ = అయస్కాంత క్షేత్రం యొక్క కంపన పరిమితి
C = కాంతి వేగం:

ప్రశ్న 7.
సూక్ష్మ (మైక్రో) తరంగాల అనువర్తనాలేమిటి? [TS. Mar.’15]
జవాబు:

1. మైక్రో తరంగాలను రాడార్లలో ఉపయోగిస్తారు.
2. మైక్రో తరంగాలను వంట చేయుటకు ఉపయోగిస్తారు.
3. చలనంలో ఉన్న వాహనం యొక్క వేగాన్ని అంచనా వేయడానికి మైక్రో తరంగాలలో రాడార్లలో వాడతారు.

ప్రశ్న 8.
రాడార్లలో సూక్ష్మ తరంగాలను ఉపయోగించడానికి కారణం ఏమిటి? [Mar. ’14]
జవాబు:
మైక్రో- తరంగాలు స్వల్ప తరంగదైర్ఘ్యాన్ని కలిగి ఉంటాయి. అందువలన ఒక నిర్దిష్ట దిశలో కిరణ సంకేతం వలె ప్రసారం చేయవచ్చు. ఇవి ప్రయాణించు మార్గంలో అడ్డు యొక్క అంచు వద్ద వంగవు.

ప్రశ్న 9.
పరారుణ కిరణాల రెండు ఉపయోగాలను ఇవ్వండి. [TS. Mar.’17]
జవాబు:

1. డీహైడ్రేటెడ్ పండ్ల తయారీలో పరారుణ కిరణాలను వాడతారు.
2. గోడలపై పురాతన కాలంనాటి రాతలను గుర్తించడానికి వీటిని వాడతారు.
3. గ్రహం వేడిగా ఉండుటకు హరిత గృహప్రభావాన్ని కలిగించుటకు వీటిని వాడతారు.

ప్రశ్న 10.
ఒక కెపాసిటర్ను ఆవేశితం చేయడానికి 0.6A విద్యుత్ ప్రవాహాన్ని పంపితే ప్లేట్ల మధ్యలో స్థానభ్రంశ విద్యుత్ ప్రవాహం ఎంత?
జవాబు:
i = కెపాసిటర్లో విద్యుత్ ప్రవాహము = 0.6 A
i = i_d = ε_o\(\frac{d \phi_{\mathrm{B}}}{\mathrm{dt}}\)
∴ i = i_d = 0.6. A
∴ స్థానభ్రంశ విద్యుత్ ప్రవాహము (i_d) = 0.6 A.

స్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
ఒక విద్యుదయస్కాంత తరంగం ఏమి కలిగి ఉంటుంది? శూన్యంలో దాని వేగం ఏయే అంశాలపై ఆధారపడి ఉంటుంది?
జవాబు:
అంతరాళంలో పరస్పరం లంబంగా విద్యుత్ మరియు అయస్కాంతక్షేత్ర సదిశలు మారి విద్యుదయస్కాంత తరంగాలు జనిస్తాయని మాక్స్వెల్ భావించాడు. ఇవి అంతరాళంలో ఎలాంటి యానకం అవసరం లేకుండా ప్రయాణిస్తాయి. ఈ తరంగాలను విద్యుదయస్కాంత తరంగాలని అంటారు.

మాక్స్వెల్ భావన ప్రకారం విద్యుదయస్కాంత తరంగాలలో విద్యుత్ మరియు అయస్కాంతక్షేత్ర సదిశలు పరస్పరం లంబంగా సైన్ వక్రంగా మారుతూ, తరంగ ప్రసార దిశకు లంబంగా ఉంటాయి. అందువల్ల విద్యుదయస్కాంత తరంగాలు తిర్యక్ స్వభావాన్ని కలిగి ఉంటాయి.
విద్యుత్ క్షేత్రం E_x = E₀ Sin (Kz – ωt)
అయస్కాంత క్షేత్రం B_y0 = B₀, sin (Kz – ωt)

విద్యుదయస్కాంత తరంగాల వేగము (i) శూన్య యానకం యొక్క ప్రవేశ్యశీలత (µ_o) (ii) శూన్యయానకం యొక్క పెర్మిటివిటీ (ε_o) పై ఆధారపడును. విద్యుదయస్కాంత తరంగాల వేగము = 3 × 10⁸ m / s.

ప్రశ్న 2.
హరితగృహ ప్రభావం అంటే ఏమిటి? భూఉపరితల ఉష్ణోగ్రత పరంగా దాని పాత్ర ఏమిటి?
జవాబు:
హరిత గృహప్రభావం :
వాతావరణంలోని CO₂, CH₄, N₂, క్లోరోఫోరో కార్బన్ వంటి వాయువులు భూమి వెలువరించిన వికిరణాలను బంధించడం వల్ల భూమి యొక్క ఉష్ణోగ్రతలు పెరుగుటను హరిత గృహప్రభావం అంటారు.

1. సూర్యుడి నుండి వచ్చే వికిరణము వాతావరణంలోకి ప్రవేశించి, భూమి పై వస్తువులను వేడెక్కిస్తుంది. వాటి నుండి పరారుణ కిరణాలు ఉద్గారమవుతాయి.
2. ఈ కిరణాలు భూమి ఉపరితలం నుండి పరావర్తనం చెంది, భూవాతావరణంలో బంధించబడి, భూమి ఉష్ణోగ్రత పెరుగుతుంది.
3. కార్బన్ డయాక్సైడ్ పొరలు మరియు తక్కువ ఎత్తులో ఉండే మేఘాలు భూవాతావరణం నుండి పరారుణ కిరణాలు తప్పించుకుపోకుండా అడ్డుకుంటాయి.
4. రోజురోజుకు వాతావరణంలో కార్బన్ డయాక్సైడ్ పెరిగి, వాతావరణంలో పరారుణ కిరణాలు అధికంగా బంధించబడతాయి.
5. కాబట్టి రోజు రోజుకు భూ ఉపరితల ఉష్ణోగ్రత పెరుగుతుంది.

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 1.
విద్యుదయస్కాంత తరంగాల అవిష్కరణ సంబంధిత చరిత్రను క్లుప్తంగా తెలపండి.
జవాబు:
1. ఫారడే తన ప్రయోగాల ద్వారా విద్యుదయస్కాంత ప్రేరణను అధ్యయనం చేసినప్పుడు కాలంతో పాటు అయస్కాంతక్షేత్రం మారినప్పుడు, విద్యుత్ క్షేత్రాన్ని ఏర్పరుస్తుంది.

2. 1865 వ సంవత్సరంలో మాక్స్వెల్ తన సైద్ధాంతిక అధ్యయనం ప్రకారం, కాలంతో పాటు మారే విద్యుత్ క్షేత్రం, అయస్కాంత క్షేత్రాన్ని ఏర్పరుస్తుంది.

3. అయస్కాంత క్షేత్ర జనకం పర్యవసానంగా స్థానభ్రంశ ప్రవాహం ఏర్పడును.

4. దీనర్ధం కాలంతో పాటు మారే విద్యుత్ (లేదా) అయస్కాంతక్షేత్రాలు మరొక క్షేత్రాన్ని ఏర్పరుస్తాయి.

5. మాక్స్వెల్ భావన ప్రకారం అంతరాళంలో పరస్పరం లంబంగా మారే విద్యుత్ మరియు అయస్కాంత క్షేత్రాల సదిశల వల్ల విద్యుదయస్కాంత తరంగాలు జనిస్తాయి.

6. ఈ విద్యుదయస్కాంత తరంగాలు అంతరాళంలో ఎలాంటి యానకం అవసరం లేకుండా ప్రయాణిస్తాయి.

7. విద్యుత్ మరియు అయస్కాంతక్షేత్రాలు రెండూ అంతరాళం మరియు కాలంతో మారేటప్పుడు ఒకే పౌనఃపున్యాలను కలిగి ఉంటాయి.

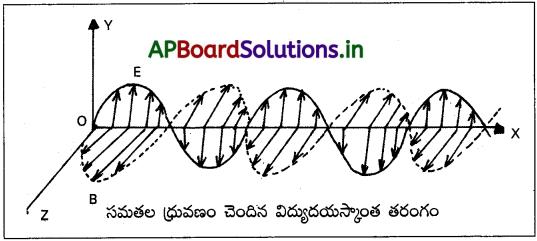
8. విద్యుత్ క్షేత్రసదిశ \(\overrightarrow{E}\) మరియు అయస్కాంతక్షేత్ర సదిశ \(\overrightarrow{B}\) లు y మరియు z అక్షం దిశలలో కంపిస్తే, x- అక్షం దిశలో విద్యుదయస్కాంత తరంగాలు ప్రసరిస్తాయి.

9. విద్యుదయస్కాంత తరంగాలు శూన్యంలో ప్రయాణించే వేగాన్ని మాక్స్వెల్ కనుగొన్నాడు.

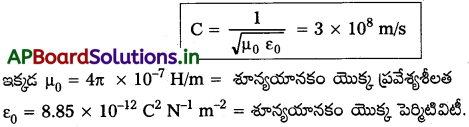
10. యానకంలో విద్యుదయస్కాంత తరంగాల వేగము v = \(\frac{1}{\sqrt{\mu \varepsilon}}\)

11. మాక్స్వెల్ భావన ప్రకారం విద్యుదయస్కాంత తరంగాలు తిర్యక్ స్వభావాన్ని కలిగి ఉంటాయి.

12. స్పార్క్ డోలకంను ఉపయోగించి 1888 లో హెర్జ్ ప్రయోగపూర్వకంగా విద్యుదయస్కాంత తరంగాలను ఉత్పత్తి చేయడం మరియు శోధించడంను వివరించాడు.

13. 1895లో జగదీష్ చంద్రబోస్ 5 m.m నుండి 25 m.m తరంగదైర్ఘ్యం గల విద్యుదయస్కాంత తరంగాలను ఉత్పత్తి చేశాడు.

14. 1899 లో మార్కొని మొట్టమొదటిగా 50 కిలోమీటర్ల దూరం వరకు పనిచేసే వైర్లెస్ సంచారవ్యవస్థను ఏర్పరిచాడు.

ప్రశ్న 2.
విద్యుదయస్కాంత తరంగాల ఆరు అభిలక్షణాలను తెలపండి. హరితగృహ ప్రభావం అంటే ఏమిటి?
జవాబు:
విద్యుదయస్కాంత తరంగాల ధర్మాలు (లేదా) అభిలక్షణాలు :
1. విద్యుదయస్కాంత తరంగాల ప్రసరణకు ఎలాంటి యానకం అవసరం లేదు. ఇవి శూన్యంలో మరియు యానకంలో ప్రసరిస్తాయి.

2. శూన్యంలో (లేదా) స్వేచ్ఛా అంతరాళంలో విద్యుదయస్కాంత తరంగాల వేగము

3. యానకంలో విద్యుదయస్కాంత తరంగాల వేగము v = \(\frac{1}{\sqrt{\mu \varepsilon}}\)

4. విద్యుదయస్కాంత తరంగాలు తిర్యక్ స్వభావాన్ని కలిగి ఉంటాయి.
విద్యుత్ క్షేత్ర సదిశ \(\overrightarrow{E}\) మరియు అయస్కాంతక్షేత్ర సదిశ \(\overrightarrow{B}\) లు పరస్పరం లంబంగా ఉండి, తరంగ ప్రసారదిశకు లంబంగా ఉంటాయి.

5. విద్యుదయస్కాంత తరంగాలు అంతరాళంలో స్వయంగా నిలకడ విద్యుత్ మరియు అయస్కాంత డోలనాలు కలిగి ఉంటాయి.

6. విద్యుదయస్కాంత తరంగాల ప్రసారశక్తి
పాయింటింగ్ సదిశ (\(\overrightarrow{P}\)) = = (\(\overrightarrow{E}\times\overrightarrow{B}\))

7. శూన్యంలో విద్యుత్ క్షేత్ర సదిశ \(\overrightarrow{E}\) మరియు అయస్కాంతక్షేత్ర సదిశల మధ్య సంబంధం. C = \(\frac{E_0}{B_0}\)

8. విద్యుదయస్కాంత తరంగాలు విద్యుత్ మరియు అయస్కాంత క్షేత్రాలలో అపవర్తనం చెందవు.

9. విద్యుదయస్కాంత తరంగాలు పరావర్తనం, వక్రీభవనం, వ్యతికరణం, వివర్తనం మరియు ధ్రువణం చెందుతాయి.

10. విద్యుదయస్కాంత తరంగాలు అధ్యారోపణ నియమాన్ని పాటిస్తాయి.

11. విద్యుదయస్కాంత తరంగాల సగటు విద్యుత్ శక్తి సాంద్రత

హరిత గృహ ప్రభావం :
వాతావరణంలోని CO₂, CH₄, N₂O, క్లోరోఫ్లోరో కార్బన్ వంటి వాయువులు భూమి వెలువరించిన వికిరణాలను బంధించడం వల్ల భూమి యొక్క ఉష్ణోగ్రతలు పెరుగుటను హరిత గృహప్రభావం అంటారు.

అభ్యాసాలు Textual Exercises

ప్రశ్న 1.
ఒక కెపాసిటర్ వృత్తాకార ప్లేట్ల వ్యాసార్థం 12cm. వీటి మధ్య దూరం 5.0 cm (పటం). ఒక బాహ్య జనకం ద్వారా (పటంలో చూపలేదు) ఈ కెపాసిటర్ను ఆవేశితం చేస్తున్నారు. ఆవేశితం చేయడానికి 0.15 Aస్థిర విద్యుత్ ప్రవాహాన్ని పంపారు.
a) కెపాసిటర్ కెపాసిటెన్స్ను లెక్కించండి ; ప్లేట్ల మధ్య పొటెన్షియల్ భేదం రేటును కనుక్కోండి.
b) ప్లేట్ల మధ్య స్థానభ్రంశ విద్యుత్ ప్రవాహం లెక్కించండి.
c) కెపాసిటర్ ప్రతి ప్లేటు వద్ద కిర్కాఫ్ మొదటి నియమం (సంధి నియమం) చెల్లుబాటు అవుతుందా? వివరించండి.

జవాబు:
పలకల వ్యాసార్ధం (r) = 12cm = 12 × 10^-2 m
రెండు వృత్తాకార పలకల మధ్య దూరం (d) = 5 cm = 5 × 10^-2 × m,
విద్యుత్ ప్రవాహం (I) = 0.15A

(b) స్థానభ్రంశ విద్యుత్, వాహన విద్యుత్కు సమానం (I_d) = 0.15 A.
(c) అవును, కిర్కాఫ్ మొదటి నియమం పాటిస్తుంది. కారణం ఇక్కడ వహన విద్యుత్ మరియు స్థానభ్రంశ విద్యుత్ల మొత్తం విద్యుత్ తీసుకుంటాం.

ప్రశ్న 2.
వ్యాసార్ధం R = 6.0 cm గల వృత్తాకార ప్లేట్లతో చేసిన సమాంతర ప్లేట్ల కెపాసిటర్ కెపాసిటెన్స్ C = 100 pF (పటం). ఈ కెపాసిటర్ను (కోణీయ) పౌనఃపున్యం 300 rad s^-1 తో గల ఒక 230 Vల a.c జనకంతో సంధానం చేశారు.

a) వహన (conduction) విద్యుత్ ప్రవాహ rms విలువ ఎంత?
b) వహన విద్యుత్ ప్రవాహ విలువ స్థానభ్రంశ విద్యుత్ ప్రవాహానికి సమానమా?
c) ప్లేట్ల మధ్యలో అక్షం నుంచి 3.0 cm వద్ద B పరిమాణం కనుక్కోండి.
జవాబు:
పలకల వ్యాసార్ధము (R) = 6 cm = 6 × 10^-2 m
కెపాసిటర్ యొక్క కెపాసిటీ (C) = 100 PF 100 × 10^-12 = 10^-10F
వోల్టేజి (V) = 230 V
పౌనఃపున్యము (ω) = 300 rad/s

b) అవును వహన ప్రవాహము, స్థానభ్రంశ ప్రవాహానికి సమానం.

c) పలకల మధ్య అక్షము నుండి బిందువు వలకు దూరం

ప్రశ్న 3.
10^-10m తరంగదైర్ఘ్యం గల X- కిరణాలకూ, 6800 Å తరంగదైర్ఘ్యం గల ఎరుపు కాంతికీ, 500 m తరంగదైర్ఘ్యం గల రేడియో తరంగాలకూ సమానమైన భౌతికరాశి ఏది?
జవాబు:
ఇక్కడ X – కిరణాలు, ఎరుపు కాంతి మరియు రేడియో తరంగాలు అన్నీ విద్యుదయస్కాంత తరంగాలు. విద్యుదయస్కాంత తరంగాలు కాంతి వేగం (C) తో ప్రయాణిస్తాయి. అందువలన X – కిరణాలు, ఎరుపు కాంతి మరియు రేడియో తరంగాలు కాంతివేగంతో ప్రయాణిస్తాయి.

ప్రశ్న 4.
ఒక సమతల విద్యుదయస్కాంత తరంగం శూన్యంలో Z – దిశలో ప్రయాణిస్తున్నది. దాని విద్యుత్, అయస్కాంత క్షేత్ర సదిశల దిశల గురించి ఏమి చెప్పగలరు? తరంగ పౌనఃపున్యం 30MHz అయితే దాని తరంగదైర్ఘ్యం ఎంత?
జవాబు:
విద్యుదయస్కాంత తరంగాల దిశ, విద్యుత్ మరియు అయస్కాంతక్షేత్రాలకు లంబంగా ఉంటుంది. విద్యుదయస్కాంత తరంగం Z – అక్షం దిశలో ప్రయాణిస్తే, విద్యుత్ మరియు అయస్కాంత క్షేత్రాలు పరస్పరం లంబంగా X-Y దిశలలో ఉంటాయి.

పౌనఃపున్యము (f) = 30MHz = 30 × 10⁶ Hz
వేగం (C) = 3 × 10⁸ m/s
C = f λ
తరంగదైర్ఘ్యము (λ) = \(\frac{3\times10^8}{30\times10^6}=\frac{300}{30}\) = 10 m

ప్రశ్న 5.
ఒక రేడియో 7.5 MHz నుంచి 12 MHz వ్యాప్తి గల బ్యాండ్లో ఏ ప్రసార కేంద్రంతో అయినా శృతి కాగలదు. ఈ బ్యాండ్కు అనురూపమైన తరంగదైర్ఘ్యం బ్యాండ్ ఏమిటి?
జవాబు:
పౌనఃపున్యము (f₁) = 7.5 MHz, (f₂) = 12 MHz,
విద్యుదయస్కాంత తరంగాల వేగం (C) = 3 × 10⁸ m/s

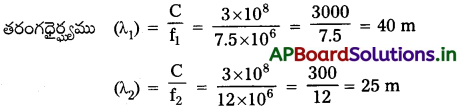
కాబట్టి తరంగదైర్ఘ్యము 25 m నుండి 40 m వరకు ఉండును.

ప్రశ్న 6.
ఒక విద్యుదావేశిత కణం తన మాధ్యమిక (సమతాస్థితి) బిందువు పరంగా 10⁹ Hz పౌనఃపున్యంతో డోలనం చేస్తున్నది. ఈ డోలకం వల్ల ఉత్పత్తి అయిన విద్యుదయస్కాంత తరంగాల పౌనఃపున్యం ఎంత?
జవాబు:
విద్యుదయస్కాంత తరంగాల పౌనఃపున్యము = 10⁹ Hz.
డోలకం ద్వారా జనించి విద్యుదయస్కాంత తరంగాల పౌనఃపున్యము, సమతాస్థితి నుండి డోలనం చెందే ఆవేశిత కణం పౌనఃపున్యానికి సమానం.

ప్రశ్న 7.
శూన్యంలో ఒక హరాత్మక విద్యుదయస్కాంత తరంగ అయస్కాంత క్షేత్ర భాగం (అంశ) దోలన పరిమితి B₀ = 510 nT. ఈ తరంగ విద్యుత్ క్షేత్ర భాగం (అంశ) దోలన పరిమితి ఎంత?
జవాబు:
అయస్కాంతక్షేత్రం B₀ = 510nT
శూన్యంలో కాంతివేగం (C) = \(\frac{E_0}{B_0}\)
E₀ అనునది తరంగం విద్యుత్ అంశభాగం
3 × 10⁸ = \(\frac{E_0}{510\times10^{-9}}\)
E₀ = 153 N/C

ప్రశ్న 8.
ఒక విద్యుదయస్కాంత తరంగ విద్యుత్ క్షేత్ర పరిమాణం E₀ = 120 N/C అనీ, దాని పౌనఃపున్యం V = 50.0 MHz. అనీ భావించండి. (a) B₀, ω, k, λ లనూ b) E, B లకు సమాసాలనూ కనుక్కోండి.
జవాబు:
విద్యుదయస్కాంత తరంగం కంపన పరిమితి E₀ = 120N/C
పౌనఃపున్యము (f) = 50 MHz 50 × 10⁶ Hz

a) శూన్యంలో కాంతివేగం

b) విద్యుత్ క్షేత్రం E = E₀ sin (kx – ωt)
E = 120 sin (1.05 × 3.14 × 10⁸ t)
అయస్కాంత క్షేత్రం B = B₀ sin (kx – wt )
B = 4 × 10^-7 sin (1.05 x -3.14 × 10⁸ t)

ప్రశ్న 9.
విద్యుదయస్కాంత తరంగ వర్ణపటంలోని వివిధ భాగాల పారిభాషిక పదాలను పాఠంలో పేర్కొన్నారు. – E = hυ సూత్రాన్ని ఉపయోగించి (వికిరణ శక్తి క్వాంటంకు: ఫోటాన్) ఫోటాన్ శక్తిని eV ప్రమాణాలలో, వివిధ విద్యుదయస్కాంత వర్ణపట భాగాలకు, కనుక్కోండి. మీరు పొందిన ఫోటాన్ శక్తుల వివిధ స్కేళ్ళు (మానాలు) ఏ (విధంగా) విద్యుదయస్కాంత వికిరణ జనకాలకు సంబంధించినవో తెలపండి.
జవాబు:
ఫోటాన్ శక్తి (E) = hν

γ – కిరణాలకు :
γ – కిరణాల పౌనఃపున్యము V = 3 × 10²⁰ Hz
γ – కిరణాల శక్తి E = hν = 6.6 × 10^-34 × 3 × 10²⁰ = 19.8 × 10^-14 J
E = \(\frac{19.8\times10^{-14}}{1.6\times10^{-19}}\) = 1.24 × 10⁶ eV
γ – కిరణాల కేంద్రక విస్ఫోటనం, సంలీనం అప్పుడు జనిస్తాయి.

X- కిరణాలకు :
పౌనఃపున్యము (v) = 3 × 10¹⁸ Hz
(E)=hv 6.6 × 10^-34 × 3 × 10²⁰ = 19.8 × 10^-14 J
E = \(\frac{19.8\times10^{-14}}{1.6\times10^{-19}}\) = 1.24 × 10⁴ eV

అత్యధిక వేగంలో ఉన్న ఎలక్ట్రాన్ త్వరణం తగ్గుట వల్ల X- కిరణాలు జనిస్తాయి.

అతినీలలోహిత కిరణాలు :
పౌనఃపున్యము (v) = 10¹⁵ Hz
(E) hv 6.6 × 10^-34 × 10¹⁵ = 6.6 × 10^-19 J
E = \(\frac{6.6\times10^{-19}}{1.6\times10^{-19}}\) = 4.125 eV

దృగ్గోచర కాంతి :

పౌనఃపున్యము (v) = 6 × 10¹⁴ Hz
శక్తి (E) = hν = 6.6 × 10^-34 × 6 × 10¹⁴ = 39.6 × 10^-20 J
E = \(\frac{39.6\times10^{-20}}{1.6\times10^{-19}}\) = 2.475 eV

పరారుణ కిరణాలు :
పౌనఃపున్యము (v) = 10¹³ Hz
శక్తి (E) = hν = 6.6 × 10^-34 × 10¹³ = 6.6 × 10^-21 J
E = \(\frac{6.6\times10^{-21}}{1.6\times10^{-19}}\) = 4.125 × 10^-2 eV

మైక్రోతరంగాలు :
పౌనఃపున్యము (v) = 10¹⁰ Hz
శక్తి (E) = hν = 6.6 × 10^-34 × 10¹⁰ 6.6 × 10^-24 J
E = \(\frac{6.6\times10^{-24}}{1.6\times10^{-19}}\) = 4.125 × 10⁵ eV

రేడియో తరంగాలు:
పౌనఃపున్యము (v) = 3 × 10⁸ Hz
శక్తి (E) = hν = 6.6 × 10^-34 × 3 × 10⁸ = 19.8 × 10^-26 J
E = \(\frac{19.8\times10^{-26}}{1.6\times10^{-19}}\) = 1.24 × 10^-6 eV

వికిరణ రకం	ఫోటాన్ శక్తి
γ – కిరణాలు	1.24 × 106 eV
X – కిరణాలు	1.24 × 104 eV
అతినీలలోహిత కిరణాలు	4.12 eV
దృగ్గోచర కాంతి	2.475 eV
పరారుణ కిరణాలు	4.125 × 10-2 eV
మైక్రో తరంగాలు	4.125 × 10-5 eV
రేడియో తరంగాలు	1.24 × 10-6 eV

ప్రశ్న 10.
ఒక సమతల విద్యుదయస్కాంత తరంగంలో విద్యుత్ క్షేత్రం జ్యావక్రీయంగా 2.0 × 10¹⁰ Hz పౌనఃపున్యంతో డోలనం చేస్తున్నది ; దోలన పరిమితి 48 Vma^-1.
a) తరంగం తరంగదైర్ఘ్యం ఎంత?
b) డోలనం చేసే అయస్కాంతక్షేత్ర దోలన పరిమితి ఎంత?
c) E క్షేత్ర సగటు శక్తి సాంద్రత, B క్షేత్ర సగటు శక్తిసాంద్రతకు సమానం అని చూపండి. [c = 3 × 10⁸ ms^-1‘].
జవాబు:
డోలన పౌనఃపున్యము = 2 × 10¹⁰ Hz
C = 3 × 10⁸m/s
విద్యుత్ క్షేత్ర కంపన పరిమితి (E₀) = 48V/m

విద్యుత్ క్షేత్ర సగటు శక్తి సాంద్రత, అయస్కాంత క్షేత్ర (B) శక్తి సాంద్రతకు సమానం.

అదనపు అభ్యాసము Additional Exercises

ప్రశ్న 11.
శూన్యంలో ఒక విద్యుదయస్కాంత తరంగ విద్యుత్ క్షేత్ర (అంశం) భాగం
E = {(3.1 N/C) cos [(1.8 rad/m) y + {5.4 × 10⁶ rad /s} t]} i.
a) తరంగ ప్రసార దిశ ఏమిటి?
b) తరంగ తరంగదైర్ఘ్యం ఎంత?
c) పౌనః పున్యం v ఎంత?
d) తరంగ అయస్కాంతక్షేత్ర భాగం డోలన పరిమితి ఎంత?
e) తరంగ అయస్కాంత క్షేత్ర భాగానికి సమాసాన్ని రాయండి.
జవాబు:
a) సమీకరణం నుండి ఇది ఋణ y – అక్షం దిశలో చలిస్తుంది. కాబట్టి – \(\hat{j}\) దిశలో చలిస్తుంది.
b) శూన్యంలో విద్యుదయస్కాంత తరంగం విద్యుత్ అంశం
E = 3.1 cos (1.84 +5.4 x 10⁶t) \(\hat{i}\)
దీనిని E = E₀ cos (ky + ωt) తో పోల్చగా
కోణీయ పౌనఃపున్యము (a) = 5.4 × 10⁶ rad/s
తరంగసంఖ్య (K) 1.8 rád/m
తరంగం యొక్క విద్యుత్ అంశం కంపన పరిమితి E₀ = 3.1N/C

e) అయస్కాంత క్షేత్ర అంశము
B = B₀ cos (ky + ωt) \(\hat{k}\)
B = 1.03 × 10⁸ cos (1.8 y + 5.4 × 10⁸ t) \(\hat{k}\)

ప్రశ్న 12.
100 W విద్యుత్ బల్బు సామర్ధ్యంలో దాదాపు 5% దృశ్య వికీరణంగా పరివర్తనం చెందింది. అయితే,
a) బల్బు నుంచి 1m దూరంలో
b) బల్బు నుండి 10m దూరంలో
దృశ్య వికిరణ సగటు తీవ్రత ఎంత? వికిరణ సమదైశికంగా ఉద్గారమౌతుందనీ, పరావర్తనాన్ని ఉపేక్షించవచ్చనీ భావించండి.
జవాబు:
మొత్తం సామర్ధ్యం = 100 W
దృగ్గోచర వికిరణ సామర్ధ్యము = మొత్తం సామర్ధ్యంలో 5% = \(\frac{5}{100}\) × 100 = 5W

a) 1m దూరంలో, శక్తి గోళాకారంగా వితరణ చెంది ఉంటే గోళం యొక్క వైశాల్యం = 4π (వ్యాసార్ధం)²

ప్రశ్న 13.
λ_m T = 0.29 cm K ఫార్ములాను ఉపయోగించి విద్యుదయస్కాంత వర్ణపటంలోని వివిధ భాగాల అభిలక్షణ ఉష్ణోగ్రతా వ్యాప్తులను కనుక్కోండి. మీరు పొందిన విలువలు (సంఖ్యలు) ఏమి చెబుతాయి?
జవాబు:
λ_m T = 0.29cm-K, λ_m = 10^-68m తీసుకుంటే

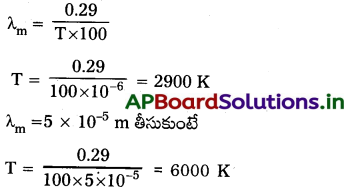
ఈ ఉష్ణోగ్రతలు విద్యుదయస్కాంత తరంగాల ఉష్ణోగ్రతల వ్యాప్తిని తెలుపుతాయి.

ప్రశ్న 14.
భౌతిక శాస్త్రంలో వివిధ సందర్భాల్లో విద్యుదయస్కాంత వికిరణాలకు సంబంధించిన ప్రముఖమైన సంఖ్యలు కింద ఇవ్వడమైంది. వీటిలో ప్రతి సంఖ్య ఏ విద్యుదయస్కాంత వర్ణపట భాగానికి సంబంధించినదో తెలపండి.
a) 21 cm (అంతర్ నక్షత్ర, అంతరాళంలోని పరమాణు హైడ్రోజన్ ఉద్గారించే తరంగదైర్ఘ్యం)
b) 1057 MHz (లాంబ్ విస్థాపనం : అత్యంత సమీపంలో ఉన్న రెండు హైడ్రోజన్ శక్తిస్థాయిల మధ్య ఎలక్ట్రాన్ సంక్రమణ వికిరణ పౌనఃపున్యం).
c) 2.7K [విశ్వారంభపు తొలి పేలుడుతో అంతరాళంలో నిండిన సమదైశిక అవశేష వికిరణ సంబంధిత ఉష్ణోగ్రత).
d) 5890 Å – 5896 Å [సోడియం జంట వర్ణపట రేఖలు]
e) 14.4 keV [అధిక పృథక్కరణ వర్ణపటశాస్త్ర పద్ధతికి సంబంధించిన ⁵⁷Fe కేంద్రకంలో ప్రత్యేక సంక్రమణంలో వెలువడిన శక్తి (మాస్బార్ (Mossbauer) వర్ణపట శాస్త్రం)].
జవాబు:
a) ఈ తరంగదైర్ఘ్యం (21 cm) రేడియో తరంగాలకు సంబంధించినది.
b) ఈ పౌనఃపున్యము (1057 MHz) కూడా రేడియో తరంగాలకు సంబంధించినది.
c) T = 2.7 K
λ_m T = 0.29 cm – K
∴ λ_m = \(\frac{0.29}{2.7}\) cm = 0.11cm
ఈ తరంగదైర్ఘ్యం మైక్రోతరంగాలకు సంబంధించినది.

d) ఈ తరంగదైర్ఘ్య అవధి దృగ్గోచర ప్రాంతానికి చెందినది.
e) శక్తి (E) = 14,4KeV = 14.4 × 10³ × 1.6 × 10^-19J

ఈ పౌనఃపున్యము X- కిరణాలకు సంబంధించినది.

ప్రశ్న 15.
కింది ప్రశ్నలకు సమాధానం తెలపండి.
a) సుదూర రేడియో ప్రసారాలకై హ్రస్వ – తరంగ బ్యాండ్ (short-wave bands) (హ్రస్వ తరంగదైర్ఘ్య వ్యాప్తి) ని వాడతారు. ఎందుకు?
b) సుదూర T.V ప్రసారాలకు ఉపగ్రహాలను వాడటం అవసరం. ఎందుకు?
c) ఖగోళ శాస్త్ర అధ్యయనానికి భూఉపరితలంపై దృశ్య, రేడియో టెలిస్కోప్ల నిర్మాణం జరిగింది. అయితే X-కిరణ ఖగోళశాస్త్ర అధ్యయనం కేవలం భూమిచుట్టూ తిరిగే కృత్రిమ ఉపగ్రహాలవల్లనే సాధ్యం. ఎందువల్ల?
d) మానవజాతి మనుగడకు స్ట్రాటో ఆవరణపైన గల సన్నటి ఓజోన్ పొర అత్యంత కీలకమైంది. ఎందుకు?
e) ఒకవేళ భూమి వాతావరణాన్ని కలిగి ఉండకపోతే, సగటు భూతల ఉష్ణోగ్రత విలువ ఇప్పటి విలువ కంటే ఎక్కువగా ఉండేదా ? తక్కువగా ఉండేదా?
f) భూగోళంపై ప్రపంచ వ్యాప్త న్యూక్లియర్ యుద్ధం తరువాత వచ్చే తీవ్రమైన న్యూక్లియర్ శీతాకాలంతో భూమిపై జీవాలకు వినాశకరమైన ఫలితం కలగబోతుందని కొంతమంది శాస్త్రజ్ఞులు భవిష్యద్దర్శనం చేశారు. ఈ భవిష్యద్దర్శనం మూలం ఏమై ఉండవచ్చు?
జవాబు:
a) రేడియో తరంగాలను ఎక్కువ దూరం ప్రసారంచేయుటకు అల్పతరంగదైర్ఘ్యాలను వాడతారు. కారణం అవి ఐనో ఆవరణం నుండి పరావర్తనం చెందుతాయి.

b) T.V ప్రసారాలకు ఉపగ్రహాలను వాడతారు కారణం T.V సంకేతాలు అధిక పౌనఃపున్యాలు కలిగి ఐనో ఆవరణము నుండి పరావర్తనం చెందవు కావున పరావర్తనం చెందించడానికి ఉపయోగిస్తారు.

c) రేడియో తరంగాలు వాతావరణం గుండా చొచ్చుకు పోతాయి కాబట్టి దృశా మరియు రేడియో టెలీస్కోప్లలో వాడతారు. కాని X- కిరణాలు తక్కువ తరంగదైర్ఘ్యం కలిగి వాతావరణంలో శోషింపబడతాయి. కావున దృశా మరియు రేడియో టెలీస్కోప్లు భూమిపై పనిచేస్తాయి. కాని X- కిరణాలను భూ వాతావరణంలో పరిభ్రమించే ఖగోళ దూరదర్శినిలలో ఉపయోగిస్తారు.

d) సన్నని ఓజోన్ పొర అతినీలలోహిత కిరణాలను అధిక భాగం శోషించుకుంటుంది. ఇవి చాలా ప్రమాదకరం, కణజాలాన్ని నష్టపరుస్తాయి. ఓజోన్ పొర అతినీలలోహిత కిరణాలు భూమిని చేరకుండా, మనలను కాపాడుతుంది.

e) భూమిపై వాతావరణం లేకపోతే, వాతావరణంలో గ్రీన్ హౌస్ ప్రభావం లేకపోతే భూవాతావరణం చల్లగా ఉంటుంది.

f) అణుయుద్ధం వలన భూమిపై మేఘాలు ఏర్పడి, సూర్యకాంతి భూమిని చేరదు. అందువలన భూమిపై శీతాకాలం వలె ఉంటుంది.

సాధించిన సమస్యలు Textual Examples

ప్రశ్న 1.
1m వ్యాసార్ధం ఉన్న వృత్తాకార ప్లేట్లుగల ఒక సమాంతర పలకల కెపాసిటర్ కెపాసిటెన్స్ 1 nF. t = 0 వద్ద ఈ కెపాసిటర్ను ఆవేశితం చేయడానికిగానూ 2 V బ్యాటరీకి,’ నిరోధం R = 1 M Ω తో శ్రేణిలో సంధానం చేశారు. t = 10^-3s తరవాత కెపాసిటర్ ప్లేట్ల అంచుకు, కేంద్రానికి సరిగ్గా మధ్యలో అయస్కాంత క్షేత్రాన్ని లెక్కించండి. కాలం t వద్ద కెపాసిటర్పై ఆవేశం q (t) = CV [1 – exp (−t/7)], ఇక్కడ కెపాసిటర్ కాల స్థిరాంకం. ఇది CR కి సమానం.
సాధన:

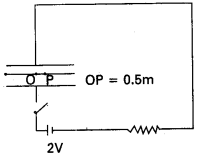
CR వలయ కాల స్థిరాంకం τ = CR = 10^-3s. అప్పుడు,
q(t) = CV [1 – exp (−t/τ)] = 2 × 10^-9 [1 – exp (−t / 10^-3]
కాలం వద్ద ప్లేట్ల మధ్య విద్యుత్ క్షేత్రం

ఇప్పుడు సమాంతర ప్లేట్లకు సమాంతరంగా వ్యాసార్థం (1/2)m ఉండేట్లు, P బిందువు ద్వారా పోయే ఒక వృత్తాకార లూప్ను ఊహించండి. ఈ లూప్ పరిధి వెంబడి అన్ని బిందువుల వద్ద అయస్కాంత క్షేత్రం B సమాన విలువను కలిగి ఉంటుంది.

ఈ లూప్ ద్వారా విద్యుత్ క్షేత్ర అభివాహం,

ప్రశ్న 2.
శూన్యంలో, X – అక్షం దిశలో ప్రయాణిస్తున్న ఒక సమతల విద్యుదయస్కాంత తరంగ పౌనఃపున్యం 25 MHz. కాల-అంతరాళంలో ఒక నిర్దిష్ట బిందువు వద్ద, E = 6.3 j V/m. ఆ బిందువు వద్ద B ఎంత?
సాధన:

దిశను కనుక్కోవడానికి, y- అక్షం వెంబడి Eని, X- అక్షం వెంబడి తరంగం ప్రసారమవుతుందని గుర్తిద్దాం. అందువల్ల x, y అక్షాలకు రెండింటికీ లంబ దిశలో B తప్పక ఉండి తీరాలి. సదిశా బీజగణితాన్ననుసరించి, Ex B x-అక్షం దిశలోనే ఉండాలి. ఎందుకంటే, (+ \(\hat{j}\)) × (+ \(\hat{k}\)) = i కాబట్టి B z- అక్షం వెంబడి ఉంటుంది.
అందువల్ల, B = 2.1 × 10^-8 \(\hat{k}\)T.

ప్రశ్న 3.
ఒక సమతల విద్యుదయస్కాంత తరంగంలోని అయస్కాంత క్షేత్రం సమీకరణం B_H = 2 × 10^-7 sin (0.5 × 10³ x + 1.5 × 10¹¹t)T.
a) తరంగం తరంగదైర్ఘ్యం, పౌనఃపున్యం ఎంత?
b) విద్యుత్ క్షేత్రానికి సమాసాన్ని వ్రాయండి.
సాధన:

b) E₀ = B₀c = 2 × 10^-7 T × 3 × 10⁸ m/s = 6 × 10¹ V/m
తరంగ ప్రసార దిశకూ, అయస్కాంత క్షేత్ర దిశకు లంబంగా విద్యుత్ క్షేత్ర అంశం ఉంటుంది. అందువల్ల, 2- అక్షం వెంబడి విద్యుత్ క్షేత్ర అంశాన్ని, E_z = 60 sin (0.5 × 10³x + 1.5 ×x 10¹¹t) V/m అని పొందవచ్చు.

ప్రశ్న 4.
ఒక అపరావర్తక తలంపై లంబంగా పతనమయ్యే కాంతి శక్తి అభివాహం 18 W/cm². తలం వైశాల్యం 20 cm² అయితే, 30 నిమిషాల కాలంపాటు తలంపై ప్రయోగించే సగటు బలం కనుక్కోండి.
సాధన:
తలంపై పతనమయ్యే మొత్తం శక్తి, U = (18 W/cm²) × (20 cm²) × (30 × 60) = 6.48 × 10⁵ J
అందువల్ల, (పూర్తి శోషణానికి) తలానికి అందిన మొత్తం ద్రవ్యవేగం,

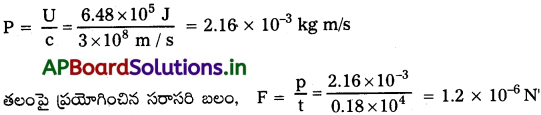
తలం పరిపూర్ణ పరావర్తకమైతే మీ సమాధానం ఎలా మారుతుంది?

ప్రశ్న 5.
దూరంలో ఉన్న 100 W విద్యుద్దీపం నుంచి వెలువడే వికిరణం వల్ల జనించే విద్యుత్, అయస్కాంతక్షేత్రాలను లెక్కించండి. దీపాన్ని బిందు జనకంగానూ, దాని దక్షతను 2.5% గానూ భావించండి.
సాధన:
బిందు జనకంగా భావించిన విద్యుద్దీపం అన్ని దిశల్లోకి ఏకరీతిగా కాంతిని వెలువరిస్తుంది. దానికి 3m దూరంలో ఉన్న ఆవరించగలిగిన గోళం ఉపరితల వైశాల్యం A = 4π² = 4π(3)² = 113 m²

పైన కనుక్కొన్న E విలువ విద్యుత్ క్షేత్రం వర్గమధ్యమ మూలం (root mean square) విలువను ఇస్తుంది. ఒక కాంతిపుంజంలోని విద్యుత్ క్షేత్రం జ్యావిక్రీయం కాబట్టి, విద్యుత్త్ర శిఖర విలువ
E_o = √2 E_rms = √2 × 2.9 V/m = 4.07 V/m

మనం చదవడానికి ఉపయోగించే కాంతి విద్యుత్ క్షేత్ర తీవ్రత చాలినంత అధికంగా ఉండటాన్ని మనం గమనిస్తాం. కొన్ని మైక్రో వోల్ట్ / మీటర్ విద్యుత్ క్షేత్ర తీవ్రత ఉండే టి.వి లేదా FM తరంగాల విద్యుత్ క్షేత్రంతో కాంతి విద్యుత్ క్షేత్ర తీవ్రతను పోల్చి చూడండి.
ఇప్పుడు మనం అయస్కాంత క్షేత్ర సత్వాన్ని (strength) లెక్కిద్దాం.

అయస్కాంత క్షేత్రపు శక్తి విద్యుత్ ప్రేరపు శక్తికి సమానమైన అయస్కాంత క్షేత్ర తీవ్రత చాలా బలహీనమైనదని స్పష్టమోతోంది.