Students can go through AP SSC 10th Class Maths Notes Chapter 6 Progressions to understand and remember the concepts easily.
AP State Syllabus SSC 10th Class Maths Notes Chapter 6 Progressions
→ The array of numbers following some rule is called a number pattern.
E.g.: 4, 6, 4, 6, 4, 6,…….
→ There is a relationship between the numbers of a pattern.
→ Each number in a pattern is called a term.
![]()
→ The series or list of numbers formed by adding or subtracting a fixed number to / from the preceding terms is called an Arithmetic Progression, simply A.P.
E.g.: 3, 5, 7,9, 11, ……
→ In the above list, each term is obtained by adding ‘2’ to the preceding term except the first term.
→ Also, we find that the difference between any two successive terms is the same throughout the series. This is called “common difference”.
→ The general form of an A.P. is
a, a + d, a + 2d, a + 3d,………, a + (n – 1) d.
Where‘a’is the first term, d is common difference.
Here d = a2 – a1 = a3 – a2 = a4 – a3 = …….. = an – an-1
→ If the number of terms of an A.P. is finite, then it is a finite A.P.
E.g.: 10, 8, 6, 4, 2.
→ If the number of terms of an A.P. is infinite, then it is an infinite A.P.
E.g.: 4, 8, 12, 16, …….
![]()
→ If d > 0, then an > an-1 and if d < 0, then an < an-1
→ The general term or nth term of an A.P is an = a + (n – 1) d.
E.g.: The 10th term of 10, 6, 2, -2, ……. is
Here a = 10 ; d = a2 – a1 = 6 – 10 = -4
∴ a10 = a + (n – 1) d = 10 + (10 – 1) × -4 = 10 – 40 + 4 = -26
→ Sum of first n-terms of an A.P. is Sn = \(\frac{n}{2}\)[a + l] where a is the first term and l is the last term.
E.g.: 1 + 2 + 3 + …… + 80 = \(\frac{80}{2}\)(1 + 80) = 40 × 81 = 3240.
→ Sum of the first n-terms of an A.P. is given by, Sn = \(\frac{n}{2}\)[2a + (n – 1)d]
Also, an = Sn – Sn-1.
→ In a series of numbers, if every number is obtained by multiplying the preceding number by a fixed number except for the first term, such arrangement is called geometric progression or G.P.
E.g.: 4, 8, 16, 32, 64,……
Here, starting from the second term, each term is obtained by multiplying the preceding term by 2.
The first term may be denoted by ‘a’, then we also see that 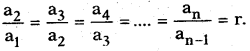
We call it “common ratio”, denoted by ‘r’
![]()
→ The general form of a G.P. is
a, ar, ar2, ar3, ……. arn-1
i.e., a1 = a, a2 = ar, a3 = ar2, an = arn-1.