AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 1 Real Numbers Ex 1.5 Textbook Questions and Answers.
AP State Syllabus SSC 10th Class Maths Solutions 1st Lesson Real Numbers Exercise 1.5
10th Class Maths 1st Lesson Real Numbers Ex 1.5 Textbook Questions and Answers
Question 1.
Determine the values of the following,
i) log255
Answer:
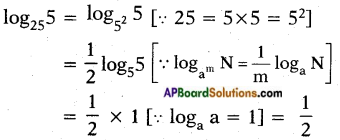
![]()
ii) log813
Answer:
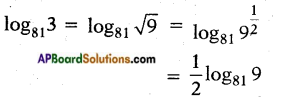
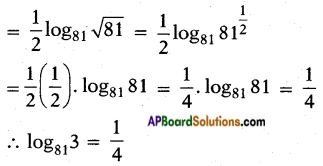
iii) log2(\(\frac{1}{16}\))
Answer:
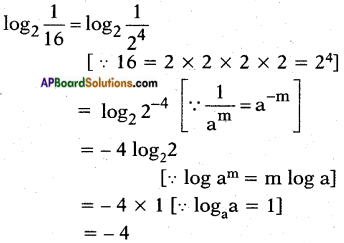
iv) log71
Answer:
log71 = log770 = 0 log77 = 0
![]()
v) logx√x
Answer:

vi) log2512
Answer:
log2512 = log229 [∵ 512 = 29]
= 9log22 [∵ log xm = m log x]
= 9 × 1 [∵ logaa = 1]
= 9
vii) log100.01
Answer:
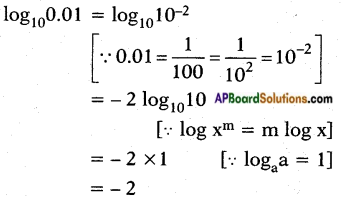
viii) \(\log _{\frac{2}{3}}\left(\frac{8}{27}\right)\)
Answer:
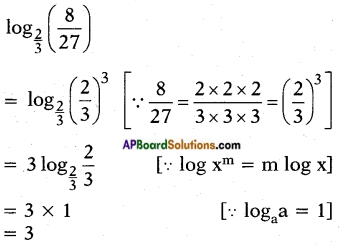
ix) \(2^{2+\log _{2} 3}\)
Answer:
\(2^{2+\log _{2} 3}\) = 22 . \(2^{\log _{2} 3}\) [∵ am . an = am+n]
= 4 × 3 [∵ \(\log _{\mathrm{a}} \mathrm{N}\) = N]
= 12
![]()
Question 2.
Write the following expressions as log N and find their values.
i) log 2 + log 5
Answer:
log 2 + log 5
= log 2 × 5 [∵ log m + log n = log mn]
= log 10
= 1
ii) log2 16 – log2 2
Answer:

iii) 3 log644
Answer:
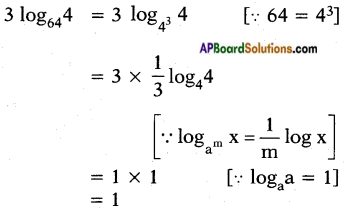
iv) 2 log 3 – 3 log 2
Answer:
2 log 3 – 3 log 2
= log 32 – log 23
= log 9 – log 8
= log \(\frac{9}{8}\)
v) log 10 + 2 log 3 – log 2
Answer:
log 10 + 2 log 3 – log 2
= log 10 + log 32 – log 2
= log 10 + log 9 – log 2 [∵ m log a = log am]
= log \(\frac{10 \times 9}{2}\) [∵ log a + log b = log ab; log a – log b = log \(\frac{a}{b}\)]
= log 45
![]()
Question 3.
Evaluate each of the following in terms of x and y, if it is given x = log23 and y = log2 5.
i) log215
Answer:
log215 = log2 3 × 5
= log23 + log25 [∵ log mn = log m + log n]
= x + y
ii) log27.5
Answer:

iii) log260
Answer:
log260 = log222 × 3 × 5
= log222 + log23 + log25
= 2 log22 + x + y
= 2 + x + y
iv) log26750
Answer:

log26750
= log22 × 33 × 53
= log22 + log233 + log253
= 1 + 3 log23 + 3 log25
= 1 + 3x + 3y
![]()
Question 4.
Expand the following,
i) log 1000
Answer:
log 1000 = log 103
= 3 log 10
= 3 × 1
= 3
ii) \(\log \left[\frac{128}{625}\right]\)
Answer:
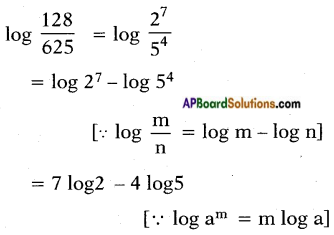
iii) log x2y3z4
Answer:
log x2y3z4 = logx2 + logy3 + logz4 [∵ log ab = log a + log b]
= 2 log x + 3 log y + 4 log z
[∵ log am = m log a]
iv) \(\log \frac{\mathbf{p}^{2} \mathbf{q}^{3}}{\mathbf{r}}\)
Answer:
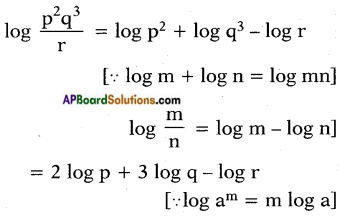
iv) \(\log \sqrt{\frac{x^{3}}{y^{2}}}\)
Answer:

![]()
Question 5.
If x2 + y2 = 25xy, then prove that 2 log (x + y) = 3log3 + logx + logy.
Answer:
Given: x2 + y2 = 25xy
We know that (x + y)2 = x2 + y2 + 2xy
= 25xy + 2xy [∵ x2 + y2 = 25xy given]
(x + y)2 = 27xy
Taking ‘log’ on both sides
log (x + y)2 = log 27xy
2 log (x + y) = log 27 + log x + log y
= log 33 + log x + log y
⇒ 2 log (x + y) = 3log3 + log x + log y
Question 6.
If \(\log \left(\frac{\mathbf{x}+\mathbf{y}}{3}\right)\) = \(\frac{1}{2}\) (log x + log y), then find the value of \(\frac{x}{y}+\frac{y}{x}\).
Answer:
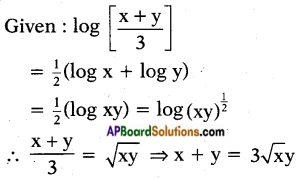
(squaring on both sides)
⇒ (x + y)2 = (3√xy)2
⇒ x2 + y2 + 2xy = 9xy
⇒ x2 + y2 = 9xy – 2xy = 7xy
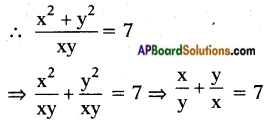
Question 7.
If (2.3)x = (0.23)y = 1000 then find the value of \(\frac{1}{x}-\frac{1}{y}\).
Answer:
Given (2.3)x = (0.23)y = 1000 = 103
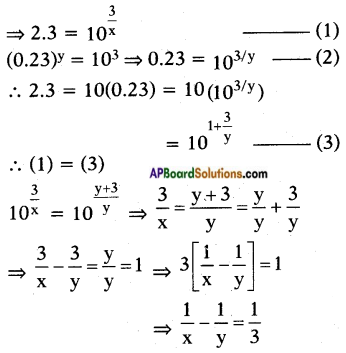
![]()
Question 8.
If 2x+1 = 31-x then find the value of x.
Answer:
Given: 2x+1 = 31-x
log 2x+1 = log 31-x
(x + 1) log 2 = (1 – x) log 3
x log 2 + log 2 = log 3 – x log 3
x log 2 + x log 3 = log 3 – log 2
x (log 3 + log 2) = log 3 – log 2
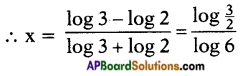
Question 9.
Is
i) log 2 is rational or irrational? Justify your answer.
Answer:
Let log102 = x
Then 10x = 2
But 2 can’t be written as 10x for any value of x
∴ log 2 is irrational.
ii) log 100 is rational or irrational? Justify your answer.
Answer:
Let log10100 = x
⇒ log10102 = x
⇒ 2 log1010 = x = 2
∴ log 100 is rational.
∴ log 100 = 2
Hence rational.