AP SSC 10th Class Maths Solutions Chapter 12 Applications of Trigonometry Optional Exercise

AP State Syllabus SSC 10th Class Maths Solutions 12th Lesson Applications of Trigonometry Optional Exercise

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 12 Applications of Trigonometry Optional Exercise Textbook Questions and Answers.

10th Class Maths 12th Lesson Applications of Trigonometry Optional Exercise Textbook Questions and Answers

Question 1.
A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After sometime, the angle of elevation reduces to 30°. Find the distance travelled by the balloon during the interval.
Answer:
Height of the balloon from the ground = 88.2 m
Height of the girl = 1.2 m
Angles of elevations = 60° and 30°

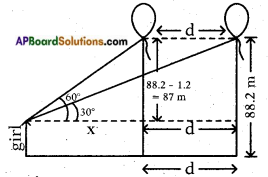
Let the distance travelled = dm
From the figure
tan 60° = \(\frac{87}{x}\)
√3 = \(\frac{87}{x}\)
⇒ 87 = √3x …….(1)
⇒ x = \(\frac{87}{\sqrt{3}}\) m
Also tan 30° = \(\frac{87}{x+d}\)
⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac{87}{x+d}\)
⇒ 87 = \(\frac{x+d}{\sqrt{3}}\) ………(2)
From equations (1) and (2)
√3x = \(\frac{x+d}{\sqrt{3}}\)
√3 × √3x = x + d
⇒ 3x = x + d
⇒ 2x = d

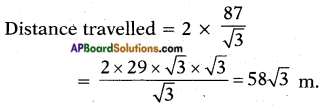
Question 2.
The angle of elevation of the top of a tower from the foot of the building is 30° and the angle of elevation of the top of the building from the foot of the tower is 60°. What is the ratio of heights of tower and building?
Answer:

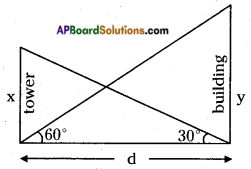
Let the height of the tower = x m
Let the height of the building = y m
Distance between the tower and building = d m.
Angle of elevation of the top of the tower = 30°.
From the figure,

∴ x : y = 1 : 3
∴ The ratio of heights of tower and building = 1 : 3.

Question 3.
The angles of elevation of the top of a lighthouse from 3 boats A, B and C in a straight line of same side of the light- house are a, 2a, 3a respectively. If the distance between the boats A and B is x meters. Find the height of lighthouse.
Answer:
From the figure,

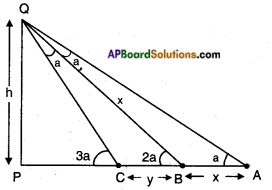
Let PQ be the height of the lighthouse = h m
A = First point of observation
B = Second point of observation
C = Third point of observation Given,
AB = x and BC = y
(Not given in the text)
Exterior angle = Sum of the opposite interior angles
∠PBQ = ∠BQA + ∠BAQ and
∠PCQ = ∠CBQ + ∠CQB
∴ AB = x = OB
By applying the sine rule,

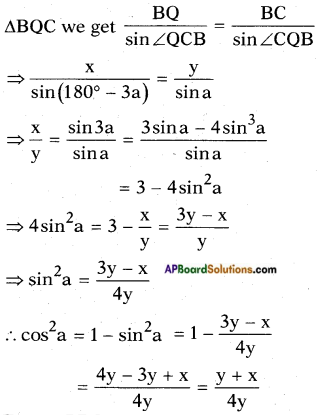
From △PBQ

Question 4.
Inner part of a cupboard is in the cuboidical shape with its length, breadth and height in the ratio 1 : √2 : 1. What is the angle made by the longest stick which can be inserted cupboard with its base inside?
Answer:

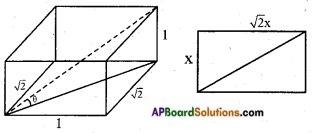
The ratio of the length, breadth and height = 1 : √2 : 1
Let its length be = x
breadth = √2x height = x
The longest stick that can be placed on the base is along its hypotenuse

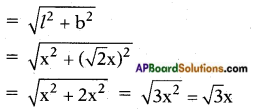
[!! Again, the longest stick that can be inserted in the cup board is along the line join of the bottom corn on with’ its opposite top corner, i.e., along the hypotenuse of the right triangle formed by height of the cup board, hypotenuse of the base and the line join of bottom corner with its opposite top corner.

Length of the largest stick = \(\sqrt{(\sqrt{3} x)^{2}+x^{2}}\)
= \(\sqrt{3 x^{2}+x^{2}}\)
= \(\sqrt{4 x^{2}}\) = 2x]
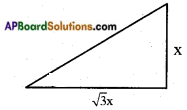
Now the angle made by the largest stick be = θ

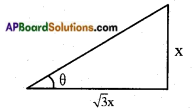
Then tan θ = \(\frac{\text { opp. side }}{\text { adj. side }}\) = \(\frac{x}{\sqrt{3} x}\) = \(\frac{1}{\sqrt{3}}\)
tan θ = tan 30°
∴ θ = 30°.

Question 5.
An iron spherical ball of volume 232848 cm³ has been melted and converted into a cone with the vertical angle of 120°. What are its height and base?
Answer:
Volume of the spherical ball = Volume of the cone

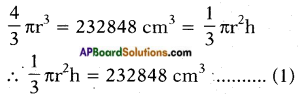
Given that vertical angle = 60°

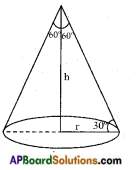
Let its height be h cm. and radius r cm.
From the figure
Also tan 30° = \(\frac{h}{r}\)
⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac{h}{r}\)
∴ h = \(\frac{r}{\sqrt{3}}\)
Substituting h = \(\frac{r}{\sqrt{3}}\) equation (1) we get

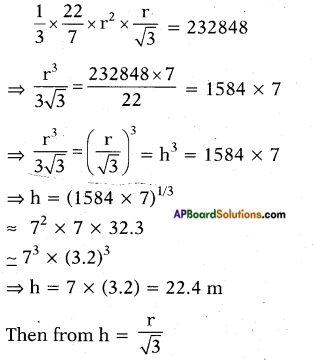
⇒ r = h√3 = (22.4) (1.732) = 38.79 m
r = 38.79 cm and h = 22.4 cm.