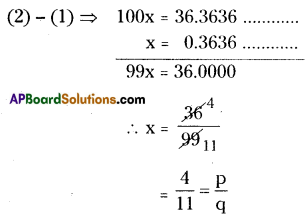AP State Syllabus AP Board 8th Class Maths Solutions Chapter 1 Rational Numbers Ex 1.3 Textbook Questions and Answers.
AP State Syllabus 8th Class Maths Solutions 1st Lesson Rational Numbers Exercise 1.3
![]()
Question 1.
Express each of the following decimal in the \(\frac{p}{q}\) form.
(i) 0.57 (ii) 0.176 (iii) 1.00001 (iv) 25.125
Solution:
(i) 0.57 = \(\frac{57}{100}\) (∵ two digits are there after the decimal poing)
(ii) 0.176 = \(\frac{176}{1000}\)
(iii) 1.00001 = \(\frac{100001}{100000}\)
(iv) 25.125 = \(\frac{25125}{1000}\)
Question 2.
Express each of the following decimals in the rational form \(\frac{p}{q}\)
(1) \(0 . \overline{9}\)
(ii) \(0 . \overline{57}\)
(iii) \(0 .7 \overline{29}\)
(iv) \(12.2 \overline{8}\)
Solution:
(i) \(0 . \overline{9}\)
Let x = \(0 . \overline{9}\)
⇒ x = 0.999 ………………. (1)
Here periodicity is 1. So, equation (1) should be multiplied both sides with
= 10 × x = 10 × 0.999
10 x = 9.999 ………….. (2)
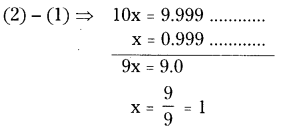
\(0 . \overline{9}\) = 1
![]()
Second Method:
\(0 . \overline{9}=0+\overline{9}=0+\frac{9}{9}\)
= 0 + 1 = 1
(ii) \(0 . \overline{57}\)
x = \(0 . \overline{57}\) ⇒ x = 0.5757…………(1)
Here periodicity is 2. So, we should multiply with 100
⇒ 100 × x = 100 x 0.5757 …………..
100 × =57.57 ……………………. (2)

(iii) \(0 .7 \overline{29}\)
x = \(0 .7 \overline{29}\)
x = \(0 .7 \overline{29}\) ⇒ x = 0.7979…………(1)
Here periodicity is 2. So, equation (1) should multiply with 100
⇒ 100 × x = 100 × 0.72929 …………..
100 × = 72.929 …………………… (2)

![]()
(iv) \(12.2 \overline{8}\)
x = (iv) \(12.2 \overline{8}\)
⇒ x = 12.288 ………..(1)
Here periodicity is 1. So, equation (1) should multiply with 10
⇒ 100 × x = 100 × 12.288 …………..
10 x = 122.888 …………………… (2)

Question 3.
Find(x + y) ÷ (x – y) if
(i) x = \(\frac{5}{2}\), y = \(-\frac{3}{4}\)
(ii) x = \(\frac{1}{4}\), y = \(\frac{3}{2}\)
Solution:
If x = \(\frac{5}{2}\), y = \(-\frac{3}{4}\) then

ii) x = \(\frac{1}{4}\), y = \(\frac{3}{2}\)

![]()
Question 4.
Divide the sum of \(-\frac{13}{5}\) and \(\frac{12}{7}\) by the product of \(-\frac{13}{7}\) and \(-\frac{1}{2}\)
Solution:
Sum of \(-\frac{13}{5}\) and \(\frac{12}{7}\)
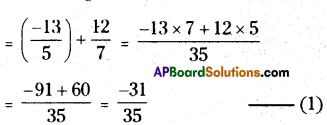
the product of \(-\frac{13}{7}\) and \(-\frac{1}{2}\)

Question 5.
If \(\frac{2}{5}\) of a number exceeds \(\frac{1}{7}\) of the same number by 36. Find the number.
Solution:
Let the number be ‘x’ say.
\(\frac{2}{5}\) part of x = \(\frac{2}{5}\) × x = \(\frac{2x}{5}\)
\(\frac{1}{7}\) part of x = \(\frac{1}{7}\) × x = \(\frac{x}{7}\)
∴ According to the sum,

Question 6.
Two pieces of lengths 2\(\frac{2}{5}\) m and 3\(\frac{3}{10}\) mare cut off from a rope 11 m long. What is the length of the remaining rope?
Soltuion:
The length of the remaining rope

∴ The length of remaining rope
= 5\(\frac{1}{10}\) mts.
![]()
Question 7.
The cost of 7\(\frac{2}{3}\) meters of cloth is ₹12\(\frac{3}{4}\) . Find the cost per metre.
Solution:
The cost of 7\(\frac{2}{3}\) mts (\(\frac{23}{3}\) mts ) of cloth
= ₹ \(12 \frac{3}{4}\) = ₹ \(\frac{51}{4}\)
∴ The cost of 1m cloth
= \(\frac{51}{4} \div \frac{23}{3}=\frac{51}{4} \times \frac{3}{23}=\frac{153}{92}\) = ₹ 1.66
Question 8.
Find the area of a rectangular park which is 18\(\frac{3}{5}\)m long and 8\(\frac{2}{3}\) in broad.
Solution:
The length of the rectangular park
= 18\(\frac{3}{5}\)m = \(\frac{93}{5}\)
Its width / breath = 8\(\frac{2}{3}\) m = \(\frac{26}{3}\) m
∴ Area of the rectangular park
(A) = l × b

Question 9.
What number should \(-\frac{33}{16}\) be divided by to get \(-\frac{11}{4}\)
Solution:
Let the dividing number be ‘x’ say.

![]()
Question 10.
If 36 trousers of equal sizes can be stitched with 64 meters of cloth. What is the length of the cloth required for each trouser?
Solution:
36 trousers of equal sizes can he stitched with 64 mts of cloth, then the length of the cloth ¡s required for each trouser
= 64 ÷ 36
= \(\frac{64}{36}=\frac{16}{9}\) = 1 \(\frac{7}{9}\)
![]()
Question 11.
When the repeating decimal 0.363636 …. is written in simplest fractional form\(\frac{p}{q}\) , find the sum p+ q.
Solution:
x = 0.363636………………………….. (1)
Here periodicity is ‘2’. So, equation (1) should be multiplied both sides with 100.
⇒ 100 × x = 100 × 0.363636 …………..
100 x = 36.3636 ………..(2)