AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 6 Progressions Ex 6.2 Textbook Questions and Answers.
AP State Syllabus SSC 10th Class Maths Solutions 6th Lesson Progressions Exercise 6.2
10th Class Maths 6th Lesson Progressions Ex 6.2 Textbook Questions and Answers
Question 1.
Fill in the blanks in the following table, given that ‘a’ is the first term, d the common difference and an the nth term of the A.P:
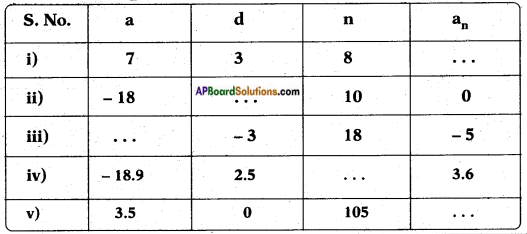
Answer:

![]()
Question 2.
Find the i) 30th term of the A.P.: 10, 7, 4,……
ii) 11th term of the A.P.: -3, –\(\frac{1}{2}\), 2,…
Answer:
i) Given A.P. = 10, 7, 4, …….
a1 = 10; d = a2 – a1 = 7 – 10 = – 3
an = a + (n – 1) d
a30 = 10 + (30 – 1) (- 3) = 10 + 29 × (- 3) = 10 – 87 = – 77
ii) Given A.P. = – 3, –\(\frac{1}{2}\), 2,…
a1 = -3; d = a2 – a1 = –\(\frac{1}{2}\) – (-3) = – 3
= –\(\frac{1}{2}\) + 3
= \(\frac{-1+6}{2}\)
= \(\frac{5}{2}\)
an = a + (n – 1) d
= -3 + (11-1) × \(\frac{5}{2}\)
= -3 + 10 × \(\frac{5}{2}\)
= -3 + 5 × 5
= -3 + 25
= 22
Question 3.
Find the respective terms for the following APs.
i) a1 = 2; a3 = 26, find a2.
Answer:
Given: a1 = a = 2 …….. (1)
a3 = a + 2d = 26 …….. (2
Equation (2) – equation (1)
⇒ (a + 2d) – a = 26 – 2
⇒ 2d = 24
d = \(\frac{24}{2}\) = 12
Now a2 = a + d = 2 + 12 = 14
ii) a2 = 13; a4 = 3, find a1, a3.
Answer:
Given: a2 = a + d = 13 ….. (1)
a4 = a + 3d = 3 ….. (2)
Solving equations (1) and (2);
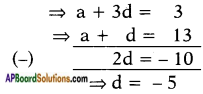
∴ Substituting d = – 5 in equation (1) we get
a + (-5) = 13
∴ a = 13 + 5 = 18 i.e., a1 = 18
a3 = a + 2d = 18 + 2(- 5)
= 18 – 10 = 8
iii) a1 = 5; a4 = 9\(\frac{1}{2}\), find a2, a3.
Answer:
Given: a1 = a = 5 ….. (1)
a4 = a + 3d = 9\(\frac{1}{2}\) ….. (2)
Solving equations (1) and (2);

⇒ 3d = 4\(\frac{1}{2}\)
⇒ 3d = \(\frac{9}{2}\)
⇒ d = \(\frac{9}{2 \times 3}\) = \(\frac{3}{2}\)
∴ a2 = a + d = 5 + \(\frac{3}{2}\) = \(\frac{13}{2}\)
a3 = a + 2d = 5 + 2 × \(\frac{3}{2}\) = 5 + 3 = 8
![]()
iv) a1 = -4; a6 = 6, find a2, a3, a4, a5.
Answer:
Given: a1 = a = -4 ….. (1)
a6 = a + 5d = 6 ….. (2)
Solving equations (1) and (2);
(-4) + 5d = 6
⇒ 5d = 6 + 4
⇒ 5d = 10
⇒ d = \(\frac{10}{5}\)
Now
∴ a2 = a + d = -4 + 2 = -2
a3 = a + 2d = -4 + 2 × 2 = -4 + 4 = 0
a4 = a + 3d = -4 + 3 × 2 = -4 + 6 = 2
a5 = a + 4d = -4 + 4 × 2 = -4 + 8 = 4
v) a2 = 38; a6 = -22, find a1, a3, a4, a5.
Answer:
Given: a2 = a + d = 38 ….. (1)
a6 = a + 5d = -22 ….. (2)
Subtracting (2) from (1) we get
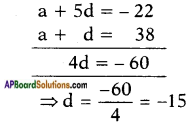
Now substituting, d = – 15 in equation (1), we get
a + (- 15) = 38 ⇒ a = 38 + 15 = 53
Thus,
a1 = a = 53;
a3 = a + 2d = 53 + 2 × (- 15) = 53 – 30 = 23;
a4 = a + 3d = 53 + 3 × (- 15) = 53 – 45 = 8;
a5 = a + 4d = 53 + 4 × (- 15) = 53 – 60 = – 7
Question 4.
Which term of the AP:
3, 8, 13, 18,…, is 78?
Answer:
Given: 3, 8, 13, 18, ……
Here a = 3; d = a2 – a1 = 8 – 3 = 5
Let ‘78’ be the nth term of the given A.P.
∴ an = a + (n – 1) d
⇒ 78 = 3 + (n – 1) 5
⇒ 78 = 3 + 5n – 5
⇒ 5n = 78 + 2
⇒ n = \(\frac{80}{2}\) = 16
∴ 78 is the 16th term of the given A.P.
Question 5.
Find the number of terms in each of the following APs:
i) 7, 13, 19, ….., 205
Answer:
Given: A.P: 7, 13, 19, ……….
Here a1 = a = 7; d = a2 – a1 = 13 – 7 = 6
Let 205 be the nth term of the given A.P.
Then, an = a + (n – 1) d
205 = 7 + (n- 1)6
⇒ 205 = 7 + 6n – 6
⇒ 205 = 6n + 1
⇒ 6n = 205 – 1 = 204
∴ n = \(\frac{204}{6}\) = 34
∴ 34 terms are there.
![]()
ii) 18, 15\(\frac{1}{2}\), 13, …, -47
Answer:
Given: A.P: 18, 15\(\frac{1}{2}\), 13, …….
Here a1 = a = 18;
d = a2 – a1 = 15\(\frac{1}{2}\) – 18 = -2\(\frac{1}{2}\) = –\(\frac{5}{2}\)
Let ‘-47’ be the nth term of the given A.P.
an = a + (n – 1) d
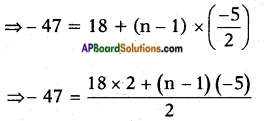
⇒ -94 = 36 – 5n + 5
⇒ 5n = 94 + 41
⇒ n = \(\frac{135}{5}\) = 27
∴ 27 terms are there.
Question 6.
Check whether, -150 is a term of the AP: 11, 8, 5, 2…
Answer:
Given: A.P. = 11, 8, 5, 2…
Here a1 = a = 11;
d = a2 – a1 = 8 – 11 = -3
If possible, take – 150 as the nth term of the given A.P.
an = a + (n – 1) d
⇒ -150 = 11 + (n – 1) × (-3)
⇒ -150 = 11 – 3n + 3
⇒ 14 – 3n = – 150
⇒ 3n= 14 + 150 = 164
∴ n = \(\frac{164}{3}\) = 54\(\frac{2}{3}\)
Here n is not an integer.
∴ -150 is not a term of the given A.P.
Question 7.
Find the 31st term of an A.P. whose 11th term is 38 and the 16th term is 73.
Answer:
Given: An A.P. whose
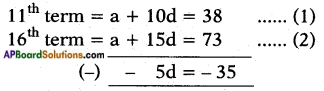
⇒ -5d = -35
⇒ d = \(\frac{-35}{-5}\) = 7
Substituting d = 7 in the equation (1)
we get,
a + 10 x 7 = 38
⇒ a + 70 = 38
⇒ a = 38 – 70 = -32
Now, the 31st term = a + 30d
= (-32) + 30 × 7
= -32 + 210 = 178
![]()
Question 8.
If the 3rd and the 9th terms of an A.P are 4 and -8 respectively, which term of this A.P is zero?
Answer:
Given: An A.P. whose
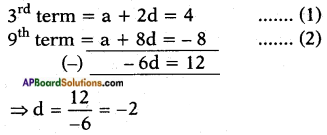
Substituting d = -2 in equation (1) we get
a + 2 × (-2) = 4
⇒ a – 4 = 4
⇒ a = 4 + 4 = 8
Let nth term of the given A.P be equal to zero.
an = a + (n – 1)d
⇒ 0 = 8 + (n – 1) × (-2)
⇒ 0 = 8 – 2n + 2
⇒ 10 – 2n = 0
⇒ 2n = 10 and n = \(\frac{10}{2}\) = 5
∴ The 5th term of the given A.P is zero.
Question 9.
The 17th term of an A.P exceeds its 10 term by 7. Find the common difference.
Answer:
Given an A.P in which a17 = a10 + 7
⇒ a17 – a10 = 7
We know that an = a + (n – 1)d

⇒ d = \(\frac{7}{7}\) = 1
Question 10.
Two APs have the same common difference. The difference between their 100th terms is 100, what is the difference between their 1000th terms?
Answer:
Let the first A.P be:
a, a + d, a + 2d, ……..
Second A.P be:
b, b + d, b + 2d, b + 3d, ………
Also, general term, an = a + (n – 1)d
Given that, a100 – b100 = 100
⇒ a + 99d – (b + 99d) = 100
⇒ a – b = 100
Now the difference between their 1000th terms,

∴ The difference between their 1000th terms is (a – b) = 100.
Note: If the common difference for any two A.Ps are equal then difference between nth terms of two A.Ps is same for all natural values of n.
![]()
Question 11.
How many three-digit numbers are divisible by 7?
Answer:
The least three digit number is 100.

∴ The least 3 digit number divisible by 7 is 100 + (7 – 2) = 105
The greatest 3 digit number is 999

∴ The greatest 3 digit number divisible by 7 is 999 – 5 = 994.
∴ 3 digit numbers divisible by 7 are
105, 112, 119,….., 994.
a1 = a = 105; d = 7; an = 994
an = a + (n – 1)d
⇒ 994 = 105 + (n – 1)7
⇒ (n – 1)7 = 994 – 105
⇒ (n – 1)7 = 889
⇒ n – 1 = \(\frac{889}{7}\) = 127
∴ n = 127 + 1 = 128
∴ There are 128, 3 digit numbers which are divisible by 7.
(or)
\(\frac{\text { last number – first number }}{7}\)
\(\frac{999-100}{7}\)
≃ 128.4 = 128 numbers divisible by 7.
Question 12.
How many multiples of 4 lie between 10 and 250?
Answer:
Given numbers: 10 to 250

∴ Multiples of 4 between 10 and 250 are
First term: 10 + (4 – 2) = 12
Last term: 250 – 2 = 248
∴ 12, 16, 20, 24, ….., 248
a = a1 = 12; d = 4; an = 248
an = a + (n – 1)d
248 = 12 + (n – 1) × 4
⇒ (n – 1)4 = 248 – 12
⇒ n – 1 = \(\frac{236}{4}\) = 59
∴ n = 59 + 1 = 60
There are 60 numbers between 10 and 250 which are divisible by 4.
![]()
Question 13.
For what value of n, are the nth terms of two APs: 63, 65, 67, ….. and 3, 10, 17,… equal?
Answer:
Given : The first A.P. is 63, 65, 67, ……
where a = 63, d = a2 – a1,
⇒ d = 65 – 63 = 2
and the second A.P. is 3, 10, 17, …….
where a = 3; d = a2 – a1 = 10 – 3 = 7
Suppose the nth terms of the two A.Ps are equal, where an = a + (n – 1)d
⇒ 63 + (n – 1)2 = 3 + (n – 1)7
⇒ 63 + 2n – 2 = 3 + 7n – 7
⇒ 61 + 2n = 7n – 4
⇒ 7n – 2n = 61 + 4
⇒ 5n = 65
⇒ n = \(\frac{65}{5}\) = 13
∴ 13th terms of the two A.Ps are equal.
Question 14.
Determine the AP whose third term is 16 and the 7th term exceeds the 5th term by 12.
Answer:
Given : An A.P in which
a3 = a + 2d = 16 …… (1)
and a7 = a5 + 12
i.e., a + 6d = a + 4d + 12
⇒ 6d – 4d = 12
⇒ 2d = 12
⇒ d = \(\frac{12}{2}\) = 6
Substituting d = 6 in equation (1) we get
a + 2 × 6 = 16
⇒ a = 16 – 12 = 4
∴ The series/A.P is
a, a + d, a + 2d, a + 3d, …….
⇒ 4, 4 + 6, 4 + 12, 4 + 18, ……
⇒ A.P.: 4, 10, 16, 22, …….
Question 15.
Find the 20th term from the end of the AP: 3, 8, 13,…, 253.
Answer:
Given: An A.P: 3, 8, 13, …… , 253
Here a = a1 = 3
d = a2 – a1 = 8 – 3 = 5
an = 253, where 253 is the last term
an = a + (n – l)d
∴ 253 = 3 + (n – 1)5
⇒ 253 = 3 + 5n – 5
⇒ 5n = 253 + 2
⇒ n = \(\frac{255}{5}\) = 51
∴ The 20th term from the other end would be
1 + (51 – 20) = 31 + 1 = 32
∴ a32 = 3 + (32 – 1) × 5
= 3 + 31 × 5
= 3 + 155 = 158
![]()
Question 16.
The sum of the 4th and 8th terms of an AP is 24 and the sum of the 6th and 10th terms is 44. Find the first three terms of the AP.
Answer:
Given an A.P in which a4 + a8 = 24
⇒ a + 3d + a + 7d = 24
⇒ 2a + 10d = 24
⇒ a + 5d = 12 ……. (1)
and a6 + a10 = 44
⇒ a + 5d + a + 9d = 44
⇒ 2a + 14d = 44
⇒ a + 7d = 22 ……. (2)
Also a + 5d = 12
⇒ a + 5(5) = 12
⇒ a + 25 = 12
⇒ a = 12 – 25 = -13
∴ The A.P is a, a + d, a + 2d, ……
i.e., – 13, (- 13 + 5), (-13 + 2 × 5)…
⇒ -13, -8, -3, …….
Question 17.
Subba Rao started work in 1995 at an annual salary of Rs. 5000 and received an increment of Rs. 200 each year. In which year did his income reach Rs. 7000?
Answer:
Given: Salary of Subba Rao in 1995 = Rs. 5000
Annual increment = Rs. 200
i.e., His salary increases by Rs. 200 every year.

Clearly 5000, 5200, 5400, forms an A.P in which a = 5000 and d = 200.
Now suppose that his salary reached Rs. 7000 after x – years.
i.e., an = 7000
But, an = a + (n – 1)d
7000 = 5000 + (n – 1)200
⇒ 7000 – 5000 = (n – 1)200
⇒ n – 1 = \(\frac{2000}{200}\) = 10
⇒ n = 10 + 1
∴ In 11th year his salary reached Rs. 7000.