AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 7 Coordinate Geometry Ex 7.1 Textbook Questions and Answers.
AP State Syllabus SSC 10th Class Maths Solutions 7th Lesson Coordinate Geometry Exercise 7.1
10th Class Maths 7th Lesson Coordinate Geometry Ex 7.1 Textbook Questions and Answers
Question 1.
Find the distance between the following pair of points,
(i) (2, 3) and (4, 1)
Answer:
Distance = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{(4-2)^{2}+(1-3)^{2}}\)
= \(\sqrt{4+4}\)
= √8 = 2√2 units
ii) (- 5, 7) and (-1, 3)
Answer:
Distance = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{(-1+5)^{2}+(3-7)^{2}}\)
= \(\sqrt{4^{2}+(-4)^{2}}\)
= \(\sqrt{16+16}\)
= √32 = 4√2 units
iii) (- 2, -3) and (3, 2)
Answer:

iv) (a, b) and (- a, – b)
Answer:
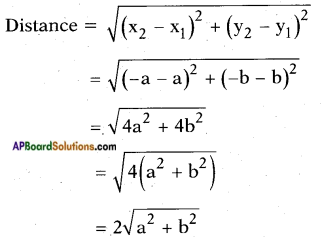
![]()
Question 2.
Find the distance between the points (0, 0) and (36, 15).
Answer:
Given: Origin O (0, 0) and a point P (36, 15).
Distance between any point and origin = \(\sqrt{x^{2}+y^{2}}\)
∴ Distance = \(\sqrt{36^{2}+15^{2}}\)
= \(\sqrt{1296+225}\)
= \(\sqrt{1521}\)
= 39 units

∴ 1521 = 32 × 132
\(\sqrt{1521}\) = 3 × 13 = 39
Question 3.
Verify that the points (1, 5), (2, 3) and (-2, -1) are collinear or not.
Answer:
Given: A (1, 5), B (2, 3) and C (- 2, – 1)

Here the sum of no two segments is equal to third segment.
Hence the points are not collinear.
!! Slope of AB, m1 = \(\frac{3-5}{2-1}\) = -2
Slope of BC, m2 = \(\frac{-1-3}{-2-2}\) = 1
m1 ≠ m2
Hence A, B, C are not collinear.
![]()
Question 4.
Check whether (5, -2), (6, 4) and (7,-2) are the vertices of an isosceles triangle.
Answer:
Let A = (5, – 2); B = (6, 4) and C = (7, – 2).
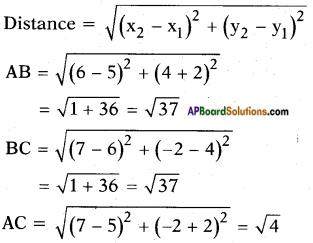
Now we have, AB = BC.
∴ △ABC is an isosceles triangle,
i.e., given points are the vertices of an isosceles triangle.
Question 5.
In a classroom, 4 friends are seated at the points A, B, C and D as shown in figure. Jarina and Phani walk into the class and after observing for a few minutes Jarina asks Phani “Don’t you think ABCD is a square?” Phani disagrees. Using distance formula, find which of them is correct. Why?
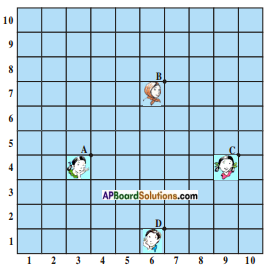
Answer:
Given: Four friends are seated at A, B, C and D where A (3, 4), B (6, 7), C (9, 4) and D (6, 1).
Now distance

BD = \(\sqrt{(6-6)^{2}+(1-7)^{2}}\) = √36 = 6
Hence in □ ABCD four sides are equal
i.e., AB = BC = CD = DA
= 3√2 units
and two diagonals are equal.
i.e., AC = BD = 6 units.
∴ □ ABCD forms a square.
i.e., Jarina is correct.
![]()
Question 6.
Show that the following points form an equilateral triangle A(a, 0), B(- a, 0), C(0, a√3).
Answer:
Given: A (a, 0), B (- a, 0), C (0, a√3).

Now, AB = BC = CA.
∴ △ABC is an equilateral triangle.
Question 7.
Prove that the points (-7, -3), (5, 10), (15, 8) and (3, -5) taken in order are the corners of a parallelogram.
Answer:
To show that the given points form a parallelogram.
We have to show that the mid points of each diagonal are same. Since diagonals of a parallelogram bisect each other.
Now let A(-7, -3), B(5, 10), C(15, 8) and D(3, -5)
Then midpoint of diagonal
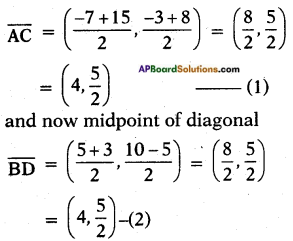
∴ (1) = (2)
Hence the given are vertices of a parallelogram.
![]()
Question 8.
Show that the points (-4, -7), (-1, 2), (8, 5) and (5, -4) taken in order are the vertices of a rhombus. And find its area.
(Hint: Area of rhombus = \(\frac{1}{2}\) × product of its diagonals)
Answer:
Given in ▱ ABCD , A(-4, – 7), B (- 1, 2), C (8, 5) and D (5,-4)
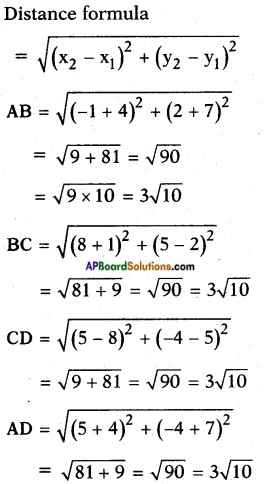

∴ In ▱ ABCD, AB = BC = CD = AD [from sides are equal]
Hence ▱ ABCD is a rhombus.
Area of a rhombus = \(\frac{1}{2}\) d1d2
= \(\frac{1}{2}\) × 12√2 × 6√2
= 72 sq. units.
Question 9.
Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer.
i) (-1,-2), (1,0), (-1,2), (-3,0)
Answer:
Let A (- 1, -2), B (1, 0), C (- 1, 2), D (- 3, 0) be the given points. Distance formula

In ▱ ABCD, AB = BC = CD = AD – four sides are equal.
AC = BD – diagonals are equal.
Hence, the given points form a square,
![]()
ii) (-3, 5), (1, 10), (3, 1), (-1,-4).
Answer:
Let A(-3, 5), B(l,10), C(3, 1), D(-l, -4) then

In ▱ ABCD, \(\overline{\mathrm{AB}}\) = \(\overline{\mathrm{CD}}\) and \(\overline{\mathrm{BC}}\) = \(\overline{\mathrm{AD}}\) (i.e., both pairs of opposite sides are equal) and \(\overline{\mathrm{AC}}\) ≠ \(\overline{\mathrm{BD}}\).
Hence ▱ ABCD is a parallelogram,
i.e., The given points form a parallelogram.
iii) (4, 5), (7, 6), (4, 3), (1, 2).
Answer:
Let A (4, 5), B (7, 6), C (4, 3) and D (1, 2) be the given points.
Distance formula
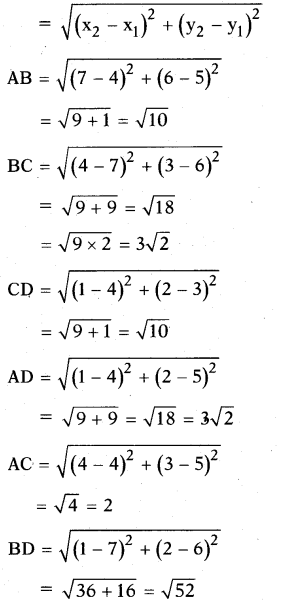
In ▱ ABCD, AB = CD and BC = AD (i.e., both pairs of opposite sides are equal) and AC ≠ BD.
Hence ▱ ABCD is a parallelogram, i.e., The given points form a parallelogram.
![]()
Question 10.
Find the point on the X-axis which is equidistant from (2, -5) and (-2,9).
Answer:
Given points, A (2, – 5), B (- 2, 9).
Let P (x, 0) be the point on X – axis which is equidistant from A and B. i.e., PA = PB.
Distance formula = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)

But PA = PB.
⇒ \(\sqrt{x^{2}-4 x+29}=\sqrt{x^{2}+4 x+85}\)
Squaring on both sides, we get
x2 – 4x + 29 = x2 + 4x + 85
⇒ – 4x – 4x = 85 – 29
⇒ – 8x = 56
⇒ x = \(\frac{56}{-8}\) = -7
∴ (x, 0) = (- 7, 0) is the point which is equidistant from the given points.
Question 11.
If the distance between two points (x, 7) and (1, 15) is 10, find the value of x.
Answer:
Formula for distance between two points = \(\sqrt{\left(x_{1}-x_{2}\right)^{2}+\left(y_{1}-y_{2}\right)^{2}}\)
Now distance between (x, 7) and (1,15) is 10.
∴ \(\sqrt{(x-1)^{2}+(7-15)^{2}}\) = 10
∴ (x – l)2 + (-8)2 = 102
⇒ (x – l)2 = 100 – 64 = 36
∴ x – 1 = √36 = ± 6
∴ x – 1 = 6 or x – 1 = -6
⇒ x = 6 + 1 = 7 or x = -6 + 1 = -5
∴ x = 7 or x = – 5
![]()
Question 12.
Find the values of y for which the distance between the points P(2, -3) and Q(10, y) is 10 units.
Answer:
Given: P (2, – 3), Q (10, y) and
\(\overline{\mathrm{PQ}}\) = 10.
Distance formula = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)

⇒ y2 + 6y + 73 = 100
⇒ y2 + 6y – 27 = 0
⇒ y2 + 9y – 3y – 27 = 0
⇒ y (y + 9) – 3 (y + 9) = 0
⇒ (y + 9) (y – 3) = 0
⇒ y + 9 = 0 or y – 3 = 0
⇒ y = -9 or y = 3
⇒ y = – 9 or 3.
Question 13.
Find the radius of the circle whose centre is (3, 2) and passes through (-5,6).
Answer:
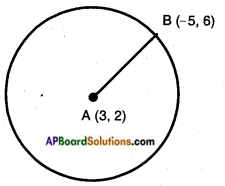
Given: A circle with centre A (3, 2) passing through B (- 5, 6).
Radius = AB
[∵ Distance of a point from the centre of the circle]
Distance formula = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
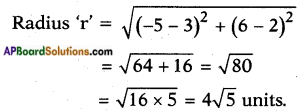
![]()
Question 14.
Can you draw a triangle with vertices (1, 5), (5, 8) and (13, 14)? Give reason.
Answer:
Let A (1, 5), B (5, 8) and C (13, 14) be the given points.
Distance formula
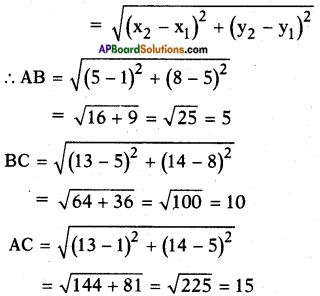
Here, AC = AB + BC.
∴ △ABC can’t be formed with the given vertices.
[∵ Sum of the any two sides of a triangle must be greater than the third side].
Question 15.
Find a relation between x and y such that the point (x, y) is equidistant from the points (-2, 8) and (-3, -5).
Answer:
Let A (- 2, 8), B (- 3, – 5) and P (x, y). If P is equidistant from A, B, then PA = PB.
Distance formula =
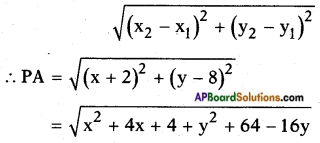

Squaring on both sides we get, x2 + y2 + 4x – 16y + 68
= x2 + y2 + 6x +10y + 34
⇒ 4x – 16y – 6x – 10y = 34-68
⇒ – 2x – 26y = -34
⇒ x + 13y = 17 is the required condition.