AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 8 Similar Triangles Ex 8.1 Textbook Questions and Answers.
AP State Syllabus SSC 10th Class Maths Solutions 8th Lesson Similar Triangles Exercise 8.1
10th Class Maths 8th Lesson Similar Triangles Ex 8.1 Textbook Questions and Answers
Question 1.
In △PQR, ST is a line such that \(\frac{PS}{SQ}\) = \(\frac{PT}{TR}\) and also ∠PST = ∠PRQ.
Prove that △PQR is an isosceles triangle.
Answer:
Given : In △PQR,
\(\frac{PS}{SQ}\) = \(\frac{PT}{TR}\) and ∠PST= ∠PRQ.
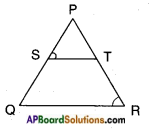
R.T.P: △PQR is isosceles.
Proof: \(\frac{PS}{SQ}\) = \(\frac{PT}{TR}\)
Hence, ST || QR (Converse of Basic proportionality theorem)
∠PST = ∠PQR …….. (1)
(Corresponding angles for the lines ST || QR)
Also, ∠PST = ∠PRQ ……… (2) given
From (1) and (2),
∠PQR = ∠PRQ
i.e., PR = PQ
[∵ In a triangle sides opposite to equal angles are equal]
Hence, APQR is an isosceles triangle.
![]()
Question 2.
In the given figure, LM || CM and LN || CD. Prove that \(\frac{AM}{AB}\) = \(\frac{AN}{AD}\).
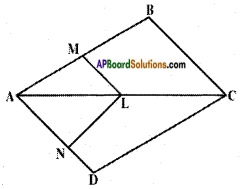
Answer:
Given : LM || CB and LN || CD In △ABC, LM || BC (given) Hence,

Adding ‘1’ on both sides.
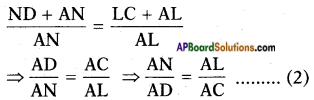
From (1) and (2)
∴ \(\frac{AM}{AB}\) = \(\frac{AN}{AD}\).
Question 3.
In the given figure, DE || AC and DF || AE. Prove that \(\frac{BF}{FE}\) = \(\frac{BE}{AC}\).
Answer:
In △ABC, DE || AC
Hence \(\frac{BE}{EC}\) = \(\frac{BD}{DA}\) ………. (1)
[∵ A line drawn parallel to one side of a triangle divides the other two sides in the same ratio – Basic proportionality theorem]
Also in △ABE, DF || AE
Hence \(\frac{BF}{FE}\) = \(\frac{BD}{DA}\) ………. (2)
From (1) and (2), \(\frac{BF}{FE}\) = \(\frac{BE}{AC}\) Hence proved.
![]()
Question 4.
Prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side (Using Basic proportionality theorem).
Answer:
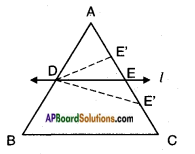
Given: In △ABC; D is the mid-point of AB.
A line ‘l’ through D, parallel to BC, meeting AC at E.
R.T.P: E is the midpoint of AC.
Proof:
DE || BC (Given)
then
\(\frac{AD}{DB}\) = \(\frac{AE}{EC}\)(From Basic Proportional theorem)
Also given ‘D’ is mid point of AB.
Then AD = DB.
⇒ \(\frac{AD}{DB}\) = \(\frac{DB}{DB}\) = \(\frac{AE}{EC}\) = 1
⇒ AE = EC
∴ ‘E’ is mid point of AC
∴ The line bisects the third side \(\overline{\mathrm{AC}}\).
Hence proved.
Question 5.
Prove that a line joining the mid points of any two sides of a triangle is parallel to the third side. (Using converse of Basic proportionality theorem)
Answer:
Given: △ABC, D is the midpoint of AB and E is the midpoint of AC.
R.T.P : DE || BC.
Proof:
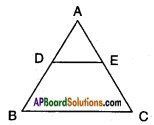
Since D is the midpoint of AB, we have AD = DB ⇒ \(\frac{AD}{DB}\) = 1 ……. (1)
also ‘E’ is the midpoint of AC, we have AE = EC ⇒ \(\frac{AE}{EC}\) = 1 ……. (2)
From (1) and (2)
\(\frac{AD}{DB}\) = \(\frac{AE}{EC}\)
If a line divides any two sides of a triangle in the same ratio then it is parallel to the third side.
∴ DE || BC by Basic proportionality theorem.
Hence proved.
![]()
Question 6.
In the given figure, DE || OQ and DF || OR. Show that EF || QR.
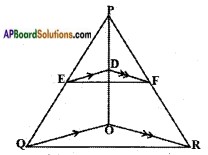
Answer:
Given: △PQR, DE || OQ; DF || OR
R.T.P: EF || QR
Proof:
In △POQ;
\(\frac{PE}{EQ}\) = \(\frac{PD}{DO}\) ……. (1)
[∵ ED || QO, Basic proportionality theorem]
In △POR; \(\frac{PF}{FR}\) = \(\frac{PD}{DO}\) ……. (2) [∵ DF || OR, Basic Proportionality Theorem]
From (1) and (2),
\(\frac{PE}{EQ}\) = \(\frac{PF}{FR}\)
Thus the line \(\overline{\mathrm{EF}}\) divides the two sides PQ and PR of △PQR in the same ratio.
Hence, EF || QR. [∵ Converse of Basic proportionality theorem]
Question 7.
In the given figure A, B and C are points on OP, OQ and OR respec¬tively such that AB || PQ and AC || PR. Show that BC || QR.
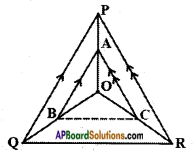
Answer:
Given:
In △PQR, AB || PQ; AC || PR
R.T.P : BC || QR
Proof: In △POQ; AB || PQ
\(\frac{OA}{AP}\) = \(\frac{OB}{BQ}\) ……… (1)
(∵ Basic Proportional theorem)
and in △OPR, Proof: In △POQ; AB || PQ
\(\frac{OA}{AP}\) = \(\frac{OC}{CR}\) ……… (2)
From (1) and (2), we can write
\(\frac{OB}{BQ}\) = \(\frac{OC}{CR}\)
Then consider above condition in △OQR then from (3) it is clear.
∴ BC || QR [∵ from converse of Basic Proportionality Theorem]
Hence proved.
![]()
Question 8.
ABCD is a trapezium in which AB || DC and its diagonals intersect each other at point ‘O’. Show that\(\frac{AO}{BO}\) = \(\frac{CO}{DO}\).
Answer:
Given: In trapezium □ ABCD, AB || CD. Diagonals AC, BD intersect at O.
R.T.P: \(\frac{AO}{BO}\) = \(\frac{CO}{DO}\)
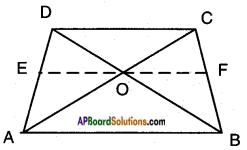
Construction:
Draw a line EF passing through the point ‘O’ and parallel to CD and AB.
Proof: In △ACD, EO || CD
∴ \(\frac{AO}{CO}\) = \(\frac{AE}{DE}\) …….. (1)
[∵ line drawn parallel to one side of a triangle divides other two sides in the same ratio by Basic proportionality theorem]
In △ABD, EO || AB
Hence, \(\frac{DE}{AE}\) = \(\frac{DO}{BO}\)
[∵ Basic proportionality theorem]
\(\frac{BO}{DO}\) = \(\frac{AE}{ED}\) …….. (2) [∵ Invertendo]
From (1) and (2),
\(\frac{AO}{CO}\) = \(\frac{BO}{DO}\)
⇒ \(\frac{AO}{BO}\) = \(\frac{CO}{DO}\) [∵ Alternendo]
![]()
Question 9.
Draw a line segment of length 7.2 cm and divide it in the ratio 5 : 3. Measure the two parts.
Answer:
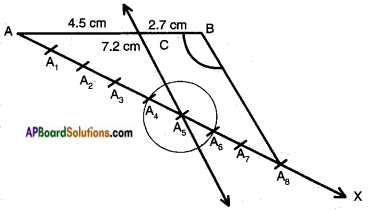
Steps of construction:
- Draw a line segment \(\overline{\mathrm{AB}}\) of length 7.2 cm.
- Construct an acute angle ∠BAX at A.
- Mark off 5 + 3 = 8 equal parts (A1, A2, …., A8) on \(\stackrel{\leftrightarrow}{\mathrm{AX}}\) with same radius.
- Join A8 and B.
- Draw a line parallel to \(\stackrel{\leftrightarrow}{\mathrm{A}_{8} \mathrm{~B}}\) at A5 meeting AB at C.
- Now the point C divides AB in the ratio 5:3.
- Measure AC and BC. AC = 4.5 cm and BC = 2.7 cm.