AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 11 Trigonometry Ex 11.4 Textbook Questions and Answers.
AP State Syllabus SSC 10th Class Maths Solutions 11th Lesson Trigonometry Exercise 11.4
10th Class Maths 11th Lesson Trigonometry Ex 11.4 Textbook Questions and Answers
Question 1.
Evaluate the following:
i) (1 + tan θ + sec θ) (1 + cot θ – cosec θ)
Answer:
Given (1 + tan θ + sec θ) (1 + cot θ – cosec θ)
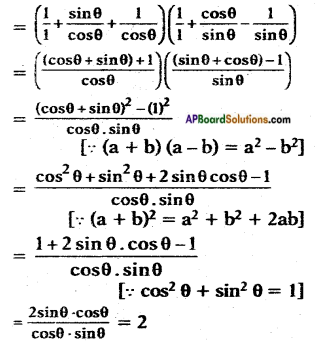
ii) (sin θ + cos θ)2 + (sin θ – cos θ)2
Answer:
Given (sin θ + cos θ)2 + (sin θ – cos θ)2
= (sin2 θ + cos2 θ + 2 sin θ cos θ) + (sin2 θ + cos2 θ – 2 sin θ cos θ) [∵ (a + b)2 = a2 + b2 + 2ab
(a – b)2 = a2 + b2 – 2ab]
= 1 + 2 sin θ cos θ + 1 – 2 sin θ cos θ [∵ sin2 θ + cos2 θ = 1]
= 1 + 1
= 2
iii) (sec2 θ – 1) (cosec2 θ – 1)
Answer:
Given (sec2 θ – 1) (cosec2 θ – 1)
= tan2 θ × cot2 θ [∵ sec2 θ – tan2 θ = 1; cosec2 θ – cot2 θ = 1]
= tan2 θ × \(\frac{1}{\tan ^{2} \theta}\) = 1
![]()
Question 2.
Show that (cosec θ – cot θ)2 = \(\frac{1-\cos \theta}{1+\cos \theta}\)
Answer:
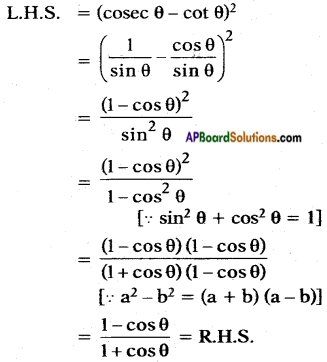
Question 3.
Show that \(\sqrt{\frac{1+\sin A}{1-\sin A}}\) = sec A + tan A
Answer:
Given that L.H.S. = \(\sqrt{\frac{1+\sin A}{1-\sin A}}\)
Rationalise the denominator, rational factor of 1 – sin A is 1 + sin A.
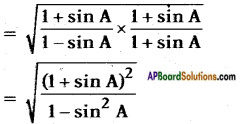
[∵ (a + b)(a + b) = (a + b)2]; (a – b)(a + b) = a2 — b2]
= \(\sqrt{\frac{(1+\sin A)^{2}}{\cos ^{2} A}}\)
= \(\frac{1+\sin A}{\cos A}\)
= \(\frac{1}{\cos A}+\frac{\sin A}{\cos A}\)
= sec A + tan A = R.H.S.
![]()
Question 4.
Show that \(\frac{1-\tan ^{2} A}{\cot ^{2} A-1}\) = tan2 A
Answer:

Question 5.
Show that \(\frac{1}{\cos \theta}\) – cos θ = tan θ – sin θ.
Answer:
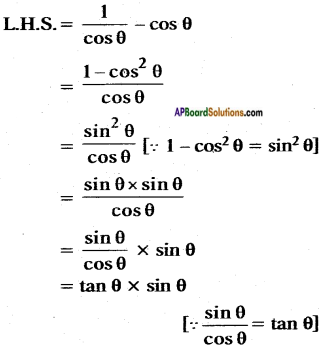
![]()
Question 6.
Simplify sec A (1 – sin A) (sec A + tan A)
Answer:
L.H.S. = sec A (1 – sin A) (sec A + tan A)
= (sec A – sec A . sin A) (sec A + tan A)
= (sec A – \(\frac{1}{\cos A}\) . sin A) (sec A + tan A)
= (sec A – tan A) (sec A + tan A)
= sec2 A – tan2 A [∵ sec2 A – tan2 A = 1]
= 1
Question 7.
Prove that (sin A + cosec A)2 + (cos A + sec A)2 = 7 + tan2 A + cot2 A
Answer:
L.H.S. = (sin A + cosec A)2 + (cos A + sec A)2
= (sin2 A + cosec2 A + 2 sin A . cosec A) + (cos2 A – sec2 A + 2 cos A . sec A) [∵ (a + b)2 = a2 + b2 + 2ab]
= (sin2 A + cos2 A) + cosec2 A + 2 sin A . \(\frac{1}{\sin A}\) + sec2 A + 2 cos A . \(\frac{1}{\cos A}\)
[∵ \(\frac{1}{\sin A}\) = cosec A; \(\frac{1}{\cos A}\) = sec A]
= 1 +(1 + cot2 A) + 2 + (1 + tan2 A) + 2
[∵ sin2 A + cos2 A = 1; cosec2 A = 1 + cot2 A; sec2 A = 1 + tan2 A]
= 7 + tan2 A + cot2 A
= R.H.S.
Question 8.
Simplify (1 – cos θ) (1 + cos θ) (1 + cot2 θ)
Answer:
Given that
(1 – cos θ) (1 + cos θ) (1 + cot2 θ)
= (1 – cos2 θ) (1 + cot2 θ)
[∵ (a – b) (a + b) = a2 – b2]
= sin2 θ. cosec2 θ [∵ 1 – cos2 θ = sin2 θ; 1 + cot2 θ = cosec2 θ]
= sin2 θ . \(\frac{1}{\sin ^{2} \theta}\) [∵ cosec θ = \(\frac{1}{\sin \theta}\)]
= 1
![]()
Question 9.
If sec θ + tan θ = p, then what is the value of sec θ – tan θ?
Answer:
Given that sec θ + tan θ = p ,
We know that sec2 θ – tan2 θ = 1
sec2 θ – tan2 θ = (sec θ + tan θ) (sec θ – tan θ)
= p (sec θ – tan θ)
= 1 (from given)
⇒ sec θ – tan θ = \(\frac{1}{p}\)
Question 10.
If cosec θ + cot θ = k, then prove that cos θ = \(\frac{k^{2}-1}{k^{2}+1}\)
Answer:
Method-I:
Given that cosec θ + cot θ = k
R.H.S. = \(\frac{k^{2}-1}{k^{2}+1}\)
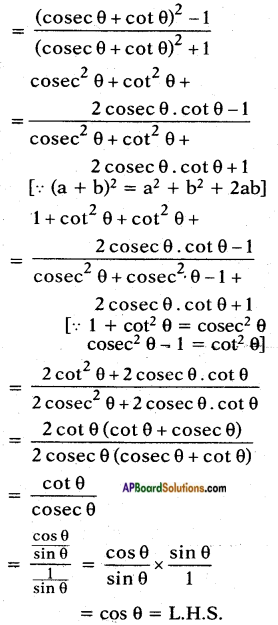
![]()
Method – II:
Given that cosec θ + cot θ = k ……..(1)
We know that cosec2 θ – cot2 θ = 1
⇒ (cosec θ + cot θ) (cosec θ – cot θ) = 1 [∵ a2 – b2 = (a -b)(a + b)]
⇒ k (cosec θ – cot θ) = 1
⇒ (cosec θ – cot θ) = \(\frac{1}{k}\)
By solving (1) and (2)

According to identity cos2 θ + sin2 θ = 1
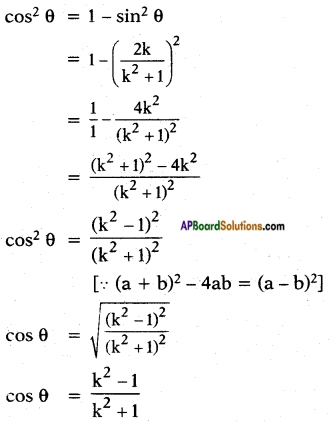
Hence proved.