AP State Syllabus SSC 10th Class Maths Solutions 8th Lesson Similar Triangles Optional Exercise
AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 8 Similar Triangles Optional Exercise Textbook Questions and Answers.
10th Class Maths 8th Lesson Coordinate Geometry Optional Exercise Textbook Questions and Answers
Question 1.
In the given figure, \(\frac{QT}{PR}\) = \(\frac{QR}{QS}\) and ∠1 = ∠2. Prove that △PQS ~ △TQR.
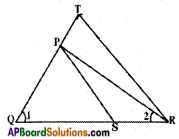
Answer:
Given: \(\frac{QT}{PR}\) = \(\frac{QR}{QS}\)
∠1 = ∠2
R.T.P : △PQS ~ △TQR
Proof: In △PQR; ∠1 = ∠2 Thus, PQ = PR
[∵ sides opp. to equal angles are equal]
\(\frac{QT}{PR}\) = \(\frac{QR}{QS}\) ⇒ \(\frac{QT}{PQ}\) = \(\frac{QR}{QS}\)
i.e., the line PS divides the two sides QT and QR of △TQR in the same ratio.
Hence, PS // TR.
[∵ If a line join of any two points on any two sides of triangle divides the two sides in the same ratio, then the line is parallel to the third side]
Hence, PS // TR (converse of B.P.T)
Now in △PQS and △TQR
∠QPS = ∠QTR
[∵ ∠P, ∠T are corresponding angles for PS // TR]
∠QSP = ∠QRT
[∵ ∠S, ∠R are corresponding angles for PS // TR]
∠Q = ∠Q (common)
∴ △PQS ~ △TQR (by AAA similarity)
![]()
Question 2.
Ravi is 1.82 m tall. He wants to find the height of a tree in his backyard. From the tree’s base he walked 12.20 m. along the tree’s shadow to a position where the end of his shadow exactly overlaps the end of the tree’s shadow. He is now 6.10 m from the end of the shadow. How tall is the tree?
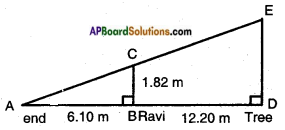
Answer:
Given:
Height of Ravi ‘BC’ = 1.82 m.
Distance of Ravi from the foot of the tree BD = 12.2 m.
Length of the shadow of Ravi = AB = 6.10 m
Let DE represent the tree.
From the figure, △ABC ~ △ADE.
Thus, \(\frac{AB}{AD}\) = \(\frac{BC}{DE}\) = \(\frac{AC}{AE}\)
Ratio of corresponding sides of two similar triangles are equal]
\(\frac{6.10}{6.10+12.20}\) = \(\frac{1.82}{\mathrm{DE}}\)
DE = \(\frac{1.82 \times 18.30}{6.10}\) = 5.46 m
Thus the height of the tree = 5.46 m.
Question 3.
The diagonal AC of a parallelogram ABCD intersects DP at the point Q, where ‘P’ is any point on side AB. Prove that CQ × PQ = QA × QD.
Answer:
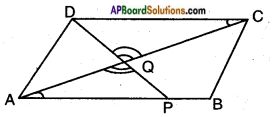
Given: □ ABCD is a parallelogram.
P is a point on AB.
DP and AC intersect at Q.
R.T.P.: CQ . PQ = QA . QD.
Proof: In △CQD, △AQP
∠QCD = ∠QAP
∠CQD = ∠AQP
∴ ∠QDC = ∠QPA
(∵ Angle sum property of triangles)
Thus, △CQD ~ △AQP by AAA similarity condition.
\(\frac{CQ}{AQ}\) = \(\frac{QD}{QP}\) = \(\frac{CD}{AP}\)
[∵ Ratio of corresponding sides of similar triangles are equal]
\(\frac{CQ}{AQ}\) = \(\frac{QD}{QP}\)
CQ . PQ = QA . QD [Q.E.D]
![]()
Question 4.
△ABC and △AMP are two right triangles right angled at B and M respectively. Prove that (i) △ABC ~ △AMP (ii) \(\frac{CA}{PA}\) = \(\frac{BC}{MP}\)
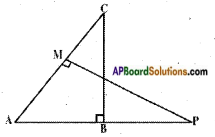
Answer:
Given: △ABC; ∠B = 90°
AAMP; ∠M = 90°
R.T.P : i) △ABC ~ △AMP
Proof: In △ABC and △AMP
∠B = ∠M [each 90° given]
∠A = ∠A [common]
Hence, ∠C = ∠P
[∵ Angle sum property of triangles]
∴ △ABC ~ △AMP (by A.A.A. similarity)
ii) △ABC ~ △AMP (already proved)
\(\frac{AB}{AM}\) = \(\frac{BC}{MP}\) = \(\frac{CA}{PA}\)
[∵ Ratio of corresponding sides of similar triangles are equal]
\(\frac{CA}{PA}\) = \(\frac{BC}{MP}\)
Question 5.
An aeroplane leaves an airport and flies due north at a speed of 1000 kmph. At the same time another aeroplane leaves the same airport and flies due west at a speed of 1200 kmph. How far apart will the two planes be after 1\(\frac{1}{2}\) hour?
Answer:
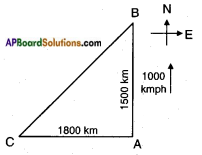
Given: Speed of the first plane due north = 1000 kmph.
Speed of the second plane due west = 1200 kmph.
Distance = Speed × Time
Distance travelled by the first plane in
1\(\frac{1}{2}\) hrs = 1000 × 1\(\frac{1}{2}\) = 1000 × \(\frac{3}{2}\) = 1500 km.
Distance travelled by the second plane
in 1\(\frac{1}{2}\) hrs = 1200 × \(\frac{3}{2}\) = 1800 km.
From the figure, △ABC is a right triangle; ∠A = 90°.
AB2 + AC2 = BC2
[Pythagoras theorem]
15002 + 18002 = BC2
2250000 + 3240000 = BC2
∴ BC = √5490000
= 100 × √549 m
≅ 100 × 23.43
≅ 2243km.
![]()
Question 6.
In a right triangle ABC right angled at C. P and Q are points on sides AC and CB respectively which divide these sides in the ratio of 2:1. Prove that
i) 9AQ2 = 9AC2 + 4BC2
ii) 9BP2 = 9BC2 + 4AC2
iii) 9(AQ2 + BP2) = 13AB2
Answer:
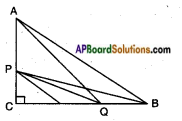
Given: In △ABC; ∠C = 90°
R.T.P.: i) 9AQ2 = 9AC2 + 4BC2
Proof: In △ACQ; ∠C = 90°
AC2 + CQ2 = AQ2
[side2 + side2 = hypotenuse2]
AQ2 = AC2 + \(\left(\frac{2}{3} \mathrm{BC}\right)^{2}\)
[∵ Q divides CB in the ratio 2 : 1
CQ = \(\frac{2}{3}\)BC]
AQ2 = AC2 + \(\frac{4}{9} \mathrm{BC}^{2}\)
AQ2 = \(\frac{9 \mathrm{AC}^{2}+4 \mathrm{BC}^{2}}{9}\)
⇒ 9AQ2 = 9AC2 + 4BC2
ii) 9BP2 = 9BC2 + 4AC2
Proof: In △PCB,
PB2 = PC2 + BC2 [Pythagoras theorem]

⇒ PB2 = AC2 + 9BC2
[!! If we take P on CA, in the ratio 2 : 1 then we get
BP2 = PC2 + BC2
BP2 = \(\left(\frac{2}{3} \mathrm{A}\right)^{2}\) + BC2
BP2 = \(\frac{4}{9} \mathrm{AC}^{2}\) + BC2
BP2 = \(\frac{4 \mathrm{AC}^{2}+9 \mathrm{BC}^{2}}{9}\)
9BP2 = 4AC2 + 9BC2
![]()
iii) 9 (AQ2 + BP2) = 13 AB2
Proof: In △ABC,
AC2 + BC2 = AB2
[Pythagoras theorem]
Also, from (i) and (ii),
