Use these Inter 1st Year Maths 1A Formulas PDF Chapter 3 Matrices to solve questions creatively.
Intermediate 1st Year Maths 1A Matrices Formulas
→ An ordered rectangular array of elements is called a matrix.
→ A matrix in which the number of rows is equal to the number of columns, is called a square matrix. Otherwise, it is called a rectangular matrix. In a square matrix, an element aij is in principal diagonal, if i = j
→ If each non-diagonal element of a square matrix is equal to zero, then it is called a diagonal matrix.
→ If each non-diagonal element of a square matrix is equal to zero and each diagonal element is equal to a scalar, then it is called a scalar matrix.
→ If each non-diagonal element of a square matrix is equal to zero and each diagonal element is equal to 1, then that matrix is called a unit matrix or Identity matrix.
→ If A is a square matrix then the sum of elements in the principal diagonal of A is called the trace of A.
- Matrix addition is commutative.
- Matrix addition is associative.
- Matrix multiplication is associative.
- Matrix multiplication is distributive over matrix addition.
![]()
→ A square matrix A is said to be an idempotent matrix if A2 = A.
→ A square matrix A is said to be an involuntary matrix if A2 = I.
→ A square matrix A is said to be a nilpotent matrix, if there exist a positive integer n such that An = 0. If n is the least positive integer such thatAn = 0, then n is called index of the nilpotent matrix A.
→ The matrix obtained by interchanging rows and columns is called transpose of the given matrix. Transpose of A is denoted by AT (or) A’.
→ For any matrices A and B
- (AT)T = A
- (A + B)T = AT + BT (A and B are same order)
- (AB)T = BTAT. (If A and B are of orders m xn and n xp respectively)
→ A square matrix A is said to be symmetric if AT = A.
→ A square matrix A is said to be skew symmetric if AT = A.
→ Every square matrix can be uniquely expressed as a sum of symmetric matrix and a skew symmetric matrix.
→ The minor of an element in the square matrix of order ‘3’ is defined as the determinant of 2 × 2 matrix, obtained after deleting the row and the column in which the element is present.
→ The cofactor of an element in the ith row and jth column of 3 × 3 matrix is defined as its minor multiplied by (-1)i+j.
→ The sum of the products of the elements of any row or column with their corresponding cofactors is called the determinant of a matrix.
- A square ‘A’ is said to be a singular matrix if det A = 0.
- A square A’ is said to be a non-singular matrix if det A ≠ 0.
→ The transpose of the matrix obtained by replacing.the elements of a square matrix A by the corresponding cofactors is called the adjoint matrix of A and it is denoted by adj (A).
- A square matrix ‘A is said to be an invertible matrix if there exists a square matrix B such that AB = BA = I the matrix B is called inverse of A and it is denoted by A-1.
- If A is an invertible then A-1 = 1.
→ A square matrix A is non-singular if A is invertible.
- If A and B are non-singular matrices of same type then Adj (AB) = (Adj B) (Adj A).
- If A is a square matrix of type n then det (Adj A) = (det A)n-1.
→ A matrix obtained by deleting some rows or columns (or both) of a matrix is called a submatrix.
→ Let Abe a non-zero matrix, the rank of A is defined as the maximum of the orders of the non-singular square submatrices of A. The rank of a null matrix is zero. The rank of a matrix A is denoted as rank (A) or P (A).
→ A system of linear equations is
- Consistent, if it has a solution
- Inconsistent, if it has no solution
→ Non homogeneous system
- a1x + b1y + c1z = d1
- a2x + b2y + c2z = d2
- a3x + b3y + c3z = d3
![]()
→ The above system of equations has
- aunique solution if rank (A) = Rank [AD] = 3
- infinity many solutions, if rank (A) = Rank ([AD]) < 3
- no solution, if rank A ≠ Rank ([AD])
→ Homogeneous system of equations
- a1x + b1y + c1z = d1
- a2x + b2y + c2z = d2
- a3x + b3y + c3z = d3
→ The above system has
- Trival solution x = y = z = 0 only if rank (A) = 3
- infinitely many non-trival solutions if rank (A) < 3.
→ A matrix is an arrangement of real or complex numbers into rows and columns so that all the rows (columns) contain equal no. of elements.
→ If a matrix consists of ‘m’ rows and ‘n’ columns, then it is said to be of order m × n.
→ A matrix of order n × n is said to be a square matrix of order n.
→ A matrix (aij)m×n is said to be a null matrix if aij = 0 for all i and j.
→ Two matrices of the same order are said to be equal if the corresponding elements in the matrices are all equal.
→ A matrix (aij)n×n is a diagonal matrix aij = 0 for all i ≠ j
→ A matrix (aij)n×n is a scalar matrix if a = 0 for all i ≠ j and aij = k (constant) for i = j
→ A matrix (aij)n×n is said to be a unit matrix of order n, denoted by In if aij = 1, when i = j and aij = 0 when i ≠ j
Ex: I2 = \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)
I3 = \(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\)
→ If A = (aij)m×n, B = (bij)m×n, then A + B = (aij + bij)m×n
→ Matrix addition is commutative and associative
→ Matrix multiplication is not commutative but associative
→ If A is a matrix of order m × n, then AIn = ImA = A(AI = IA = A)
→ If AB = CA = I, then B = C
![]()
→ If A = (aij)m×n, then A T = (aij)n×m
→ (KA)T = KAT, (A + B)T = AT + BT, (AB)T = BT.AT
→ A(B + C) = AB + AC, (A + B)C = AC + BC
→ A square matrix is said to be “non-singular” if detA ≠ 0
→ A square matrix is said to be “singular” if detA = 0
→ If AB = 0, where A and B are non-zero square matrices, then both A are singular.
→ A minor of any element in a square matrix is determinant of the matrix obtained by omitting the row and column in which the element is present.
→ In (aij)n×n, the cofactor of aij is (-1)i+j × (minor of aij).
→ In a square matrix, the sum of the products of the elements of any row (column) and the corresponding cofactors is equal to the determinant of the matrix.
→ In a square matrix, the sum of the products of the elements of any row (column) and the corresponding cofactors of any other row (column) is alway s zero.
→ If A is any square matrix, then A adjA = adjA. A = detA. I
→ If A is any square matrix and there exists a matrix B such that AB = BA = I, then B is called the inverse of A and denoted by A-1.
→ AA-1 = A-1A = I.
→ If A is non-singular, then A-1 = \(\frac{{adj} A}{{det} A}\) (or) adj A = |A|AA-1
→ If A = \(\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right)\), then A-1 = \(\frac{1}{a d-b c}\left(\begin{array}{cc}
d & -b \\
-c & a
\end{array}\right)\)
→ (A-1)-1 = A, (AB)-1 = B-1.A-1, (A-1)T =( AT)-1; (ABC….)-1 = C-1B-1A-1.
Theorem:
Matrix multiplication is associative. i.e. if conformability is assured for the matrices A, B and C, then (AB)C = A(BC).
Proof:

![]()
Theorem:
Matrix multiplication is distributive over matrix addition i.e. if conformability is assured for the matrices A, B and C, then
(i) A (B + C) = AB + AC
(ii) (B + C) A = BA + CA
Proof:
Let A = (aij)m×n, B = (bjk)n×p C = (cki)n×p
B + C = (djk)n×p, where djk = bjk + cjk
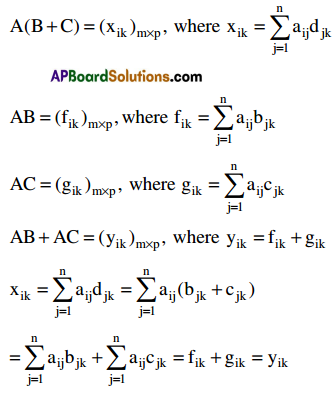
∴ A(B + C) = AB + AC
Similarly we can prove that
(B + C) = BA + CA.
Theorem:
If A is any matrix, then (AT)T = A.
Proof:
Let A = (aij)m×n
AT = (a’jk)n×m, where a’ji = aij
(AT)T = (a”ji)m×n, where a”ij = aji
a”ij = a’ji = aij
∴ (AT)T = A
Theorem:
If A and B are two matrices o same type, then (A + B)T = AT + BT.
Proof:
Let A = (aij)m×n, B = (bij)
A + B = (cij)m×n,where cij = aij + bij
(A + B)T = (c’ji)n×m. c’ji = cij
AT = (a’ji)n×m,where a’ji = aij
BT = (bji)n×m. where. b’kj = bjk
AT + BT = (dji)n×m, where dji = a’ji + b’ji
c’ji = cij = aij + bij = a’ji + b’ji = dji
∴(A + B)T = AT + BT
Theorem:
If A and B are two matrices for which conformability for multiplication is assured, then (AB)T = BTAT.
Pr0of:
Let A = (aij)m×n, B = (bji)n×p
AB = (cik)m×p, where cik = \(\sum_{j=1}^{n}\) aijbjk
(AB)T = (cki)p×m,where cki = cik
AT = (aji)n×m,where aji = aij
BT = (bkj)p×n, where bkj = bjk
BT . AT = (dki )p×m, where dki= \(\sum_{j=1}^{n}\) bkjaji
c’ki = cik = \(\sum_{j=1}^{n}\) aijbjk= \(\sum_{j=1}^{n}\) bkjajidki
∴ (AB)T = BTAT
![]()
Theorem:
If A and B are two invertible matrices of same type then AB is also invertible and (AB)-1 = B-1A-1.
Proof:
A is invertible matrix ⇒ A-1 exists and AA-1 = A-1A = I.
B is an invertible matrix ⇒ B-1 exists and
BB-1 = B-1B = I
Now (AB)(B-1A-1) = A(BB-1)A-1 = AIA-1 = AA-1 = I
(B-1A-1)(AB) = B-1(A-1A)B ∴ AB is invertible and
= B-1IB = B-1B = I
(AB)(B-1A-1) = (B-1A-1) = (B-1A-1)(AB) = 1
(AB)-1 = B-1A-1.
Theorem:
If A is a non-singular matrix then A is invertible and A-1 = \(\frac{{Adj} A}{{det} A}\).
Proof:
Let A = \(\left[\begin{array}{lll}
\mathrm{a}_{1} & \mathrm{~b}_{1} & \mathrm{c}_{1} \\
\mathrm{a}_{2} & \mathrm{~b}_{2} & \mathrm{c}_{2} \\
\mathrm{a}_{3} & \mathrm{~b}_{3} & \mathrm{c}_{3}
\end{array}\right]\) be a non – singular matrix.
∴ det A ≠ 0
