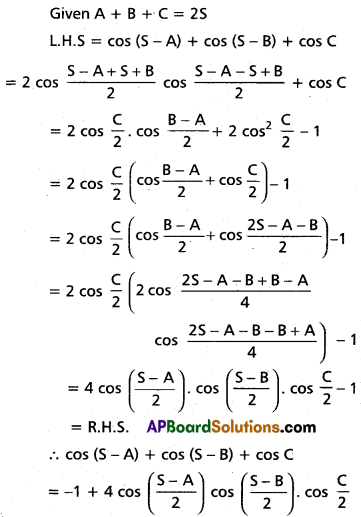Inter 1st Year Maths 1A Trigonometric Ratios up to Transformations Solutions Ex 6(f)

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Trigonometric Ratios up to Transformations Solutions Exercise 6(f) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Trigonometric Ratios up to Transformations Solutions Exercise 6(f)

Question 1.
If A, B, C are angles in a triangle, then prove that
(i) sin 2A – sin 2B + sin 2C = 4 cos A sin B cos C
Solution:
∵ A, B, C are angles in a triangle
⇒ A + B + C = 180° ……….(1)
LHS = sin 2A – sin 2B + sin 2C
= sin 2A + sin 2C – sin 2B
= 2 sin (\(\frac{2 A+2 C}{2}\)) . cos(\(\frac{2 A-2 C}{2}\)) – sin 2B
= 2 sin (A + C) cos (A – C) – sin B
= 2 sin (180° – B) cos (A – C) – 2 sin B cos B
= 2 sin B cos (A – C) – 2 sin B cos B
= 2 sin B [cos (A – C) – cos B]
= 2 sin B [cos (A – C) – cos (180° – (A + C)]
= 2 sin B [cos (A – C) + cos (A + C)]
= 2 sin B (2 cos A cos C)
= 4 cos A sin B cos C
∴ sin 2A – sin 2B + sin 2C = 4 cos A sin B cos C

(ii) cos 2A – cos 2B + cos 2C = 1 – 4 sin A cos B Sin C
Solution:
L.H.S. = -(cos 2B – cos 2A) + cos 2C
= -2 sin (A + B) sin (A – B) + cos 2C
= -2 sin (180° – C) sin (A – B) + cos 2C
= -2 sin C sin (A – B) + 1 – 2 sin2C
= 1 – 2 sin C (sin (A – B) + sin C)
= 1 – 2 sin C sin (A – B) + sin (180° – \(\overline{\mathrm{A}+\mathrm{B}}\))
= 1 – 2 sin C (sin (A – B) + sin (A + B))
= 1 – 2 sin C (2 sin A cos B)
= 1 – 4 sin A cos B sin C
= R.H.S.

Question 2.
If A, B, C are angles in a triangle, then prove that
(i) sin A + sin B – sin C = 4 sin \(\frac{A}{2}\) sin \(\frac{B}{2}\) cos \(\frac{C}{2}\)
Solution:
L.H.S. = (sin A + sin B) – sin C
= 2 sin (\(\frac{A+B}{2}\)) cos (\(\frac{A-B}{2}\)) – sin C
Inter 1st Year Maths 1A Trigonometric Ratios up to Transformations Solutions Ex 6(f) Q2(i)

(ii) cos A + cos B – cos C = -1 + 4 cos \(\frac{A}{2}\) cos \(\frac{B}{2}\) sin \(\frac{C}{2}\)
Solution:
A, B, C are angles in a triangle
A + B + C = 180° ………(1)
LHS = cos A + cos B – cos C
Inter 1st Year Maths 1A Trigonometric Ratios up to Transformations Solutions Ex 6(f) Q2(ii)

Question 3.
If A, B, C are angles in a triangle, then prove that
(i) sin²A + sin²B – sin²C = 2 sin A sin B cos C
Solution:
Given A + B + C = 180°
L.H.S. = sin²A + [sin²B – sin²C]
= sin²A + sin (B + C) sin (B – C)
= sin²A + sin (180° – A) . sin (B – C)
= sin²A + sin A . sin (B – C)
= sin A (sin A + sin (B – C))
= sin A [sin (180° – \(\overline{\mathrm{B}+\mathrm{C}}\)) + sin (B – C)]
= sin A [sin (B + C) + sin (B – C)]
= sin A [2 sin B cos C]
= 2 sin A sin B cos C
= R.H.S

(ii) cos²A + cos²B – cos²C = 1 – 2 sin A sin B cos C
Solution:
A, B, C are angles in a triangle
⇒ A + B + C = 180° ……..(1)
L.H.S = cos²A + cos²B – cos²C
= cos²A + cos²B – cos²C
Inter 1st Year Maths 1A Trigonometric Ratios up to Transformations Solutions Ex 6(f) Q3(ii)
= 1 + cos (A + B) cos (A – B) – cos²C
= 1 + cos (180° – C) cos (A – B) – cos²C [By (1)]
= 1 – cos C cos (A – B) – cos²C
= 1 – cos C [cos (A – B) + cos C]
= 1 – cos C [cos (A – B) + cos(180° – \(\overline{A+B}\)] [By eq. (1)]
= 1 – cos C [cos (A – B) – cos (A + B)]
= 1 – cos C [2 sin A sin B]
= 1 – 2 sin A sin B cos C
∴ cos²A + cos²B – cos²C = 1 – 2 sin A sin B cos C

Question 4.
If A + B + C = π, then prove that
(i) \(\cos ^{2} \frac{A}{2}+\cos ^{2} \frac{B}{2}+\cos ^{2} \frac{C}{2}\) = \(2\left[1+\sin \frac{A}{2}+\sin \frac{B}{2} \sin \frac{C}{2}\right]\)
Solution:
Inter 1st Year Maths 1A Trigonometric Ratios up to Transformations Solutions Ex 6(f) Q4(i)

(ii) \(\cos ^{2} \frac{A}{2}+\cos ^{2} \frac{B}{2}-\cos ^{2} \frac{C}{2}=2 \cos \frac{A}{2}\) \(\cos \frac{B}{2} \sin \frac{C}{2}\)
Solution:
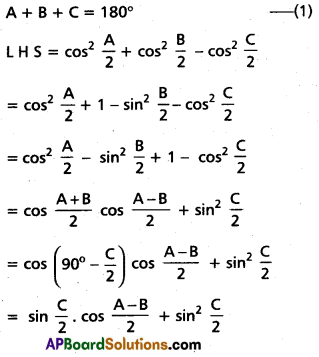
Inter 1st Year Maths 1A Trigonometric Ratios up to Transformations Solutions Ex 6(f) Q4(ii)

Question 5.
In triangle ABC, prove that
(i) \(\cos \frac{A}{2}+\cos \frac{B}{2}+\cos \frac{C}{2}\) = \(4 \cos \frac{\pi-A}{4} \cos \frac{\pi-B}{4} \cos \frac{\pi-C}{4}\)
Solution:
Inter 1st Year Maths 1A Trigonometric Ratios up to Transformations Solutions Ex 6(f) Q5(i)

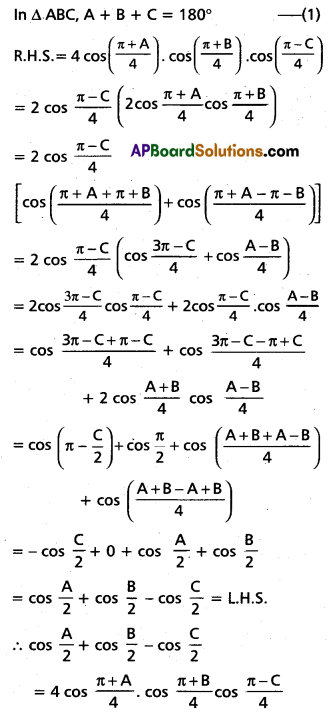
(ii) \(\cos \frac{A}{2}+\cos \frac{B}{2}-\cos \frac{C}{2}\) = \(4 \cos \frac{\pi+A}{4} \cdot \cos \frac{\pi+B}{4} \cos \frac{\pi-C}{4}\)
Solution:
Inter 1st Year Maths 1A Trigonometric Ratios up to Transformations Solutions Ex 6(f) Q5(ii)

(iii) \(\sin \frac{A}{2}+\sin \frac{B}{2}-\sin \frac{C}{2}\) = \(-1+4 \cos \frac{\pi-A}{4} \cos \frac{\pi-B}{4} \sin \frac{\pi-C}{4}\)
Solution:
Inter 1st Year Maths 1A Trigonometric Ratios up to Transformations Solutions Ex 6(f) Q5(iii)

Question 6.
If A + B + C = π/2, then prove that cos 2A + cos 2B + cos 2C = 1 + 4 sin A sin B sin C
Solution:
A + B + C = π/2 ………(1)
LHS = cos 2A + cos 2B + cos 2C
= 2 cos (\(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\)) cos (\(\frac{2 \mathrm{~A}-2 \mathrm{~B}}{2}\)) + cos 2C
= 2 cos (A + B) . cos (A – B) + cos 2C
= 2 cos (90° – C) cos (A – B) + cos 2C
= 2 sin C cos (A – B) + (1 – 2 sin²C)
= 1 + 2 sin C [cos (A – B) – sin C]
= 1 + 2 sin C [cos (A – B)- sin (90° – \(\overline{A+B}\))]
= 1 + 2 sin C [cos (A – B) – cos (A +B)]
= 1 + 2 sin C [2 sin A sin B]
= 1 + 4 sin A sin B sin C
= RHS
∴ cos 2A + cos 2B + cos 2C = 1 + 4 sin A sin B sin C

Question 7.
If A + B + C = 3π/2, then prove that
(i) cos²A + cos²B – cos²C = -2 cos A cos B sin C
Solution:
A + B + C = 3π/2 ……..(1)
L.H.S. = cos²A + cos²B – cos²C
= cos²A + (1 – sin²B) – cos²C
= (cos²A – sin²B) + (1 – cos²C)
= cos (A + B) cos (A – B) + sin²C
= cos (270° – C) cos(A – B) + sin²C
= -sin C cos (A – B) + sin²C
= sin C [sin C – cos (A – B)]
= sin C [sin (270°- \(\overline{A+B}\)) – cos (A – B)]
= sin C [-cos (A + B) – cos (A – B)]
= -sin C [cos (A + B) + cos (A – B)]
= -sin C [2 cos A cos B]
= -2 cos A cos B sin C
= RHS
∴ cos²A + cos²B – cos²C = -2 cos A cos B sin C

(ii) sin 2A + sin 2B – sin 2C = -4 sin A sin B cos C
Solution:
Here A + B + C = 270° ………(1)
LHS = sin 2A + sin 2B – sin 2C
= 2 sin (\(\frac{2 A+2 B}{2}\)) cos (\(\frac{2 A-2 B}{2}\)) – sin 2C
= 2 sin (A + B) . cos (A – B) – 2 sin C cos 2C
= 2 sin (270° – C) cos (A – B) – 2 sin C cos C
= -2 cos C cos (A – B) – 2 sin C cos C
= -2 cos C [cos (A – B) + sin C]
= -2 cos C [cos (A – B) + sin (270° – \(\overline{A+B}\))]
= -2 cos C [cos (A – B) – cos (A + B)]
= -2 cos C [2 sin A sin B]
= -4 sin A sin B cos C
= RHS
∴ sin 2A + sin 2B – sin 2C = -4 sin A sin B cos C

Question 8.
If A + B + C = 0°, then prove that
(i) sin 2A + sin 2B + sin 2C = -4 sin A sin B sin C
Solution:
Here A + B + C = 0 ………(1)
LHS = sin 2A + sin 2B + sin 2C
= 2 sin (\(\frac{2 A+2 B}{2}\)) cos (\(\frac{2 A-2 B}{2}\)) + sin 2C
= 2 sin (A + B) . cos (A – B) + 2 sin C cos 2C
= 2 sin (-C) cos (A – B) + 2 sin C cos C
= -2 sin C cos (A – B) + 2 sin C cos C
= -2 sin C [cos (A – B) – cos C]
= -2 sin C [cos (A – B) – cos (-A – B)]
= -2 sin C [cos (A – B) – cos (A + B)]
= -2 sin C [2 sin A sin B]
= -4 sin A sin B sin C
= RHS
∴ sin 2A + sin 2B + sin 2C = -4 sin A sin B sin C

(ii) sin A + sin B – sin C = – 4 cos \(\frac{A}{2}\) cos \(\frac{B}{2}\) sin \(\frac{C}{2}\)
Solution:
Inter 1st Year Maths 1A Trigonometric Ratios up to Transformations Solutions Ex 6(f) Q8(ii)

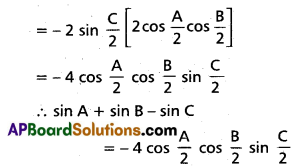
Question 9.
If A + B + C + D = 2π then prove that
(i) sin A – sin B + sin C – sin D = \(-4 \cos \left(\frac{A+B}{2}\right) \sin \left(\frac{A+C}{2}\right) \cos \left(\frac{A+D}{2}\right)\)
Solution:
Inter 1st Year Maths 1A Trigonometric Ratios up to Transformations Solutions Ex 6(f) Q9(i)

(ii) cos 2A + cos 2B + cos 2C + cos 2D = 4 cos (A + B) cos (A + C) cos (A + D)
Solution:
Inter 1st Year Maths 1A Trigonometric Ratios up to Transformations Solutions Ex 6(f) Q9(ii)

Question 10.
If A + B + C = 2S, then prove that
(i) sin (S – A) + sin (S – B) + sin C = \(4 \cos \left(\frac{S-A}{2}\right) \cos \left(\frac{S-B}{2}\right) \sin \frac{C}{2}\)
Solution:
Inter 1st Year Maths 1A Trigonometric Ratios up to Transformations Solutions Ex 6(f) Q10(i)

(ii) cos (S – A) + cos (S – B) + cos C = \(-1+4 \cos \left(\frac{S-A}{2}\right) \cos \left(\frac{S-B}{2}\right) \cdot \cos \frac{C}{2}\)
Solution:
Inter 1st Year Maths 1A Trigonometric Ratios up to Transformations Solutions Ex 6(f) Q10(ii)