Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Properties of Triangles Solutions Exercise 10(a) will help students to clear their doubts quickly.
Intermediate 1st Year Maths 1A Properties of Triangles Solutions Exercise 10(a)
All problems in this exercise refer to ΔABC
I.
Question 1.
Show that Σa(sin B – sin C) = 0
Solution:

Question 2.
If a = √3 + 1 cms, ∠B = 30°, ∠C = 45°, then find c.
Solution:
∠B = 30°, ∠C = 45° and a = (√3 + 1) cms
A = 180° – (B + C)
= 180° – (30° + 45°)
= 180° – 75°
= 105°
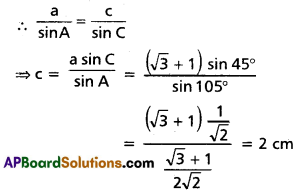
Question 3.
If a = 2 cms, b = 3 cms, c = 4 cms, then find cos A.
Solution:
a = 2 cms, b = 3 cms and c = 4 cms

Question 4.
If a = 26 cms, b = 30 cms and cos C = \(\frac{63}{65}\), then find c.
Solution:
a = 26 cms, b = 30 cms and cos C = \(\frac{63}{65}\)
c2 = a2 + b2 – 2ab cos C
⇒ c2 = 676 + 900 – 2 × 26 × 30 × \(\frac{63}{65}\)
⇒ c2 = 1576 – 1512
⇒ c2 = 64
⇒ c = 8
![]()
Question 5.
If the angles are in the ratio 1 : 5 : 6, then find the ratio of its sides.
Solution:
Given \(\frac{A}{1}=\frac{B}{5}=\frac{C}{6}\), B = 5A, C = 6A
A + B + C = 180°
⇒ A + 5A + 6A = 180°
⇒ 12A = 180°
⇒ A = 15°
∴ B = 5A = 75°
∴ C = 6A = 90°
a : b : c = sin A : sin B : sin C
= sin 15° : sin 75° : sin 90°
= \(\frac{\sqrt{3}-1}{2 \sqrt{2}}: \frac{\sqrt{3}+1}{2 \sqrt{2}}: 1\)
= (√3 – 1) : (√3 + 1) : 2√2
Question 6.
Prove that 2(bc cos A + ca cos B + ab cos C) = a2 + b2 + c2.
Solution:
L.H.S = Σ2bc cos A
= Σ2bc \(\frac{\left(b^{2}+c^{2}-a^{2}\right)}{2 b c}\)
= Σ(b2 + c2 – a2)
= b2 + c2 – a2 + c2 + a2 – b2 + a2 + b2 – c2
= a2 + b2 + c2
= R.H.S
Question 7.
Prove that \(\frac{a^{2}+b^{2}-c^{2}}{c^{2}+a^{2}-b^{2}}=\frac{\tan B}{\tan C}\)
Solution:
L.H.S = \(\frac{a^{2}+b^{2}-c^{2}}{c^{2}+a^{2}-b^{2}}=\frac{\tan B}{\tan C}\)
[∵ c2 = a2 + b2 – 2ab cos C and b2 = a2 + c2 – 2ac cos B]
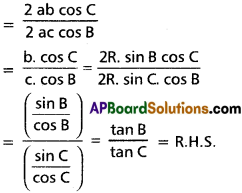
Question 8.
Prove that (b + c) cos A + (c + a) cos B + (a + b) cos C = a + b + c
Solution:
L.H.S = (b + c) cos A + (c + a) cos B + (a + b) cos C
= (b cos A + c cos A) + (c cos B + a cos B) + (a cos C + b cos C)
= (b cos C + c cos B) + (a cos C + c cos A) + (a cos B + b cos A)
= a + b + c
= R.H.S
Question 9.
Prove that (b – a cos C) sin A = a cos A sin C
Solution:
LHS = (b – a cos C) sin A
= (a cos C + c cos A – a cos C) sin A
= c cos A sin A [∵ b = a cos C + c cos A]
= (2R sin C) cos A sin A
= a cos A sin C (∵ 2R sin A = a)
Question 10.
If 4, 5 are two sides of a triangle and the included angle is 60°, find its area.
Solution:
Let a = 4, b = 5 are two sides and included angle is C = 60° then
Area of ∆ = \(\frac{1}{2}\) ab sin C
= \(\frac{1}{2}\) × 4 × 5 × sin 60°
= 2 × 5 × \(\frac{\sqrt{3}}{2}\)
= 5√3 sq.cm
![]()
Question 11.
Show that \(b \cos ^{2} \frac{C}{2}+c \cos ^{2} \frac{B}{2}=s\)
Solution:
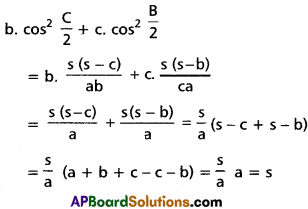
Question 12.
If \(\frac{a}{\cos A}=\frac{b}{\cos B}=\frac{c}{\cos C}\), then show that ∆ABC is equilateral.
Solution:
Given that \(\frac{a}{\cos A}=\frac{b}{\cos B}=\frac{c}{\cos C}\)
⇒ \(\frac{2 R \sin A}{\cos A}=\frac{2 R \sin B}{\cos B}=\frac{2 R \sin C}{\cos C}\)
⇒ \(\frac{\sin A}{\cos A}=\frac{\sin B}{\cos B}=\frac{\sin C}{\cos C}\)
⇒ tan A = tan B = tan C
⇒ A = B = C
⇒ ∆ABC is an equilateral triangle.
II.
Question 1.
Prove that a cos A + b cos B + c cos C = 4R sin A sin B sin C.
Solution:
L.H.S = (2R sin A) cos A + (2R sin B) cos B + (2R sin C) cos C
= R (sin 2A + sin 2B + sin 2C)
= R (2 sin (A + B) cos (A – B) + sin 2C)
= R [2 sin (180° – C) cos (A – B) + sin 2C]
= R (2 sin C . cos (A – B) + 2 sin C . cos C)
= 2R sin C (cos (A – B)) + cos C)
= 2R sin C (cos (A – B) + cos (180° – \(\overline{\mathrm{A}+\mathrm{B}}\))
= 2R sin C [cos (A – B) – cos (A + B)]
= 2R sin C (2 sin A sin B)
= 4R sin A sin B sin C
= R.H.S.
Question 2.
Prove that Σa3 sin(B – C) = 0.
Solution:
L.H.S = Σa2 [a sin (B – C)]
= Σa2 [2R . sin A sin (B – C)]
= R Σ a2 (2 sin (180° – \(\overline{\mathrm{B}+\mathrm{C}}\)) sin (B – C))
= R Σ a2 [2 sin (B + C) . sin (B – C)]
= R Σ a2 (sin2 B – sin2 C)
= R Σ a2 \(\left(\frac{b^{2}}{4 R^{2}}-\frac{c^{2}}{4 R^{2}}\right)\)
= \(\frac{1}{2 R}\) Σ[a2 (b2 – c2)]
= \(\frac{1}{2 R}\) a2 (b2 – c2) + b2 (c2 – a2) + c2 (a2 – b2)]
= \(\frac{1}{2 R}\) (a2b2 – a2c2 + b2c2 – a2b2 + a2c2 – b2c2)
= \(\frac{1}{2 R}\) × 0
= 0
= R.H.S
![]()
Question 3.
Prove that \(\frac{a \sin (B-C)}{b^{2}-c^{2}}=\frac{b \sin (C-A)}{c^{2}-a^{2}}=\frac{c \sin (A-B)}{a^{2}-b^{2}}\)
Solution:

Question 4.
Prove that \(\sum a^{2} \frac{a^{2} \sin (B-C)}{\sin B+\sin C}=0\)
Solution:

Question 5.
Prove that \(\frac{a}{b c}+\frac{\cos A}{a}=\frac{b}{c a}+\frac{\cos B}{b}=\frac{c}{a b}+\frac{\cos C}{c}\)
Solution:

Question 6.
Prove that \(\frac{1+\cos (A-B) \cos C}{1+\cos (A-C) \cos B}=\frac{a^{2}+b^{2}}{a^{2}+c^{2}}\)
Solution:

Question 7.
If C = 60°, then show that
(i) \(\frac{\mathbf{a}}{\mathbf{b}+\mathbf{c}}+\frac{\mathbf{b}}{\mathbf{c}+\mathbf{a}}=1\)
(ii) \(\frac{b}{c^{2}-a^{2}}+\frac{a}{c^{2}-b^{2}}=0\)
Solution:
∠C = 60°
⇒ c2 = a2 + b2 – 2ab cos C
⇒ c2 = a2 + b2 – 2ab cos 60°
⇒ c2 = a2 + b2 – 2ab (\(\frac{1}{2}\))
⇒ c2 = a2 + b2 – ab

Question 8.
If a : b : c = 7 : 8 : 9, find cos A : cos B : cos C.
Solution:
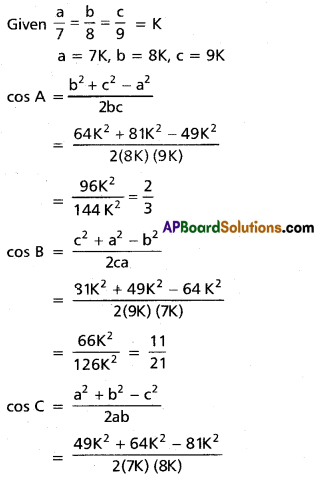

Question 9.
Show that \(\frac{\cos A}{a}+\frac{\cos B}{b}+\frac{\cos C}{c}=\frac{a^{2}+b^{2}+c^{2}}{2 a b c}\)
Solution:

Question 10.
Prove that (b – a) cos C + c (cos B – cos A) = c . sin(\(\frac{A-B}{2}\)) cosec(\(\frac{A+B}{2}\))
Solution:
L.H.S = b cos C – a cos C + c cos B – c cos A
= (b cos C + c cos B) – (a cos C + c cos A)
= a – b
= 2R (sin A – sin B)

Question 11.
Express \(a \sin ^{2} \frac{C}{2}+c \cdot \sin ^{2} \frac{A}{2}\) interms of s, a, b, c.
Solution:

Question 12.
If b + c = 3a, then rind the value of \(\cot \frac{\mathrm{B}}{2} \cot \frac{\mathrm{C}}{2}\)
Solution:

Question 13.
Prove that (b + c) cos (\(\frac{B+C}{2}\)) = a cos (\(\frac{B-C}{2}\))
Solution:

![]()
Question 14.
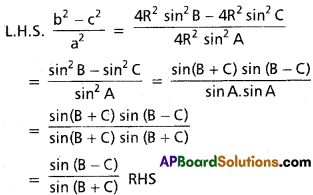
In ΔABC, show that \(\frac{b^{2}-c^{2}}{a^{2}}=\sin \frac{(B-C)}{(B+C)}\)
Solution:
III.
Question 1.
Prove that
(i) \(\cot \frac{A}{2}+\cot \frac{B}{2}+\cot \frac{C}{2}=\frac{s^{2}}{\Delta}\)
(ii) \(\tan \frac{A}{2}+\tan \frac{B}{2}+\tan \frac{C}{2}\) = \(\frac{b c+c a+a b-s^{2}}{\Delta}\)
(iii) \(\frac{\cot \frac{A}{2}+\cot \frac{B}{2}+\cot \frac{C}{2}}{\cot A+\cot B+\cot C}\) = \(\frac{(a+b+c)^{2}}{a^{2}+b^{2}+c^{2}}\)
Solution:



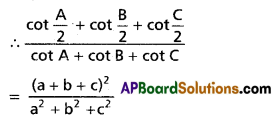
Question 2.
Show that
(i) Σ(a + b) tan(\(\frac{A-B}{2}\)) = 0
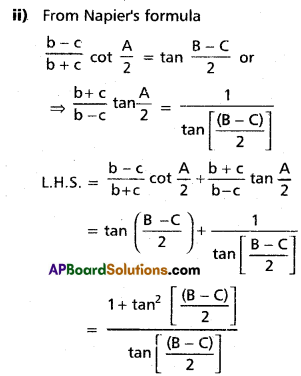
(ii) \(\frac{\mathbf{b}-\boldsymbol{c}}{\mathbf{b}+\mathbf{c}} \cot \frac{A}{2}+\frac{b+c}{b-c} \tan \frac{A}{2}\) = 2 cosec(B – C)
Solution:
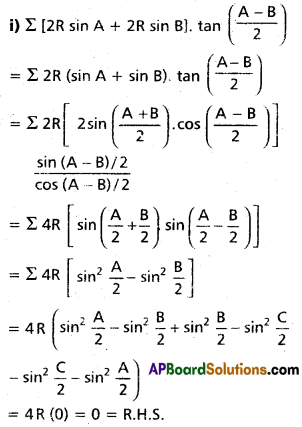
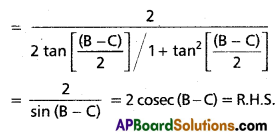
Question 3.
(i) If sin θ = \(\frac{a}{b+c}\), then show that cos θ = \(\frac{2 \sqrt{b c}}{b+c} \cdot \cos \frac{A}{2}\)
Solution:

(ii) If a = (b + c) cos θ, then prove that sin θ = \(\frac{2 \sqrt{b c}}{b+c} \cos \left(\frac{A}{2}\right)\)
Solution:

(iii) For any anlge θ show that a cos θ = b cos (C + θ) + c cos (B – θ).
Solution:
b cos (C + θ) + c cos (B – θ)
= b (cos C . cos θ – sin C sin θ) + c (cos B cos θ + sin B sin θ)
= (b cos C + c cos B) cos θ + (-b sin C + C sin B) sin θ
= a cos θ + (-2R sin B sin C + 2R sin B sin C) sin θ
= a cos θ
![]()
Question 4.
If the angles of ∆ABC are in A.P and b : c = √3 : √2 , then show that A = 75°.
Solution:
∵ The angles A, B, C of a triangle are in A.P.
⇒ 2B = A + C
⇒ 3B = A + B + C
⇒ 3B = 180°
⇒ B = 60°

Question 5.
If \(\frac{a^{2}+b^{2}}{a^{2}-b^{2}}=\frac{\sin C}{\sin (A-B)}\), prove that ∆ABC is either isosceles or right-angled.
Solution:

⇒ sin 2A = sin 2B
⇒ A = B
⇒ ∆ABC is isosceles
or 2A = 180° – 2B
or A = 90° – B
or A + B = 90°
so A ≠ B ⇒ ∆ABC is a right-angled triangle
∴ ∆ABC is either isosceles (or) right-angled.
Question 6.
If cos A + cos B + cos C = \(\frac{3}{2}\), then show that the triangle is equilateral.
Solution:

Question 7.
If cos2 A + cos2 B + cos2 C = 1, then show that ∆ABC is right-angled.
Solution:
Given cos2 A + cos2 B + cos2 C = 1 …….(1)
Now cos2 A + cos2 B + cos2 C
= cos2 A + 1 – sin2 B + cos2 C
= 1 + (cos2 A – sin2 B) + cos2 C
= 1 + cos (A + B) cos (A – B) + cos2 C
= 1 + cos (180° – C) cos (A – B) + cos2 C
= 1 – cos C . cos (A – B) + cos2 C
= 1 – cos C (cos (A – B) – cos C)
= 1 – cos C (cos (A – B) – cos (180° – \(\overline{A+B}\)))
= 1 – cos C (cos (A – B) + cos (A + B))
= 1 – cos C (2 cos A cos B)
= 1 – 2 cos A cos B cos C
Substituting in (1) we get
1 – 2 cos A cos B cos C = 1
∴ 2 cos A cos B cos C = 0
∴ cos A = 0 or cos B = 0 or cos C = 0
i.e., A = 90° or B = 90° or C = 90°
∴ ∆ABC is right-angled.
Question 8.
If a2 + b2 + c2 = 8R2, then prove that the triangle is right angled.
Solution:
Given a2 + b2 + c2 = 8R2
⇒ 4R2 (sin2 A + sin2 B + sin2 C) = 8R2
⇒ sin2 A + sin2 B + sin2 C = 2 ……(1)
Now sin2 A + sin2 B + sin2 C
= 1 – cos2 A + sin2 B + sin2 C
= 1 – (cos2 A – sin2 B) + sin2 C
= 1 – cos (A + B) . cos (A – B) + sin2 C
= 1 – cos (180° – C) cos (A – B) + sin2 C
= 1 + cos C cos (A – B) + 1 – cos2 C
= 2 + cos C (cos (A – B) – cos C)
= 2 + cos C (cos (A – B) – cos (180° – \(\overline{A+B}\)))
= 2 + cos C (cos (A – B) + cos (A + B))
= 2 + cos C (2 cos A cos B)
= 2 + 2 cos A cos B cos C
Substituting in (1), we get
2 + 2 cos A cos B cos C = 2
2 cos A cos B cos C = 0
⇒ cos A = 0 or cos B = 0 or cos C = 0
∴ A = 90° or B = 90° or C = 90°
∴ ΔABC is right-angled.
![]()
Question 9.
If cot \(\frac{A}{2}\), cot \(\frac{B}{2}\), cot \(\frac{C}{2}\) are in A.P., then prove that a, b, c are in A.P.
Solution:
∵ cot \(\frac{A}{2}\), cot \(\frac{B}{2}\), cot \(\frac{C}{2}\) are in A.P
⇒ \(\frac{(s)(s-a)}{\Delta}, \frac{(s)(s-b)}{\Delta}, \frac{(s)(s-c)}{\Delta}\) are in A.P.
⇒ s – a, s – b, s – c are in A.P
⇒ -a, -b, -c are in A.P
⇒ a, b, c are in A.P
Question 10.
If \(\sin ^{2} \frac{A}{2}, \sin ^{2} \frac{B}{2}, \sin ^{2} \frac{C}{2}\) are in H.P., show that a, b, c are in H.P.
Solution:
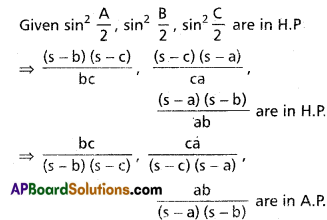

Question 11.
If C = 90° then prove that \(\frac{a^{2}+b^{2}}{a^{2}-b^{2}}\) sin (A – B) = 1
Solution:

Question 12.
Show that \(\frac{a^{2}}{4} \sin 2 C+\frac{c^{2}}{4} \sin 2 A\) = ∆
Solution:
LHS = \(\frac{a^{2}}{4} \sin 2 C+\frac{c^{2}}{4} \sin 2 A\)
= \(\frac{4 R^{2} \sin ^{2} A}{4}\) 2 sin C cos C + \(\frac{4 R^{2} \sin ^{2} C}{4}\) 2 sin A cos A
= 2R2 sin2A sin C cos C + 2R2 sin2C sin A cos A
= 2R2 sin A sin C (sin A cos C + cos A sin C)
= 2R2 sin A sin C sin(A + C)
= 2R2 sin A sin C sin(180 – B)
= 2R2 sin A sin B sin C
= ∆
= RHS
Question 13.
A lamp post is situated at the middle point I the side AC of a triangular plot A with BC = 7 meters, CA = 8 meters, and AB = 9 meters, lamp post subtends an angle of 15° at point B. find H height of the lamp post.
Solution:
Let MP be the height of the lamp post
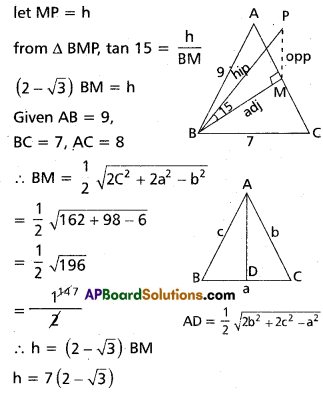
Question 14.
Two ships leave a port at the same time. One goes 24 km. per hour in the direction N45°E and other travels 32 km per hour in the direction S75°E. Find the distance between the ships at the end of 3 hours.
Solution:
Given the first ship goes 24 km per hour After 3 hours the first ship goes 72 km.
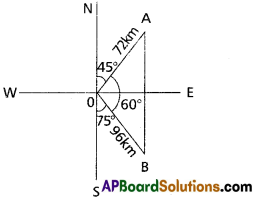
Given the second ship goes 32 km per hour After 3 hours, the second ship goes 96 km.
Let AB = x
∠AOB = 180° – (75 + 45) = 60°
Apply cosine rule for ∆AOB,
cos 60° = \(\frac{(72)^{2}+(96)^{2}-x^{2}}{2(72)(96)}\)
⇒ \(\frac{1}{2}=\frac{5184+9216-x^{2}}{13824}\)
⇒ 13824 = 28800 – 2x2
⇒ 2x2 = 14976
⇒ x2 = 7488
⇒ x = 86.4 (Appx)
At the end of 3 hours the difference between ships was 86.4 km.
![]()
Question 15.
A tree stands vertically on the slant of the hill. From A point on the ground 35 meters down the hill from the base of the tree, the angle, the elevation of the top of the tree is 60° if the angle of elevation of the foot of the tree from A is 15°, then find the height of the tree.
Solution:
Let BC be the height of the tree
BC = h
Let BD = x, AD = y
Given AB = 35 m

Question 16.
The upper \(\frac{3}{4}\)th portion of a vertical pole subtends an angle tan-1(\(\frac{3}{5}\)) at a point in the horizontal plane through its foot and at a distance 40 m from the foot. Given that the vertical pole is at a height less than 100 m from the ground, find its height.
Solution:

⇒ 6400 + h2 = 200h
⇒ h2 – 200h + 6400 = 0
⇒ h2 – 160h – 40h + 6400 = 0
⇒ h(h – 160) – 40(h – 160) = 0
⇒ (h – 160) (h – 40) = 0
⇒ h = 40 or 160
but the height of the pole should be less than 100m
∴ h = 40 m
Question 17.
AB is a vertical pole with B at the ground level and A at the top. A man finds that the angle of elevation of point A from a certain point C on the ground is 60°. He moves away from the pole along the line BC to a point D such that CD = 7 m. From D, the angle of elevation of point A is 45°. Find the height of the pole.
Solution:
Let ‘h’ be the height of the pole
AB = h
given CD = 7 m
∠ACB = 60°, ∠ADB = 45°, Let BC = x

![]()
Question 18.
Let an object be placed at some height h cm and let P and Q two points of observation which are at a distance of 10 cm apart on a line inclined at an angle of 15° to the horizontal. If the angles of elevation of the object from P and Q are 30° and 60° respectively then find h.
Solution:
Let AB = Height of the object from ‘A’ = h m
Given that P & Q are two observations,
PQ = 10 cms
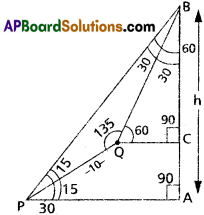
From ∆APB,
∠P = 30; ∠A = 90; ∠B = ?
A + P + B = 180°
⇒ 30° + 30° + B = 180°
⇒ B = 180° – 120°
⇒ B = 60°
From ∆BQC,
∠Q = 60°; ∠C = 90°; ∠B = ?
Q + C + B = 180°
⇒ 60° + 90° + B = 180°
⇒ B = 180° – 150°
⇒ B = 30°
From ∆BQP,
∠P = 15; ∠B = 30; ∠Q = ?
P + B + Q = 180°
⇒ 15° + 30° + Q = 180°
⇒ Q = 180° – 45°
⇒ Q = 135°
Applying the ‘sin’ rule for ∆BQP

From ∆PAB,
sin 30° = \(\frac{B A}{B P}\)
BP . sin 30° = AB = h
√2 × 10 × \(\frac{1}{2}\) = AB = h
5√2 = AB = h
∴ h = 5√2