Inter 1st Year Maths 1A Hyperbolic Functions Solutions Ex 9(a)

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Hyperbolic Functions Solutions Exercise 9(a) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Hyperbolic Functions Solutions Exercise 9(a)

Question 1.
If sinh x = \(\frac{3}{4}\), find cosh (2x) and sinh (2x).
Solution:

Question 2.
If sinh x = 3, then show that x = log_e(3 + √10).
Solution:

Question 3.
Prove that
(i) tanh (x – y) = \(\frac{\tanh x-\tanh y}{1-\tanh x \tanh y}\)
Solution:

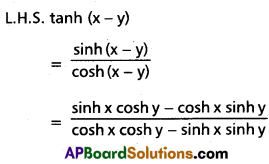
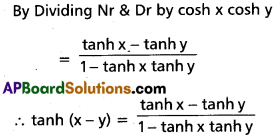
(ii) coth (x – y) = \(\frac{{coth} x \cdot {coth} y-1}{{coth} y-{coth} x}\)
Solution:

Question 4.
Prove that
(i) (cosh x – sinh x)ⁿ = cosh (nx) – sinh (nx), for any n ∈ R.
Solution:

(ii) (cosh x + sinh x)ⁿ = cosh (nx) + sinh (nx), for any n ∈ R.
Solution:

Question 5.
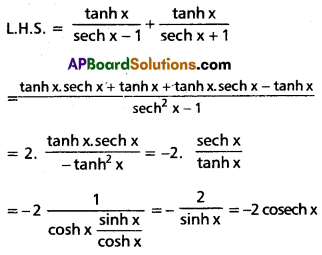
Prove that \(\frac{\tanh x}{{sech} x-1}+\frac{\tanh x}{{sech} x+1}\) = -2 cosech x, for x ≠ 0
Solution:

Question 6.
Prove that \(\frac{\cosh x}{1-\tanh x}+\frac{\sinh x}{1-{coth} x}\) = sinh x + cosh x, for x ≠ 0
Solution:

Question 7.
For any x ∈ R, prove that cosh⁴x – sinh⁴x = cosh (2x)
Solution:
L.H.S = cosh⁴x – sinh⁴x
= (cosh²x)² – (sinh²x)²
= [cosh²x – sinh²x] [cosh²x + sinh²x]
= (1) cosh (2x)
= cosh (2x)
∴ cosh⁴x – sinh⁴x = cosh (2x)

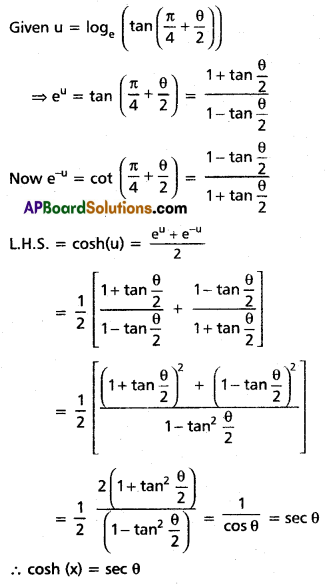
Question 8.
If u = \(\log _{e}\left(\tan \left(\frac{\pi}{4}+\frac{\theta}{2}\right)\right)\) and if cos θ > 0,then prove that cosh u = sec θ.
Solution: