Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Applications of Derivatives Solutions Exercise 10(f) will help students to clear their doubts quickly.
Intermediate 1st Year Maths 1B Applications of Derivatives Solutions Exercise 10(f)
I.
Question 1.
Verify Rolle’s theorem for the following functions.
i) x² – 1 on [-1, 1]
Solution:
Let f(x) = x² – 1
f is continuous on [-1,1]
since f(-1) = f(1) = 0 and
f is differentiable on [-1, 1]
∴ By Rolle’s theorem ∃ c ∈ (-1, 1) such that f'(c) = 0
f'(x) = 2x = 0
∴ = f'(c) = 0
2c = 0
c = 0
The point c = 0 ∈ (-1, 1)
Then Rolle’s theorem is verified.
ii) sin x – sin 2x on [0, π].
Solution:
Let f(x) = sin x – sin 2x
f is continuous on [0, π]
since f(0) = f(π)= 0 and
f is differentiable on [0, π]
By Rolle’s theorem ∃ c ∈ (0, π)
such that f'(c) = 0
f'(x) = cos x – 2 cos 2x
f'(c) = 0 ⇒ cosc – 2 cos 2c = 0
⇒ cosc – 2(2cos²c – 1):
cosc – 4 cos²c + 2=0 2
4 cos² c – cosc – 2 = 0
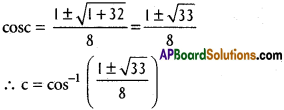
iii) log (x² + 2) – log 3 on [-1, 1]
Solution:
Let f(x) = log (x² + 2) – log 3
f is continuous on [-1, 1]
Since f(-1) = f(1) = 0 and f is
Differentable on [-1, 1]
By Rolle’s theorem ∃ c ∈ (-1, 1)
Such that f'(c) = 0
f'(x) = \(\frac{1}{x^{2}+2}\) = (2x)
f'(x) = \(\frac{2c}{c^{2}+2}\) = 0
2c = 0
c = 0
c = 0 ∈ (-1, 1).
![]()
Question 2.
It is given that Rolle’s theorem holds for the function f(x) = x³ + bx² + ax on [1, 3] with c = 2t + \(\frac{1}{\sqrt{3}}\). Find the values of a and b.
Solution:
Given f(x) = x³ + bx² + ax
f'(x) = 3x² + 2bx + a
∴ f'(c) = 0 6 ⇔ 3c² + 2bc + a = 0

⇔ b = 6 and b² – 3a = 3
36 – 3 = 3a
33 = 3a
a = 11
Hence a = 11 and b = -6.
Question 3.
Show that there is no real number k, for which the equation x² – 3x + k = 0 has two distinct roots in [0, 1].
Solution:
Clearly f(0) = f(c)
0 – 0 + k = 1 – 3 + k
0 = -2
Which is not possible
∴ There is no real number K.
Question 4.
Find a point on the graph of the curve y = (x – 3)², where the tangent is parallel to the chord joining (3, 0) and (4, 1).
Solution:
Given points (3, 0) and (4, 1)
The slope of chord = \(\frac{1-0}{4-3}\) = 1
Given y = (x- 3)²
\(\frac{dy}{dx}\) = 2(x – 3)
⇒ Slope = 2(x – 3)
1 = 2(x – 3)
\(\frac{1}{2}\) = x – 3
x = \(\frac{1}{2}\) + 3 = \(\frac{7}{2}\)
y = (x – 3)² = (\(\frac{7}{2}\) – 3)² = \(\frac{1}{4}\)
∴ The point on the curve is (\(\frac{7}{2}\), \(\frac{1}{4}\))
Question 5.
Find a point on the graph of the curve y = x³, where the tangent is parallel to the chord joining (1, 1) and (3, 27).
Solution:
Given points (1, 1) and (3, 27)
Slope of chord = \(\frac{27-1}{3-1}\) = 13
Given y = x³
\(\frac{dy}{dx}\) = 3x²
⇒ Slope = 3x²
13 = 3x²
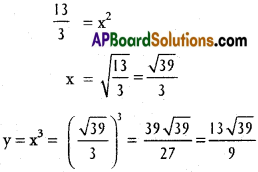
∴ The point on the curve is (\(\frac{\sqrt{39}}{3}\), \(\frac{13\sqrt{39}}{9}\))
![]()
Question 6.
Find ‘c’, so that f'(c) = \(\frac{f(b)-f(a)}{b-a}\) in the following cases.
i) f(x) = x² – 3x – 1, a = \(\frac{-11}{7}\), b = \(\frac{13}{7}\).
Solution:
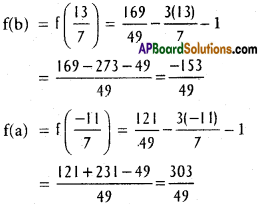
f'(x) = 2x – 3
f'(c) = 2c – 3
Given f'(c)= \(\frac{f(b)-f(a)}{b-a}\)

ii) f(x) = ex ; a = 0, b = 1
Solution:
f(b) = f(1) = e’ = e
f(a) = f(0) = e° = 1
Given f(x) = ex
f'(x) = ex
Given condition f'(c) = \(\frac{f(b)-f(a)}{b-a}\)

Question 7.
Verify the Rolle’s theorem for the function (x² – 1) (x – 2) on [-1, 2]. Find the point in the interval where the derivate vanishes.
Solution:
Let f(x) = (x² – 1) (x- 2) = x³ – 2x² – x + 2
f is continous on [-1, 2]
since f(-1) = f(2) = 0 and f is
Differentiable on [-1, 2]
By Rolle’s theorem ∃ C ∈ (-1, 2)
Let f'(c) = 0
f'(x) = 3x² – 4x – 1
3c² – 4c – 1 = 0
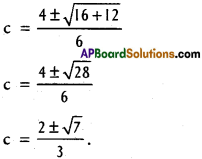
Question 8.
Verify the conditions of the Lagrange’s mean value theorem for the following functions. In each case find a point ‘c’ in the interval as stated by the theorem
i) x² -1 on [2, 3]
Solution:
Solution:
Let f(x) = x² – 1
f is continous on [2, 3]
and f is differentiable
Given f(x) = x² – 1
f'(x) = 2x
By Lagrange’s mean value theorem ∃ C ∈ (2, 3) such there
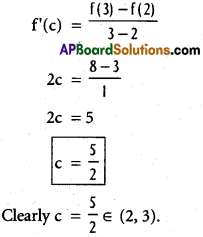
ii) sin x – sin 2x on [0, π]
Solution:
Let f(x) = sin x – sin 2x
f is continuous on [0, π] and f is differentiable
Given f(x) = sin x – sin 2x
f'(x) = cos x – 2 cos 2x
By Lagrange’s mean value than ∃ C ∈ (0, π) such there
f'(c) = \(\frac{f(\pi)-f(0)}{\pi-0}\)
cosc – 2 cos 2c = 0
cosc 2(2cos² – 1) = 0
cosc – 4 cos²c + 2 = 0
4 cos² c – cos c – 2 = 0
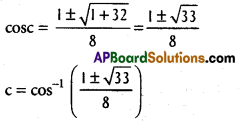
![]()
iii) log x on [1, 2].
Solution:
Let f(x) = log x
f is continuous on [1, 2] and f is differentiable
Given f(x) = log x
f'(x) = \(\frac{1}{x}\)
By Lagrange’s mean value theorem ∃ c ∈ (1, 2) such that
