Inter 1st Year Maths 1B Differentiation Solutions Ex 9(b)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Differentiation Solutions Exercise 9(b) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B Differentiation Solutions Exercise 9(b)

I. Compute the following limits.

Question 1.
Find the derivatives of the following function.
i) cotⁿ x
Solution:
\(\frac{dy}{dx}\) = n. cot^n-1 x. \(\frac{d}{dx}\) (cot x)
= n. cot^n-1 x (- cosec² x)
= – n. cot^n-1 x. cosec² x

ii) cosec⁴ x
Solution:
\(\frac{dy}{dx}\) = 4.cosec³ x. \(\frac{d}{dx}\)(cosec x)
= 4. cosec³ x (- cosec x. cot x)
= – 4. cosec⁴ x. cot x

iii) tan (e^x)
=sec 2(e^x).(e^x)¹
= e^x. sec² (e^x)

iv) \(\frac{1-\cos 2 x}{1+\cos 2 x}\)
Solution:
\(\frac{2 \sin ^{2} x}{2 \cos ^{2} x}\) = tan² x \(\frac{dy}{dx}\) = 2 tan x . sec² x

v) sin^m x cosⁿ x
Solution:
\(\frac{dy}{dx}\) = (sin^m x). \(\frac{d}{dx}\) (cosⁿ x) + (cosⁿ x) \(\frac{d}{dx}\) (sin^m x)
= sin^m xn + cos^n-1 x(-sin x) + cosⁿ x. m sin^m-1 x. cos x
= m. cosⁿ⁺¹ x. sin^m-1 x – n. sin^m+1 x. cos^n-1 x.

vi) sin mx. cos nx
Solution:
\(\frac{dy}{dx}\) = sin mx \(\frac{d}{dx}\) (cos nx) + (cos nx) \(\frac{dy}{dx}\) (sin mx)
= sin mx (-n sin nx)+cos nx (m cos mx)
= m. cos mx. cos nx – n. sin mx . sin nx

vii) x tan^-1 x
Solution:
\(\frac{dy}{dx}\) = x. \(\frac{d}{dx}\) (tan^-1 x) + (tan^-1 x) \(\frac{d}{dx}\) (x)
= \(\frac{x}{1+x^{2}}\) + tan^-1 x.

viii) sin^-1 (cos x)
Solution:
= sin^-1 [sin (\(\frac{\pi}{2}\) – x)] = \(\frac{\pi}{2}\) – x
\(\frac{dy}{dx}\) = 0 – 1 = -1

ix) log (tan 5x)
Solution:

x) sinh^-1 (\(\frac{3x}{4}\))
Solution:

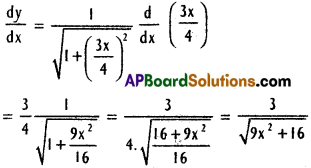
xi) tan^-1 (log x)
Solution:

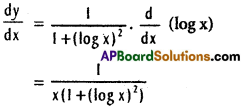
xii) log (\(\frac{x^{2}+x+2}{x^{2}-x+2}\))
Solution:
\(\frac{dy}{dx}\) = log(x² + x + 2) – log(x² – x + 2)

xiii) log (sin^-1 (e^x))
Solution:

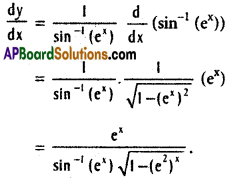
xiv) (sin x)² (sin^-1 x)²
Solution:

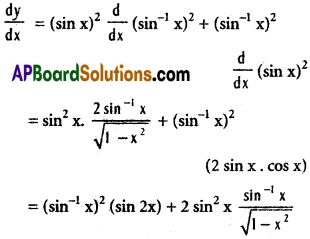
xv) y = \(\frac{\cos x}{\sin x+\cos x}\)
Solution:

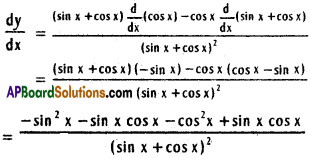
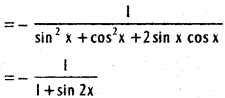
xvi) \(\frac{x\left(1+x^{2}\right)}{\sqrt{1-x^{2}}}\)
Solution:

xvii) y = e^sin-1x
Solution:

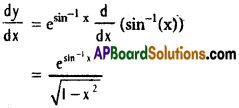
xviii) y = cos (log x + e^x)
Solution:
\(\frac{dy}{dx}\) = -sin(log x + e^x) = \(\frac{d}{dx}\) (log x + e^x)
= -sin (log x + e^x) (\(\frac{1}{x}\) + e^x)

xix) y = \(\frac{\sin (x+a)}{\cos x}\)
Solution:

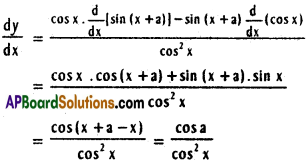
xx) y = cot^-1 (coses 3x)
Solution:

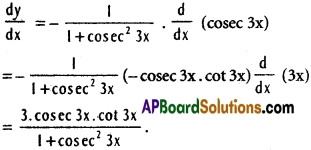
Question 2.
Find the derivatives of the following fountion.
i) x = sinh² y
Solution:
\(\frac{dy}{dx}\) = 2 sinh y . cosh y

ii) x = tanh² y
Solution:
\(\frac{dy}{dx}\) = 2 tanh y . sech² y

iii) x = e^{sinh y}
Solution:
\(\frac{dy}{dx}\) = e^{sinh y} \(\frac{d}{dx}\) (sinh y)
= e^{sinh y} . cosh y
= x. cosh y
\(\frac{d y}{d x}=\frac{1}{\left(\frac{d x}{d y}\right)}=\frac{1}{x \cdot \cosh y}\)

iv) x =tan (e^-y)
Solution:
\(\frac{dy}{dx}\) = sec² (e^-y) . (e^-y)¹ = -e^-y . sec² e^-y
= -e^-y(1 + tan² (e^-y) = – e^-y(1 + x²)
\(\frac{d y}{d x}=\frac{1}{\left(\frac{d x}{d y}\right)}=-\frac{1}{e^{-y}\left(1+x^{2}\right)}=-\frac{e^{y}}{1+x^{2}}\)

v) x = log (1 + sin² y)
Solution:

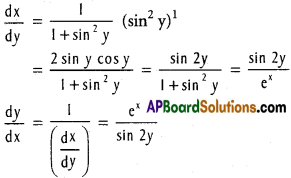
vi) x = log (1 + √y)
Solution:
1 + √y = e^x
√y = e^x – 1
y = (e^x – 1)²
\(\frac{dy}{dx}\) = 2(e^x – 1) . e^x = 2 √y . e^x
= 2 √y (√y + 1)
= 2(y + √y)

II. Find the derivativies of the following functions.

i) y = cos [log (cot x)]
Solution:

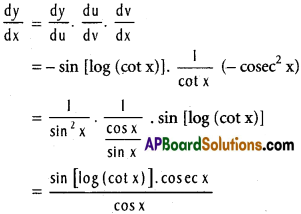
ii) y = sin^-1 \(\frac{1-x}{1+x}\)
Solution:

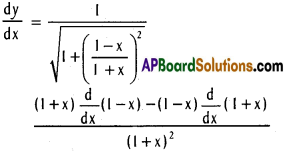
iii) log (cot (1 – x²))
Solution:

iv) y = sin [cos (x²)]
Solution:
\(\frac{dy}{dx}\) = cos [cos (x²)].\(\frac{d}{dx}\)[cos (x²)]
= cos [cos (x²)](sin (x²)).\(\frac{d}{dx}\)(x²)
= – 2x. sin (x²). cos [cos (x²)]

v) y = sin [tan^-1 (e^x)]
Solution:

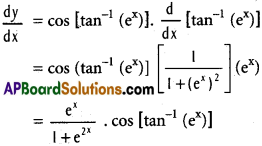
vi) y = \(\frac{\sin (a x+b)}{\cos (c x+d)}\)
Solution:

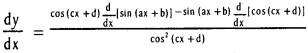
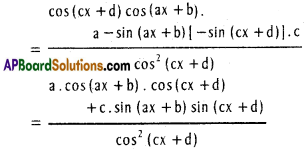
vii) y = tan^-1 (tan h \(\frac{x}{2}\))
Solution:

viii) y = sinx . (Tan^-1x)²
Solution:

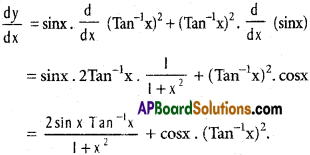
III. Find the derivatives of the following functions.

Question 1.
y = sin^-1 \(\left(\frac{b+a \sin x}{a+b \sin x}\right)\) (a > 0, b > 0)
Solution:
Let u = \(\frac{b+a \sin x}{a+b \sin x}\)

Question 2.
cos^-1\(\left(\frac{b+a \cos x}{a+b \cos x}\right)\) (a > 0, b > 0)
Solution:
Let u = \(\frac{b+a \cos x}{a+b \cos x}\)

Question 3.
tan^-1 \(\left[\frac{\cos x}{1+\cos x}\right]\)
Solution:
Let u = \(\frac{\cos x}{1+\cos x}\)