Inter 1st Year Maths 1B Direction Cosines and Direction Ratios Formulas

Use these Inter 1st Year Maths 1B Formulas PDF Chapter 6 Direction Cosines and Direction Ratios to solve questions creatively.

Intermediate 1st Year Maths 1B Direction Cosines and Direction Ratios Formulas

Formulae and Synopsis :
If a line PQ makes angles α, β, γ with the co – ordinate axes, then cos α, cos β, cos γ are called
direction cosines of the line PQ. We take
l = cos α, m = cos β and n = cos γ
Relation between direction cosines is l² + m² + n² = 1

Direction Ratios :
An ordered triple of numbers proportional to the direction cosines of a line are defined as ‘Direction ratios’ of that fine.

→ If \(\frac{1}{a}=\frac{m}{b}=\frac{n}{c}\) then a, b, c are called direction ratios of the line.

→ If a, b, c are the direction ratios of a line, then its direction cosines are \(\left(\frac{a}{\sqrt{a^{2}+b^{2}+c^{2}}}, \frac{b}{\sqrt{a^{2}+b^{2}+c^{2}}}, \frac{c}{\sqrt{a^{2}+b^{2}+c^{2}}}\right)\)

→ Direction ratios of the line joining P(x₁, y₁, z₁) and Q (x₂, y₂, z₂) are (x₂ – x₁, y₂ – y₁, z₂ – z₁) or (x₁ – x₂, y₁ – y₂, z₁ – z₂)

→ D.cs of the above line \(\frac{x_{2}-x_{1}}{P Q}, \frac{y_{2}-y_{1}}{P Q}, \frac{z_{2}-z_{1}}{P Q}\) or \(\frac{x_{1}-x_{2}}{P Q}, \frac{y_{1}-y_{2}}{P Q}, \frac{z_{1}-z_{2}}{P Q}\)

→ Angle between the lines whose D.cs are (l₁ m₁, n₁) and (l₂, m₂, n₂) is given by cos θ = l₁l₂ + m₁m₂ + n₁n₂

→ If these lines are perpendicular, then l₁l₂ + m₁m₂ + n₁n₂ = 0

Angle Between Two Lines:
The angle between two skew lines is the angle between two lines drawn parallel to them through any point in space.

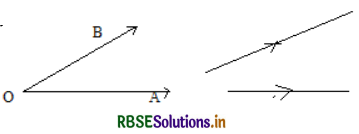
Direction Cosines:
If α, β, γ are the angles made by a directed line segment with the positive directions of the coordinate axes respectively, then cos α, cos β, cos γ are called the direction cosines of the given line and they are denoted by l, m, n respectively Thus l = cos α, m = cos β, n = cos γ

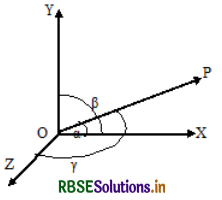
The direction cosines of \(\overline{o p}\) are l = cos α, m = cos β, n = cos γ.
If l, m, n are the d.c’s of a line L is one direction then the d.c’s of the same line in the opposite direction are -l, -m, -n.

Note :

• The angles α, β, γ are known as the direction angles and satisfy the condition 0 < α, β, γ < π.
• The sum of the angles α, β, γ is not equal to 2β because they do not lie in the same plane.
• Direction cosines of coordinate axes.

The direction cosines of the x-axis are cos0, cos\(\frac{\pi}{2}\), cos\(\frac{\pi}{2}\) i.e., 1, 0, 0
Similarly the direction cosines of the y-axis are (0, 1, 0) and z-axis are (0, 0, 1)

Theorem:
If P(x, y, z) is any point in space such that OP = r and if l, m, n are direction cosines of \(\overline{O P}\) then x = lr,y = mr, z = nr.
Note: If P(x, y, z) is any point in space such that OP = r then the direction cosines of \(\overline{O P}\) are
Note: If P is any point in space such that OP =r and direction cosines of OP are l,m,n then the point P =(lr,mr,nr)
Note: If P(x,y,z) is any point in space then the direction cosines of OP are \(\frac{x}{\sqrt{x^{2+} y^{2}+z^{2}}}, \frac{y}{\sqrt{x^{2+} y^{2}+z^{2}}}, \frac{z}{\sqrt{x^{2+} y^{2}+z^{2}}}\)

Theorem:
If l, m, n are the direction cosines of a line L then l² + m² + n² = 1.
Proof:

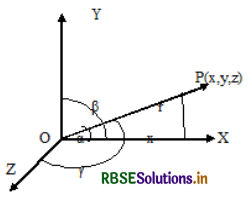
l = cos α = \(\frac{x}{r}\), m = cos β = \(\frac{y}{r}\), n = cos γ = \(\frac{z}{r}\) ⇒ cos²α + cos²β + cos²γ = \(\frac{x^{2}}{r^{2}}+\frac{y^{2}}{r^{2}}+\frac{z^{2}}{r^{2}}\)
= \(\frac{x^{2}+y^{2}+z^{2}}{r^{2}}=\frac{r^{2}}{r^{2}}\)
∴ l² + m² + n² = 1

Theorem:
The direction cosines of the line joining the points P(x₁, y₁, z₁),Q(x₂, y₂, z₂) are
\(\left(\frac{x_{2}-x_{1}}{r}, \frac{y_{2}-y_{1}}{r}, \frac{z_{2}-z_{1}}{r}\right)\) where r = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}+\left(z_{2}-z_{1}\right)^{2}}\)

Direction Ratios:
A set of three numbers a,b,c which are proportional to the direction cosines l,m,n respectively are called DIRECTION RATIOS (d.r’s) of a line.
Note : If (a, b, c) are the direction ratios of a line then for any non-zero real number λ , (λa, λb, λc) are also the direction ratios of the same line.
Direction cosines of a line in terms of its direction ratios
If (a, b, c) are direction ratios of a line then the direction cosines of the line are ±\(\left(\frac{a}{\sqrt{a^{2}+b^{2}+c^{2}}}, \frac{b}{\sqrt{a^{2}+b^{2}+c^{2}}}, \frac{c}{\sqrt{a^{2}+b^{2}+c^{2}}}\right)\)

Theorem:
The direction ratios of the line joining the points are (x₂ – x₁, y₂ – y₁, z₂ – z₁)

Angle Between Two Lines:
If (l₁, m₁, n₁) and (l₂, m₂, n₂) are the direction cosines of two lines θ and is the acute angle between them, then cos θ = |l₁l₂ + m₁m₂ + n₁n₂|

Note.
If θ is the angle between two lines having d.c’s (l₁, m₁, n₁) and (l₂, m₂, n₂) then
sin θ = \(\sqrt{\sum\left(l_{1} m_{2}-l_{2} m_{1}\right)^{2}}\) and tan θ = \(\frac{\sqrt{\sum\left(l_{1} m_{2}-l_{2} m_{1}\right)^{2}}}{\left|l_{1} l_{2}+m_{1} m_{2}+n_{1} n_{2}\right|}\) where θ ≠ \(\frac{\pi}{2}\)

Note :
The condition for the lines to be perpendicular is l₁l₂ + m₁m₂ + n₁n₂ = 0
The condition for the lines to be parallel is \(\frac{l_{1}}{l_{2}}=\frac{m_{1}}{m_{2}}=\frac{n_{1}}{n_{2}}\)

Theorem:
If (a₁, b₁, c₁) and (a₂, b₂, c₂) are direction ratios of two lines and θ is the angle
between them then cos θ = \(\frac{a_{1} a_{2}+b_{1} b_{2}+c_{1} c_{2}}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}} \sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}\)

Note:

• If the two lines are perpendicular then a₁a₂ + b₁b₂ + c₁c₂ = 0
• If the two lines are parallel then \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
• If one of the angle between the two lines is 0 then other angle is 180° – θ