Use these Inter 1st Year Maths 1B Formulas PDF Chapter 7 The Plane to solve questions creatively.
Intermediate 1st Year Maths 1B The Plane Formulas
Definition: If F(x, y, z) is a polynomial of degree one, then the surface represented by F(x, y, z).= 0 is called a first degree
→ If A, B, C are three non-collinear points in space, then there exists exactly only one plane through A,
→ If a plane contains two points A and B, then the plane also contains the line \(\overleftrightarrow{A B}\).
→ If two planes intersect, then their intersection is a line.
→ If a plane π and a line L are perpendicular at a point P, then π contains every line that passes through P and is perpendicular to L.
→ Equation of a plane in the normal form is lx + my + nz = p. Hence (l, m, n) are D.C’s of the normal to the plane, and p( > 0) is the perpendicular distance of the plane from the origin.
→ If (a, b, c) & (0,0,0), then the equation ax + by + cz + d = 0 is called the general form of the equation of a plane.
→ Equation of the plane n which contains the point A(x0, y0, z0) and perpendicular to the line L with direction ratios (a, b, c) is a(x – xQ) + b(y – y0) + c(z – z ) = 0.
![]()
→ Equation of the plane passing through three non-collinear point A(x1, y1; z1), B(x2, y2, z2) and C(x3 y3, z3) is \(\left|\begin{array}{ccc}
x-x_{1} & y-y_{1} & z-z_{1} \\
x_{2}-x_{1} & y_{2}-y_{1} & z_{2}-z_{1} \\
x_{3}-x_{1} & y_{3}-y_{1} & z_{3}-z_{i}
\end{array}\right|\) = 0
→ Equation of the plane in the intercept form is \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 1.
→ The angle between the planes a1x + b1y + c1z + d1 = 0 and a2x + b2y + c2z + d2 = 0 is cos-1 \(\frac{\left|a_{1} a_{2}+b_{1} b_{2}+c_{1} c_{2}\right|}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}} \sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}\)
→ The perpendicular distance of the plance ax + by + cz + d = 0 from the point P(x0 , y0 , z0) is \(\frac{\left|a x_{0}+b y_{0}+c z_{0}+d\right|}{\sqrt{a^{2}+b^{2}+c^{2}}}\)
→ The distance between the parallel planes ax + by + cz + d1 = 0 and ax + by + cz + d2 = 0 is \(\frac{\left|d_{1} \cdot d_{2}\right|}{\sqrt{a^{2}+b^{2}+c^{2}}}\)
Planes:
Definition:
A surface in space is said to be a plane surface or a plane if all the points of the straight line joining any two points of the surface lie on the surface.
Theorem:
The equation of the plane passing through a point (x1, y1, z1) and perpendicular to a line whose direction ratios are a, b, c is a( x – x1)+b( y – y1)+c( z – z1) = 0
Theorem:
The equation of the plane passing through a point (x1, y1, z1) is a( x – x1)+b( y – y1)+c (z – z1) = 0 where a,b,c are constants.
Theorem:
The equation of the plane containing three points (x1, y1, z1), (x2, y2, z2), (x3, y3, z3) is \(\left|\begin{array}{ccc}
x-x_{1} & y-y_{1} & z-z_{1} \\
x_{2}-x_{1} & y_{2}-y_{1} & z_{2}-z_{1} \\
x_{3}-x_{1} & y_{3}-y_{1} & z_{3}-z_{1}
\end{array}\right|\) = 0
Normal Form of A Plane:
Theorem:
The equation of the plane which is at a distance of p from the origin and whose normal has the direction cosines (l, m, n) is lx + my + nz = p (or) x cos α+ y cos β + z cos γ = p.
Note:
Equation of the plane through the origin is lx + my + nz = 0
Note: The equation of the plane ax +by+cz+d=0 in the normal form is
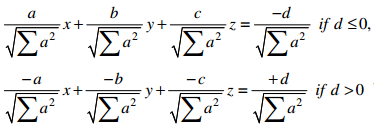
where Σa2 = a2 + b2 + c2
![]()
Perpendicular Distance From A Point to A Plane:
The perpendicular distance from the origin to the plane ax + by + cz + d = 0 is \(\frac{|d|}{\sqrt{a^{2}+b^{2}+c^{2}}}\)
Theorem
The perpendicular distance from P(x1, y1, z1) to the plane ax + by + cz + d = 0 is \(\frac{\left|a x_{1}+b y_{1}+c z_{1}+d\right|}{\sqrt{a^{2}+b^{2}+c^{2}}}\)
Theorem
Intercept form of the plane
The equation of the plane having a,b,c as x, y, z- intercepts respectively is \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 1
Theorem
The intercepts of the plane ax + by + cz + d = 0 are respectively \(\frac{-d}{a}, \frac{-d}{b}, \frac{-d}{c}\)
Angle Between Two Planes:
Definition: The angle between the normals to two planes is called the angle between the planes.
Theorem:
If θ is the angle between the planes a1x + b1 y + c1z + d1 = 0, a2x + b2y + c2z + d2 = 0 then cos θ = \(\frac{a_{1} a_{2}+b_{1} b_{1}+c_{1} c_{2}}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}} \sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}\)
Note:
- If θ is acute then cos θ = \(\frac{a_{1} a_{2}+b_{1} b_{1}+c_{1} c_{2}}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}} \sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}} \mid\)
- The planes a1x + b1 y + c1z + d1 = 0, a2x + b2y + c2z + d2 = 0 are
- parallel iff \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
- Perpendicular iff . a1a2 + b1b2 + c1c2 = 0
- The given planes are perpendicular
⇔ θ = 90° ⇔ cos θ = 0 ⇒ a1a2 + b1b2 + c1c2 = 0
Theorem:
The equation of the plane parallel to the plane ax + by + cz + d = 0 is ax + by + cz + k = 0 where k is a constant.
Theorem:
The distance between the parallel planes ax + by + cz + d1 = 0, ax + by + cz + d2 = 0 is \(\frac{\left|d_{1}-d_{2}\right|}{\sqrt{a^{2}+b^{2}+c^{2}}}\)