Students get through Maths 1B Important Questions Inter 1st Year Maths 1B The Plane Important Questions which are most likely to be asked in the exam.
Intermediate 1st Year Maths 1B The Plane Important Questions
Question 1.
Find the equation of the plane if the foot of the perpendicular from origin to the plane is (2, 3, -5).
Solution:
O (0, 0, 0), P (2, 3, -5) are the given points D.Rs of OP are 2, 3, -5
OP is normal to the plane and it passes through p (2, 3,-5)
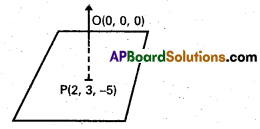
Equation of the plane is
2(x – 2) + 3(y – 3) – 5(z + 5)
2x – 4 + 3y – 9 – 5z – 25 = 0
2x + 3y – 5z – 38 = 0
Question 2.
Find the equation to the plane through the points (0, -1, -1) (4, 5, 1) and (3, 9, 4).
Solution:
A (0, -1, -1), B (4, 5, 1), C (3, 9, 4) are the given points.
Equation of the plane through A can be take as
a (x – 0) + b(y + 1) + c (z + 1) = 0 ………………… (1)
The plane passes through B (4, 5, 1), C (3, 9, 4)
4a + 6b + 2c = 0 ………………. (2)
3a + 10b + 5c = 0 ……………… (3)
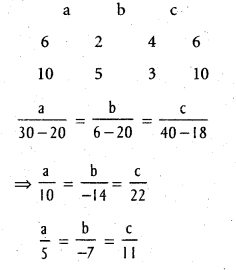
Substituting in (1) equation of the plane ABC is
5x – 7 (y + 1) + 11 (z + 1) = 0
5x – 7y – 7 + 11z + 11 = 0
5x – 7y + 11z + 4 = 0
![]()
Question 3.
Find the equation to the plane parallel to the ZX plane and passing through (0, 4, 4).
Solution:
Equation of ZX plane is y = 0
Equation of the parallel plane is y = k
This plane passes through P(0, 4, 4) = 4 = K
The equation the required plane is y = 4.
Question 4.
Find the equation of the plane through the point, (α, β, γ) and parallel to the plane ax + by + cz = 0.
Solution:
Equation of the given plane is ax + by + cz = 0
Equation of the parallel plane is ax + by+ cz = K
This plane passes through P(α, β, γ)
aα + bβ + cγ = K
∴ Equation of the required plane is
ax + by + cz = aα + bβ + cγ
i.e., a(x – α) + b(y – β) + c(z – γ) = 0
Question 5.
Find the angle between the plane 2x – y + z = 6 and x + y + 2z = 7. [Mar 11]
Solution:
Equation of the planes are
2x – y + z = 6
x + y + 2z = 7
If θ is the angle between the planes, then
cos θ = \(\frac{\left|a_{1} a_{2}+b_{1} b_{2}+c_{1} c_{2}\right|}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}} \sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}\)
= \(\frac{|2.1+(-1) .1+1.2|}{\sqrt{4+1+1} \sqrt{1+1+4}}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\)
= cos π/3
∴ θ = π/3
![]()
Question 6.
Find the equation of the plane passing through (2, 0, 1) and (3, -3, 4) and perpendicular to x – 2y + z = 6.
Solution:
Equation of the plane passing through (2, 0, 1) can be taken as
a(x – 2) + by + c(z – 1) = 0 ……………… (1)
This plane passes through B(3, -3, 4)
a – 3b + 3c = 0 ……………… (2)
The plane (1) is perpendicular to x- 2y + z = 6
a – 2b + c = 0 ………………… (3)

Substituting in (1), equation of the required plane is
3(x – 2) + 2y + 1 (z – 1) = 0
3x – 6 + 2y + z – 1 = 0
3x + 2y + z – 7 = 0
3x + 2y + z = 7.
Question 7.
Let us reduce the equation of the plane x + 2y – 2z – 9 = 0 to the normal form and hence find the direction cosines of the normal to the plane and the length of the perpendicular drawn from the origin to the given plane.
Solution:
The equation of the given plane is
x + 2y – 2z – 9 = 0
Bringing the constant term to R.H.S.
x + 2y – 2z = 9 ………………. (1)
Square root of the sum of the squares of the coefficients of x, y, z in (1) is
\(\sqrt{1^{2}+2^{2}+2^{2}}\) = ±3
dividing (1) by 3, we observe that
p = ± (\(\frac{-9}{3}\)) = ±3
±\(\frac{1}{3}\)x ±\(\frac{2}{y}\)y ±\(\frac{2}{3}\)z = ±3
Choosing the sign of the equation so that the constant on the right is positive, we get,
\(\frac{x}{3}\) + \(\frac{2}{3}\)y – \(\frac{2}{3}\)z = 3 ………………. (2)
(2) represents the equation of the plane in the normal form. Hence d.c.’s of the normal to the plane are (\(\frac{1}{2}\), \(\frac{2}{3}\), –\(\frac{2}{3}\)) and the length of the perpendicular from the origin to the plane is 3.
![]()
Question 8.
Suppose a plane makes intercepts 2, 3, 4 on the X, Y, Z – axes respectively. The equation of the plane whose X, Y, Z intercepts are a, b, c is \(\frac{x}{a}\) + \(\frac{y}{b}\) + \(\frac{z}{c}\) = 1.
Solution:
From the equation of the plane is
\(\frac{x}{2}\) + \(\frac{y}{3}\) + \(\frac{z}{4}\) = 1.
i.e., 6x + 4y + 3z = 12
Question 9.
Consider the plane whose equation is x – 3y + 2z = 9.
Solution:
Dividing by 9, \(\frac{x}{9}\) + \(\frac{y}{-3}\) + \(\frac{z}{9 / 2}\) = 1
Comparing this with \(\frac{x}{a}\) + \(\frac{y}{b}\) + \(\frac{z}{c}\) = 1
a = X-intercept = 9
b = Y-intercept = 3
c = Z-intercept = \(\frac{9}{2}\)