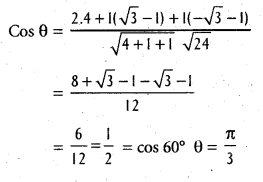Students get through Maths 1B Important Questions Inter 1st Year Maths 1B Direction Cosines and Direction Ratios Important Questions which are most likely to be asked in the exam.
Intermediate 1st Year Maths 1B Direction Cosines and Direction Ratios Important Questions
Question 1.
If P (2, 3, -6), Q (3, -4, 5) are two points, find the d.c.s of \(\overrightarrow{\mathrm{OP}}\), \(\overrightarrow{\mathrm{QO}}\) and \(\overrightarrow{\mathrm{PQ}}\) where O is the origin.
Solution:

Question 2.
Find the d.c.s of a line that makes equal angles with the axes.
Solution:
Suppose the line makes angle a with the axes d.cs of the line are (cos α, cos α, cos α)
But l2 + m2 + n2 = 1
cos2 α + cos2 α + cos2 α = 1
3 cos2 α = 1 ⇒ cos α = \(\frac{1}{3}\)
cos α = ± \(\frac{1}{\sqrt{3}}\)
d.cs of the required line are
(± \(\frac{1}{\sqrt{3}}\), ± \(\frac{1}{\sqrt{3}}\), ± \(\frac{1}{\sqrt{3}}\))
Hence there are 8 such directions which reduce to 4 lines.
![]()
Question 3.
If the d.cs of a line are (\(\frac{1}{c}\), \(\frac{1}{c}\), \(\frac{1}{c}\)) find c.
Solution:
We know that l2 + m2 + n2 = 1
\(\frac{1}{c^{2}}\) + \(\frac{1}{c^{2}}\) + \(\frac{1}{c^{2}}\) = 1, \(\frac{3}{c^{2}}\) = 1 ⇒ c2 = 3
c = ± \(\sqrt{3}\)
Question 4.
Find the direction cosines of two lines which are connected by the relations l + m + n = 0 and mn – 2nl – 2lm = 0. [Mar 11]
Solution:
Given l + m + n = 0 ………………… (1)
mn – 2nl – 2lm = 0 ………………….. (2)
From (1)l = -(m + n)
Substituting in (2)
mn ± 2n (m + n) + 2m (m + n) = 0
mn + 2mn + 2n2 + 2m2 + 2mn = 0
2m2 + 5mn + 2n2 = 0
(2m + n) (m + 2n) = 0
2m = -n or m = -2n
Case (i): 2m1 = -n1
From lr = -m1 – n1
= -m1 + 2m1 = m1
\(\frac{l_{1}}{1}\) = \(\frac{m_{1}}{1}\) = \(\frac{x_{1}}{-2}\)
D.Rs of the first line are 1, 1, -2
D.Cs of this line are \(\frac{1}{\sqrt{6}}\), \(\frac{1}{\sqrt{6}}\), –\(\frac{2}{\sqrt{6}}\)
Case (ii): m2 = -2n2
From (l) l2 = -m2 – n2 = +2n2 – n2 = n2
\(\frac{l_{2}}{1}\) = \(\frac{m_{2}}{-2}\) = \(\frac{n_{2}}{1}\)
d.cs of the second line are 1, -2, 1
d.cs of this line are \(\frac{1}{\sqrt{6}}\), \(\frac{-2}{\sqrt{6}}\), \(\frac{1}{\sqrt{6}}\)
![]()
Question 5.
A ray makes angles \(\frac{\pi}{3}\), \(\frac{\pi}{3}\) with \(\overrightarrow{\mathrm{OX}}\) and \(\overrightarrow{\mathrm{OY}}\) respectively. Find the angle made by it with \(\overrightarrow{\mathrm{OZ}}\).
Solution:
We know that l2 + m2 + n2 = 1
cos2α + cos2β + cos2γ = 1
i.e., cos2 \(\frac{\pi}{3}\) + cos2 \(\frac{\pi}{3}\) + cos2 γ = 1
\(\frac{1}{4}\) + \(\frac{1}{4}\) + cos2 γ = 1
cos2 γ = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)
cos γ = ± \(\frac{1}{\sqrt{2}}\)
γ = cos-1 (± \(\frac{1}{\sqrt{2}}\))
= \(\frac{\pi}{4}\) or \(\frac{3\pi}{4}\).
Question 6.
Find the d.r.s and d.c.s of the line joining the points (4, -7, 3), (6, -5, 2).
Solution:
d.c.s of the lines are (6 – 4, -5 + 7, 2 – 3)
= (2, 2, -1)
Dividing with \(\sqrt{4+4+1}\) = 3
d.cs of the line are ± (\(\frac{2}{3}\), \(\frac{2}{3}\), –\(\frac{1}{3}\)
Question 7.
If the d.c.s of a line are proportional the (1, -2, 1) find its d.c.s.
Solution:
d.rs of the line are (1, -2, 1 )
Dividing with \(\sqrt{6}\)
d.cs of the line are ± (\(\frac{1}{\sqrt{6}}\), –\(\frac{2}{\sqrt{6}}\), \(\frac{1}{\sqrt{6}}\))
![]()
Question 8.
Show that the line joining the points P(0, 1, 2) and Q (3, 4, 8) is parallel to the line joining the points R (-2. \(\frac{3}{2}\). – 3) and S (\(\frac{5}{2}\), 6, 6).
Solution:
DR’s of PQ are (3 – 0, 4 – 1, 8 – 2) = (3, 3, 6)
DR’s of RS are (\(\frac{5}{2}\) + 2, 6 – \(\frac{3}{2}\), 6 + 3)
= (\(\frac{9}{2}\), \(\frac{9}{2}\), 9)
d.r’s of PQ and RS are proportional since \(\frac{2}{3}\) (\(\frac{9}{2}\), \(\frac{9}{2}\), 9) = (3, 3, 6)
∴ PQ is parallel to RS.
Question 9.
Show that the line joining the points A (2, 3, -1) and B(3, 5, -3) is perpendicular to the Line joining C(1, 2, 3) and D(3, 5, 7).
Solution:
d.rs of AB are (3 – 2, 5 – 3, -3 + 1)
= (1, 2, -2)
d.rs of CB are (3 – 1, 5 – 2, 7 – 3) = (2, 3, 4)
a1a2 + b1b2 + c1c2 = 1.2 + 2.3 – 2.4
= 2 + 6 – 8 = 0
∴ AB and CD are perpendicular.
Question 10.
For what value of x the line joining A(4, 1, 2) B (5, x, 0) is perpendicular to the line joining C(1, 2, 3) and D(3, 5, 7) ?
Solution:
d.r’s of AD are (1, x-1, -2)
d.rs of CD are (2, 3, 4)
AB and CD are perpendicular
a1a2 + b1b2 + c1c2 = 0
1.2 – 3(x – 1) + 4 (-2) = 0
2 + 3x – 3 – 8 = 0
3x = 9
⇒ x = 3
![]()
Question 11.
Show that the points A (1, 2, 3), B (4, 0, 4), C(-2, 4, 2) are collinear.
Solution:
d.rs of \(\overline{\mathrm{AB}}\) are 4 – 1, 0 – 2, 3 – 4
i.e., 3, -2, -1
d.rs of \(\overline{\mathrm{BC}}\) are -2 – 4, 4 – 0, 2 – 4
i.e., -6, 4, -2
d.rs of AB and BC are proportional and B is a common point. A, B, C are collinear.
Question 12.
A (1, 8, 4), B (0, -11, 4), C (2, -3, 1) are three points and D is the foot of the perpendicular from A to BC. Find the co-ordinates of D.
Solution:
Suppose divides BC in the ratio m = n
Co-ordinates of D are
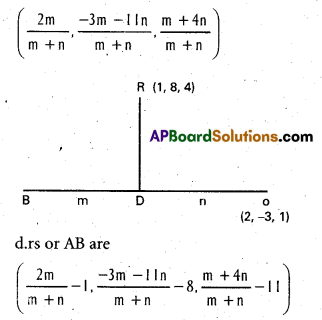
(\(\frac{2 m-m-n}{m+n}\), \(\frac{-3 m-11 n-8 m-8 n}{m+n}\), \(\frac{m+4 n-4 m-4 n}{m+n}\))
\(\frac{m-n}{m+n}\), \(\frac{-11 m-19 n}{m+n}\), \(\frac{-3 m}{m+n}\)
d.rs of BC are (2 – 0, -3 + 11, 1 – 4) = (2, 8, -3)
AB and BC are perpendicular
\(\frac{2(m-n)}{m+n}\) + 8\(\frac{(-11 m-19 n)}{m+n}\) + \(\frac{(-3)(-3 m)}{m+n}\) = 0
2m – 2n – 88m – 152n + 9m = 0
-77m – 154n = 0
77m = -154n
m = -2n
co-ordinates of are
(\(\frac{-4 n}{-n}\), \(\frac{6 n-11 n}{-n}\), \(\frac{-2 n+4 n}{-n}\))
= (4, 5, -2)
![]()
Question 13.
Lines \(\overrightarrow{\mathrm{OA}}\), \(\overrightarrow{\mathrm{OB}}\) are drawn from O with direction cosines proportional to (1, -2, -1), (3, -2, 3). Find the direction cosines of the normal to the plane AOB.
Solution:
Suppose l, m, n are the d.cs of the normal.
It is perpendicular to every line in the plane AOB
l – 2m – n = 0
3l – 2m + 3n = 0
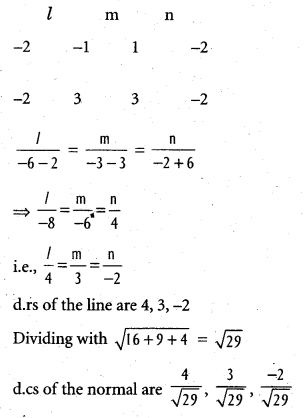
Question 14.
Find the angle between the diagonals of a cube.
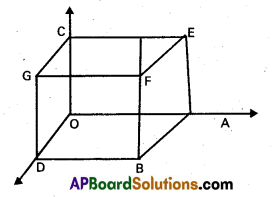
Solution:
Let ‘O’ one of the vertices of the cube taken as origin and the three sides OA, OB, OC are taken as co-ordinate axes. Let OA = OB = OC = a the four diagonals are \(\overrightarrow{\mathrm{OF}}\), \(\overrightarrow{\mathrm{AG}}\), \(\overrightarrow{\mathrm{DE}}\) and \(\overrightarrow{\mathrm{BC}}\)
The co-ordinates of the vertices of the cube are 0(0, 0, 0), A(a, 0, 0), B(0, a, 0), C(0,0, a), F(a, a, 0), D(a, a, 0), E(a, 0, a), G(0, a, a)
D.Rs of OF are (a-0, a – 0, a – 0) = (a, a, a)
D.Rs of AG are (0 – 9, a – 0, a – 0) = (-a, a, a)
If O is the angle between the diagonals OF and AG then
cos θ = \(\frac{|a(-a)+a \cdot a+a \cdot a|}{\sqrt{a^{2}+a^{2}+a^{2}} \cdot \sqrt{a^{2}+a^{2}+a^{2}}}\)
= \(\frac{a^{2}}{3 a^{2}}\) = \(\frac{1}{3}\)
θ = Cos-1 (\(\frac{1}{3}\))y
Similarly, the angle between any pair of diagonals can be shown to be cos-1 (\(\frac{1}{3}\))
![]()
Question 15.
Show that the line whose d.c’s are proportional to (2, 1, 1) (4, \(\sqrt{3}\) -1, –\(\sqrt{3}\) – 1) are inclined to one another at angle \(\frac{\pi}{3}\).
Solution:
The d.cs of the given lines are (2, 1, 1), (4, \(\sqrt{3}\) – 1, –\(\sqrt{3}\) – 1) 42 + (\(\sqrt{3}\) – 1)2 + (-\(\sqrt{3}\) – 1)2
= 16 + 3 + 1 – 2\(\sqrt{3}\) + 3 + 1 + 2\(\sqrt{3}\)
= 24