Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B The Straight Line Solutions Exercise 3(b) will help students to clear their doubts quickly.
Intermediate 1st Year Maths 1B The Straight Line Solutions Exercise 3(b)
I.
Question 1.
Find the sum of the squares of the inter¬cepts of the line 4x – 3y = 12 on the axes, of co-ordinates.
Solution:
Equation of the given line is
\(\frac{4 x}{12}-\frac{3 y}{12}=1\)
\(\frac{x}{3}+\frac{y}{-4}=1\)
a = 3, b = -4
Sum of the squares = a² + b²
= 9 + 16 = 25
Question 2.
If the portion of a straight line inter¬cepted between the axes of co-ordinates is bisected at (2p, 2q), write the equation of the straight line.
Solution:
Equation of AB in the intercept form is
\(\frac{x}{a}+\frac{y}{b}=1\) …………… (1)
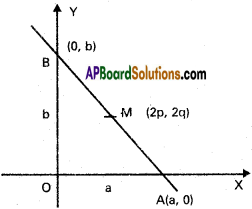
Co-ordinates of A are (a, 0) and B are (0, b)
M is the mid-point of AB
Co-ordinates of M are (\(\frac{a}{2}\), \(\frac{b}{2}\)) = (2p, 2q)
\(\frac{a}{2}\) = 2p, \(\frac{b}{2}\) = 2q
a = 4p, b = 4q
Substituting in (1), equation of AB is
\(\frac{x}{4 P}+\frac{y}{4 Q}=1\)
\(\frac{x}{P}+\frac{y}{Q}=4\)
Question 3.
If the linear equation ax + by + c = 0
(a,b,c ≠ 0) and lx + my + n = 0
represent the same line and r = \(\frac{l}{a}\) = \(\frac{n}{c}\)
write the value of r in terms of m and b.
Solution:
ax + by + c — 0 and
lx + my + n = 0 represent the same line
∴ \(\frac{1}{a}=\frac{m}{b}=\frac{n}{c}=r\)
\(\frac{m}{b}\) = r
![]()
Question 4.
Find the angle made by the straight line y = – √3x + 3 with the positive direction of the X-axis mea-sured in the counter clock-wise direction.
Solution:
Equation of the given line isy = -√3x + 3 Suppose a is the angle made by this line with positive X – axis in the counter clock – wise direction.
tan α = – √3 = tan \(\frac{2 \pi}{3}\)
α = \(\frac{2 \pi}{3}\)
Question 5.
The intercepts of a straight line on the axes of co-ordinates are a and b. If p is the length of the perpendicular drawn from the origin to this line. Write the value of p in terms of a and b.
Solution:
Equation of the line in the intercept form is
p = length of the perpendicular from origin

II.
Question 1.
In what follows, p denotes the distance of the straight line from the origin and a denotes the angle made by the normal ray drawn from the origin to the straight line with \(\stackrel{\leftrightarrow}{O X}\) measured in the anticlockwise sense. Find the equations of the straight lines with the following values of p and a.
i) p = 5, a = 60°
ii) p = 6, a = 150°
iii) p = 1, α = \(\frac{7 \pi}{4}\)
iv) p = 4, α = 90°
v) p = 0, α = 0
vi) p = 2√2, α = \(\frac{5 \pi}{4}\)
Solution:
Equation of the line in the normal form is x cos α + y sin α = p
i) p = 5, α = 60°
cos α = cos 60° = \(\frac{1}{2}\)
sin α = sin 60° = \(\frac{\sqrt{3}}{2}\)
Equation of the line is x. \(\frac{1}{2}\) + y. \(\frac{\sqrt{3}}{2}\) = 5
⇒ x + √3y= 10
ii) p = 6, α = 150°
cos α = cos 150° = cos (180° – 30°)
= -cos 30° = – \(\frac{\sqrt{3}}{2}\)
sin α = sin 150°
= sin (180° – 30°)
= sin 30° = \(\frac{1}{2}\)
Equation of the line is
x.(-\(\frac{\sqrt{3}}{2}\)) + y.\(\frac{1}{2}\) = 6
-√3x + y = 12
or √3x – y + 12 = 0
iii) p = 1, α = \(\frac{7 \pi}{4}\)
cos α = cos 315° = cos (360° – 45°)
= cos 45° = \(\frac{1}{\sqrt{2}}\)
sin α = sin 315° = sin (360° – 45°)
= -sin45° = \(\frac{1}{\sqrt{2}}\)
Equation of the line is
x.\(\frac{1}{\sqrt{2}}\) – y.\(\frac{1}{\sqrt{2}}\) = 1
x – y = √2
x – y – √2 = 0
iv) p = 4, α = 90°
cos α = cos 90° = 0, sin α = sin 90° = 1
Equation of the line is
x.0 + y.1 = 4
y = 4
v) p = 0, α = 0
cos α = cos 0 = 1, sin α = sin 0 = 0
Equation of the line is
x.1 + y.0 = 0
x = 0
vi) p = 2√2 , α = \(\frac{5 \pi}{4}\)
cos α = cos 225° = cos (180° + 45°)
= -cos 45° = – \(\frac{1}{\sqrt{2}}\)
sin α = sin 225° = sin (180° + 45°)
=-sin 45° = – \(\frac{1}{\sqrt{2}}\)
Equation of the line is
x(-\(\frac{1}{\sqrt{2}}\)) + y(-\(\frac{1}{\sqrt{2}}\)) = 2√2
– x – y = 4
or x + y + 4 = 0
![]()
Question 2.
Find the equations of the straight line in the symmetric form, given the slope and a point on the line in each part of the question.
i) √3, (2, 3)
ii) –\(\frac{1}{\sqrt{3}}\), (-2, 0)
iii) -1, (1,1)
Solution:
i) Equation of the line in the symmetric form is
\(\frac{x-x_{1}}{\cos \alpha}=\frac{y-y_{1}}{\sin \alpha}=r\)
(x1, y1) = (2, 3)
m = tan α = √3 ⇒ α = 60°
cos α = cos 60° = \(\frac{1}{2}\)
sin α = sm 60° = \(\frac{\sqrt{3}}{2}\)
Equation of the line in symmetric form is
\(\frac{x-2}{\cos \frac{\pi}{3}}=\frac{y-3}{\sin \frac{\pi}{3}}\)
ii) (x1, y1) = (-2, 0)
tan α = –\(\frac{1}{\sqrt{3}}\) ⇒ α = 180° – 30° = 150°
Equation of the line is \(\frac{x+2}{\cos 150^{\circ}}=\frac{y}{\sin 150^{\circ}}\)
iii) tan α = -1, α =180°- 45° = 135°
(x1, y1) = (1, 1)
Equation of the line is \(\frac{x-1}{\cos \left(\frac{3 \pi}{4}\right)}=\frac{y-1}{\sin \left(\frac{3 \pi}{4}\right)}\)
Question 3.
Transform the following equation into
a) Slope-intercept form
b) Intercept form and
c) Normal form
i) 3x + 4y = 5
ii) 4x – 3y + 12 = 0
iii) √3x + y = 4
iv) x + y + 2 = 0
v) x + y – 2 = 0
vi) √3x + y + 10 = 0
Solution:
i) 3x + 4y = 5
Slope-intercept form
4y = -3x + 5
\(y=\left(-\frac{3}{4}\right) x+\left(\frac{5}{4}\right)\)
Intercept form :
3x + 4y = 5

x cos α + y sin α = 1
ii) 4x – 3y + 12 = 0
Slope-intercept form :
3y = 4x + 12
y = (\(\frac{4}{3}\))x + 4
Intercept form:
4x – 3y+ 12 = 0
-4x + 3y = 12
\(\frac{-4 x}{12}+\frac{3 y}{12}=1\)
\(\frac{x}{(-3)}+\frac{y}{4}=1\)
Normal form :
4x – 3y + 12 = 0
– 4x + 3y = 12

x cos α + y sin α = \(\frac{12}{5}\)
iii) √3x + y = 4
Slope-intercept form :
√3x + y = 4
y = -√3x + 4
Intercept form :
√3x + y = 4

iv) x + y + 2 = 0
Slope-intercept form
x + y+.2 = 0
y = -x – 2
= (-1)x + (-2)
Intercept form:
x + y + 2 = 0
-x – y = 2
\(\frac{x}{(-2)}+\frac{y}{(-2)}=1\)
Normal form:
x + y + 2 = 0
-x – y = 2
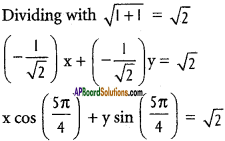
v) x + y – 2 = 0
Slope-intercept form :
x + y – 2 = 0
y = – x + 2
Intercept form:
x + y – 2 = 0
x + y = 2
\(\frac{x}{2}+\frac{y}{2}\) = 1
Normal form :
x + y-2 = 0
x + y = 2
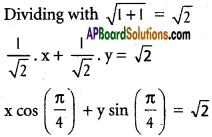
vi) √3x + y + 10 = 0
Slope-intercept form :
√3x + y + 10 = 0
y = -√3x – 10
Intercept form :
√3x + y = -10
Normal form :
√3x + y = -10
Dividing with \(\sqrt{3+1}=2\), we get
\(\frac{-\sqrt{3}}{2} \cdot x+\frac{-1}{2} \cdot y=5\)
x cos 30° + y sin 30° = 5
Question 4.
If the product of the intercepts made by the straight line x tan α + y sec α = 1 (0 ≤ α < \(\frac{\pi}{2}\)), on the co-ordinate axes is equal to sin α, find α.
Solution:
Equation of the line is x tan α + y sec α = 1
\(\frac{x}{\cot \alpha}+\frac{y}{\cos \alpha}=1\)
a = cot α, b = cos α
Given ab = sin α
cot α. cos α = sin α
\(\frac{\cos ^{2} \alpha}{\sin \alpha}\) = sin α ⇒ cos² α = sin α
tan² α = 1 ⇒ tan α = ±1
α = 45°
![]()
Question 5.
If the sum of the reciprocals of the intercepts made by a variable straight line on the axes of co-ordinate is a constant, then prove that the line always passes through a fixed point.
Solution:
Equation of the line in the intercept form is
\(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\) ………….. (1)
Sum of the reciprocals of the intercepts
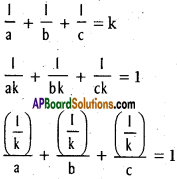
The line (1) passes through the fixed point
\(\left(\frac{1}{k}, \frac{1}{k}, \frac{1}{k}\right)\)
Question 6.
Line L has intercepts a and b on the axes of coordinates. When the axes are rota¬ted through a given angle, keeping the origin fixed, the same line L has intercepts p and q on the transformed axes. Prove that \(\frac{1}{a^{2}}+\frac{1}{b^{2}}=\frac{1}{P^{2}}+\frac{1}{Q^{2}}\).
Solution:
Equation of the line in the old system in the intercept form is
\(\frac{x}{a}+\frac{y}{b}=1 \Rightarrow \frac{x}{a}+\frac{y}{b}-1=0\)
Length of the perpendicular from origin

Equation of the line in the second system in the intercept form is
\(\frac{x}{p}+\frac{y}{Q}=1 \Rightarrow \frac{x}{p}+\frac{y}{Q}-1=0\)
Length of the perpendicular from origin
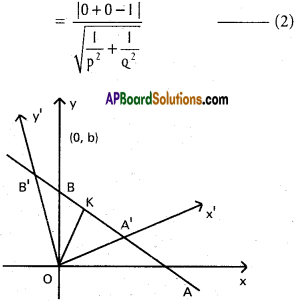
Since the origin and the given line remain unchanged we have from (1) and (2)

Question 7.
Transform the equation \(\frac{x}{a}+\frac{y}{b}=1\) into the normal form when a > 0 and b > 0. If the perpendicular distance of the straight line from the origin is p, deduce that \(\frac{1}{p^{2}}=\frac{1}{a^{2}}+\frac{1}{b^{2}}\).
Solution:

III.
Question 1.
A straight line passing through A(-2, 1) makes an angle 30° with \(\overrightarrow{O X}\) in the positive direction. Find the points on the straight line whose distance from A is 4 units.
Solution:
Co-ordinates of any point on the given line are (x1 + r cos α, y1 + r sin α)
α = 30° ⇒ cos α = cos 30° = \(\frac{\sqrt{3}}{2}\),
sin α = sin = 30° = \(\frac{1}{2}\)
(x1, y1) = (-2, 1) ⇒ x1 = -2 y1 = 1
Taking r = 4 ⇒ co-ordinates of P are

Question 2.
Find the points on the line 3x – 4y – 1 = 0 which are at a distance of 5 units from the point (3, 2).
Solution:
Equation of the line in the symmetric form is
\(\frac{x-3}{\cos \alpha}=\frac{y-2}{\sin \alpha}=r\)
Co-ordinates of the point P are
(3 + r cos α, 2 + r sin α) = (3 + 5 cos α, 2 + 5 sin α)
P is a point on 3x – 4y – 1 = 0
3(3 + 5 cos α) – 4(2 + 5 sin α) -1 = 0
9 + 15 cos α – 8 – 20 sin α – 1 = 0
15 cos α – 20 sin α = 0
15 cos α = + 20 sin α
tan α = + T
Case i) : cos α = +\(\frac{4}{5}\), sin α \(\frac{3}{5}\)
Case ii) : cos α = –\(\frac{4}{5}\), sin α \(\frac{3}{5}\)
Case i) : Co-ordinates of P are
\(\left(3+5 \cdot \frac{4}{5}, 2+5 \cdot \frac{3}{5}\right)=(7,5)\)
Case ii) : Co-ordinates of P are
\(\left(3-5 \cdot \frac{4}{5}, 2-5 \cdot \frac{3}{5}\right)=(-1,-1)\)
![]()
Question 3.
A straight line whose inclination with the positive direction of the X-axis measured in the antidock wise sense is it/3 makes positive intercept on the Y-axis. If the straight line is at a distance of 4 from the origin, find its equation.
Solution:
Given α = π/3, p = 4
m = tan α = tan 60° = √3
Equation of the line in the slope – intercept form is
y = √3 x + c
√3x – y + c = 0
Distance from the origin = 4
\(\frac{|0-0+c|}{\sqrt{3+1}}=4\)
|c| = 4 × 2 = 8
c = ± 8
Given c > 0 ∴ c = 8
Equation of the line is √3x – y + 8 = 0
Question 4.
A straight line L is drawn through the point A (2, 1) such that its point of intersection with the straight line x + y = 9 is at a distance of 3√2 from A. Find the angle which the line L makes With the positive direction of the X – axis.
Solution:
Suppose a is the angle made by L with the positive X – axis
Any point on the line is
(x1 + r cos α1, y1 + r sin α) = (2 + 3√2 cos α 1 + 3√2 sin α)
This is a point on the line x + y = 9
2+ 3√2 cos α+ 1 + 3√2 sin α = 9
3√2 (cos α + sin α) = 6
cos α + sm α = \(\frac{6}{3 \sqrt{2}}\) = √2
\(\frac{1}{\sqrt{2}}\). cos α + \(\frac{1}{\sqrt{2}}\) sin α = 1
cos α. cos 45° + sin α. sin 45° = 1
cos (α – 45°) = cos 0°
α – 45° = 0 ⇒ α = 45° = \(\frac{\pi}{3}\)
![]()
Question 5.
A straight line L with negative slope passes through the point (8, 2) and cuts positive co-ordinate axes at the points P and Q. Find the minimum value of OP + OQ as L varies, when O is the origin.
Solution:
Equation of the line passing through A(8, 2) with negative slope ‘-m’ is y – 2 = -m(x – 8)
mx + y – (2 + 8m) = 0
mx + y = 2 + 8m

OP =X Intercept = \(\frac{2+8 m}{m}\)
OQ = Y – Intercept = 2 + 8m 2 + 8m

For f(m) to have minimum or maximum, we must have f'(m) = 0

and ‘f’ has minimum at m = \(\frac{1}{2}\)
∴ Minimum value of f(m) = Minimum Value I of OP + OQ at m = \(\frac{1}{2}\)
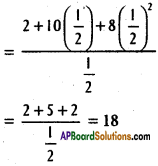
∴ Minimum value of OP + OQ as L varies, where ‘O’ is the origin is 18.