Inter 1st Year Maths 1B The Straight Line Solutions Ex 3(c)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B The Straight Line Solutions Exercise 3(c) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B The Straight Line Solutions Exercise 3(c)

I.

Question 1.
Find the ratio in which the following straight lines divide the line segment joining the given points. State whether the points lie on the same side or on either side of the straight line, i) 3x – 4y = 7, (2, -7) and (-1, 3)
Solution:
3x – 4y – 7= 0

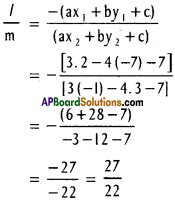
L₁₁, L₂₂ are of opposite signs. The given points lie on opposite sides of the line.

ii) 3x + 4y = 6, (2, -1) and (1, 1)
Solution:
Equation of the line is 3x + 4y – 6 = 0

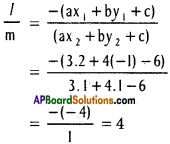
The points lie on the opposite side of the line.

iii) 2x + 3y = 5, (0, 0) and (-2, 1)
Solution:
\(\frac{I}{m}=\frac{-(0+0-5)}{-4+3-5}\)
\(\frac{-5}{6}\)
The points lie on same side of the line.

Question 2.
Find,the point of intersection of the follow- ing lines.
i) 4x + 8y – 1 = 0, 2x – y + 1 = 0
Solution:
4x + 8y – 1 = 0, 2x – y + 1 = 0
point of intersection is

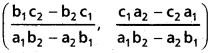
ii) 7x + y + 3 = 0, x + y = 0
Solution:
7x + y+ 3 = 0, x + y = 0 x y 1

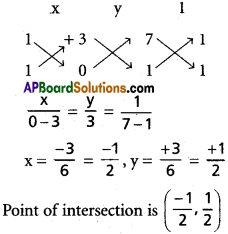
Question 3.
Show that the straight lines (a – b) x + (b – c) y = c – a, (b – c)x + (c – a) y = (a – b) and (c – a)x + (a – b) y = b – c are concurrent.
Solution:
Equations of the given lines are
(a – b) x + (b – c) y = c – a …………… (1)
(b – c) x +(c – a) y = a – b …………… (2)
(c – a) x + (a – b) y = b – c …………… (3)
From (1) and (2)


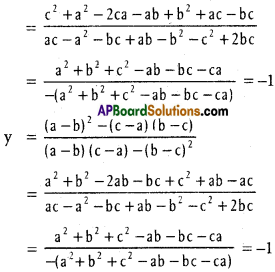
Point of intersection of (1) and (2) is P (-1, -1)
Substituting in (3)
(c – a) (-1) + (a – b) (-1) = -c + a – a + b = b – c
∴ P (-1, -1) is a point on (3)
The given lines are concurrent.

Question 4.
Transform the following equation into the form L₁ + λL₂ = 0 and find the point of concurrency of the family of straight lines represented by the equation.
i) (2 + 5k) x – 3(1 + 2k)y + (2 – k) = 0
Solution:
(2 + 5k)x – 3(1 + 2k)y + (2 – k) = 0
(2x – 3y + 2) + k (5x – 6y – 1) = 0
This is of the form L₁ + λL₂ = 0
L₁ = 2x – 3y + 2 = 0
L₂ = 5x – 6y – 1 = 0

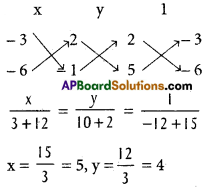
The point of concurrency is P (5, 4).

ii) (k + 1) x + (k + 2) y + 5 = 0
Solution:
(k + 1) x + (k + 2) y + 5 = 0
k (x + y) + (x + 2y + 5) = 0
i.e., (x + 2y + 5) + k (x + y) = 0
This is of the form L₁ + λL₂ = 0
∴ L₁ = x + 2y + 5 = 0
L₂ = x + y = 0

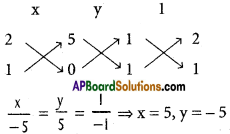
Point of concurrency is P (5, – 5).

Question 5.
Find the value of P, If the straight lines. x + p = 0, y + 2 = 0 and 3x + 2y + 5 = 0 are concurrent.
Solution:
Equations of the given lines are
x + p = 0 …………. (1)
y + 2 = 0 …………. (2)
3x + 2y + 5 = 0 …………. (3)
From (2), y = -2
Substituting in (3)
3x – 4 + 5 = 0
3x = 4 – 5 = -1
x = –\(\frac{1}{3}\)
Point of intersection of (2) and (3) is P (-\(\frac{1}{3}\), – 2)
The given lines are concurrent
P is a point on x + p = 0
–\(\frac{1}{3}\) + p = o ⇒ p = \(\frac{1}{3}\)

Question 6.
Find the area of the triangle formed by the following straight lines and the coordinate axes,
i) x – 4y + 2 = 0
Solution:
Equation of AB is
x – 4y + 2 = 0
– x + 4y = 2
\(\frac{x}{-2}+\frac{y}{\left(\frac{1}{2}\right)}=1\)
a = -2 b = \(\frac{1}{2}\)
Area of ∆OAB = \(\frac{1}{2}\)|ab|
= \(\frac{1}{2}\)|-2 × \(\frac{1}{2}\)| = \(\frac{1}{2}\) sq.units

ii) 3x – 4y + 12 = 0
Solution:
Equation of AB is
3x – 4y + 12 = 0
– 3x + 4y = 12
\(\frac{x}{-4}+\frac{y}{3}\) = 1
Area of ∆OAB = \(\frac{1}{2}\)|ab|
= \(\frac{1}{2}\)|(-4) (3)| = \(\frac{1}{2}\)(12)
= 6 sq. units

II.

Question 1.
A straight line meets the co-ordinate axes at A and B. Find the equation of the straight line, when
i) \(\overline{\mathrm{AB}}\) is divided in the ratio 2:3 at (-5, 2).

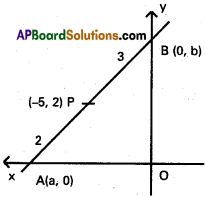
Solution:
Let OA = a and OB = b
Co-ordinates of A are (a, 0) and B are (0, b)
P divides AB in the ratio 2:3

-3x + 5y = 25
3x – 5y + 25 = 0

ii) \(\overline{\mathrm{AB}}\) is divided in the ratio 1:2 at (-5,4)
Solution:
Let OA = a and OB = b
Co-ordinates of A are (a, 0) and B are (0, b)
P divides AB in the ratio 1 : 2

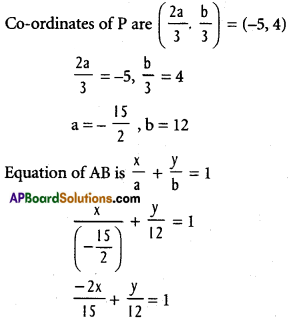
– 8x + 5y = 60
8x – 5y + 60 = 0

iii) (p, q) bisects \(\overline{\mathrm{AB}}\)
Solution:
Let OA a and OB = b
Co-ordinates of A are (a, 0) and B are (0, b)

Question 2.
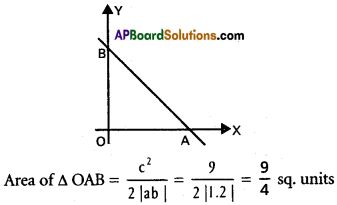
Find the equation of the straight line passing through the points (-1, 2) and (5, -1) and also find the area of the triangle formed by it with the axes of coordinates.
Solution:
P (-1, 2) and Q (5, -1) are the given points. Equation of
PQ is (y – y₁) (x₁ – x₂) = (x – x₁) (y₁ – y₂)
(y – 2) (-1 -5) = (x + 1) (2 + 1)
-6 (y – 2) = 3 (x+ 1)
-2y + 4 = x+ 1
x + 2y – 3 = 0

Question 3.
A triangle of area 24 sq. units is formed by a straight line and the co-ordinate axes is the first quadrant. Find the equation of the straight line, if it passes through (3, 4).

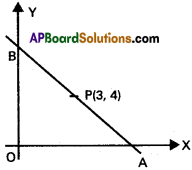
Solution:
Equation of AB in the
intercept form is \(\frac{x}{a}+\frac{y}{b}\) = 1
This line passes through P (3, 4)

Area of ∆ OAB = 24 ⇒ \(\frac{1}{2}\) |ab|= 24
\(\frac{1}{2} \frac{4 a^{2}}{a-3}=24\)
a² = 12 (a – 3)
= 12a – 36
a² – 12a + 36 = 0
(a – 6)² = 0 ⇒ a = 6
b = \(\frac{4a}{a-3}=\frac{24}{3}\) = 8
Equation of AB is \(\frac{x}{6}+\frac{y}{8}\) = 1
4x + 3y = 24
4x + 3y – 24 = 0

Question 4.
A straight line with slope 1 passes through Q(-3, 5) and meets the straight line x + y – 6 = 0 at P. Find the distance PQ.

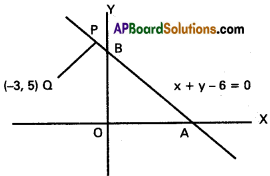
Solution:
Given slope = 1
tan α = 1 = tan 45°
α = 45°
The line passes through Q (-3, 5)
Co-ordinates of P are (x₁ + r cos α, y₁ + r sin α)
= (-3 + r cos 45°, 5 + r sin 45°)

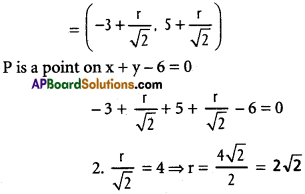
PQ = 2√2

Question 5.
Find the set of values of ‘a’ if the points (1, 2) and (3, 4) lie to the same side of the straight line 3x – 5y + a = 0
Solution:
P (1, 2), Q (3, 4) are the given points.
Equation of the given line is 3x – 5y + a = 0
L₁₁ = 3.1 – 5.2 + a = a – 7
L₂₂ = 3.3 – 5.4 + a = a – 11
a – 7 and a – 11 must both be positive or both negative.

Case (i) :
a – 7 > 0, a – 11 > 0
a > 7 and a > 11
∴ a > 7.11 ⇒ a∈ (11, α)

Case (ii) :
a – 7 < 0, a – 17 < 0
a < 7, a < 17
⇒ a < 17, ⇒ a∈ (-α, 27)
∴ a ∈ (-α, 7) U (11, α)

Question 6.
Show that the lines 2x + y – 3 = 0,
3x + 2y – 2 = 0 and 2x – 3y – 23 = 0 are concurrent and find the point of concurrency.
Solution:
Equations of the given lines are
2x + y – 3 = 0 ……………. (1)
3x + 2y – 2 = 0 ……………. (2)
2x – 3y – 23 = 0 ……………. (3)

From (1) and (2)

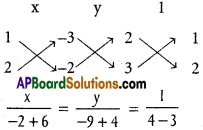
x = 4, y = – 5
Co-ordinates of P are (4, -5)
2x – 3y – 23 = 2(4) – 3(-5) – 23
= 8 + 15 – 23 = 0
P lies on (3)
The given lines are concurrent Point of concurrency is P (4, -5)

Question 7.
Find the value of p, if the following lines are concurrent.
(i) 3x + 4y = 5, 2x + 3y = 4, px + 4y = 6
(ii) 4x – 3y – 7 = 0, 2x + py + 2 = 0, 6x + 5y – 1 = 0
Solution:
(i) Equations of the lines are
3x + 4y – 5 = 0
2x + 3y – 4 = 0

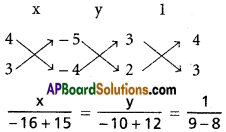
x = -1, y = 2

Point of intersection of (1) and (2) is P (-1, 2)
The given lines are concurrent.
P lies on px + 4y = 6
-p + 8 = 6 ⇒ p = 8- 6 = 2

(ii) Equations of the lines
4x – 3y – 7 = 0
6x + 5y- 1 = 0

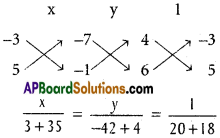
x = 1, y = -1
Co-ordinates of P are (1, -1)
The given lines are concurrent.
P is a point on
2x + py + 2 = 0
2 – p + 2 = 0
p = 4

Question 8.
Determine whether or not the four straight lines with equations
x + 2y – 3 = 0, 3x + 4y – 7 = 0,
2x + 3y – 4 = 0 and 4x + 5y – 6 = 0 are concurrent.
Solution:
Equations of the given lines are
x + 2y – 3 = 0 ………. (1)
3x + 4y – 7 = 0 ………. (2)
2x + 3y – 4 = 0 ………. (3)
4x + 5y – 6 = 0 ………. (4)
Solving (1) and (2)

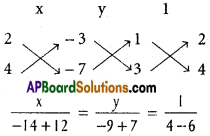
x = 1, y = 1
Point of intersection of (1) and (2) is P (1, 1)
2x + 3y – 4 = 2.1 + 3.1 – 4 = 5 – 4 = 1 ≠ 0
4x + 5y- 6 = 4.1 + 5.1 – 6 = 9 – 6 = 3 ≠ 0
∴ P (1,1) is not a point on (3) and (4)
∴ The given lines are not concurrent.

Question 9.
If 3a + 2b + 4c = 0, then show that the equation ax + by + c = 0 represents a family of concurrent straight lines and find the point of concurrency.
Solution:
Given condition is 3a + 2b + 4c = 0
\(\frac{3}{4}\)a + \(\frac{1}{2}\)b + c = 0
For all values of a, b the line ax + by + c = 0
passes through the point (\(\frac{3}{4}\), \(\frac{1}{2}\))
The equation ax + by + c = 0 represents a family of concurrent lines.
Point of concurrency is (\(\frac{3}{4}\), \(\frac{1}{2}\))

Question 10.
If non-zero numbers a, b, c are in harmonic progression then show that the equation \(\frac{x}{a}+\frac{y}{b}+\frac{1}{c}\) = o represents a family of concurrent lines and find the point of concurrency.
Solution:
Given a, b, c are in H.P.
∴ \(\frac{2}{b}=\frac{1}{a}+\frac{1}{c}\)
\(\frac{1}{a}+\frac{(-2)}{b}+\frac{1}{c}\) = o
∴ For all values of a,b,c the equation \(\frac{x}{a}+\frac{y}{b}+\frac{1}{c}\) = o
represents a line passing through the point (1, -2)
∴ The equation, \(\frac{x}{a}+\frac{y}{b}+\frac{1}{c}\) = o represents a family of concurrent lines.
Point of concurrency is P (1, – 2)

III.

Question 1.
Find the point on the straight lines
3x + y 4- 4 = 0 which is equidistant from the points (-5, 6) and (3, 2).
Solution:
P(x₁, y₁) is the point on 3x + y + 4 = 0
3x₁ + y₁ + 4 = 0 …………. (1)
Given PA = PB ⇒ PA² = PB²

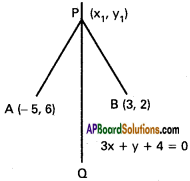
(x₁+ 5)² + (y₁ – 6)² = (x₁ – 3)² + (y₁ – 2)²
x²₁ + 10x₁ + 25 + y²₁ – 12y₁ + 36 = x²₁ -6x₁ + 9 + y²₁ – 4y₁ + 4
16x₁ – 8y₁ + 48 = 0
2x₁ – y₁+ 6 = 0 ……….. (2)
3x₁ + y₁ +4 = 0 ………… (1)
Adding 5x₁ + 10 = 0 ⇒ x₁ = – 2
From (1) – 6 + y₁ + 4 = 0
y₁ = 6 – 4 = 2
Co-ordinates of P are (-2, 2)

Question 2.
A straight line through P (3, 4) makes an angle of 60° with the positive direction of the X-axes. Find the co-ordinates of the points on that line which are 5 units away from P.
Solution:
Co-ordinates of any point on the line Q are (x₁ + r cos θ, y₁ + r sin θ)
Given (x₁, y₁) = (3, 4) i.e., x₁ = 3, y₁ = 4
θ = 60° ⇒ cos θ = cos 60° = \(\frac{1}{2}\), sin θ = sin 60° \(\frac{\sqrt{3}}{2}\)

Question 3.
A straight line through Q (√3, 2) makes an angle \(\frac{\pi}{6}\) with the positive direction of the X-axis. If the straight line intersects the line √3x – 4y + 8 = 0 at P; find the distance of PQ.
Note : AB and PQ are not perpendicular.
So we have to follow the first method only.
Solution:

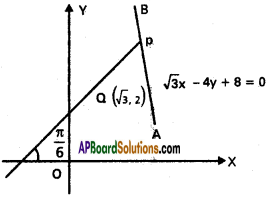
PQ makes an angle \(\frac{\pi}{6}\) with the positive direction of X – axis.
m = Slope of PQ = tan 30° = \(\frac{1}{\sqrt{3}}\)
PQ passes through Q (√3, 2)
Equation of PQ is y – 2 = \(\frac{1}{\sqrt{3}}\)(x – √3)
√3y – 2√3 = x – √3
x – √3y = – √3 ………… (1)
Equation of AB is √3x – 4y + 8 = 0
√3x – 4y = -8 ……………. (2)
(1) × √3 ⇒ √3x – 3y = -3
Subtracting -y = -5
y = 5
From (1), x = √3y – √3
= 5√3 – √3 = 4√3
Equation of AB is
Co-ordinates of P are ( 4√3, 5)
Q are (√3, 2)
PQ²= (4√3 – √3)² +(5 – 2)²
= 27 + 9 = 36
PQ =6 units.

Question 4.
Show that the origin is with in the triangle whose angular points are (2,1), (3,-2) and (-4,-1).
Solution:
The vertices of the ∆ le ABC are
A = (2, 1), B = (3, -2), C = (-4, -1)

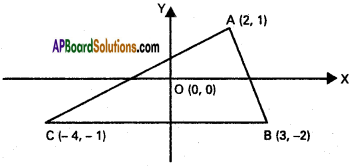
The equation of BC is

⇒ 7y + 7 = -x -4
L = x + 7y + 11 = 0 …………. (1)
The equation of CA is

⇒ 3y + 3 = x + 4
⇒ L’ = x – 3y + 1 = 0 ………. (2)

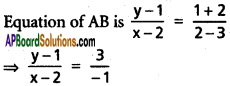
⇒ 3x – 6 = -y + 1
L” = – 3x + y – 7 = 0 …………… (3)
L” (- 4, -1)= 3 (- 4) – 1 – 7
= – 20 is negative.
L” (0,0) = 3(0) + 0 – 7
= – 7 is negative
So (- 4, -1), (0,0) lie on the same side of AB
Hence O (0,0) lies to the left of AB ………… (4)
L’ (3, -2) = 3 – 3 (- 2) + 1
= 10 is positive

L” (0, 0) =0 – 3 (0) + 1
= 1 is positive
So (0, 0), (3, -2) lie on the same side of AC
both down of AC ………… (5)
L (2, 1) = 2 + 7(1) + 11
= 20 is positive

L (0, 0) =0 + 7(0)+ 11
= 11 is positive
So (0, 0) and (2, 1) lie on the same side of BC.
So (0, 0) lie upwards from BC ……… (6)

From (4), (5), (6) it follows O (0,0) lies down-wards of AC, upwards of BC, and to the left of AB. So O (0, 0) will lie inside the ∆ ABC.

Question 5.
A straight line through Q(2, 3) makes an angle \(\frac{3 \pi}{4}\) with negative direction of the X – axis. If the straight line intersects the line x+ y – 7 = 0 at P, find the distance PQ.

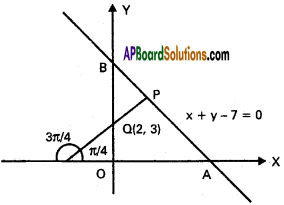
Solution:
The line PQ makes an angle \(\frac{3 \pi}{4}\) with the negative direction of X – axis i.e., PQ makes and angle π – \(\frac{3 \pi}{4}\) = \(\frac{\pi}{4}\) with the positive direction of X – axis.
Co-ordinates of Q are (2, 3)
Co-ordinates of P are (x₁ + r cos θ, y₁ + r sin θ)

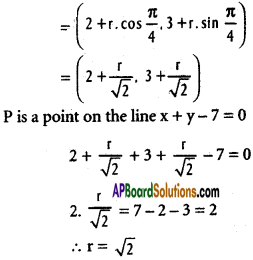
PQ = r = √2 units.

Question 6.
Show that the straight lines x + y = 0, 3x + y – 4 = 0 and x + 3y – 4 = 0 form an isosceles triangle.
Solution:
Given lines
x + y = 0 ………….. (1)
3x + y – 4 = 0 ………….. (2)
x + 3y – 4 = 0 ………….. (3)
Let θ₁ be the angle between (1), (2)

Let θ₂ be the angle between (2), (3)

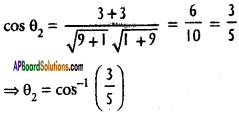
Let 0, be the angle between (3), (1)

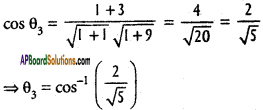
Since θ₁ = θ₃
∴ The ∆^le formed by the lines is an Isosceles triangle.

Question 7.
Find the area of the triangle formed by the straight lines 2x – y – 5 = 0, x – 5y + 11 = 0 and x + y – 1 = 0.
Solution:
Given lines
2x – y – 5 = 0 ………….. (1)
x – 5y + 11 =0 …………. (2)
x + y – 1 = 0 ………….. (3)
By solving (1), (2)

Let A = (4, 3)
By solving (2), (3)

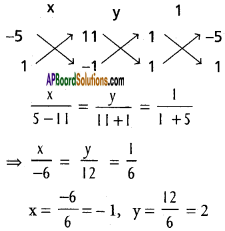
∴ B = (- 1,2)
By solving (3), (1)

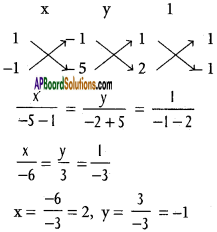
∴ C = (2, -1)