Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Transformation of Axes Solutions Exercise 2(a) will help students to clear their doubts quickly.
Intermediate 1st Year Maths 1B Transformation of Axes Solutions Exercise 2(a)
I.
Question 1.
When the origin is shifted to (4, -5) by the translation of axes, find the coordinates of the following points with reference to new axes.
i) (0, 3), ii) (-2, 4) iii) (4, -5)
Solution:
i) New origin = (4, -5); h = 4, k = -5
Old co-ordinates are (0, 3)
x = 0, y = 3
x’ = x – h = 0 – 4 = -4
y’=y-k = 3 + 5 = 8
New co-ordinates are (—4, 8)
ii) Old co-ordinates are (-2, 4)
x = -2, y = 4
x’ = x- h = -2 – 4 = -6
y’=y-k=4 + 5 = 9
New co-ordinates are (-6, 9)
iii) Old co-ordinates are (4, -5)
x = 4, y = -5
x’ = x – h = 4- 4 = 0
y = y – k = -5 + 5 = 0
New co-ordinates are (0,0)
Question 2.
The origin is shifted to (2, 3) by the translation of axes. If the coordinates of a point P changes as follows, find the coordinates of P in the original system.
i) (4, 5) ii) (-4, 3), iii) (0, 0)
Solution:
i) New co-ordinates are (4, 5)
x’ = 4, y’ = 5
x = x’ + h = 4 + 2 = 6
y = y’ + k = 5 + 3 = 8
Old co-ordinates are (6, 8)
ii) New co-ordinates are (-4, 3)
x’ = – 4, y’ = 3
x = x’ + h = -4 + 2 = -2
y = y’ + k = 3 + 3 = 6
Old co-ordinates are (-2, 6)
iii) New co-ordinates are (0, 0)
x’ = 0, y’ = 0
x = x’ + h = 0 + 2 = 2
y = y’ + k = 0 + 3 = 3
Old co-ordinates are (2, 3)
![]()
Question 3.
Find the, point to which the origin is to be shifted so that the point (3, 0) may change to (2, -3).
Solution:
(x, y) = (3, 0)
(x’, y’) = (2, -3)
Let (h, k) be the shifting origin.
h = x – x’= 3- 2 = 1
k = y – y’ = 0 + 3 = 3
∴ (h, k) = (1, 3)
Question 4.
When the origin is shifted to (-1, 2) by the translation of axes, find the transformed equations of the following.
i) x² + y² + 2x – 4y.+ 1 = 0
ii) 2x² + y² – 4x + 4y = 0
Solution:
i) The given equation is
x² + y² + 2x – 4y + 1 = 0
Origin is shifted to (-1, 2)
h = -1, k = 2
Equation of transformations are
x = x’ + h, y = y’ + k
i.e., x = x’ – 1, y = y’ + 2
The new equation is
(x’ – 1)² + (y’ + 2)² + 2(x’ – 1) – 4(y’ + 2) + 1 = 0
⇒ (x’)² + 1 – 2x’ + (y’)² + 4 + 4y’ + 2x’ – 2 -4y’ – 8 + 1 = 0
(x’)² + (y’)² -4 = 0
The transformed equation is x² + y² – 4 = 0
ii) Old equation is
2x² + y² – 4x + 4y = 0
New equation is 2(x’ – 1)² + (y’ + 2)² —4(x’ – 1) + 4(y’ + 2) = 0
2[(x’)² + 1 – 2x’] + (y’)² + 4 + 4y’ – 4x’ + 4 + 4y’ + 8 = 0
2(x’)² + 2 – 4x’ + (y’)² + 4 + 4y’ – 4x’ + 4 + 4y’ + 8 = 0
2(x’)² + (y’)² – 8x’ + 8y’ + 18 = 0
The transformed equation is
2x² + y² – 8x + 8y+18 = 0
Question 5.
The point to which the origin is shifted and the transformed equation are given below. Find the original equation.
i) (3,-4);x² + y² = 4
ii) (-1, 2); x² + 2y² + 16 = 0
Solution:
i) Given shifting origin = (3, – 4) = (h, k)
x’ = x – h,
= x – 3
y’ = y – k
= y + 4
The original equation of (x’)² + (y’)² = 4 is
(x – 3)² + (y + 4)2 = 4
x² – 6x + 9 + y² + 8y + 16 = 4
x² + y² – 6x + 8y + 21 =0
ii) Given shifting origin = (h, k) = (-1,2)
x’ = x – h,
= x + 1
y’ = y – k
y = y – 2
The original equation of
x’² + 2y’² + 16 = 0 is
(x + 1)² + 2(y – 2)² + 16 = 0
x² + 2x + 1 + 2y² – 8y + 8 + 16 = 0
x² + 2y² + 2x – 8y + 25 = 0
![]()
Question 6.
Find the point to which the origin is to be shifted so as to remove the first degree terms from the equation.
4x² + 9y² – 8x + 36y + 4 = 0
Solution:
The given equation is
4x² + 9y² – 8x + 36y + 4 = 0
a = 4 g = -4
b = 9 f = 18
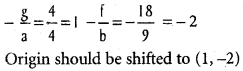
Origin should be shifted to (1, -2)
Question 7.
When the axes are rotated through an angle 30°, find the new coordinates of the following points,
i) (0, 5) ii) (-2, 4) hi) (0, 0)
Solution:
i) Given 0 = 30°
Old co-ordinates are (0, 5)
i.e., x = 0, y = 5
x‘ = x. cos θ + y. sin θ
= 0. cos 30° + 5. sin 30° = \(\frac{5}{2}\)
= – x sin θ + y cos θ
= – 0. sin 30° + 5 cos 30° =
New co-ordinates are \(\left(\frac{5}{2}, \frac{5 \sqrt{3}}{2}\right)\)
ii) Old co-ordinates are (-2, 4)
x= -2, y = 4
x’ = x cos θ + y sin θ
= (-2). cos 30°+ 4. sin 30°
= -2. \(\frac{\sqrt{3}}{2}\) + 4. \(\frac{1}{2}\) = – √3 +2
y’ = -x sin θ + y cos θ
= – (-2) sin 30° + 4 cos 30°
= 2 . \(\frac{1}{2}\) + 4. \(\frac{\sqrt{3}}{2}\)
= 1 + 2 √3
New co-ordinates are (- √3 + 2, 1 + 2√3)
iii) Given (x, y) = (0,0) and 0 = 30°
x = (0, y) ⇒ x = x’. cos 30° – y’ sin 30°
= 0. \(\frac{\sqrt{3}}{2}\) – 0. \(\frac{1}{2}\) =0
y = x’. sin 30° + y’.cos 30°
= 0.\(\frac{1}{2}\) + 0.\(\frac{\sqrt{3}}{2}\) = 0
New co-ordinates of the point are (0, 0)
Question 8.
When the axes are rotated through an angle 60°, the new co-ordinates of three points are the following
i) (3, 4) ii) (-7, 2) iii) (2, 0) Find their original coordinates.
Solution:
i) Given 0 = 60°
New co-ordinates are (3, 4)
x’ = 3, y’ = 4
x = x’ cos θ – y’ sin θ
= 3. cos 60° – 4. sin 60°
\(=3 \cdot \frac{1}{2}-\frac{4 \cdot \sqrt{3}}{2}=\frac{3-4 \sqrt{3}}{2}\)
y = x’ sin θ + y’ cos θ
= 3 sin 60° + 4. cos 60°
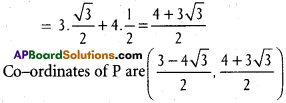
ii) New co-ordinates are (-7, 2)
x’= -7, y’ = 2
x = x’ cos θ – y’ sin θ
= (-7) cos 60° – 2. sin 60°
\(=-7 \cdot \frac{1}{2}-2 \cdot \frac{\sqrt{3}}{2}=\frac{-7-2 \sqrt{3}}{2}\)
y = x’ sin θ + y’. cos θ
= – 7. sin 60° + 2. cos 60°
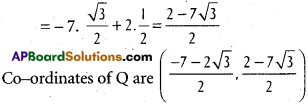
iii) New co-ordinates are (2, 0)
x’ = 2, y’ = 0
x = x’ cos θ – y’ sin θ
= 2. cos 60° – 0. sin 60°
= 2.\(\frac{1}{2}\) – 0.\(\frac{\sqrt{3}}{2}\) =1 – 0 = 1
y = x’ sin θ + y’ cos θ
= 2. sin 60° + 0. cos 60°
= 2.\(\frac{\sqrt{3}}{2}\) + 0.\(\frac{1}{2}\) = √3
Co-ordinates of R are (1, √3)
![]()
Question 9.
Find the angle through which the axes are to be rotated so as to remove the xy term in the equation.
x² + 4xy + y² – 2x + 2y – 6 = 0.
Solution:
Compare the equation
x² + 4xy + y² – 2x + 2y – 6 = 0
with ax² + 2hxy + by² + 2gx + 2fy + c = 0
a = 1, h = 2, b = 1, g = -1, f = 1, c = -6
Let ‘θ’ be the angle of rotation of axes, then
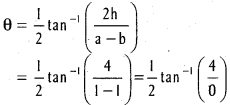
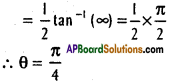
II.
Question 1.
When the origin is shifted to the point (2, 3), the transformed equation of a curve is x² + 3xy – 2y² + 17x – 7y – 11= 0. Find the original equation of the curve.
Solution:
Equations of transformation are
x = x’ + h, y = y’ + k
x’ = x – h = x – 2, y’ = y – 3
Transformed equation is
x² + 3xy – 2y² + 17x – 7y – 11 = 0
Original equation is
(x – 2)² + 3(x – 2) (y – 3) – 2(y – 3)² + 17(x – 2) – 7(y – 3) – 11 = 0
⇒ x² – 4x + 4 + 3xy – 9x – 6y + 18 – 2y² + 12y – 18 + 17x – 34 – 7y + 21 -11 = 0
⇒ x² + 3xy – 2y² + 4x – y – 20 = 0
This is the required original equation.
Question 2.
When the axes are rotated through an angle 45°, the transformed equation of acurveis 17x² – 16xy + 17y² = 225. Find the original equation of the curve.
Solution:
Angle of rotation = θ = 45
x’ = x cos θ + y sin θ = x cos 45 + y sin 45 = \(\frac{x+y}{\sqrt{2}}\)
y’ = – x sin θ + y cos θ = – x sin 45 + y cos 45 = \(\frac{-x+y}{\sqrt{2}}\)
The original equation of
17x’²- 16x’y’ + 17y’² = 225 is

⇒ 17x² + 17y² + 34xy – 16y² + 16x² + 17x² + 17y² – 34xy = 450
⇒ 50x² + 18y² = 450
∴ x² + y² = 9 is the original equation.
Question 3.
When the axes are rotated through an angle a, find the transformed equation of x cos a + y sin a = p. iMM&mmn
Solution:
The given equation is x cos α + y sin α = p
∵ The axes are rotated through an angle α
x = x’ cos α – y’ sin α
y = x’ sin α + y’ cos α
The given equation transformed to
(x’ cos α – y’ sin α) cos α +
(x’ sin α + y’ cos α) sin α = p
⇒ x’ (cos² α + sin² α) = p
⇒ x’ = p
The equation transformed to x = p
Question 4.
When the axes are rotated through an angle n/6. Find the transformed equation of x² + 2 √3xy – y² = 2a².
Solution:

⇒ 3X² – 2√3 XY + Y² + 2√3|√3X² +2XY – √3Y²|- (x² +3Y² +2√3XY) =8a²
⇒ 3X² -2V3XY +Y² +6X² + W3XY – 6Y² – X² – 3Y² – 2√3 XY = 8a²
⇒ 8X² – 8Y² = 8a² ⇒ X² – Y² = a²
The transformed equation is x² – y² = a²
![]()
Question 5.
When the axes are rotated through an angle \(\frac{\pi}{4}\), find the transformed equation of 3x² + 10xy + 3y² = 9.
Solution:
Given equation is
3x² + 10xy + 3y² – 9 = 0 ………….. (1)
Angle of rotation of axes = θ = \(\frac{\pi}{4}\)
Let (X, Y) be the new co-ordinates of (x, y)
x = X cos θ – Y sin θ
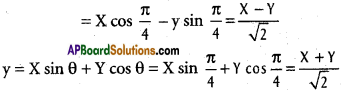
Transformed equation of (1) is
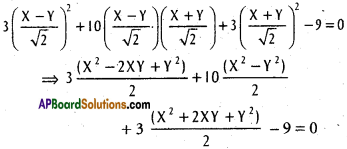
⇒ 3X² – 6XY + 3Y² + 10X² – 10Y² + 3X² + 6XY + 3Y² – 18 = 0
∴ 16X² – 4Y² -18 = 0
∴ 8X² – 2Y² = 9
∴ 8X² – 2Y² = 9
The transformed equation is 8x² – 2y² = 9