Inter 1st Year Maths 1B Locus Solutions Ex 1(a)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Locus Solutions Exercise 1(a) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B Locus Solutions Exercise 1(a)

I.

Question 1.
Find the equation of the locus of a point that is at a distance 5 from A (4, – 3).
Solution:
A (4, -3) is the given point P(x, y) is any point on the locus.

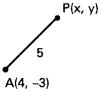
Given condition is CP = 5
CP² = 25
(x – 4)² + (y + 3)² = 25
x² – 8x + 16 + y² + 6y + 9 – 25 = 0
Equation of the locus of P is x²+ y² – 8x + 6y = 0.

Question 2.
Find the equation of locus of a point which is equidistant from the points A(-3, 2) and B(0, 4).
Solution:
A (-3, 2), B (0,4) are the given points
P (x, y) is any point on the locus

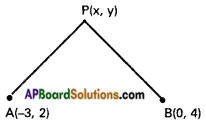
Given condition is PA = PB
PA² = PB²
(x+3)² + (y – 2)² = (x – 0)² + (y – 4)²
x² + 6x + 9 + y² – 4y + 4 = x² + y² – 8y +16
6x + 4y = 3 is the equation of the locus.

Question 3.
Find the equation of locus of a point P such that the distance of P from the origin is twice the distance of P from A (1, 2).
Solution:
O(0,0), A (1,2) are the given points
P (x, y) is any point on the locus

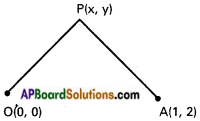
Given condition is OP = 2AP
OP² = 4 AP²
x² + y² = 4 [(x – 1)² + (y – 2)²]
= 4 (x² – 2x + 1 + y² – 4y + 4)
x² + y² = 4x² + 4y² – 8x – 16y + 20
Equation to the locus of P is
3x² + 3y² – 8x – 16y + 20 = 0.

Question 4.
Find the equation of locus of a point which is equidistant from the coordi¬nate axes.
Solution:
P(x, y) is any point on the locus.
PM and PN are perpendiculars from P on X and Y – axes.

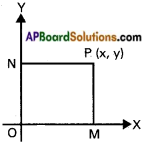
Given PM = PN ⇒ PM² = PN²
y² = x²
Locus of P is x² – y² = 0

Question 5.
Find the equation of locus of a point equidistant from A (2, 0) and the Y- axis.
Solution:
A (2,0) is the given point.
P (x, y) is any point on the locus.

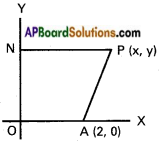
Draw PN perpendicular to Y – axis.
Given condition is PA = PN
PA² = PN²
(x – 2)² + (y – 0)² = x²
x² – 4x + 4 + y² = x²
Locus of P is y² – 4x + 4 = 0

Question 6.
Find the equation of locus of a point P, the square of whose distance from the origin is 4 times its y coordinate.

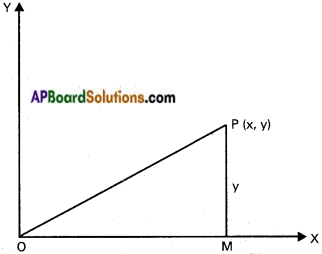
Solution:
P(x, y) is any point on the locus
Given condition is OP² = 4y ⇒ x² + y² = 4y
Equation of the locus of P is x² + y² – 4y = 0

Question 7.
Find the equation of locus of a point ‘P’ such that PA² + PB² = 2c², where A = (a, 0), B = (-a, 0) and 0 < |a| < |c|.
Solution:
Let P (x, y) be a point in locus.
A = (a, 0); B = (-a, 0)
Given condition is PA² + PB² = 2c²
(x – a)² + (y – 0)² + (x + a)² + (y – 0)² = 2c²
x² – 2ax + a² + y² + x² + 2ax + a² + y² = 2c²
2x² + 2y² = 2c² – 2a²
∴ x² + y² = c² – a² is the locus.

II.

Question 1.
Find the equation of locus of P, if the line segment joining (2, 3) and (-1, 5) subtends a right angle at P.
Solution:
A(2,3), B (-1, 5) are the given points.
P(x, y) is any point on the locus.

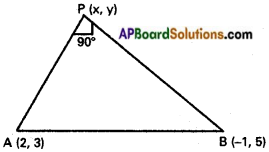
Given condition is, ∠APB = 90°
AP² + PB² = AB²
(x – 2)² + (y – 3)² + (x + 1)² + (y – 5)² = (2 + 1)² + (3 – 5)²
x² – 4x + 4 + y² – 6y + 9 + x² + 2x + 1+ y² – 10y + 25 = 9 + 4
2x² + 2y² – 2x – 16y + 26 = 0
Locus of P is x² + y² – x – 8y + 13 = 0
(x, y) ≠ (2,3) and (x, y) ≠ (-1, 5)

Question 2.
The ends of the hypotenuse of a right angled triangle are (0, 6) and (6, 0). Find the equation of locus of its third vertex.
Solution:
A(0,6), B (6,0) are the ends of the hypotenuse,
P (x, y) is the third vertex.
∴ The given condition is ∠APB = 90°

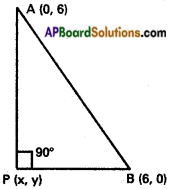
AP² + PB² = AB²
(x – 0)² + (y – 6)² + (x – 6)² + (y – 0)² = (6 – 0)² + (0 – 6)²
x² + y² – 12y + 36 + x² – 12x + 36 + y² = 36 + 36
2x² + 2y² -12x -12y = 0
Locus of P is x² + y² – 6x – 6y = 0
(x, y) ≠ (0,6) and (x, y) ≠ (6,0).

Question 3.
Find the equation of the locus of a point, the difference of whose distances from (-5, 0) and (5, 0) is 8.
Solution:
A(5,0), B(-5,0) are the given points.

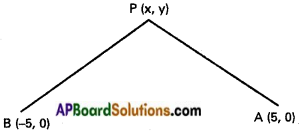
P(x, y) is any point on the locus.
Given condition is |PA – PB| = 8
PA – PB = 8 ………..(1)
PA² – PB² = [(x – 5)² + (y – 0)²] – [(x + 5)² + (y – 0)²]
= x² – 10x + 25 + y² – x² – 10x – 25 – y²
= – 20x
(PA + PB) (PA – PB) = -20x
(PA + PB) 8 = -20x
PA + PB = –\(\frac{5}{2}\)x …………..(2)
Adding (1) and (2),
2PA = –\(\frac{5x}{2}\) + 8 = \(\frac{-5 x+16}{2}\)
4PA = – 5x + 16
16PA² = (- 5x + 16)²
16 [(x – 5)² + y²] = (- 5x + 16)²
16 [x² – 10x + 25 + y²] = [- 5x + 16]²
16x² + 16y²2 – 160x + 400 = 25x² + 256 – 160x
9x² – 16y² = 144
Dividing with 144, locus of P is
\(\frac{9 x^{2}}{144}-\frac{16 y^{2}}{144}=1\) i.e., \(\frac{x^{2}}{16}-\frac{y^{2}}{9}=1\)

Question 4.
Find the equation of locus Of P, if A=(4,0), B = (- 4,0) and |PA- PB| =4.
Solution:
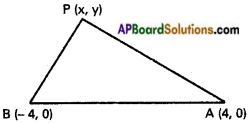
A = (4, 0), B = (-4, 0) are the given points.
P (x, y) is any point on the locus.
The given condition is |PA – PB| = 4 …………… (1)
PA² – PB²= [(x- 4)² + (y – 0)²] – [(x + 4)² + y²]
= x² – 8x+ 16 + y² – x² – 8x – 16 – y²
= -16x

(PA + PB) (PA – PB) = -16x
(PA + PB) 4 = – 16x
PA + PB = – 4x ………….. (2)
Adding (1) and (2),
2PA = 4 – 4x
PA = 2 – 2x
PA² = (2 – 2x)²
(x – 4)² + (y – 0)² = (2 – 2x)²
x² – 8x + 16 + y² = 4 + 4x² – 8x
3x² – y² = 12
Dividing with 12, locus of P is \(\frac{3 x^{2}}{12}-\frac{y^{2}}{12}=1\)
i.e., \(\frac{x^{2}}{4}-\frac{y^{2}}{13}=1\)

Question 5.
Find the equation of the locus of a point, the sum of whose distances from (0, 2) and (0, -2) is 6.
Solution:
A (0,2), B (0, -2) are the given points.

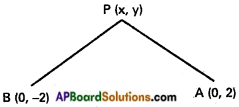
P(x, y) is any point on the locus.
Given condition is PA + PB = 6 ……….. (1)
PA² – PB² = [(x – 0)² + (y – 2)²] – [(x – 0)² + (y + 2)²]
= x² + y² – 4y + 4 – x² – y² – 4y – 4 = – 8y
(PA + PB) (PA – PB) = -8y
6(PA – PB) = – 8y
PA – PB = –\(\frac{8y}{6}\)
PA-PB = –\(\frac{4y}{3}\) ……. (2)
Adding (1) and (2), 2PA = 6 –\(\frac{4y}{3}\)

9x² + 9y² + 36 = 81 + 4y²
9x² + 5y² = 45
Dividing with 45,

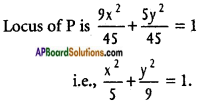
Question 6.
Find the equation (rf the locus of P, if A= (2,3), B = (2, -3) and PA + PB = 8.
Solution:
A (2, 3), B (2, -3) are the given points.

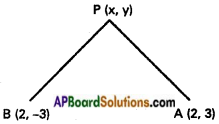
P(x, y) is any point on the locus.
Given condition is PA + PB = 8 ……….. (1)
PA² – PB² = [(x – 2)² + (y – 3)²] – [(x – 2)² + (y + 3)²]
= (x – 2)² + (y – 3)² – (x – 2)² – (y + 3)² = (y – 3)² – (y + 3)² = -12y
(PA + PB) (PA – PB) = -12y
8(PA – PB) = -12y
PA – PB = \(\frac{-12 y}{8}\)
PA – PB = \(\frac{-3 y}{2}\) ……….. (2)
Adding (1) and (2),
2PA = 8 – \(\frac{3 y}{2}\) = \(\frac{16 -3y}{2}\)
4PA = 16 – 3y
16PA² = (16 – 3y)²
16 [(x – 2)² + (y – 3)²] = (16 – 3y)²
16(x² – 4x + 4 + y² – 6y + 9) = (16 – 3y)²
16x² + 16y² – 64x – 96y + 208 = 256 + 9y² – 96y
16x² + 7y² – 64x – 48 = 0
Locus of P is 16x² + 7y² – 64x – 48 = 0.

Question 7.
A(5, 3) and B (3, -2) are two fixed points. Find the equation of the locus of P, so that the area of triangle PAB is 9.
Solution:
A(5, 3), B(3, -2) are the given points.
P(x, y) is any point on the locus.

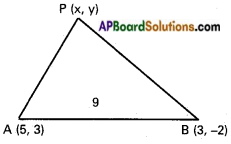
Given condition is ∆PAB = 9
\(\frac{1}{2}\)|5(-2, -y) + 3(y – 3) + x(3 + 2)|=9
|-10 – 5y + 3y – 9 + 5x| = 18
5x – 2y – 19 = ± 18
5x – 2y – 19 = 18 or 5x – 2y – 19 = – 18
5x – 2y – 37 = 0 or 5x – 2y – 1 = 0
Locus of P is (5x- 2y- 37) (5x- 2y- 1) = 0

Question 8.
Find the equation of the locus of a point, which forms a triangle of ar5a 2 with the points A(l, 1) and B (-2, 3).
Solution:
A (1, 1), B(-2, 3) are the given points.

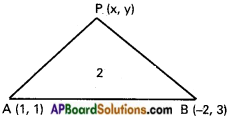
P(x, y) is any point on the locus.
Given condition is ∆PAB = 2
\(\frac{1}{2}\)|1(3 – y) – 2 (y – 1) + x (1 – 3)| = 2
|3 – y – 2y + 2 – 2x| = 4
-2x – 3y + 5 = ± 4
-2x – 3y + 5 = 4 or – 2x – 3y + 5 = – 4
2x + 3y – 1 = 0 or 2x + 3y – 9 = 0
Locus of P is (2x + 3y – 1) (2x + 3y – 9) = 0.

Question 9.
If the distance from ‘P’ to the points (2, 3) and (2, -3) are in the ratio 2 : 3, then find the equation of locus of P.
Solution:
Let P (x, y) be a point on locus.
Given points A = (2, 3), B = (2, -3)
Given condition is
PA : PB = 2 : 3
⇒ 3PA = 2PB
⇒ 9PA² = 4PB²
⇒ 9[(x – 2)² + (y – 3)²] = 4[(x – 2)² + (y + 3)²]
⇒ 9[x² – 4x + 4 + y² – 6y + 9] = 4 [x² – 4x + 4 + y² + 6y + 9]
∴ 5x² + 5y² – 20 x – 78 y + 65 = 0 is the equation of locus.

Question 10.
A (1, 2), B (2, -3) and C (-2, 3) are three points. A point ‘P’ moves such that PA² + PB² = 2PC². Show that the equation to the locus of ‘P’ is 7x – 7y + 4 = 0.
Solution:
Let P (x, y) be a point on locus.
Given points A = (1, 2), B = (2) -3) and C = (-2, 3)
Given condition is PA² + PB² = 2 PC²
⇒ (x – 1)² + (y – 2)² + (x – 2)² + (y + 3)² = 2 [(x + 2)² + (y-3)²]
⇒ 2x² + 2y² – 6x + 2y + 18 = 2x² + 2y² + 8x – 12y + 26
⇒ 14x – 14y + 8 = 0
∴ 7x – 7y + 4 = 0 is the equation of locus.

SOLVED PROBLEMS

Question 1.
Find the equation of the locus of a point which is at a distance 5 from (-2, 3) in the xoy plane.
Solution:
Let the given point be A = (-2, 3) and P(x, y) be a point on the plane.
The geometric condition to be satisfied by P to be on the locus is that
AP = 5 …………… (1)
Expressing this condition algebraically, we get
\(\sqrt{(x+2)^{2}+(y-3)^{2}}=5\)
i.e., x² + 4x + 4 + y² – 6y + 9 = 25
i.e., x² + y² + 4x – 6y – 12 = 0 ……………. (2)
Let Q(x₁, y₁) satisfy (2).

Hence AQ = 5.
This means that Q(x₁, y₁) satisfies the geometric condition (1).
∴ The required equation of locus is
x² + y² + 4x – 6y – 12 = 0.

Question 2.
Find the equation of locus of a point P, if the distance of P from A(3,0) is twice the distance of P from B(-3, 0).
Solution:
Let P(x, y) be a point on the locus. Then the geometric condition to be satisfied by P is
PA = 2PB …………. (1)
i.e., PA² = 4PB²
i.e., (x – 3)² + y² = 4 [(x + 3)² + y²]
i.e., x² – 6x + 9 + y² = 4 [x² + 6x + 9 + y²]
i.e., 3x² + 3y² + 30x + 27 = 0
i.e., x2 + y2 + lOx + 9 = 0 ………….. (2)
Let Q(x₁, y₁) satisfy (2).

∴ QA = 2QB.
This means that Q(x₁, y₁) satisfies (1).
Hence, the required equation of locus is
x² + y² + 10x + 9 = 0.

Question 3.
Find the locus of the third vertex of a right angled triangle, the ends of whose hypotenuse are (4, 0) and (0, 4).
Solution:
Let A = (4, 0) and B = (0, 4).
Let P(x, y) be a point such that PA and PB are
perpendicular. Then PA² + PB² = AB².
i.e., (x – 4)² + y² + x² + (y – 4)² = 16 + 16
i.e., 2x² + 2y² – 8x – 8y = 0
or x² + y² – 4x – 4y = 0
Let Q(x₁, y₁) satisfy (2) and Q be different from A and B.

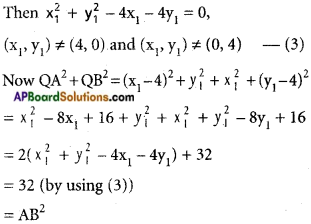
Hence QA² + QB² = AB², Q ≠ A and Q ≠ B.
This means that Q(x₁, y₁) satisfies (1).
∴ The required equation of locus is (2), which is the circle with \(\overline{\mathrm{AB}}\) as diameter, deleting the points A and B.
Though A and B satisfy equation (2), they do not satisfy the required geometric condition.

Question 4.
Find the equation of the locus of P, if the ratio of the distances from P to A(5, -4) and B(7, 6) is 2 : 3.
Solution:
Let P(x, y) be any point on the locus.
The geometric condition to be satisfied by P
is\(\frac{AP}{PB}\) = \(\frac{2}{3}\).
i.e., 3AP = 2PB ………. (1)
i.e., 9AP² = 4PB²
i.e., 9[(x – 5)² + (y + 4)²] = 4[(x – 7)² + (y – 6)²]
i.e., 9[x² + 25 – 10x + y² + 16 + 8y] = 4[x² + 49 – 14x +y² + 36 – 12y]
i.e, 5x² + 5y² – 34x + 120y + 29 = 0 ……… (2)
Let Q(x₁ y₁) satisfy (2). Then

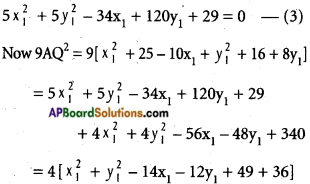
(by using (3))
– 4 [(x₁ – 7)² + (y₁ – 6)²] = 4PB²
Thus 3AQ = 2PB. This means that Q(x₁, y₁) satisfies (1).
Hence, the required equation of locus is
5(x² + y²) – 34x + 120y + 29 = 0.

Question 5.
A(2, 3) and B(-3, 4) are two given points. Find the equation of locus of P so that the area of the triangle PAB is 8.5.
Solution:
Let P(x, y) be a point on the locus.
The geometric condition to be satisfied by P is that.
area of ∆PAB = 8.5 ……….. (1)
i.e., \(\frac{1}{2}\)|x(3 – 4) + 2(4 – y) – 3(y – 3)| = 8.5
i.e., |-x + 8-2y-3y+9| = 17
i.e., |-x- 5y + 17| = 17
i.e., -x- 5y + 17 = 17 or-x-5y + 17 = -17
i.e., x + 5y = 0 or x + 5y = 34
∴ (x + 5y) (x + 5y – 34) = 0
i.e., x² + 10xy + 25y² – 34x – 170y = 0 …………. (2)
Let Q(x₁, y₁) satisfy (2). Then
x₁ + 5y₁ = 0 or x₁ + 5y₁ = 34 ………… (3)
Now, area of ∆QAB
= \(\frac{1}{2}\)|x₁(3-4) + 2(4-y₁) – 3(y₁ – 3)|
= \(\frac{1}{2}\) |-x₁ + 8 – 2y₁ – 3y₁ + 9|
= \(\frac{1}{2}\) |-x₁ – 5y₁ + 17|
= \(\frac{17}{2}\) =8.5 (by using (3))
This means that Q(x₁, y₁) satisfies (1).
Hence, the required equation of locus is
(x + 5y) (x + 5y – 34) = 0 or
x² + 10xy + 25 – y² – 34x- 170y = 0.